基于模糊隶属度中值的阈值分割算法

史露娜 兰蓉

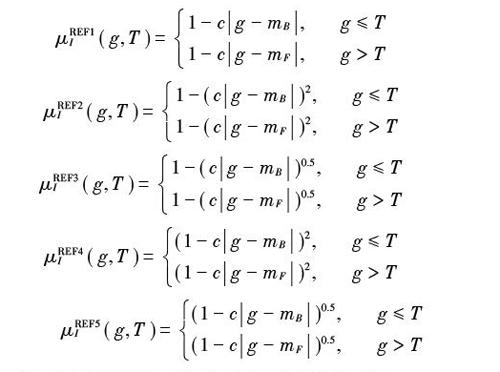
摘 要： 针对图像模糊集模型的构造问题，提出一种基于模糊隶属度中值的阈值分割算法。该算法选取有代表性的几种隶属度函数在给定灰度处的中值作为新的隶属度值，即提取多个隶属度值的一维统计特征，将灰度图像转化为一个模糊集合，再以[α]?型模糊散度为目标函数寻找最佳阈值。仿真结果显示了该算法的有效性。

关键词： 阈值分割； 隶属度函数； 模糊集； 中值； 模糊散度； 图像分割

中图分类号： TN911.73?34 文献标识码： A 文章编号： 1004?373X（2018）11?0040?06

Threshold segmentation algorithm based on median of fuzzy membership degree

SHI Luna， LAN Rong

（Xian University of Posts and Telecommunications， Xian 710061， China）

Abstract： A threshold segmentation algorithm based on median of fuzzy membership degree is proposed to construct a fuzzy set model for an image. The median （at a preset gray level） of several representative membership?degree functions is selected in the algorithm as the new membership degree value， that is， the one?dimensional statistical characteristic of multiple membership degree values is extracted to convert the gray image into a fuzzy set， and then search the optimum threshold by taking α?type fuzzy divergence as the objective function. The simulation results show that the algorithm is effective.

Keywords： threshold segmentation； membership degree function； fuzzy set； median； fuzzy divergence； image segmentation

0 引 言

图像分割是一种重要的图像处理技术，其目的是根据实际需求把图像分成具有各自特征信息的子图像，从而将感兴趣或有价值的目标提取出来，进行识别和分析[1]。它是由图像预处理到图像分析的关键步骤[2?3]。

由于具备原理简单、性能稳定的特点，基于阈值的图像分割方法成为一种最基本、应用最为广泛的分割方法，因此受到广泛关注[4?5]。阈值分割的基本原理是根据图像像素灰度值的差异性，选取一个或者多个灰度值作为阈值，对图像中的目标或区域进行分割。由于图像是对客观存在物体的一种相似性的生动模仿与描述，是对物体的一种不完全、不精确的描述。因此，模糊集理论作为处理不精确信息的有力工具，被广泛应用于图像处理领域，其中基于模糊理论及其推广概念的阈值分割算法成为研究热点之一[6?7]，也是本文的主要研究内容。

在基于模糊集理论的图像分割算法中，采用合适的方式将图像转化为对应的模糊集，即获得图像的隶属度函数是关键环节[8]。目前，研究者根据自身的偏好选择常用的图像隶属度函数，具有不可避免的主观色彩。因此，如何在现有的多种模糊隶属度函数的基础上，通过模糊信息集结的思想构造图像的模糊集模型是解决此问题的新思路[9]。

文献[9]中提出一种基于隶属度值算术平均值的分割算法（以下称其为算术平均算法）对多种信息进行均衡化处理，达到了较好的分割效果，但这种均衡始终依赖于所選的隶属度函数，隶属度值偏大或偏小也将影响该算法的分割效果。受到算数平均算子的启发，同时作为算术平均算法的一种必要补充，本文提出一种新的隶属度函数构造方法，即基于模糊隶属度中值的阈值分割算法。该方法在现有的具有代表性的几种隶属度函数基础上，选取其中值作为新的隶属度值将灰度图像转化为模糊集合，再以[α]?型模糊散度为目标函数寻找最佳阈值实现分割。因此，该算法依靠图像模糊隶属度值的中值，一种常用的一维统计特征获得图像的隶属度。由于将多种隶属度函数在给定灰度处的中值作为新的隶属度值，改善了单一隶属度函数对不同特征图像的低匹配性，同时，在一定程度上避免了算术平均算法的极端值带来的影响。

1 灰度图像的模糊集表示

所谓模糊性，是指概念或对象集存在外延不明确性，即这些集合具有“亦此亦彼”的过渡性质[10]。模糊集合突破了经典集合理论的局限，更符合客观实际。模糊集合采用隶属函数描述模糊性、不精确性信息。因此，隶属函数是表示模糊集合的基本手段，也是模糊集合应用的基础。根据对象的特点，合理地确定隶属函数成为模糊集应用的关键之一。然而，如何建立隶属函数至今仍无统一的方法可循，其确定往往具有一定的主观色彩。

1.1 模糊集

在模糊集合理论中，一般用隶属度描述模糊集合[11]，则其相关概念定义如下：

定义1：设[X]是论域，则[X]上的模糊集[A]可表示为：

[A=（x，μA（x））：x∈X]

其中，映射：

[μA：X→[0，1]]

称为模糊集[A]的隶属度函数。令[F（X）]表示[X]上的所有模糊集之集。

1.2 灰度图像的模糊集表示

在建立图像的模糊集模型时，常用的隶属度函数构造方法有以下四种。

1.2.1 Gamma型隶属度函数

Gamma型隶属度函数是由文献[12]提出的，其是在假设图像灰度分布满足Gamma分布的基础上，获得图像隶属度函数的方法。

假设T为分割阈值，则得到图像的隶属度函数为：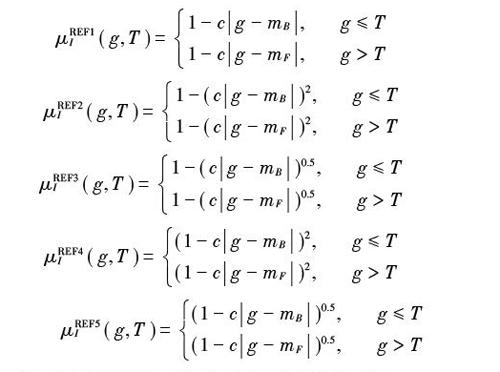

[μGammaI（g，T）=exp（-cg-mB），g≤Texp（-cg-mF），g>T]

式中：[c=1gmax-gmin]，[gmax]为图像灰度的最大值，[gmin]为图像灰度的最小值。目标与背景的均值可利用相应图像I的灰度直方图[hI]分别计算：

[mB=g=0TghI（g）g=0ThI（g）， mF=g=T+1L-1ghI（g）g=T+1L-1hI（g）]

1.2.2 限制等价函数

使用限制等价函数的概念建立图像的隶属度函数，实现图像的阈值分割，是由文献[13]提出的，并给出如下5种具体的计算公式：

[μREF1I（g，T）=1-cg-mB， g≤T1-cg-mF， g>T]

[μREF2I（g，T）=1-（cg-mB）2， g≤T1-（cg-mF）2， g>T]

[μREF3I（g，T）=1-（cg-mB）0.5， g≤T1-（cg-mF）0.5， g>T][μREF4I（g，T）=（1-cg-mB）2， g≤T（1-cg-mF）2， g>T]

[μREF5I（g，T）=（1-cg-mB）0.5， g≤T（1-cg-mF）0.5， g>T]

式中常值c的取值与[μGammaI（g，T）]中的取值一致。

1.2.3 基于对数的隶属度函数

文献[14]利用指数函数提出基于对数函数的隶属度函数，其计算公式如下：

[μexpI（g，T）=exp（-log（2）（cg-mB）2）， g≤Texp（-log（2）（cg-mF）2）， g>T]

式中常值[c]的取值与[μGammaI（g，T）]中的取值一致。

1.2.4 基于加权平均算子的隶属度函数

文献[9]中，算术平均算法采用算术平均算子，选取[n]种隶属度函数，分别为[μI1（g，T），μI2（g，T），…，μIn（g，T），]得到图像的算术平均隶属度函数如下：

[μ′I][（g，T）=1nμI1（g，T）+μI2（g，T）+…+μIn（g，T）]

2 基于中值法的隶属度函数

每一种隶属度函数都有各自的适应对象，即对某些图像能很好地提取图像特征，但对其他的图像效果却很差。因此，选取合适的构造函数得到对应的模糊集是其中最关键的步骤。

算术平均算法利用多个模糊隶属度函数构造一个新的隶属度函数，实现了信息的均衡化处理，在一定程度上避免了阈值过大或过小的问题。这种算法依赖于单一型隶属度函数的选取，隶属度值偏大或偏小会影响到该算法对图像的分割效果。为避免算术平均算法的极端值带来的不利影响，本文提出采用模糊隶属度中值获得图像的模糊隶属度函数。

设[μ1g，T，μ2g，T，…，μn（g，T）]为[n]个隶属度函数，简记为[μ1（g）， ][μ2（g），…，][ μn（g）]。先对其进行排序，简记为[μ1（g），μ2（g），…，μn（g）]，再计算它们的中值[Me（g）]，即：

[Me（g）=median{μ1（g），μ2（g），…，μn（g）}]

则，隶属度中值定义为：

[Me（g）=μi+12（g）， i为奇数μi2（g）+μi+22（g）2， i为偶数]

式中[i]表示位数，取正整数。

选取如下有代表性的5种隶属度函数[μGammaIg，T，μREF1I（g，T），μREF2I（g，T），μREF3I（g，T），][μexpI（g，T）]作為构建模糊隶属度中值法所需的隶属度函数。先对这5种隶属度函数值进行排序，依次顺序简记为：

[μ1I（g），μ2I（g），μ3I（g），μ4I（g），μ5I（g）]

然后对这5种隶属度函数在特定灰度处的隶属度值取中值：

[Me（g）=medianμ1I（g），μ2I（g），…，μ5I（g）] （1）

其中，[μ1I（g），μ2I（g），…，μ5I（g）]为相应的隶属度值。再根据：

[Me（g）=μ3I（g）] （2）

计算并得到图像灰度值[g]的隶属度函数值。

3 基于模糊隶属度中值的阈值分割算法

阈值化分割算法通过构造隶属度函数，将图像转化为一个模糊集合，需要采用目标函数优化的方法确定最佳阈值，然后通过二值化实现图像分割，将目标与背景分离。本文中目标函数采用[α]?型模糊散度公式[15]，具体计算如下所示。

定义2：设[X]为有限论域，则模糊集[A，B∈F（X）]之间的模糊散度：

[ D（A，B）=1α-1i=1n2α-1μαA（xi）（μA（xi）+μB（xi））α-1+ 2α-1（1-μA（xi））α（2-μA（xi）-μB（xi））α-1-1+ 2α-1μαB（xi）（μA（xi）+μB（xi））α-1+2α-1（1-μB（xi））α（2-μA（xi）-μB（xi））-1]

其中[α>0]且[α≠1]。

本文采用基于模糊隶属度中值的阈值分割算法，选取模糊散度[D（A，B）]作为目标函数。比较不同T时模糊散度的取值，模糊散度最小时对应的T值作为最佳阈值。[α]取经验值0.5。

下面是基于模糊隶属度中值的阈值分割算法的具体步骤：

步骤1：选择构建模糊隶属度中值法所需的隶属度函数：

[μGammaIg，T，μREF1Ig，T，μREF2Ig，T，μREF3Ig，T，μexpIg，T]

步骤2：对选取的隶属度函数在特定灰度处的隶属度值进行排序，再结合式（1）和式（2）计算得到图像灰度值[g]的隶属度函数值。

步骤3：计算[D（I，B）]，取散度最小时的[T]值为最佳分割阈值。

对于理想分割图像[B]，其隶属度函数为：

[μB（g）=1， g∈0，1，2，…，L-1]

因此，模糊散度公式可简化为：

[D（I，B）=1α-1i=1n2α-1μαI（xi）（μI（xi）+1）α-1+2α-11-μI（xi）+2α-1（μI（xi）+1）α-1-2]

则选取最佳阈值的目标函数为：

[Topt=argminTD（I，B；T）]

其中[T∈{0，1，2，…，L-1}]。

4 仿真实验

为了验证本文提出的基于模糊隶属度中值的阈值分割算法的有效性，进行了仿真实验。实验是在配置为intel core i5处理器，4 GB内存的计算机上运行的，仿真环境为Matlab。选取标准测试图像cameraman.jpg，number.tif，image1.bmp，image2.bmp， image3.bmp，image4.bmp分别进行仿真实验，比较阈值分割的效果。所选图像均为灰度图像，且均为单阈值分割。

图1～图6为选择不同隶属度函数对图像进行分割的效果对比图。

图像采用的原图如图1～图6中的图a）所示，图b）为相应原图对应的灰度直方图。图1，图2中，图c）～图i）为选择不同隶属度函数所对应的图像分割效果图；图3～图6中，图c）为理想分割图，图d）～图j）为选择不同隶属度函数所对应的图像分割效果图。

由图1可知，所有参与对比的算法均能获得较为完整的目标，图1c）与图1e）结果一致，图1d）与图1f）结果一致，都含有大量的噪声，效果不是很理想，算术平均法将部分背景像素错误地归为目标，REF3算法将少量的背景像素错误地归为目标，而本文算法能得到图1a）较为理想的分割效果。由图2c），d），e），f），h）可知，基于Gamma分布，限制等價函数REF1，REF2，指数型的对数函数及算术平均算法构造图像模糊集模型的方法完全失效，无法识别目标；图2g）显示：限制等价函数REF3算法将部分目标像素错误地归为背景；相比这些算法，本文算法能较好地分割出number原图。

图1， 图2是直观分析，图3[～]图6中由于有理想分割图，可以定量去分析，其实验结果如下所示。

在图3～图6中，将各个算法的分割图像与理想分割图像进行对比，可得每种具体算法的分割准确率[16]，其中图像分割准确率可以用来评估算法的性能，表1是7种不同算法分割效果的准确率。

在图3～图5中，将每种算法结果图与其对应的理想分割图相比较，可以看出，前6种算法不能将目标完整地分割出来，本文算法较这6种算法，完整地分割出了目标图像。再结合表1可得：针对同一幅图像的分割实验，本文算法的准确率比其他6种算法的准确率高，可验证本文算法的有效性。图6中，虽然不能直观地看出本文算法分割效果的优势，但通过表1可以看出image4图像中本文算法的分割准确率比其他算法的分割准确率高，验证了本文算法的有效性。本文算法采用隶属度函数中值法，选取有代表性的5种隶属度函数在特定灰度处的中值作为新的隶属度值，即提取多个隶属度值的一维统计特征，改善了单一隶属度函数对不同特征图像的低匹配性，同时避免了算术平均算法极端值的影响，在一定程度上改进了算术平均算法的分割效果，得到了更好的分割效果。

5 结 语

本文针对基于模糊集理论的灰度图像阈值分割算法进行研究，由于常用的图像隶属度函数均由研究者根据自身的偏好选择而来，具有不可避免的主观色彩，因此，采用模糊集理论与信息集结的思想提出基于隶属度函数中值法的阈值分割算法。该算法首先采用5种隶属度函数在给定灰度处的中值作为新的隶属度值，即提取多个隶属度值的一维统计特征，将灰度图像转化为一个模糊集合，再以[α]?型模糊散度为目标函数寻找最佳阈值，通过二值化实现图像分割。与单一型隶属度函数的算法进行对比，本文算法在一定程度上避免了主观因素的影响。与文献[9]中同样基本信息集结思想所给出的算术平均值法对比，可以看到，本文算法可以较为有效地分割出算术平均算法所不能处理的一部分图像。本文算法采用多种隶属度函数在特定灰度处的中值作为新的隶属度值，一方面改善了单一隶属度函数对不同特征图像的低匹配性，另一方面，在一定程度上避免了算术平均算法的极端值带来的影响，因此得到了较好的分割效果。

参考文献

[1] 聂方彦，高潮，郭永彩.基于新模糊准则与DE算法的红外人体图像分割[J].计算机应用研究，2010，27（4）：1594?1597.

NIE Fangyan， GAO Chao， GUO Yongcai. Infrared human image segmentation based on new fuzzy criterion and DE algorithm [J]. Computer application research， 2010， 27（4）： 1594?1597.

[2] 章毓晋.图像工程[M].北京：清华大学出版社，2013：73?74.

ZHANG Yujin. Image engineering [M]. Beijing： Tsinghua University Press， 2013： 73?74.

[3] 卢易苏，陈武凡.自动分割图像新方法研究[J].计算机应用研究，2012，29（3）：1127?1129.

LU Yisu， CHEN Wufan. A new method for automatic segmentation of images [J]. Computer application research， 2012， 29（3）： 1127?1129.

[4] 吴一全，孟天亮，吴诗婳.图像阈值分割方法研究进展20年（1994—2014）[J].数据采集与处理，2015，30（1）：1?23.

WU Yiquan， MENG Tianliang， WU Shihua. Research progress of image threshold segmentation method 20 years （1994?2014） [J]. Data acquisition and processing， 2015， 30（1）： 1?23.

[5] XU Caiyun. Review of research on image segmentation algorithm [J]. Computer knowledge & technology， 2014， 10（11）： 2637?2639.

[6] 李娟.基于模糊理论的图像分割算法研究[D].武汉：武汉科技大学，2005.

LI Juan. Research on image segmentation algorithm based on fuzzy theory [D]. Wuhan： Wuhan University of Science and Technology， 2005.

[7] 雷博，范九伦.二维广义模糊熵图像阈值分割法[J].光子学报，2010，39（10）：1907?1914.

LEI Bo， FAN Jiulun. Two?dimensional generalized fuzzy entropy image threshold segmentation method [J]. Acta photonica sinica， 2010， 39 （10）： 1907?1914.

[8] 许新征，丁世飞，史忠植，等.图像分割的新理论和新方法[J].电子学报，2010，38（z1）：76?82.

XU Xinzheng， DING Shifei， SHI Zhongzhi， et al. The new theory and method of image segmentation [J]. Acta electronica sinica， 2010， 38（S1）： 76?82.

[9] 兰蓉，沈文文.基于隶属度函数平均值的阈值分割算法[J].西安邮电大学学报，2015，20（2）：77?82.

LAN Rong， SHEN Wenwen. Threshold segmentation algorithm based on the mean value of membership function [J]. Journal of Xian University of Posts and Telecommunications， 2015， 20（2）： 77?82.

[10] ZADEH L A. Fuzzy sets [J]. Information and control， 1965， 8（3）： 338?353.

[11] BEZDEK J C. Pattern recognition with fuzzy objective function algorithms [M]. New York： Plenum Press， 1981.

[12] CHAIRA T， RAY A K. Segmentation using fuzzy divergence [J]. Pattern recognition letters， 2003， 24（12）： 1837?1844.

[13] BUSTINCE H， BARRENECHEA E， PAGOLA M. Image thresholding using restricted equivalence functions and maximizing the measures of similarity [J]. Fuzzy sets & systems， 2007， 158（5）： 496?516.

[14] PAGOLA M， LOPEZ?MOLINA C， FERNANDEZ J， et al. Interval type?2 fuzzy sets constructed from several membership functions： application to the fuzzy thresholding algorithm [J]. IEEE transactions on fuzzy systems， 2013， 21（2）： 230?244.

[15] 兰蓉，范九伦.基于[α]?型相对信息的模糊散度[J].工程数学学报，2010，27（4）：715?719.

LAN Rong， FAN Jiulun. Fuzzy divergence based on α?type relative information [J]. Journal of engineering mathematics， 2010， 27（4）： 715?719.

[16] ZHANG H， FRITTS J E， GOLDMAN S A. Image segmentation evaluation： a survey of unsupervised methods [J]. Computer vision & image understanding， 2008， 110（2）： 260?280.