基于混合蛙跳算法的半主动悬架LQG控制器设计
2018-06-12王一凡
王一凡
安徽省合肥工业大学(屯溪区) 安徽省合肥市 230041
1 引言
随着汽车工业与技术的不断发展,为更好地提升汽车的安全和舒适性,悬架系统性能也越来越得到人们的重视。由于被动悬架的刚度、阻尼不能变化,难以适应不同路况的,因而难以满保证汽车行驶过程中平顺性和操纵稳定性的要求。半主动悬架能够根据实际工况对阻尼进行调整,因此与被动悬架相较,半主动悬架在行驶过程中具有更好的使用性能[1],加之其耗能小、控制能更加迅速精确等优势,逐步成为研究热点。
对于半主动悬架控制策略,国内外都进行了广泛而深入的研究。目前,悬架的控制策略主要有:天棚阻尼控制、模糊控制、PID控制、自适应控制和最优控制等。天棚阻尼控制是通过on-off开关控制汽车悬架阻尼的控制策略,Zhang J等[2]以磁流变半主动悬架为基础,采用改进的天棚阻尼方法进行仿真实验,验证了天棚阻尼方法对操纵稳定性的提高有限。模糊控制采用语言性的控制规则,不需要系统精确数学模型,易于理解。SJ Huang等[3]提出了一种自适应模糊滑模控制器来抑制路面变化引起的簧载质量位置振荡,结果证明,有效抑制了不同路面扰动下簧载质量的振荡幅度。寇发荣等[4]对比天棚、地棚及模糊控器并进行仿真试验,结果证明模糊控制具有较好的效果。其对复杂系统的控制,但由于其模糊逻辑及推理主观性较强,难以进行推广。PID控制是Proportion、Integration、Differentiation的首字母缩写,代表了控制器的三个组成模块比例、积分和微分。Toloei A等[5]利用PID控制技术对半主动悬架进行了振动控制,系统垂直振动等均有明显的改善。但单一的PID控制对于非线性系统的调控不稳定,无法实现其动态特性。自适应控制可以根据车辆状态进行实时调整,郭孔辉等[6]提出了一种七自由度模型的自适应控制策略,应用了最优控制参数,证明自适应控制策略可以提高舒适性和安全性。但自适应控制需要实时调控,对控制系统要求较高,系统的鲁棒性易受影响。
最优控制是在给定的约束条件下,根据控制目标,对最优控制律进行设置的控制方法。其在工作过程中能够对系统内各状态变量给予全面的考虑,控制效果明显,是半主动悬架控制领域的研究热点。Chen等[7]基于电控空气悬架,提出了一种LQG控制方法,可以同时改善道路友好性和平顺性;朱龙英[8]等为克服动态系统的不确定性,采用自适应LQG控制策略,并发现其能够有效降低车身振动,显著提高了平顺性和操稳性;罗鑫源等[9]基于层次分析法(AHP)设计了一种能够降低BA、SWS和DTD的车辆主动悬架线性最优(LQG)控制器。针对控制指标的加权系数,大多采用经验试凑选取的方法,准确性较低,工作量偏大。有部分学者对此进行了研究,如陈双等[10]针对LQG控制权重系数依靠经验,具备一定的不确定性,因此采用遗传粒子群算法进行确定;张志飞等[11]使用的改进的层次分析法确定加权系数,使其准确性高于经验选取方法。但是,这些研究依然存在加权系数无法摆脱人为主观因素的影响。
本文采用最优控制作为半主动悬架系统的控制策略,并以混合蛙跳法为基础与悬架控制策略结合,确定衡量汽车平顺性的各项指标的权重系数,据此设计车辆半主动悬架的LQG控制器。在 MATLAB/Simulink 中建立1/4车辆二自由度模型进行仿真分析,验证了LQG控制器对半主动悬架调控的正确性及可行性,为半主动悬架的控制器设计拓宽了设计思路,具有一定的应用价值。
2 1/4半主动悬架模型
二自由度1/4悬架模型结构简单,又由于车身垂向振动能直观的反映汽车的行驶平顺性,该模型能直观反映出车身的垂向振动情况,因此采用1/4悬架模型,如图1所示。图中mt为非簧载质量,ms为车体质量,kt为轮胎刚度,ks为悬架弹簧刚度,c为减振器阻尼,x0为地面的扰动输入位移,x1为非簧载质量的位移,x2为车体质量的位移,F为悬架控制力。
根据牛顿第二定律,可知主动悬架的动力学方程为:
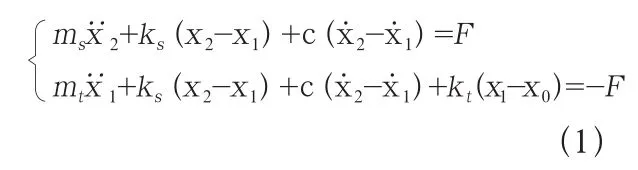
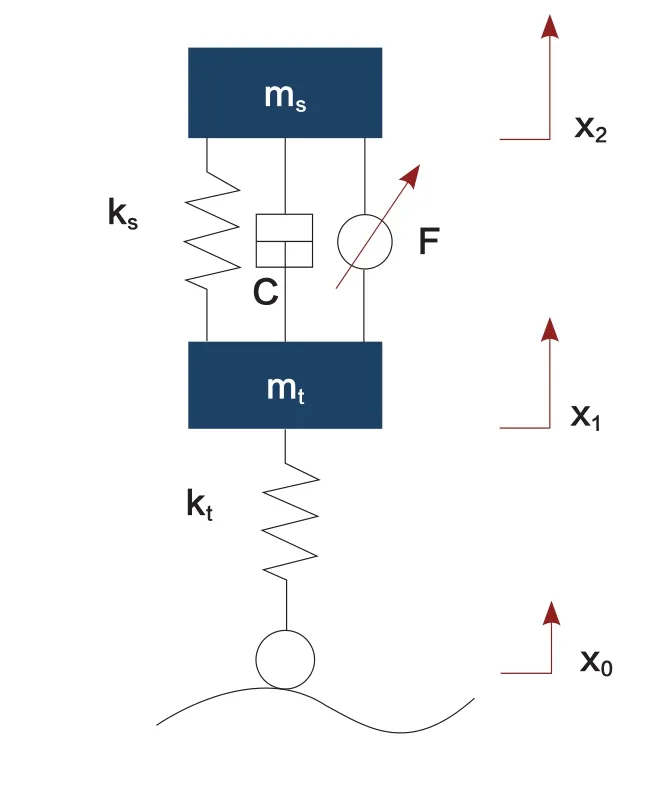
图1 1/4车辆简化模型
采用滤波白噪声的时域表达式模拟该模型的路面不平度输入,可得路面输入表达式为

式(2)中:f0为下截止频率;x0为路面不平度系数;μ为车速;w(t)为均值等于零的高斯白噪声。
二自由度1/4车模型的性能住要用车身垂向加速度、悬架动行程与轮胎动变形三个指标来衡量。则取系统的状态变量为X=[X1X2X3X4],其中X3=x2-x1,X4=x1-x0且Y(t)=X,则动力学状态方程为

其中,
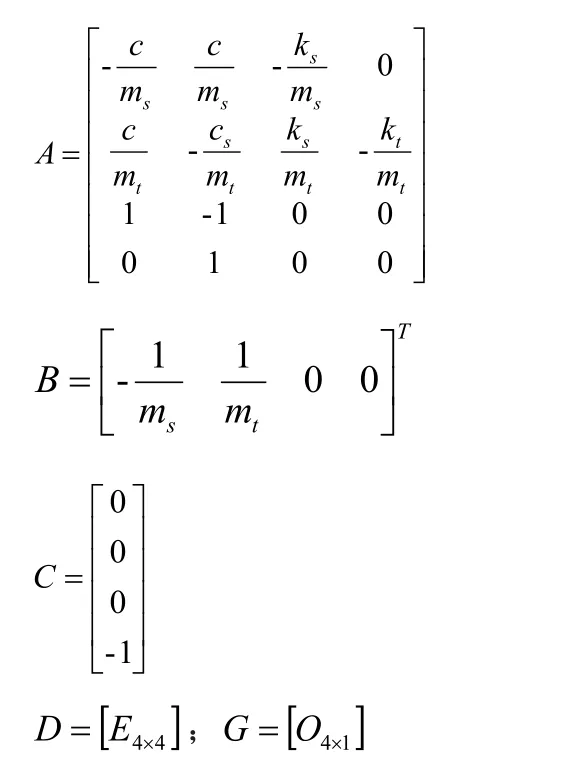
F为控制力;q=x·0(t),为路面输入矩阵。
E为单位矩阵,O为全零矩阵。
3 半主动悬架系统控制
3.1 LQG 控制器设计
根据汽车平顺性的评价标准并参考状态变量,选取控制量:
(1)车身垂向加速度:直观反映平顺性;
(2)悬架动行程:减小悬架振动并缓冲冲击;
(3)轮胎动变形:减小轮胎变形和改善接地性[12]。
根据现代控制理论,求系统的最优控制力U,使得目标函数J达到极小,从而实现最优控制[13]。
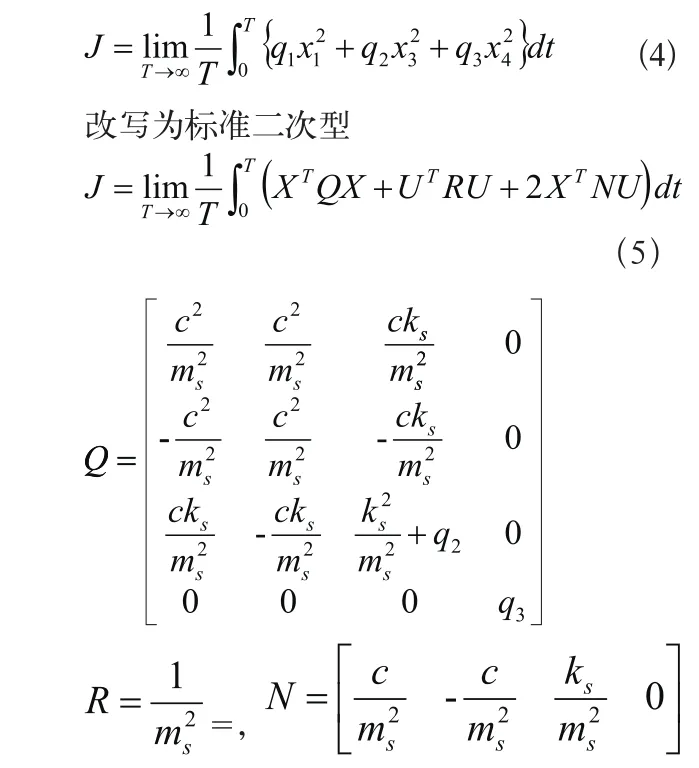
根据极值原理,可求出任意时刻最优控制力F(t):
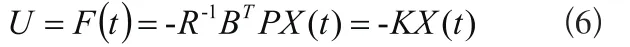
K为系统的最优反馈增益矩阵;P为常值正定矩阵。
则由黎卡提代数方程求出

在MATLAB工具箱中,调用控制函数lqr,按下式即可求出矩阵K的具体值。

3.2 采用混合蛙跳优化算法LQG设计
3.2.1 混合蛙跳优化算法
SFLA是一种受自然生物模仿启示而产生的基于群体的协同搜索方法[14]。混合蛙跳算法模拟的是在有限的空间内青蛙觅食的过程,其中湿地代表解空间,每只青蛙代表解空间中的一个解。在算法执行流程中,将青蛙被分成多个族群,其中,每个子群中具有数量相等的青蛙个体。每个子群具有不同的自身的文化,同时,每个子群内部的青蛙也具有自己的文化。首先,子群内部根据子群文化择出子群内部最优个体,所有子群搜索完成后,将所有个体混合重新划分子群。不断重复子群搜索和重新划分的过程,直至最终符合条件为止。
经典蛙跳算法局部更新策略中搜索过程的收敛过慢,所以提出了一种基于阈值选择的改进算法。改进的算法对于不满足阈值条件的个体不进行更新,个体的差异逐步减小,从而加快了算法的收敛速度,提升算法性能[15]。根据蛙跳算法建立悬架LQG控制器加权系数的优化算法,其解决问题的算法流程(如图2)包括初始化、种群划分、局部搜索和混合运算四个部分:
(1)初始化:设定种群青蛙的个数为F,族群数为m,族群内候选解个数为n,则F=m×n。
(2)族群划分:将初始种群中所有个体,按照适应度函数进行计算,根据计算结果将所有个体降序排序。排序原则是将青蛙个体与族群相互对应,第1个候选解对应第1个族群,以此类推,直至第m个候选解对应完成,当分配第m+1个候选解时,则把其再分入第个族群,其后的候选解按照此规律依次对应,直到F个青蛙全部分配完毕。
(3)局部搜索:设Pg为整个种群中适应度最好的候选解,Pb为每个子群中适应度最好的候选解,Pw为每个子群中适应度最差的候选解。对子群进行内部搜索,对子群中的Pw进行更新(如图3),更新策略如下:
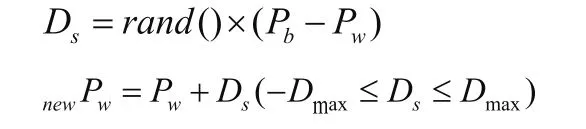
其中,Ds表示青蛙的跳动步长,产生取值为0到1之间rand()的随机数,newPw是位置更新后的Pw,Dmax是所允许最大跳动步长。
若适应度值newPw优于Pw,则newPw代替原Pw。
若适应度值Pw优于newPw,则Pg代替Pb。并进行长更新,若newPw适应度值未改进,则随机产生Pw代替Pw。
每个族群重复以上步骤,直到迭代次数满足设定的最大族群内部搜索次数。
(4)混合运算:每个族群完成内部搜索更新后,重新混合所有个体,执行族群划分和族群内部搜索,并重复进行以上过程,直到收敛到最优解或达到最大进化代数为止[16]。

图2 混合蛙跳算法流程

图3 局部搜索流程
3.2.2 适应度函数
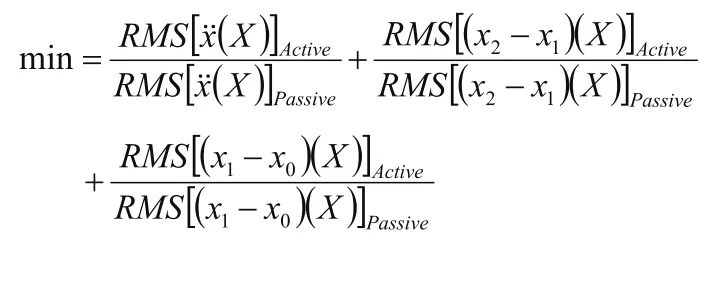
4 控制策略仿真分析
采用 MATLAB/Simulink建立车辆半主动悬架系统的仿真模型,如图4所示。选取某乘用车的悬架系统的参数为Ms=320;Mt=40;Ks=2.5×104;Kt=10×Ks;c=100 参考文献[18]在搜索 , ,范围中,经过蛙跳算法可求得满足车身垂向加速度、轮胎垂向变形量、悬架动挠度均方根值得到的车辆悬架系统各个加权系数值q1=0.45;q2=10853;q3=867。
车辆以72km/h行驶在B级路面上,采用低通滤波白噪声来模拟。下截止频率取为0.1,路面不平度系数取为1024e-6。则半主动悬架与被动悬架仿真结果及数据如下所示:
根据以上数据分析可得,相对于被动悬架,在相同结构参数和路面激励下,LQG控制器控制的半主动悬架,可以有效的减小车身垂向加速度、轮胎垂向变形量以及悬架动行程,以改善车辆的平顺性。控制器能将车身加速度均方根值由4.97m/s2降至4.17 m/s2,减幅为16.09%;悬架动行程均方根值由0.30mm将至0.28mm,减幅为6.66%;轮胎动变形均方根值由0.49mm将至0.47mm,减幅为4.08%。仿真结果表明:与被动悬架相比,半主动悬架的LQG控制器的调节作用可以有效改善车辆的平顺性,同时,对悬架的运动特性和轮胎的接地性能等不产生其他影响。
由图8分析可知,半主动悬架相较于被动悬架,车身加速度和悬架动挠度幅频特性相差不大。而轮胎动变形幅值在低频阶段,有明显降低;半主动悬架轮胎动变形低频共振和高频共振具有明显的峰值。由此看出,控制器对于半主动悬架轮胎幅频特性有较为明显的改善。
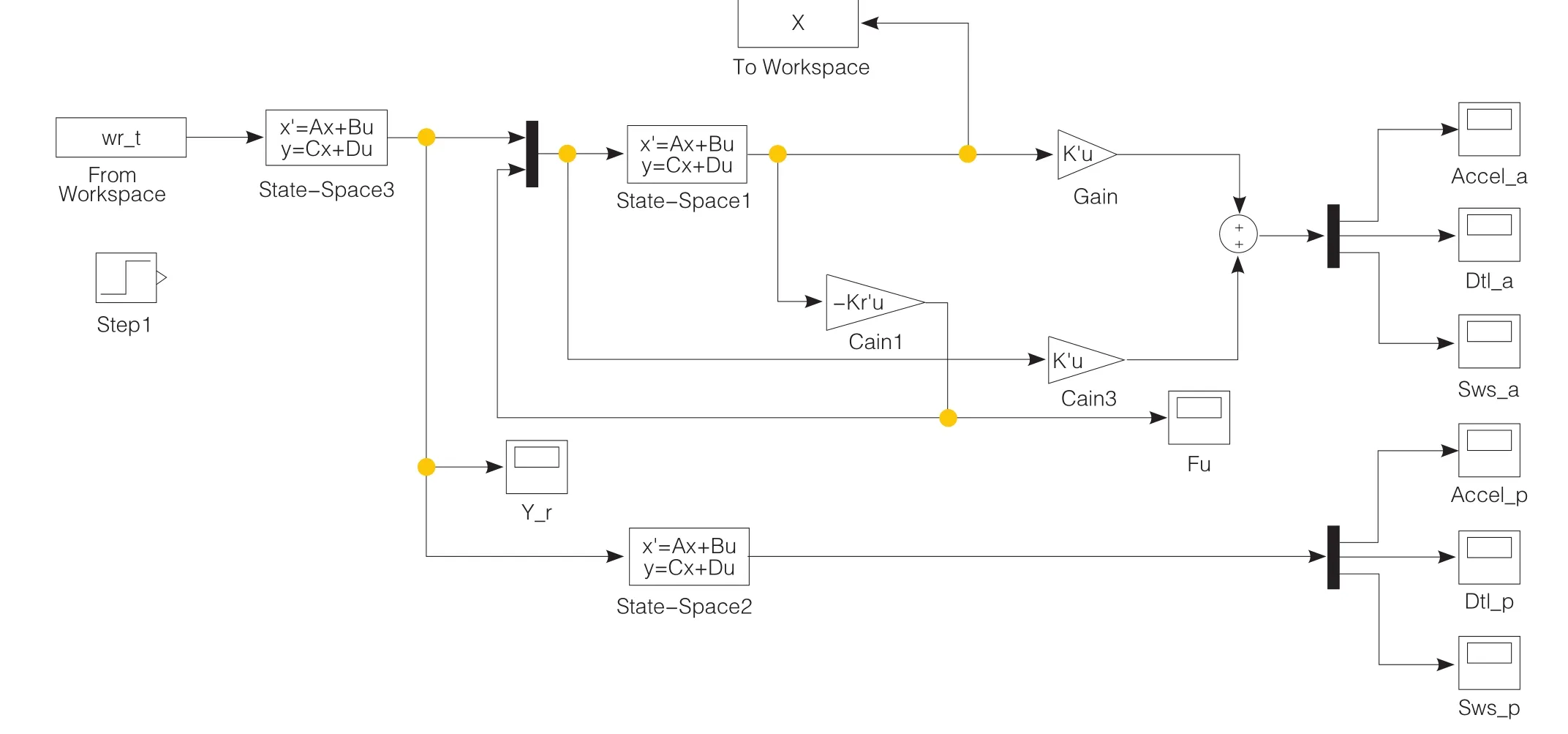
图4 半主动悬架仿真模型
图5 车身加速度曲线
图6 轮胎垂向变形量曲线

图7 悬架动扰度曲线
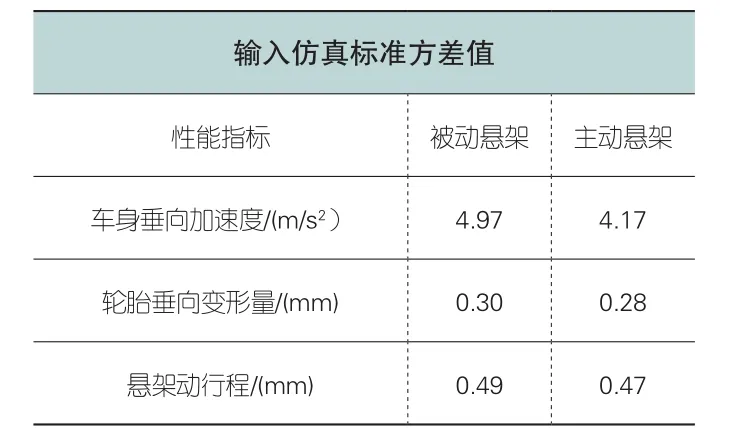
表1 被动悬架和半主动悬架性能数据对比
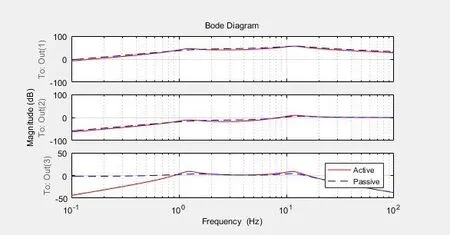
图8 BA,SWS,DTD幅频特性
综上所述,采用混合蛙跳算法确定权重系数能改善汽车平顺性各项性能指标,对车身加速度的减小有较大影响。
5 结语
通过对悬架系统的力学分析,建立了汽车1/4二自由度半主动悬架模型。采用混合蛙跳算法对半主动悬架系统的个评价指标的权重系数进行确定,为解决性能函数中权重系数不易确定的问题提供了一种算法。基于二自由度模型利用LQG对半主动悬架系统进行控制,结合路面工况进行半主动与被动悬架仿真对比分析。得出结论:与被动悬架系统相比,采用LQG控制方法的半主动悬架,其车身加速度、悬架动挠度及轮胎动变形的大小有不同程度的减小,因此,LQG控制器对提高汽车的舒适性具有较好的效果。
