基于VAR模型的安徽金融发展与经济增长分析

金欣雪，赖志花

（1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.河北地质大学 经济与贸易学院，河北 石家庄 050000）

近年来，众多学者围绕经济增长理论都进行了深入的分析，使其理论体系不断得到充实。戈德史密斯[1]在其著作《金融结构和金融发展》中选取1860-1963年间35个国家的相关数据为样本，指出影响金融发展、金融交易等的重要因素及因素间相互作用机制。麦金农与肖在其著作《经济发展中的货币与资本》[2]、《经济发展中的金融深化》[3]中，以各自角度论述了发展中国家金融发展与经济增长之间的辨证关系。圭素选取能综合代表地区差异的相关指标进行实证分析，得出与理论分析相似的结果，地区金融发展在中小企业成长力的提升方面表现良好，但在大企业方面表现欠佳。Levine等[4]对金融发展、金融结构及经济增长之间的关系从不同的角度进行了实证分析，提供了重要的方法论依据。

借鉴国外的研究成果，我国学者也做出了颇有成效的研究。韩廷春[5]通过构建关联模型，进一步提出金融发展对于经济增长作用有限。谭艳芝[6]等通过对1978-2001年的数据分析表明，金融发展对经济增长率的影响并不显著。周立[7]以1978-2000年间各地区金融发展水平和经济增长数据为样本，深入阐述了两者间的关系及有效促进机制。李强等[8]通过省级面板数据的分析发现金融发展能有效促进经济增长，但一定程度上会抑制实体经济。杨有才[9]通过建立门槛面板模型，分析发现金融发展对经济增长的正向作用只有在超过门槛值时才能得以体现。张亦春等[10]通过双门槛模型提出金融发展应与经济增长相适应。

上述学者的论证为进一步研究奠定了良好的基础，但现有研究未结合安徽省新的发展态势。本文选取安徽省1990-2015年间的金融发展和经济增长数据开展针对性的分析论证。通过建立向量自回归（vector auto-regression,VAR）动态模型，Johansen协整分析、格兰杰因果检验，实证分析了两者之间长期的动态关系，并以此为基础，建立向量误差修正(vector error correction,VEC）模型对两者之间的短期波动进行定量检验，得出短期内经济增长对金融发展有促进作用，而金融发展对经济增长的促进作用在长期内才得以体现。

1　指标的选取与数据说明

1.1　指标的选取

借鉴国内外学者对金融发展与经济发展关系研究的成果，本文研究主要包括以下实证指标。

1.1.1　金融发展指标

金融相关比率（financial interrelations ratio，FIR）。戈德史密斯1969年提出的FIR是衡量一国金融结构和金融发展的最主要指标，结合安徽省金融资产构成来看，银行信贷余额占所有金融资产的86%左右。因此，用信贷余额这个指标来代替金融资产具有较高的说服力。故本文定义金融相关比率为

其中，S、L分别代表全部金融机构存款、贷款。

保费(BF)。保险市场作为金融市场的重要组成部分，鉴于安徽保险市场发展迅速，从1995年的14.4亿元发展到了2015年的698.9亿元，将保险费用单独作为衡量金融市场的一个指标。

金融系统效率（financial system efficiency，FE）。FE=金融机构的贷款余额/金融机构的存款余额。存贷款总量反映了该地区的金融资产持有量。拥有雄厚的金融资产规模，才能更好地为当地经济建设提供支持。而金融资产使用效率与本土实体经济的发展关系密切，直接体现出本土金融的发展水平，较低的贷存比意味着较低的资产使用率和资产收益率。

1.1.2　经济增长指标

良好的经济增长可以对金融部门的发展提出更高的要求和更好的约束，为金融的平稳运行提供保障。选取人均实际国内生产总值（RGDP）为经济增长的测量指标。

1.2　数据说明

本文选取了安徽省1990-2015年的金融发展与经济增长的数据，其中反映经济增长的人均实际GDP，是以1990年为基期计算的实际值。

为了剔除通货膨胀带来的失真，在本文中，RGDP、BF为实际值，同时为了减轻数据变动幅度，本文对所有有关变量取对数值。

2　安徽金融发展与经济增长实证分析

2.1　变量的平稳性检验

对变量进行协整分析和格兰杰因果检验之前应对变量的平稳性进行检验。由表1可以得出，序列 LNRGDP、LNFIR、LNFE、LNBF 皆为不平稳序列，经过一阶差分后ADF统计量检验值分别为-3.7437、-4.3068、-5.2459、-5.0664，明显小于各显著性水平下的临界值，即所有变量的一阶差分序列均平稳，可进行协整检验。

2.2　变量间的VAR模型检验

根据AIC和SC取值最小准则，建立最优滞后期为3阶VAR模型。建立LNRGDP、LNFIR、LNFE、LNBF 的 VAR(3)模型，由 VAR(3)的检验结果可知，VAR(3)模型中R2、和F统计值分别为0.999716、0.999033、1464.973，具有统计上的显著性，说明这四个方程的效果较好。同时决定性残差协方差、AIC、SC值分别为 1.99E-13、-17.24181、-14.66962，都说明 VAR(3)模型的整体效果较好，且残差无自相关，服从正态分布，表明VAR模型的设定和滞后期数的选择是合适的。VAR(3)模型写成向量矩阵形式如下式所示。

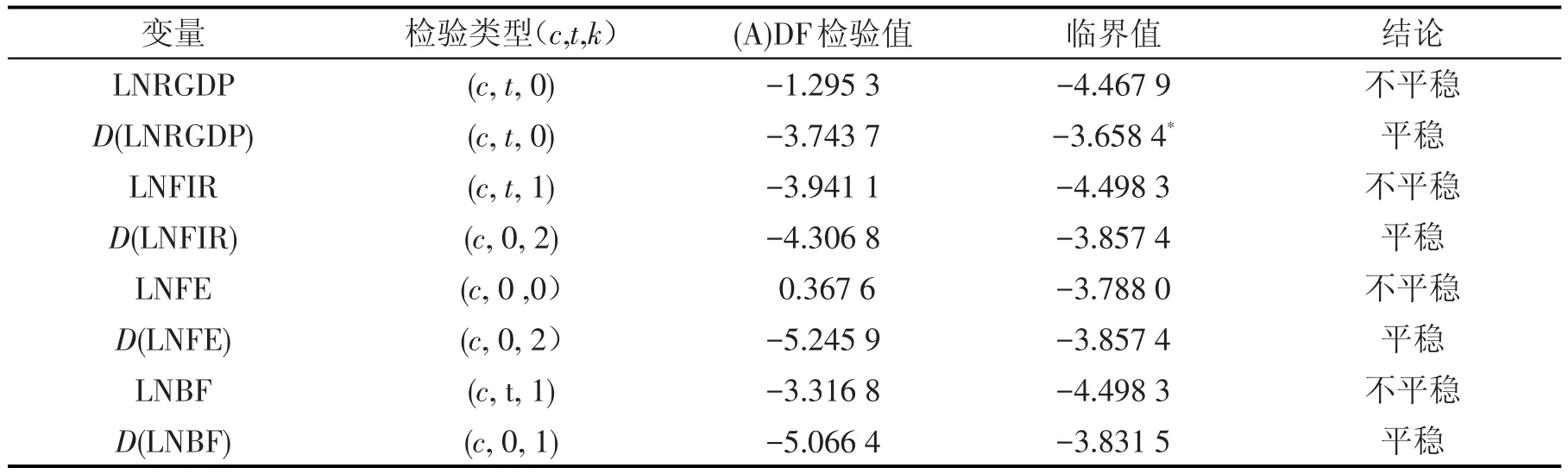
表1　变量的平稳性检验结果

可以看出，前两期人均GDP与当期人均GDPt-3呈正向变动，代表经济运行有一定程度的惯性作用。人均GDP与FIR在短期内可能会出现负的相关关系，但从长期看两者存在不一致运动的特征，通过值可以看出两者间正相关的关系是明显的。归因于安徽具有规模型金融结构特征，不仅体现为纵向金融机构布局上的规模扩张，还表现在金融机构存贷款相对于GDP的比例不断上升。

短期内金融效率（存款转换率）的提高与人均GDP为正相关的关系，人均GDP的提高在短期内对金融系统效率没有明显的促进作用，甚至为负的作用，但对金融系统效率在长期内具有正向作用，说明从长期来看，两者相互促进。金融效率的提高促进了产业结构优化，有利于实质资本的形成，促进经济增长。

还可看出保险市场的发展在长期与人均GDP为正相关的关系，人均GDP的提高对保险市场的发展也有明显促进作用。经济增长促使保险市场不断发展壮大，而保险市场为企业提供有效保证，促进了商业的发展，反过来推动了经济的发展。

2.3　变量间的Johanson协整检验

采用Johansen协整检验法，对回归系数进行整体检验。选取滞后期为2，结果：RGDP与金融发展之间存在一个协整关系（显著性水平5%），代表安徽RGDP和金融发展间存在长期相关关系。对应的长期方程为：

最大似然值为：140.0317（括号中为标准差）。

从长期来看，金融相关比率与人均GDP表现为负相关，即随着金融相关比率提高1%，人均GDP则相应会降低0.83%；而保险市场的发展以及金融系统效率与人均GDP间呈现正相关，即金融系统效率增长1%，人均GDP增长1.05%，保费增长1%，人均GDP则增长0.18%。

2.4　变量间的向量误差修正模型

由于变量之间具有协整关系，因此可建立VEC模型对短期波动进行描述，在进行该检验之前将各个变量变为一阶平稳的。从VEC模型中可以看出：四个方程的误差修正项系数都为负，说明人均生产总值与金融变量短期内对长期趋势的偏离中有21%得到纠正。VEC模型如下：

VEC模型对以上变量在短期内的相关关系进行了描述。负值的误差修正项系数，代表经济增长与金融变量之间短期内对长期趋势的偏离得到了纠正，误差修正项的值也代表模型合理。

2.5　格兰杰因果关系检验

借助格兰杰因果检验判断其因果关系，具体检验结果如表3（滞后期为2）。由此可以判断FIR和FE都拒绝不是RGDP的格兰杰原因，即金融相关比率和金融系统效率有可能是经济增长的格兰杰原因；而RGDP并非FIR和FE的格兰杰原因；BF不是RGDP的格兰杰原因，而RGDP拒绝不是BF的格兰杰原因，即RGDP可能是BF增长的格兰杰原因。

3　小结与原因分析

协整检验的结果表明，FIR与人均GDP在长期内呈反向变动，但金融系统效率、保险市场的发展与人均GDP呈正向变动。FIR和FE都拒绝不是RGDP的格兰杰原因，即有可能为RGDP的格兰杰原因；而BF不是RGDP的格兰杰原因。

通过构建VAR(3)模型得出安徽中短期内信贷规模的扩大对经济增长有着正面促进作用，投资助力拉动经济增长，长期则呈现负向变动。金融机构规模扩张对经济增长产生了负面影响，主要归因于货币政策的逆向操作，信贷投向忽视了对中小企业的支持，将难以提升产业结构、培育新的经济增长点，经济的可持续发展缺乏必要保证。

表3　人均GDP与金融发展变量的格兰杰因果检验

金融系统效率的提高对经济增长具有明显的促进作用。金融系统效率提高减轻了小企业的资金约束，促进了大量技术创新型小企业的发展，有利于增加企业数目，而金融结构优化促进了产业结构优化。

RGDP与BF之间的相互作用短期来看，经济增长能促进保费增长，保险市场的发展长期来看与经济增长呈正向变动。经济的短期增长通过参保范围的扩大，使保险密度得以提升，而伴随保险市场发展，第三产业的占比升高，推动经济发展。