数字PID控制在天线伺服系统中的应用
2018-06-11田建涛
田建涛
(中国电子科技集团公司第三十九研究所,陕西 西安 710065)
天线伺服系统是测角系统的重要组成部分,它接收来自接收机的误差信号,经过处理后驱动伺服电机,带动天线向误差减少的方向运动,并使之达到系统要求的跟踪性能和跟踪精度,从而实现对目标的快速捕获和稳定跟踪[1,2]。结合天线工作时的运动特点,并从实用性、经济性、简易性、可靠性等方面综合考虑,采用工程中广泛应用的PID(Proportional-Integral-Derivative)控制作为天线伺服系统控制方法较为合适。
1 控制原理及方法
1.1 天线伺服系统工作原理
本文研究对象为某4.5米AZ-EL-TIL座架抛物面天线。天线伺服系统在控制结构上采用典型的位置环、速度环、电流环三环控制结构,工作原理框图如图1所示[3]。其中,AZ(Azimuth)表示方位角,EL(Elevation)表示俯仰角,TIL(Tilt)表示倾斜角,AZ和EL是两个彼此相对独立的控制环路。

图1 天线控制系统工作原理框图
天线在跟踪过程中根据误差电压来调整天线运动状态,跟踪工作要求天线伺服系统应有较好的动态性能、较高的跟踪精度和较优的鲁棒性。因此,通常采用双电机消隙来消除齿轮传动中启动和反向时存在的齿隙非线性。此外,在天线运动过程中,由于两台电机的负载、扰动和实际参数及特性不完全一致,易导致两台电机出现速度同步误差。因此,通常采用“和速控制”和“差速抑制”来实现双电机同步控制。
1.2 数字式PID控制
PID控制是比例、积分和微分控制的简称,通过对被控对象的输入与输出比较误差进行比例、积分、微分计算,从而得出控制量的一种控制方法[4]。
PID控制规律可由下式表示:

(1)式中,
e(t)为给定值与控制量的偏差;
Kp为比例系数;
TI为积分时间常数;
TD为微分时间常数。
要在计算机系统中实现天线伺服控制PID控制算法,必须把PID控制算法数字化[5]。将式(1)离散化,可得离散PID控制器表达式[6]:

式中,
e(k)为k时刻给定值与控制量的偏差;
T为采样周期。
(2)式可改写可得位置型PID算式:

通常采样周期T为恒定值,一旦确定了Kp、KI、KD值,则只需计算e(k)、e(k-1)、e(k-2)即可由式(6)求出x(k)。求出x(k)后,为防止x(k)过大对系统造成不良影响,往往需要限制x(k)的取值范围。数字PID算法流程图如图2所示,可按照流程图编写PID控制算法程序。
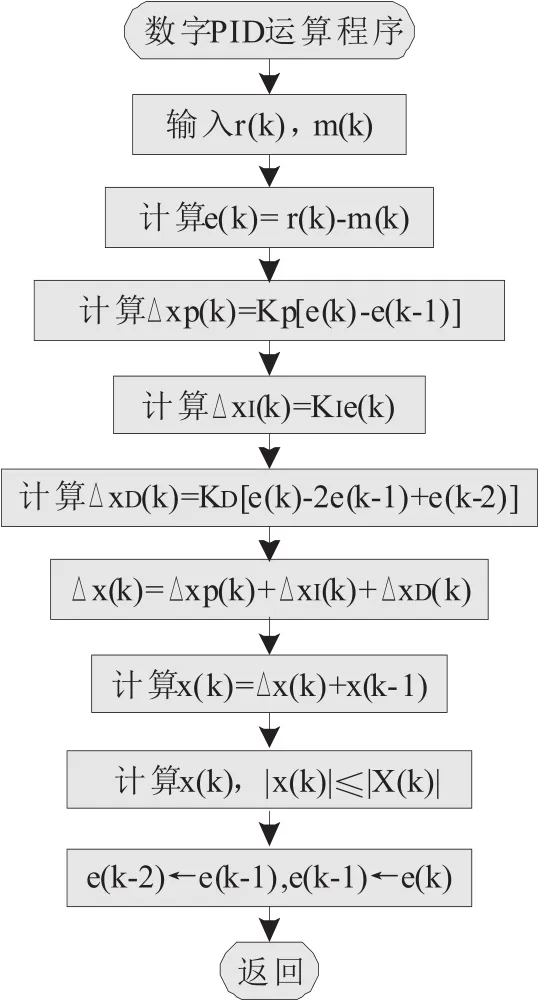
图2 数字PID算法流程图
2 位置环PID控制参数整定
在天线伺服系统中,电流环控制由伺服电机数字驱动器内部完成,PID控制应用于方位轴、俯仰轴各自的位置环、速度环。位置环是保证跟踪性能的外环,直接反应控制系统的性能指标,其输入是给定的位置角度,反馈信号来自轴角位置编码器给出的天线实时位置角度信息。下面以方位轴位置环为例,简述天线伺服系统中PID参数的整定方法。
2.1 PID控制参数整定方法选取
PID控制参数整定是指确定PID控制算法中比例度KP、积分系数KI、微分系数KD的具体取值[8]。PID控制参数整定方法主要有:理论整定法、经验公式(Z-N)法、临界比例带法、衰减曲线法和现场试凑法[9]。
理论整定法需要建立天线伺服系统的数学模型,通过理论计算来确定PID参数。由于系统模型、理想状态和参数与工程实际情况往往不完全一致,理论计算结果还需通过现场拼凑法进行完善[10,11],加之本文所述4.5米抛物面天线已有多套与之类似且能正常工作的产品作为参考,本文采用现场拼凑法进行PID参数整定。试凑法根据过渡过程的变化情况来进行PID参数整定,只需多次试凑,无需要建立复杂的控制系统数学模型,在工程实践中易操作,实用性极强。
2.2 过渡过程测试
工程上通常把从被控量的开始状态到进入目标稳态值±5%的偏差范围内且不再越出的这段过程称为过渡过程[11]。为获取合适的PID参数,测试过程如下所述:
1)采用纯比例控制(KI= 0,KD= 0,即P控制),依次增大Kp值直到不满足系统设计要求,测试并观察每组过渡过程曲线,若有满足设计要求的PID参数,记录对应Kp值并作为参数整定结果,若无,记录过渡过程曲线响应快、超调量小时对应的Kp值作为基准参数Kp0。
2)计算基准参数Kp0值对应的0.8倍和0.65倍的Kp0值,即0.8Kp0和0.65Kp0,并令Kp1=0.8Kp0、Kp2=0.65Kp0。显然,这三组值可从大到小排列为Kp0、Kp1、Kp2,依次采用PI控制(KD= 0),测试并观察每组PI参数下KI依次增大直到不满足系统设计要求时对应过渡过程曲线,若有满足设计要求的PID参数,记录对应PI参数并作为参数整定结果,若无,记录过渡过程曲线响应快、超调量小、静态误差小时对应的Kp、KI值作为基准参数KP0'、KI0。
3)计算基准参数KI0值对应的0.8倍和0.65倍的KI0值,即0.8KI0和0.65KI0,并令KI1=0.8KI0、KI2=0.65KI0。显然,这三组值可从大到小排列为KI0、KI1、KI2,依次采用PID控制,测试并观察每组PID参数下KI依次增大直到不满足系统设计要求时对应过渡过程曲线,若有满足设计要求的PID参数,记录对应PID参数并作为参数整定结果,若无返回(1)中,重新选取基准参数Kp1,重复步骤(2)和(3),直到获取满足设计要求的PID参数。
4)获取满足设计要求的PID参数后,将EL轴置于约5°、45°、90°角度,将AZ置于不同角度,正反方向多次进行过渡过程测试,对获取的PID参数进行验证,若通过验证即可作为整定结果应用,若未通过则返回对应步骤继续测试。
按照上述测试方法,以0.2°阶跃响应曲线作为过渡过程曲线,对某4.5米天线AZ轴位置环PID参数进行整定。测试过程进行到第二步即可获取到满足系统要求的PID参数,将获取的PID参数在不同角度进行测试验证,验证后所获取PID参数满足系统要求,作为最终整定结果应用。此外,众多工程实践表明,一般情况下,天线伺服系统位置环采用PI控制器就能获得满足工程需要的控制效果。
PID参数整定完成后获取的AZ轴位置环过渡过程曲线如图3所示;整定过程中部分过渡过程测试曲线图如图4、图5所示,其中,图4(a)~(d)为Kp值依次增大过渡过程曲线变化情况;图5(a)~(d)为KI值依次增大过渡过程曲线变化情况。

图3 AZ轴位置环过渡过程曲线

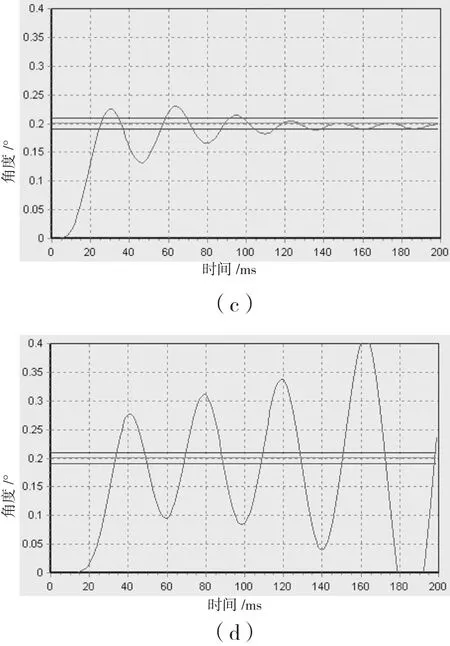
图4 Kp值依次增大过渡过程曲线图


图5 KI值依次增大过渡过程曲线图
2.3 控制参数对过渡过程曲线的影响
比例作用以偏差的Kp倍进行调节,作用效果非常明显。图4显示,增加Kp可使系统调整速度加快,上升时间缩短,伺服带宽提高,超调量增大,振荡次数增加,稳定性变差,静态误差减小,但无法消除静态误差,随着Kp进一步加大,系统变的不稳定。
积分作用对系统偏差进行积分,只要系统存在偏差,随着时间积累,积分项就会不断增加,即使是很小的误差,积分项也会随时间而慢慢增大,使得稳态误差不断减小。图5结果显示,积分作用主要用于消除静态误差,但增加KI会使系统超调量增加,振荡加剧,稳定性降低,随着KI进一步加大,系统变的不稳定。
3 结论
本文在工程实践的基础上,通过分析、试验和测试,对数字PID控制在天线伺服系统中的应用进行了探究,得出了以下结论:
1)天线伺服系统采用典型的电流环、速度环和位置环三环控制结构,采用双电机消除齿轮啮合间隙,通过“和速控制”和“差速抑制”解决双电机同步问题。
2)在计算机系统中用编程实现天线伺服控制PID控制算法,必须把PID控制算法数字化,文中给出了天线伺服控制数字PID算法编程依据。
3)给出了一种PID参数现场试凑整定方法,并应用该方法对某4.5米天线进行了PID参数整定,整定结果能够满足使用要求。
4)通常天线伺服系统位置环采用PI控制器就能获得满足工程需要的控制效果。基于过渡过程曲线实测结果,总结出了PI参数对天线过渡过程的影响情况,对天线伺服系统PID参数的整定具有实践指导意义。
[1] 李鹏. 天线伺服控制算法研究[D].大连:大连理工大学,2013.
[2] 张东云. 跟踪雷达天线伺服系统研究[D].兰州:兰州交通大学, 2013.
[3] 李莉. 双电机驱动伺服系统消隙及同步控制方法[D].天津:天津工业大学, 2017.
[4] 胡晓璐. 双电机驱动系统消隙技术研究与实现[D].西安:西安电子科技大学, 2012.
[5] Gou X. G. & Y. Z. Wu. RBF Neural Network-based PID Controller Design for the Airborne Satellite Antenna Servo System[A] // Proceedings of 2016 IEEE/CSAA International Conference on Aircraft Utility Systems(AUS)[C]. 2016:4.
[6] 杨文清. 双电机消隙伺服系统的研究与应用[D].西安:西安电子科技大学,2010.
[7] 赵景波. MATLAB控制系统仿真与设计[M].北京:机械工业出版社,2010:252-256.
[8] 段力学. PID参数整定方法分类与概述[J]. 现代计算机(专业版),2012,(7):23-26.
[9] Wu J. & M. Zhou. Digital PID Controller Designed and Realized based on State Machine[A] //IEEE Beijing Section、Global Union Academy of Science and Technology、Chongqing Global Union Academy of Science and Technology Proceedings of 2016 [C]. 2016:5.
[10]刘玲玲. PID参数整定技术的研究及应用[D].郑州:郑州大学,2010.
[11]朱嵘涛,武洪涛. 基于增量式PID算法的直流电机调速系统[J]. 仪表技术与传感器,2017,(7):121-126.
