Rogue Waves for a(2+1)-Dimensional Coupled Nonlinear Schrödinger System with Variable Coefficients in a Graded-Index Waveguide∗

Zhong Du(杜仲),Bo Tian(田播), Xiao-Yu Wu(武晓昱),and Yu-Qiang Yuan(袁玉强)

State Key Laboratory of Information Photonics and Optical Communications,and School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

1 Introduction

Rogue waves,which occur without any harbinger and disappear without any trace,have been first observed in the ocean.[1−6]The same as solitons,[7−8]rogue waves in such fields as nonlinear optics,plasma physics,laser plasma dynamics and Bose-Einstein condensation have also been studied.[9−18]In the optical fields,experimental and theoretical investigations have been made to study the rogue waves in the photonic crystal fibers,partially mode-locked fiber lasers, fiber Raman amplifiers,and whispering-gallery-mode resonators.[19−21]Work of explaining the rogue-wave phenomena via the nonlinear process has been performed.[22−23]The nonlinear Schrödinger(NLS)equation has been used to model the dynamics of the rogue waves.[12]When the inhomogeneous effects are involved,NLS equations with variable coefficients have been claimed to be more precise than their constant-coefficient versions.[23−24]Wave propagation in the graded-index nonlinear waveguides has been described by the coupled NLS systems with variable coefficients.[23]

Of interest, people have investigated a (2+1)-dimensional coupled NLS system with variable coefficients for the propagation of an optical beam inside the two-dimensional graded-index nonlinear waveguide amplifier with the polarization effects:[25−28]

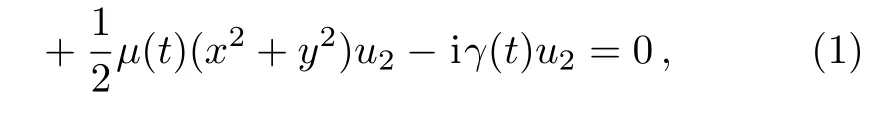
where u1(x,y,t)and u2(x,y,t)denote the two orthogonal components of the electric field,the retarded time t and transverse variables x and y are respectively normalized byand W0,the wave number k0=2πn0/λ at the input wavelength λ,the diffraction length LD=k0W02,the input beam width unit W0=(/n0)−1/4,the refractive index n=n0+n1µ(t)(x2+y2)+n2χ(t)I(x,y,t),n0and n1describe the linear contribution to the refractive index,n2is a Kerr parameter,I(x,y,t)is the optical intensity of the electric field, β(t), χ(t), µ(t)and γ(t)represent the diffraction,nonlinearity,tapering and gain/loss parameters,respectively,∆⊥= ∂2x+∂2yis the Laplacian.For System(1),combined Akhmediev breather and Kuznetsov-Ma solitons have been derived;[25]vector Hermite-Gaussian spatial solitons have been obtained;[26]vector Peregrine soliton solutions and bright-dark-soliton-rogue-wave solutions have been obtained via the similarity transformation;[27]bright soliton solutions have been constructed via the similarity transformation.[28]

Our aim in this paper will be to obtain two types of the new rogue-wave solutions for System(1),named the Type-I and Type-II rogue-wave solutions,which are different from the rogue-wave solutions in Ref.[27].In Sec.2 of this paper,via the similarity transformation,[29]we will construct the Type-I and Type-II rogue-wave solutions for System(1).In Sec.3,we will graphically study the periodic and composite rogue waves for System(1)based on the discussion of the two types of rogue-wave solutions.Our conclusions will be presented in Sec.4.

2 Rogue-Wave Solutions for System(1)

Under the similarity transformation[27]

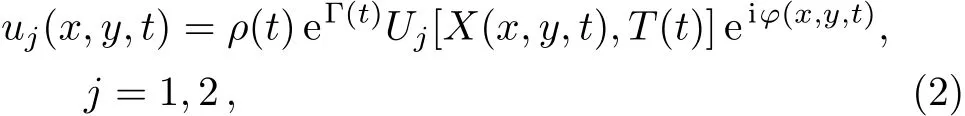
with

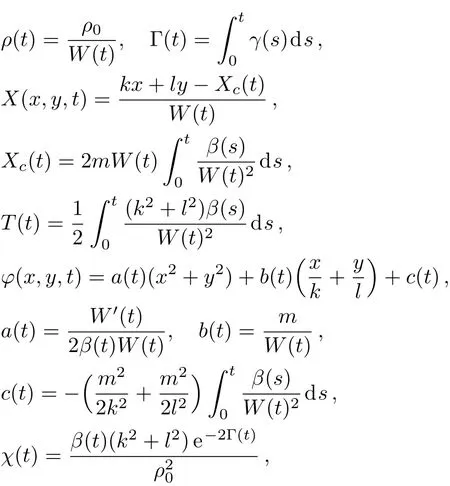
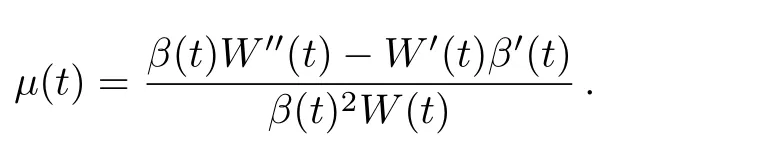
System(1)can be transformed into the coupled NLS equations[27]

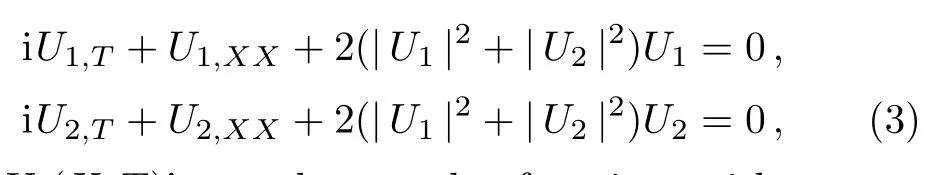
where Uj(X,T)’s are the complex functions with respect to X and T,X(x,y,t)and T(t)denote the similarity variables,W(t)and Xc(t)are the dimensionless beam width and position of the self-similar wave center,“′” represents the derivative with respect to t,ρ0,k,l,and m are the real constants,repectively.When χ(t)and β(t)satisfy the restrained condition χ(t)=[β(t)(k2+l2)e−2Γ(t)]/ρ20,the solutions for System(1)can be obtained from the solutions of Eqs.(3).

Based on Transformation(2),we have the relation between the rogue-wave solutions ujfor System(1)and Ujfor Eqs.(3)as

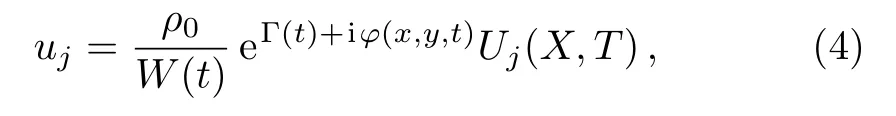
where the Type-I and Type-II rogue-wave solutions Uj(X,T)’s for Eqs.(3)have been derived.[22,30]

Substituting the rogue-wave solutions for Eqs.(3)in Refs.[22,30],i.e.,Uj’s,into Expression(4),we obtain Type-I rogue-wave solutions for System(1)as

wherec1,c2= ±2α,d2,and p are the real constants.Similarly,Type-II rogue-wave solutions for System(1)appear as

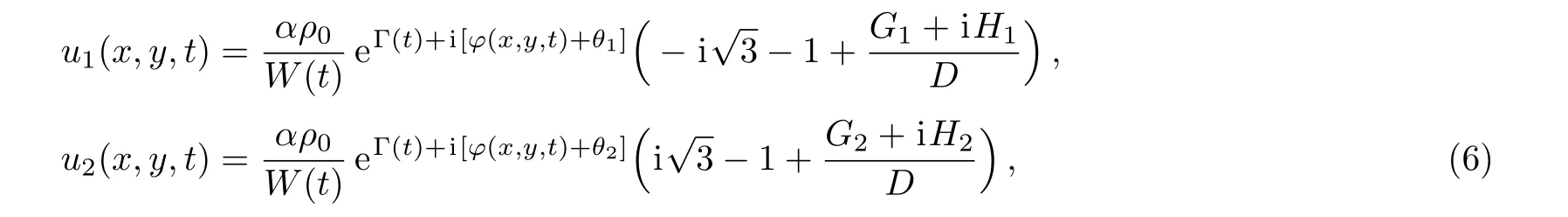
with

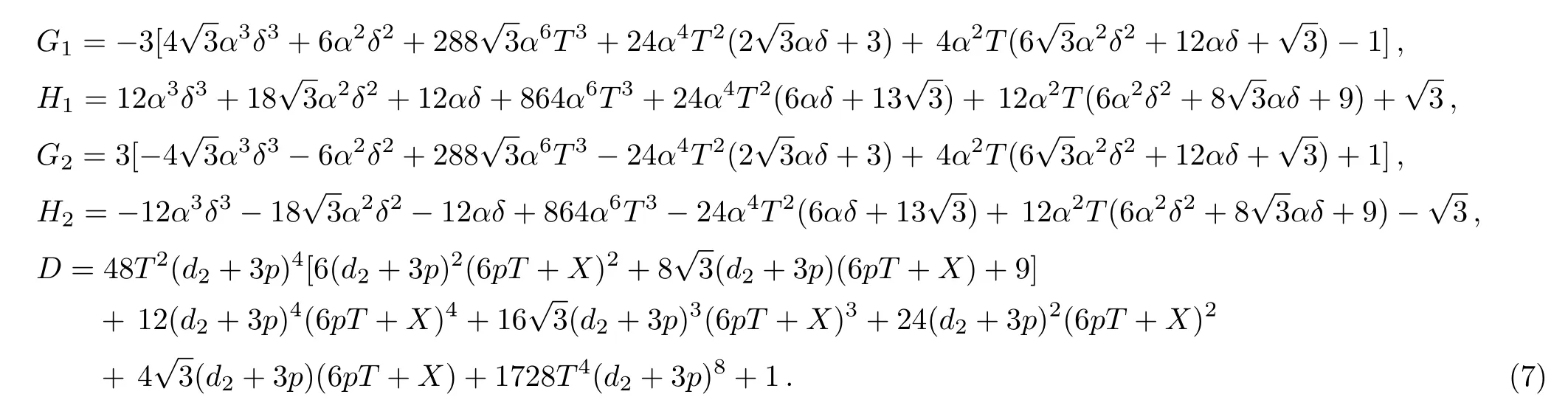
The above Type-I and Type-II rogue-wave solutions for System(1),i.e.,Solutions(5)and(6),are different from those in Ref.[27].As shown in Fig.1,Type-I rogue waves have one large crest,while Type-II rogue waves have one largest crest and two subcrests,which can be seen in Fig.2.

Fig.1 Type-I rogue wave via Solutions(5)with k=l=2,ρ0=m=1,p=0.01,d2=0.5,β(t)=0.5,W(t)=1,γ(t)=0,(a),(b)y=0,(c),(d)x=0.

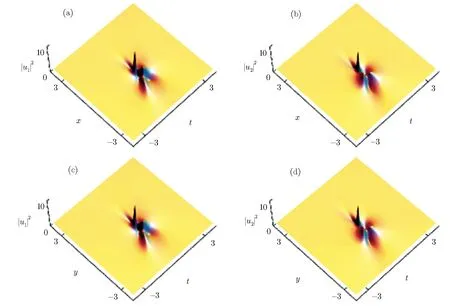
Fig.2 Type-II rogue wave via Solutions(6)with the same parameters as those in Fig.1.

3 Discussions on the Rogue Waves for System(1)

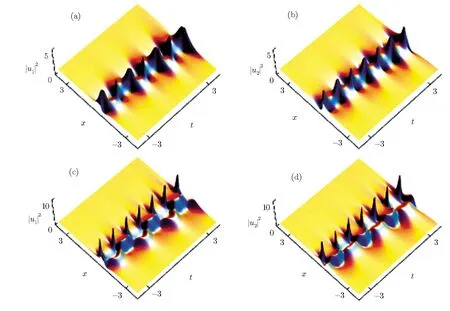
Fig.3 Type-I rogue wave via Solutions(5)with k=l=2,ρ0=m=1,p=0.01,d2=0.5,y=0,β(t)= β0eγ0tcos(σt),W(t)=er0t/2,γ(t)= γ0/2,β0=0.5,γ0=0.15,σ =2.5;(c),(d)Type-II rogue wave via Solutions(6)with the same parameters as those in Fig.1.

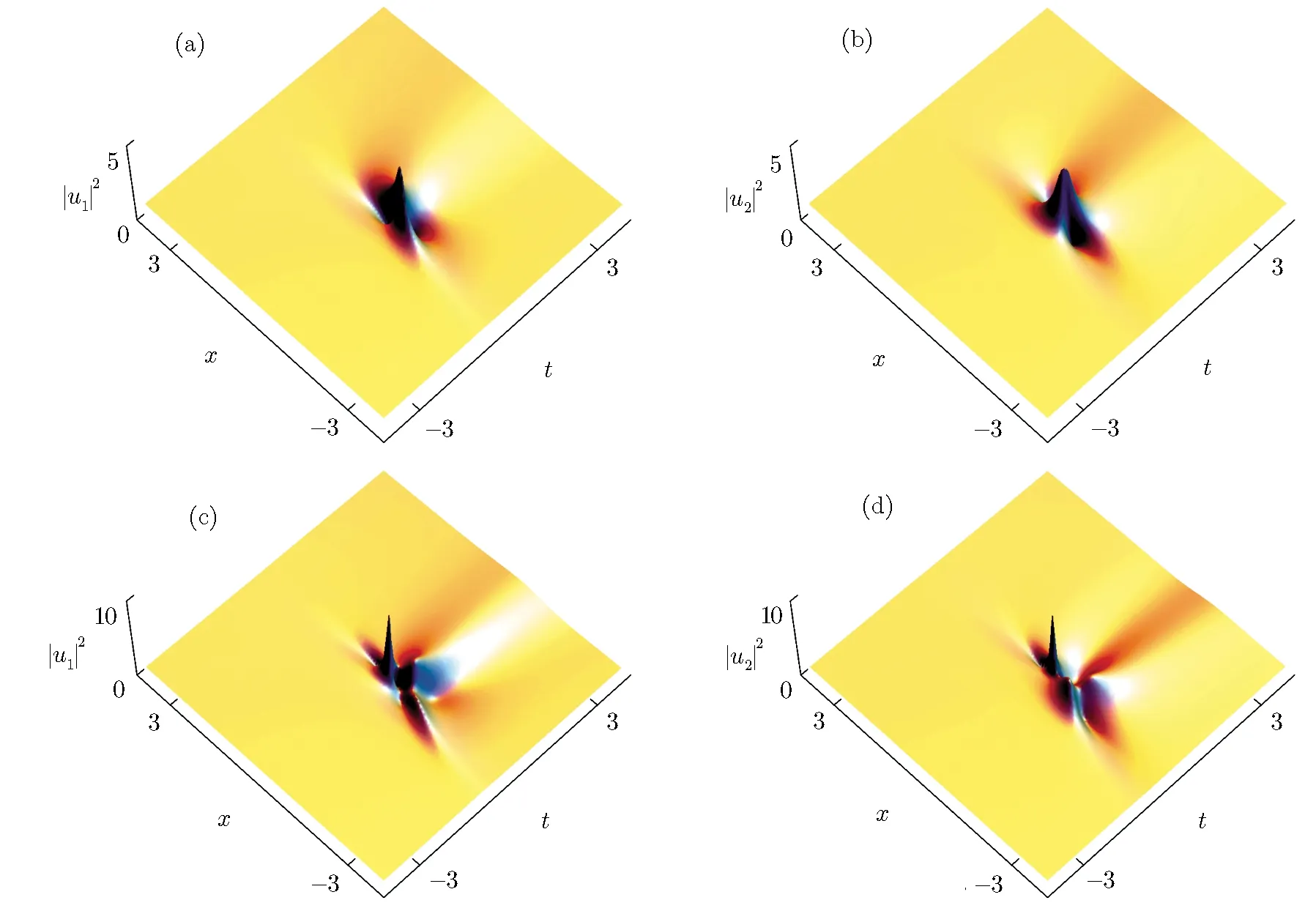
Fig.4 (a),(b)Type-I rogue wave via Solutions(5)with k=l=2,ρ0=m=1,p=0.01,d2=0.5,y=0,β(t)= β1e−β0t,W(t)=er0t/2,γ(t)= γ0/2,β0=0.9,β1=0.5,γ0=0.15;(c),(d)Type-II rogue wave via Solutions(5)with the same parameters as those in Figs.3(a)and 3(b).

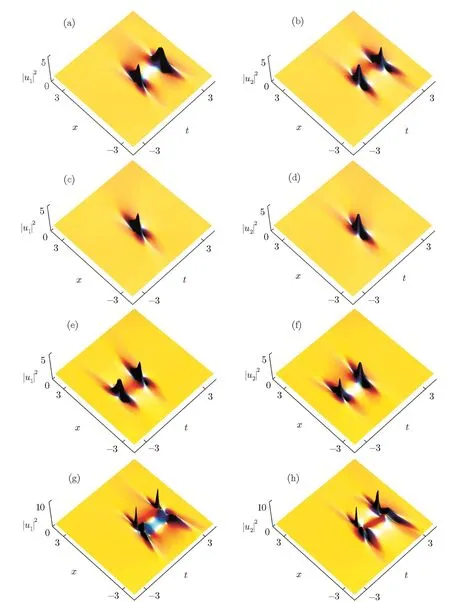
Fig.5 (a),(b)Composite type-I rogue wave via Solutions(5)with k=l=2,ρ0=m=1,p=0.01,d2=0.5,y=0,β(t)= β1− β0t,W(t)=er0t/2,γ(t)= γ0/2,β0=0.7,β1=0.7,γ0=0.15;(c),(d)The same as those in Figs.5(a)and 5(b)except that β0=0.2;(e),(f)The same as those in Figs.5(a),5(b)except that β0= −0.7;(g),(h)Composite type-II rogue wave via Solutions(6)with the same parameters as those in Figs.5(a)and 5(b).

In this section,based on Solutions(5)and(6),we will investigate the effects of the diffraction parameter β(t)on the evolution properties of the rogue waves through choosing several types of function β(t),which is similar to the analysis in Ref.[24].The different expressions of β(t)coefficient of the graded-index waveguide can generate certain structures related to the pulse,e.g.,the exponentially growing periodic function is related the exponentially growing periodic diffraction parameter of the graded-index waveguide,the exponential function corresponds to the exponentially distributed diffraction parameter of the graded-index waveguide,the linear function corresponds to the linear diffraction parameter of the graded-index waveguide,and the quadratic function is related to the quadratic diffraction parameter of the gradedindex waveguide.γ(t)represents the amplification or absorption coefficient:γ(t)>0 denotes the amplification of a pulse,while γ(t)<0 represents the absorption of a pulse.Since x and y have the same influence on Solutions(5)and(6),evolution properties of the Type-I and Type-II rogue waves on the y-t plane are the same as those on the x-t plane,as shown in Figs.1 and 2.Therefore,we only discuss the evolution properties of the rogue waves on the x-t plane.

3.1 Case I

We employ an exponentially-growing-periodic diffraction parameter β(t)= β0eγ0tcos(σt)and a gain parameter γ(t)= γ0/2,with σ being related to the variation period of β(t),and β0, γ0denoting the real constants.[22,31]When σ = γ0=0,Figs.1 and 2 present the type-I and type-II rogue waves,respectively.As shown in Figs.3(a)and 3(b),when σ and γ0are two nonzero constants,displayed on the x-t plane is the periodic type-I rogue wave,whose width increases along the propagation direction t.Occurrence of the periodic rogue wave is due to the presence of a cosine function in β(t).In Figs.3(c)and 3(d),when σ =2.5 and γ0=0.15,periodic type-II rogue wave is similar to the bound state of two solitons.Similarly,width of the type-II rogue wave along the x direction increases.The above results indicate that the width of a rogue wave along the x direction can be enhanced in the optical waveguide with exponentially growing periodic β(t).

3.2 Case II

In Case I,we discuss the propagation of the type-I and type-II rogue waves with β(t)as the exponentially growing periodic diffraction parameter.In this case,we only consider an exponentially diffraction parameter,i.e.,β(t)= β1e−β0t.Figures 4(a)and 4(b)exhibit the type-I rogue wave with a hump along the t direction.For the same β(t),we can observe the type-II rogue wave with a hump along the t direction in Figs.4(c)and 4(d).Compared with Figs.1(a)and 1(b),width of the type-I rogue wave along the t direction enlarges in Figs.4(a)and 4(b).Compared with Figs.2(a)and 2(b),width of the type-II rogue wave along the t direction also enlarges in Figs.4(c)and 4(d).

3.3 Case III

In this case,we will discuss the properties of the rogue waves for System(1)with β(t)= β1− β0t,[32−33]where β1and β0are two constants.When β0=0.7,we get the composite rogue wave consisting of the two separate type-I rogue waves along the direction of t≥0,as shown in Figs.5(a)and 5(b).When β0is equal to 0.2,two type-I rogue waves merge together around t=0 in Figs.5(c)and 5(d).When β0= −0.7,we can see that the type-I rogue wave splits into two rogue waves along the direction of t≤0 and the positions are different from those in Figs.5(a)and 5(b),as shown in Figs.5(e)and 5(f).The same as those in Figs.5(a)and 5(b),Figs.5(g)and 5(h)present the composite rogue wave consisting of the two separate type-II rogue waves.When we decrease the value of β0,type-II rogue wave has the similar behaviors of the type-I rogue wave.

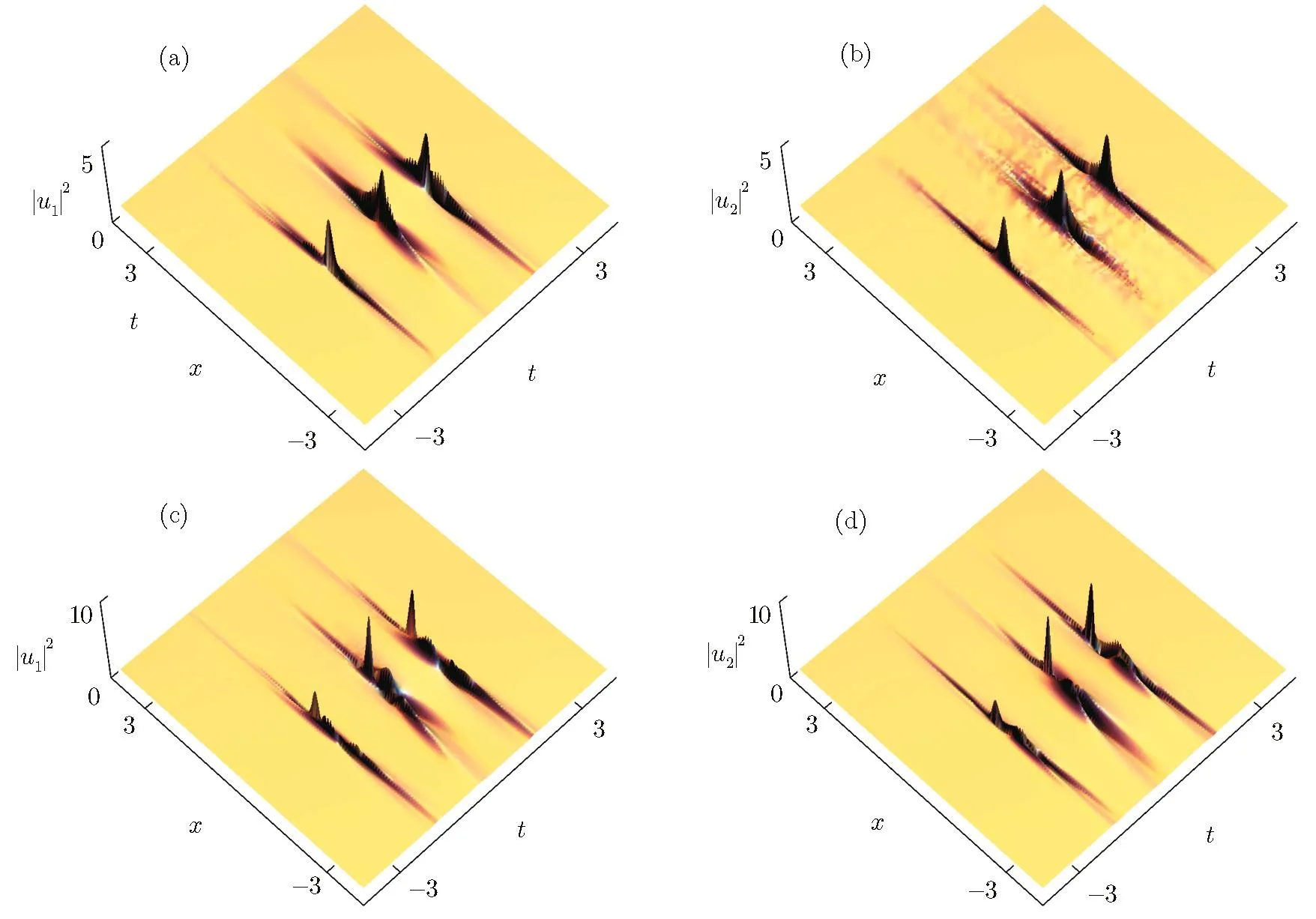
Fig.6 (a),(b)Composite type-I rogue wave via Solutions(5)with k=l=2,ρ0=m=1,p=0.01,d2=0.5,y=0,β(t)= β1− β0t− β2t2,W(t)=er0t/2,γ(t)= γ0/2,β0=0.7,β1=2,β2=2.5,γ0=0.15;(c),(d)Composite type-II rogue wave via Solutions(6)with the same parameters as those in Figs.6(a)and 6(b).

3.4 Case IV

Finally,we take β(t)= β1− β0t− β2t2/2,where β1,β0,and β2are the real constants.[22,34]Figures 6(a)and 6(b)display the type-I composite rogue wave consisting of three separate type-I rogue waves.Composite type-II rogue wave with the three separate type-II rogue waves can be observed in Figs.6(c)and 6(d).

4 Conclusions

In this paper,we have studied a(2+1)-dimensional coupled nonlinear Schrödinger system with variable coefficients,i.e.,System(1),which describes the propagation of an optical beam inside the two-dimensional graded-index waveguide amplifier with the polarization effects.According to Similarity transformation(2),we have derived the type-I and type-II rogue-wave solutions for System(1),i.e.,solutions(5)and(6).We have graphically presented two types of the rouge waves and discussed the influence of the diffraction parameter β(t)on the rogue waves.When the diffraction parameter is exponentially-growing periodic,i.e.,β(t)= β0eγ0tcos(σt),Figs.1 and 2 have displayed type-I and type-II rogue waves:When γ0= σ =0,type-I rogue wave with one largest crest and two valleys has been exhibited in Figs.1(a)and 1(b),type-II rogue wave with one largest crest,two subcrests and two valleys has been presented in Figs.2(a)and 2(b);When γ0and σ are taken as the nonzero constants,periodic type-I and type-II rogue waves have been displayed in Figs.3,respectively.When the diffraction parameter is exponential,i.e.,β(t)= β1e−β0t,Figs.4(a)and 4(b)have exhibited the type-I rogue wave with a hump along the t direction;Similarly,type-II rogue wave with a hump along the t direction has been displayed in Figs.4(c)and 4(d).When the diffraction parameter is linear or quadratic,i.e.,β(t)is β1− β0t or β1− β0t− β2t2/2,we have obtained the composite type-I and type-II rogue waves in Figs.5 and 6.

[1]A.R.Osborne,Nonlinear Ocean Waves,Acad.,New York(2009).

[2]A.R.Osborne,M.Onorato,and M.Serio,Phys.Lett.A 275(2000)386.

[3]M.S.Longuet-Higgins,J.Marine Res.11(1952)1245.

[4]C.Kharif,E.Pelinovsky,and A.Slunyaev,Rogue Waves in the Ocean,Springer,New York(2009).

[5]A.Chabchoub,N.Ho ff mann,M.Onorato,and N.Akhmediev,Phys.Rev.X 2(2012)011015.

[6]A.Chabchoub and N.Akhmediev,Phys.Lett.A 377(2013)2590.

[7]W.J.Liu,Y.J.Zhang,L.H.Pang,et al.,Nonlinear Dyn.86(2016)1069;G.F.Deng and Y.T.Gao,Eur.Phys.J.Plus 132(2017)255;X.Y.Gao,Ocan Engineering 96(2015)245.

[8]T.Xu,C.J.Liu,F.H.Qi,et al.,J.Nonl.Math.Phys.24(2017)116;T.Xu,M.Li,Y.H.Huang,et al.,Mod.Phys.Lett.B 31(2017)1750338;Q.M.Huang and Y.T.Gao,Nonlinear Dyn.89(2017)2855;Q.M.Huang,Y.T.Gao,and L.Hu,Appl.Math.Lett.75(2018)135.

[9]P.Jin,C.A.Bouman,and K.D.Sauer,IEEE Trans.comput.Imaging 1(2015)200.

[10]W.R.Sun,D.Y.Liu,and X.Y.Xie,Chaos 27(2017)043114.

[11]R.Guo,H.H.Zhao,and Y.Wang,Nonlinear Dyn.83(2015)2475.

[12]D.R.Solli,C.Ropers,P.Koonath,and B.Jalali,Nature(London)450(2007)1054.

[13]M.Li,T.Xu,and D.X.Meng,J.Phys.Soc.Jpn.85(2016)124001.

[14]M.Li,H.Liang,T.Xu,and C.J.Liu,Eur.Phys.J.Plus 131(2016)100.

[15]W.M.Moslem,Phys.Plasmas 18(2011)032301.

[16]G.P.Veldas,J.Borhanian,M.Mckerr,et al.,J.Opt.15(2013)064003.

[17]Y.V.Bludov,V.V.Konotop,and N.Akhmediev,Phys.Rev.A 80(2010)033610.

[18]C.Q.Dai and J.F.Zhang,Opt.Lett.35(2010)2651;Y.Y.Wang,C.Q.Dai,G.Q.Zhou,et al.,Nonlinear Dyn.87(2017)67;C.Q.Dai,J.Liu,Y.Fan,and D.G.Yu,Nonlinear Dyn.88(2017)1373.

[19]A.Zaviyalov,O.Egorov,R.Iliew,and F.Lederer,Phys.Rev.A 85(2012)013828.

[20]A.Coillet,J.Dudley,G.Genty,et al.,Phys.Rev.A 89(2014)013835.

[21]K.Hammani,C.Finot,J.M.Dudley,and G.Millot,Opt.Exp.16(2008)16467.

[22]K.Manikandan,M.Senthilvelan,and R.A.Kraenkel,Eur.Phys.J.B 89(2016)218.

[23]G.P.Agrawal,Nonlinear Fiber Optics,Acad.,San Diego(2007).

[24]M.Li,T.Xu,L.Wang,and F.H.Qi,Appl.Math.Lett.60(2016)8;X.Y.Gao,Appl.Math.Lett.73(2017)143;Z.Z.Lan and B.Gao,Appl.Math.Lett.79(2018)6;T.T.Jia,Y.Z.Chai,and H.Q.Hao,Superlattices Microstruct.105(2017)172;X.Y.Xie and Z.H.Yan,Appl.Math.Lett.80(2018)48;J.J.Su and Y.T.Gao,Eur.Phys.J.Plus 132(2017)53;G.F.Deng and Y.T.Gao,Superlattices Microstruct.109(2017)345.

[25]H.P.Zhu and Z.H.Pan,Laser Phys.24(2014)045406.

[26]H.Y.Wu and H.J.Jiang,Nonlinear Dyn.83(2016)713.

[27]D.K.Kumar,T.S.Raju,C.N.Kumar,and P.K.Panigrahi,J.Mod.Opt.63(2105)1196.

[28]X.Y.Xie,B.Tian,W.R.Sun,and Y.Sun,Commun.Nonlin.Sci.Numer.Simul.29(2015)300.

[29]C.Q.Dai,D.S.Wang,L.L.Wang,et al.,Ann.Phys.326(2011)2356;Y.Y.Wang,L.Chen,C.Q.Dai,et al.,Nonlinear Dyn.90(2017)1269.

[30]B.L.Guo and L.M.Ling,Chin.Phys.Lett.28(2011)110202.

[31]C.Q.Dai,S.Q.Zhu,L.L.Wang,and J.F.Zhang,Europhys.Lett.92(2010)24005.

[32]L.Wang,M.Li,and F.H.Qi,Z.Naturforsch.A 70(2015)251.

[33]L.Wang,M.Li,F.H.Qi,and C.Geng,Eur.Phys.J.D 69(2015)108.