Viscosity Effects on Anisotropic Universe in Curvature-Matter Coupling Gravity

M.Sharif and Aisha Siddiqa

Department of Mathematics,University of the Punjab,Quaid-e-Azam Campus,Lahore-54590,Pakistan

1 Introduction

The accelerating expansion of the universe is a revolutionary discovery which provides a milestone in cosmology.The reason behind this expansion is assumed to be a hypothetical form of negative pressure named as dark energy.This is the most dominated factor in the energy budget of the universe.There have been many proposals to resolve the puzzling nature of dark energy.One of these proposals is to modify geometric part of the Einstein-Hilbert action leading to modified theories of gravity.

A simple generalization of general relativity is obtained by replacing the Ricci scalar R by f(R)in the Einstein-Hilbert action.Harko et al.[1]proposed f(R,T)gravity as a generalized modified theory,where T denotes trace of the energy-momentum tensor.The dependence on T is included due to the considerations of exotic fluids or quantum effects.The coupling of curvature and matter leads to a source term which is expected to yield interesting results.It can produce a matter-dependent deviation from geodesic motion and also worthwhile to discuss dark energy,dark matter interactions as well as late time acceleration.[2]

Jamil et al.[3]introduced some cosmic models in this gravity and found that ΛCDM model is reproduced by dust fluid.Houndjo[4]discussed matter dominated and accelerated phases of the universe for the models linear in T while the power of R depends on input parameters.Sharif and Zubair[5]explored thermodynamics of this gravity and concluded that the second law of thermodynamics is valid for phantom as well as non-phantom phases.In Refs.[6]–[8],the higher dimensions are also explored in the framework of f(R,T)gravity.Moraes et al.[9]studied hydrostatic equilibrium condition for neutron stars with a specific form of equation of state(EoS)and found that the extreme mass can cross observational limits.Sharif and Nawazish[10]worked on the existence of Noether symmetries interacting with generalized scalar field model in f(R,T)gravity.They found that dust fluid leads to decelerated expansion while perfect fl uid yields current cosmic expansion for quintessence model.

Recent experimental data supports anisotropic nature of the universe which tends towards isotropic with the passage of time.[11−13]To study the anisotropic background of cosmos,Bianchi type models have frequently been considered in Refs.[14]–[17].Bianchi type-I model is the simplest generalization of FRW spacetime.Sharif and Waheed[18]investigated this model in Brans-Dicke theory and concluded that anisotropic fl uid tends to become isotropic at later times.Reddy and Kumar[19]examined Bianchi type-III model in f(R,T)theory and observed no initial singularity as well as late time cosmic expansion.Sharif and Saleem[20]studied warm in fl ation for LRS Bianchi type-I model and showed that this model is consistent with observational data.

Bulk viscosity plays a significant role in cosmology as dissipative processes are thought to be present in any viable theory of cosmic evolution,which may lead to interesting conclusions.Johri and Sudharsan[21]investigated the effects of bulk viscosity on the evolution of FRW universe and found that time independent bulk viscosity can drive a steady state universe.Ren and Meng[22]presented a study on scalar field with bulk viscosity and proposed a model for which ΛCDM is a special case.They concluded that bulk viscosity enhances expansion of the universe.Gagnon and Lesgourgues[23]discussed a bulk viscous model as an alternative to dark energy.Singh and Kumar[24]explored the role of bulk viscosity in f(R,T)gravity for FRW model with perfect fluid and found that bulk viscosity provides a supplement for expansion.

This paper deals with the evolution of viscous fluid in f(R,T)gravity with LRS Bianchi type-I model.The plan of paper is as follows.In the next section,we formulate the field equations and an evolution equation for H.We discuss the scale factors as well as deceleration parameter and conditions for the occurrence of big-rip singularity for different viscosity models.The last section summarizes the obtained results.

2 Anisotropic Universe with Viscous Fluid

The action for f(R,T)gravity is defined as

Variation of the above action with respect to gαβgives the field equations

where f=f(R,T),fR= ∂f/∂R,fT= ∂f/∂T,and Θαβis evaluated by

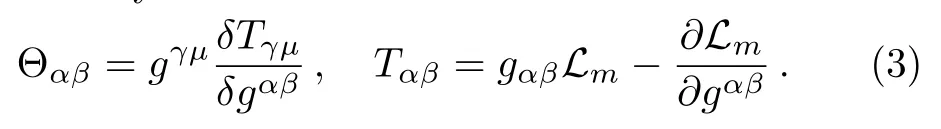
Harko et al.[1]introduced the model f(R,T)=R+2f(T)while f(T)= χ(T)nis taken in Ref.[25],where χ and n are real constants. Thus we can write f(R,T)=R+2χT,[24]which simplifies the field equations as

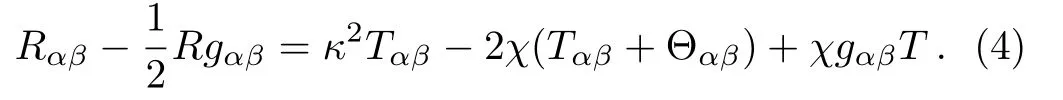
The LRS Bianchi type-I universe model is taken as

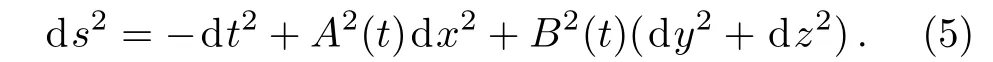
We assume that shear and expansion scalars are proportional to each other(σ ∝ Θ),which gives A=Bm(where m0 is a constant).[26]The mean Hubble parameter then becomes

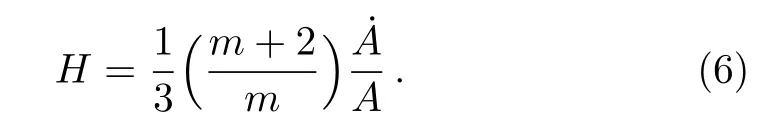
The field equations for this metric are

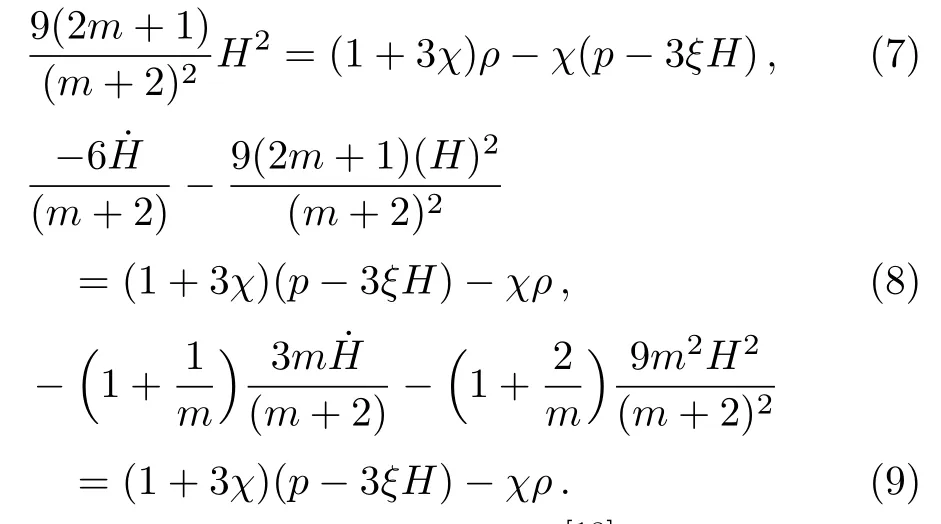
The anisotropy parameter is given by[18]

where Hirepresent directional Hubble parameters.We evaluate Apas

The relation between m and Apis given in Table 1.

Table 1 Relation of m and Ap.

The energy-momentum tensor of viscous fluid is considered as[24]

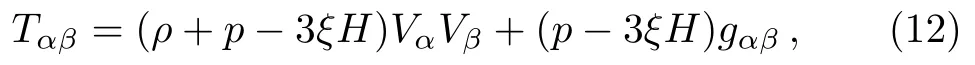
where ρ denotes matter density,p represents pressure,Vαis four velocity and ξ denotes bulk viscosity.The trace of energy-momentum tensor is

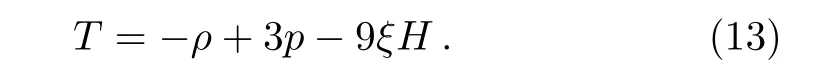
The first two field equations produce the differential equation in H

To solve this equation for H,we consider the following EoS

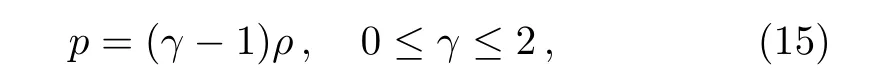
and an expression for bulk viscosity of the form[24]

where ξ0and ξ1are constants.The matter density is evaluated using Eqs.(15)and(16)in Eq.(7)as

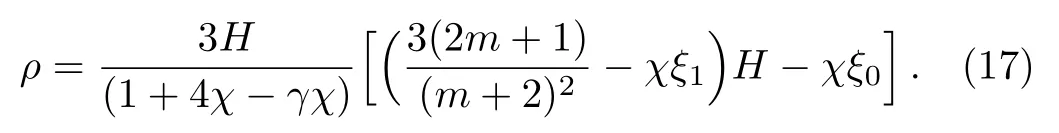
In the following,we consider four different viscosity models and evaluate the expressions for H,A,B,ρ,and q.

2.1 Fluid with Zero Viscosity(ξ=0)

For a non-viscous fluid,Eq.(14)becomes

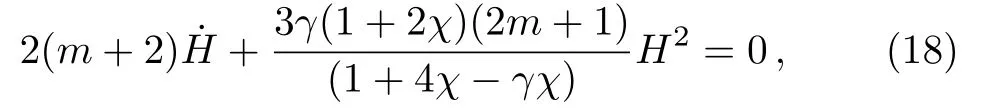
where we have used Eqs.(16)and(17).The solution of this equation for γ0 is given by

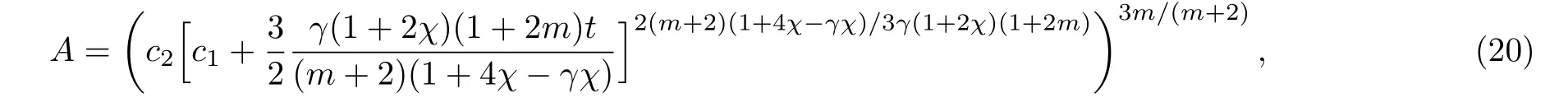
where c1is a constant of integration.The Hubble parameter yields here c2>0 is another integration constant.This represents a power-law type solution of the scale factor.The scale factor B can be found using A=Bm⇒B=A1/m.The deceleration parameter is obtained as

which is time independent and its value varies with γ, χ and m.

For different values of γ,we have different evolutionary eras.Here,we present a discussion for the dark energy dominated era corresponding to γ=0.Solving Eq.(18)for γ=0,we have

>0 and>0 are constants of integration.The scale factors are of exponential form.For m=1,the above values correspond to de Sitter universe.The plots for A and B in Eq.(23)are given in Fig.1.The behavior of both graphs is increasing with time while anisotropy has opposite effects(it increases A and decreases B).Equation(17)yields the expression for density as

There is a big-rip singularity when ρ → ∞,i.e.,for a non-viscous fluid,big-rip is expected only if m=−2 or χ=−1/4.For m=−2,the anisotropy parameter Ap(11)also approaches to infinity.

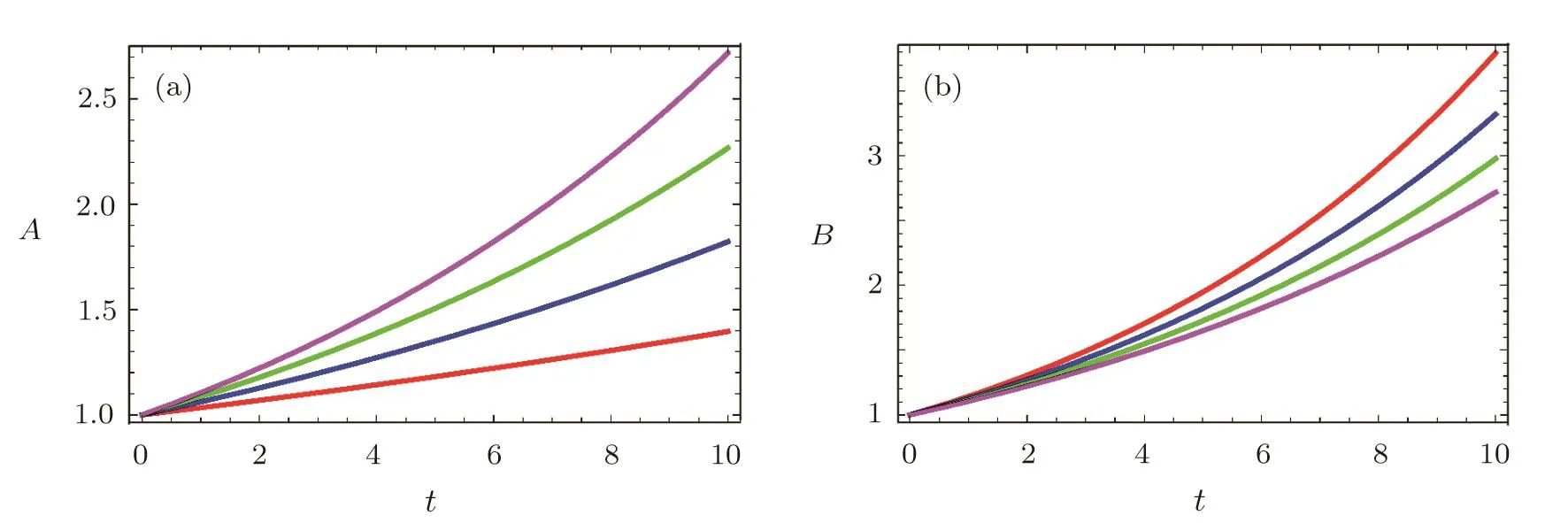
Fig.1 (Color online)Plots of A and B versus t for ξ=0 and fixing c′1=0.1,c′2=1,m=0.25(red),0.5(blue),0.75(green)and 1(purple).

2.2 Fluid with Constant Viscosity(ξ = ξ0)

In this case,for γ0 Eq.(14)yields the solution

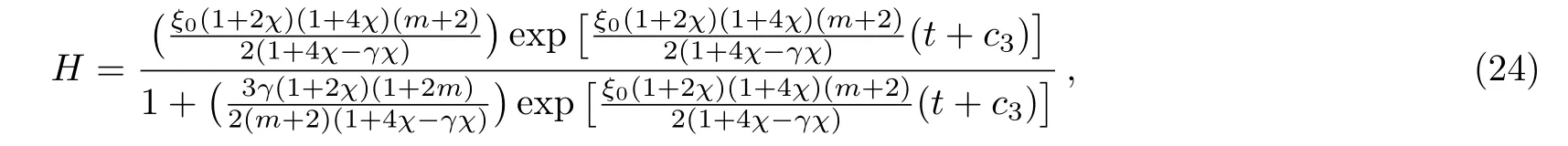
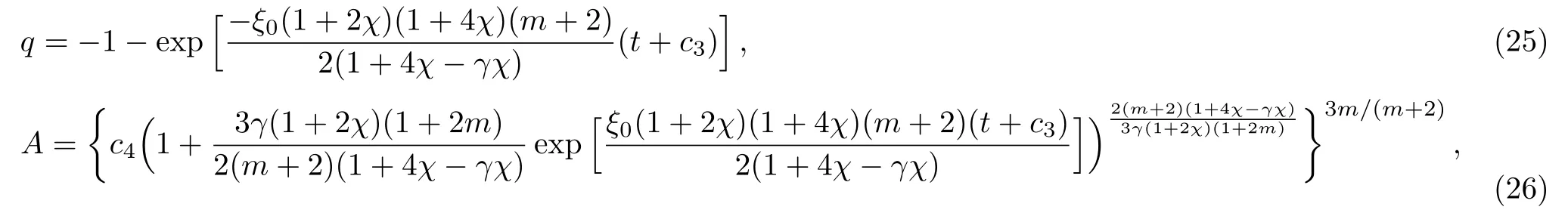
where c3is an integration constant.Using the above equation,q and A are evaluated as c4>0 is another integration constant.The scale factors become exponential type.For γ=0,we have

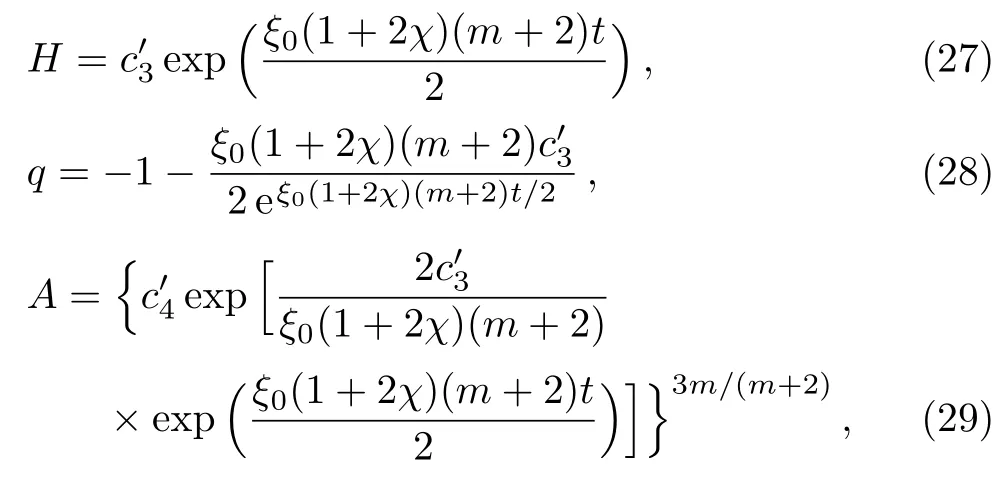
hereand>0 are constants of integration.The graphical behavior of q,A and B are shown in Fig.2.The decrease in anisotropy has the same effects as for zero viscosity fluid while increase in bulk viscosity shows decrease in both A and B.The deceleration parameter is negative and does not cross the line q=−1.The decrease in m as well as increase in ξ0decreases the value of q.For a constant viscous fluid,the matter density in dark energy dominated era is obtained as

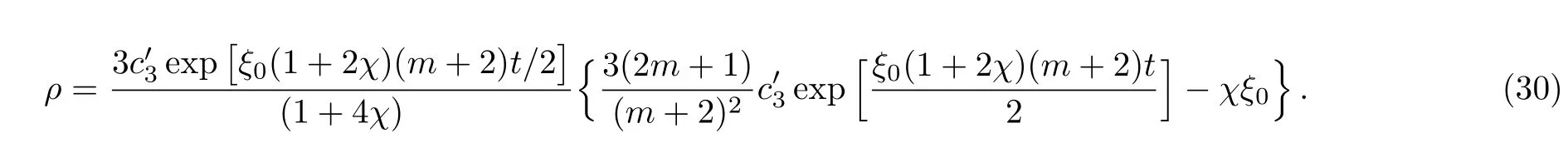
Again ρ → ∞ or big-rip occurs when m= −2 or χ = −1/4.This also holds for the next two cases and we can obtain an expression of time for the big-rip occurrence there.

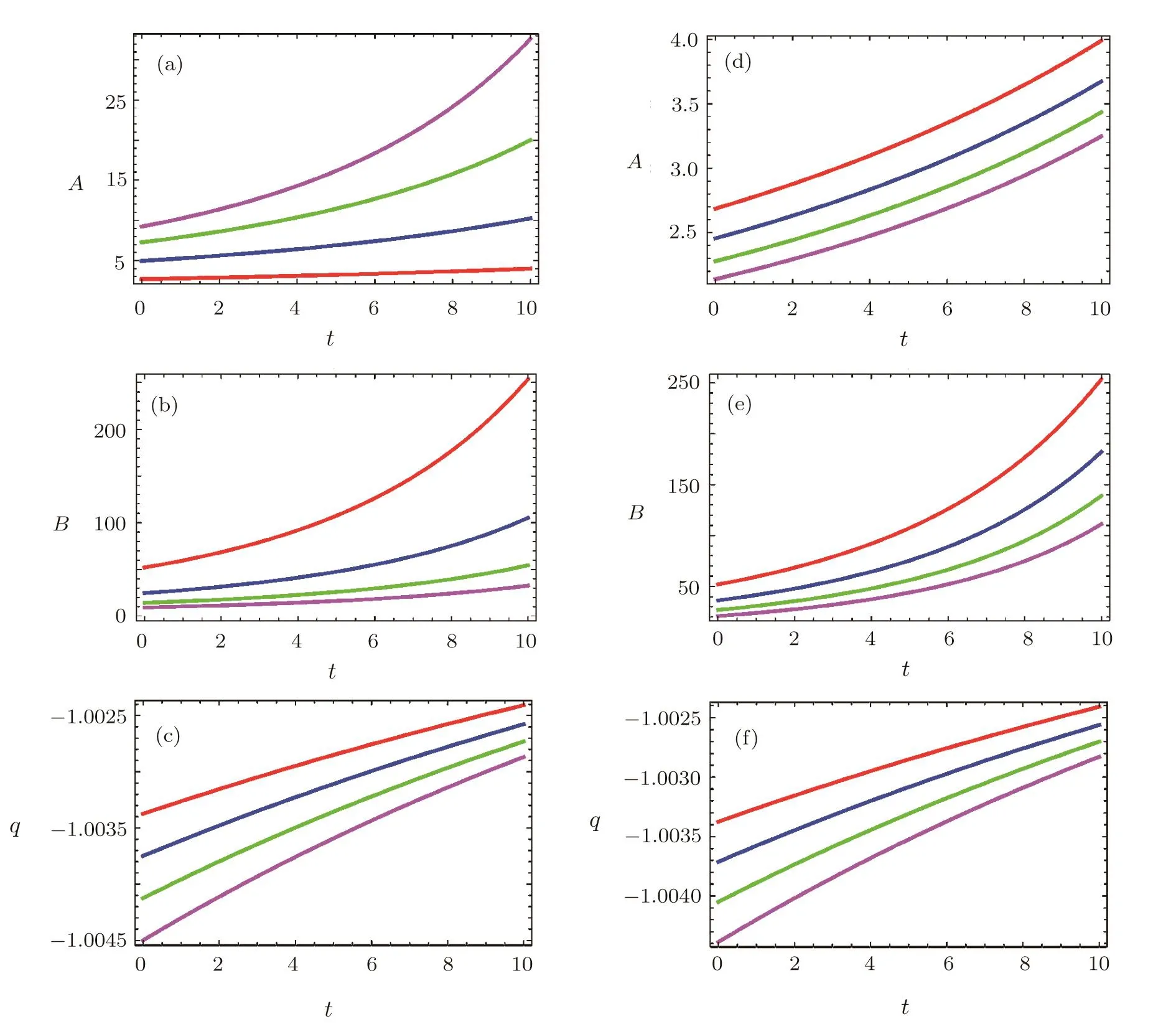
Fig.2 (Color online)Plots of A,B and q versus t for ξ= ξ0and fixing χ =1,c′3=0.1,c′4=1, ξ0=0.01,m=0.25(red),0.5(blue),0.75(green)and 1(purple)in(a),(b),(c)and fixing m=0.25,ξ0=0.01(red),0.011(blue),0.012(green)and 0.013(purple)in(d)(e)(f).

2.3 Fluid with Viscosity Proportional to H(ξ = ξ1H)

In this case,the solution of Eq.(14)for 0≤γ≤2 is

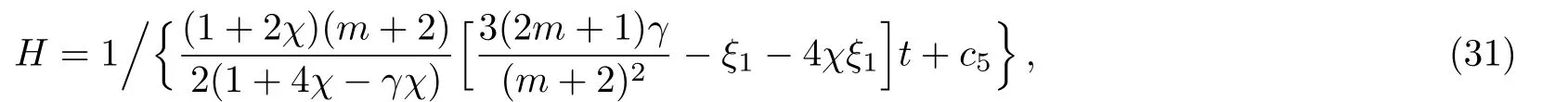
c5represents constant of integration.Similarly,q and A can be obtained as

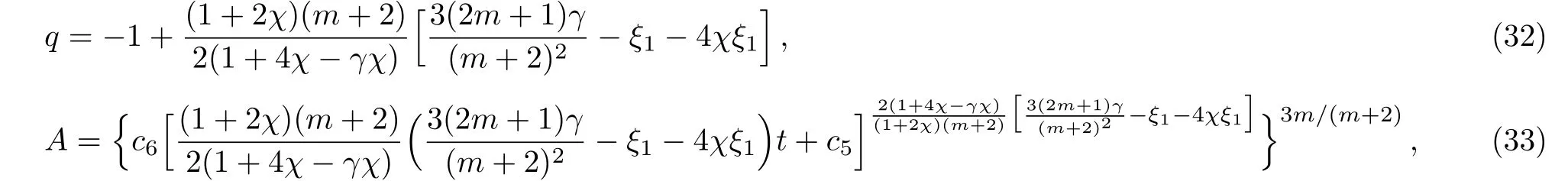
c6>0 denotes another integration constant.We see that q has a time independent expression as in the first case and A is of power-law type.The scale factor B is obtained in a similar manner.For γ=0,the above expressions reduce to

The value of q depends on χ,m as well as ξ1and remains less than −1 for positive values of all these constants.The plots of A are shown in Fig.3.Here the decrease in m and increase in ξ1yield an increase in A.We see that the effects of viscosity are same on both A and B while anisotropy has opposite effects on both.So,we only show the graphs of A in this case as well as in next one.For this viscosity model and γ =0,ρ becomes

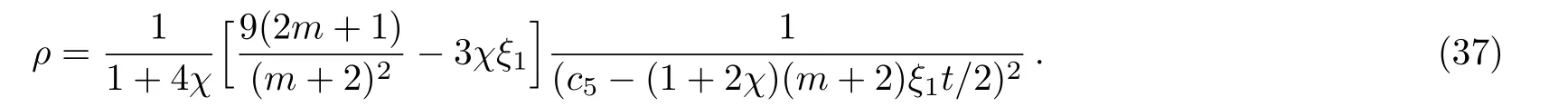
In this case,there is an additional term as compared to the previous cases whose zero value makes density infinite i.e.,

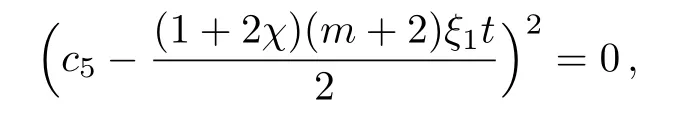
giving the time of big-rip occurrence

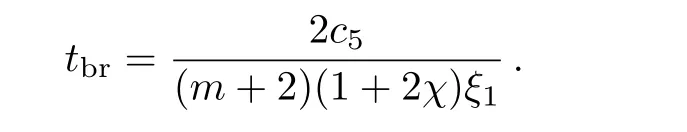
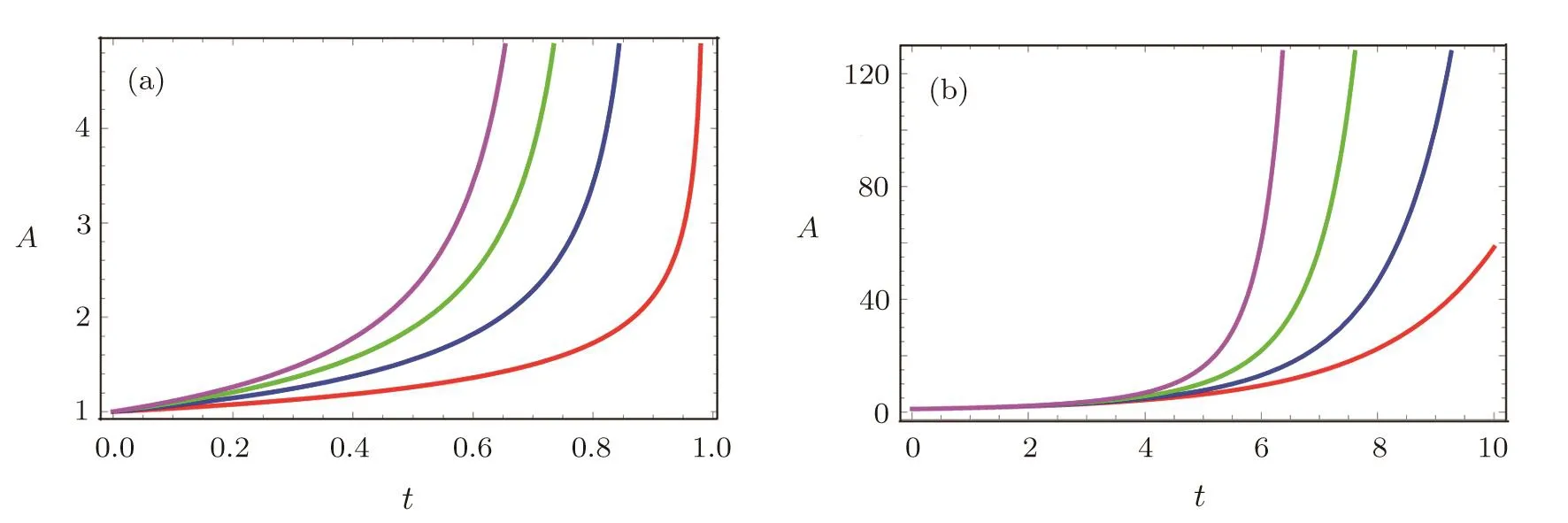
Fig.3 (Color online)Plots of A versus t for ξ= ξ1H and fixing χ =1,c5=1,c6=1, ξ1=0.01,m=0.25(red),0.5(blue),0.75(green)and 1(purple)in(a)and fixing m=0.25,ξ1=0.01(red),0.012(blue),0.014(green)and 0.016(purple)in(b).

2.4 Fluid with Viscosity of the Form ξ = ξ0+ ξ1H

For this viscosity model and 0≤γ≤2,Eq.(14)has the following solution

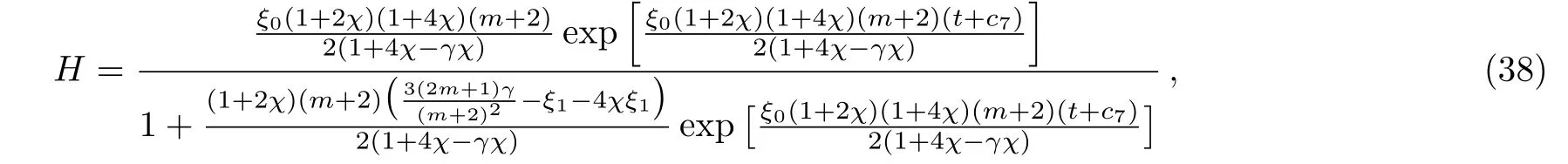
leading the expressions of q and A to

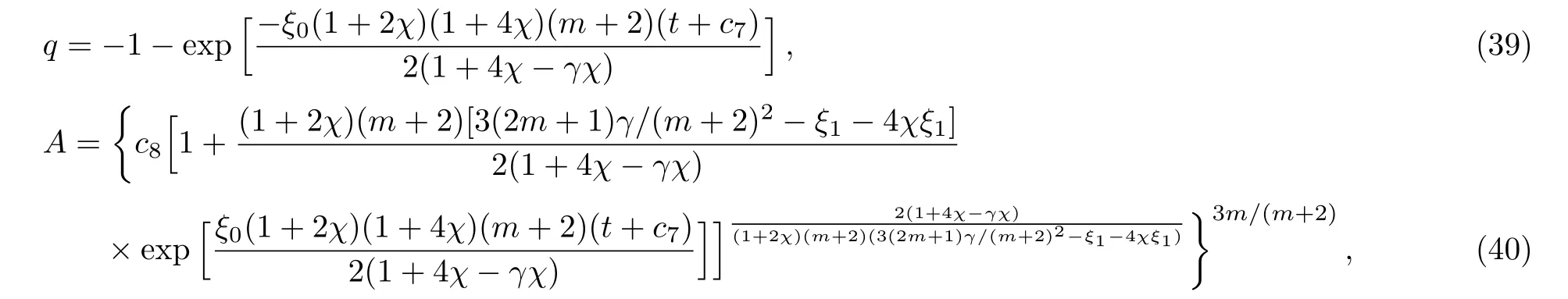
where c7and c8are integration constants with c8>0.Here A has an exponential form and for γ=0,we obtain

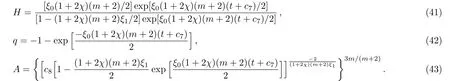
The behavior of scale factor A is shown in Figs.4 and 5.The effects of anisotropy and viscosity on scale factors are the same as in the previous case.The plots of deceleration parameter in Fig.6 indicate that it increases with decrease in anisotropy and increase in viscosity.Also,its value does not cross the line q= −1.Similarly,ρ is obtained as

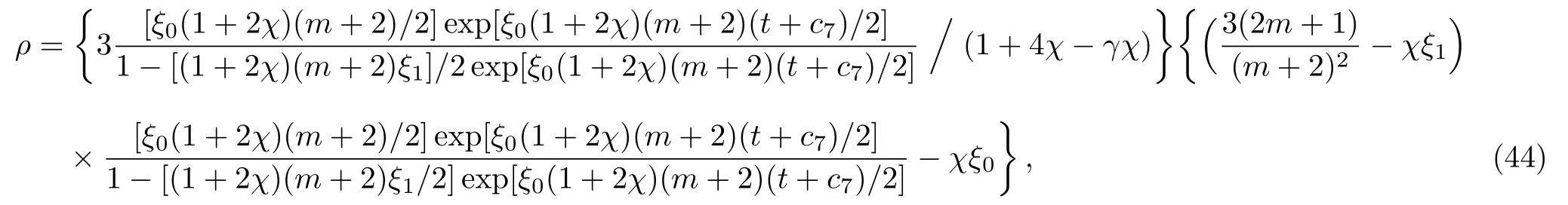
and the time of big-rip is given by

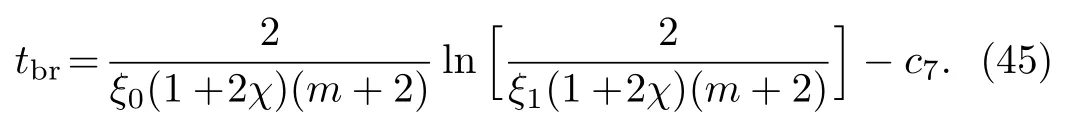
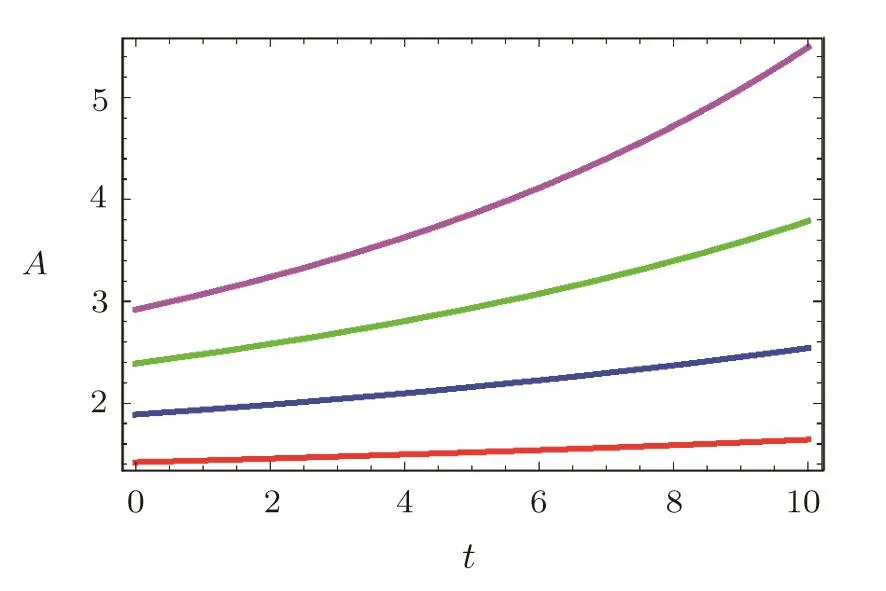
Fig.4 (Color online)Plot of A versus t for ξ= ξ0+ξ1H and fixing χ =1,c7=1,c8=1, ξ0=0.01, ξ1=0.01,m=0.25(red),0.5(blue),0.75(green)and 1(purple).

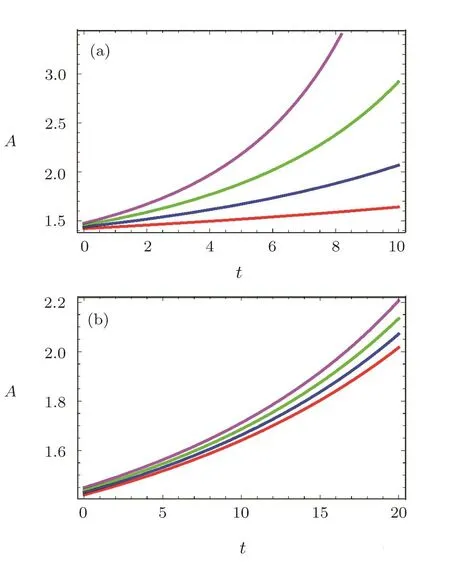
Fig.5 (Color online)Plots of A versus t for ξ= ξ0+ξ1H and fixing χ =1,c7=1,c8=1, ξ1=0.01,m=0.25,ξ0=0.01(red),0.02(blue),0.03(green)and 0.04(purple)in(a)and fixing m=0.25, ξ0=0.01, ξ1=0.01(red),0.02(blue),0.03(green)and 0.04(purple)in(b).

Fig.6 (Color online)Plots of q versus t for ξ= ξ0+ξ1H and fixing χ =1,c7=1,c8=1, ξ0=0.01,m=0.25(red),0.5(blue),0.75(green)and 1(purple)in(a)and fixing m=0.25,ξ0=0.01(red),0.02(blue),0.03(green)and 0.04(purple)in(b).

3 Concluding Remarks

Our universe is homogeneous and isotropic on large scale but there are anisotropies present on small scales.Also,the bulk viscosity is an important candidate in describing early and late time expansion.Thus it would be worthwhile to explore a deviation from isotropy as well as the effects of bulk viscosity on the evolution of cosmos.In this paper,the evolution of scale factors and deceleration parameter in dark energy dominated era with different forms of viscosity is discussed.The graphical analysis is summarized in Tables 2 and 3.The evolution of scale factors with the decrease in anisotropy remain the same in all cases as shown in Table 2.On the other hand,the increase in viscosity has different effects on scale factors.It produces a decrease in scale factors for ξ= ξ0while an increase for ξ= ξ1H as well as ξ= ξ0+ ξ1H.The increase in scale factors with time supports accelerated expansion while an increase in their value with decrease in anisotropy or increase in viscosity show an enhancement in expansion.

It is observed from Table 3 that decrease in anisotropy as well as increase in viscosity decreases q for second and third bulk viscosity models while increases for the last model.The negative value of q indicates an accelerated expansion of the universe and we have q≤ −1 for all cases.Hence,the expansion is enhanced due to bulk viscosity for ξ0and ξ= ξ1H.For each case,m= −2 and χ=−1/4 are the common conditions for the occurrence of big-rip.For the last two viscosity models,we have also an expression of time at which big-rip could occur.We would like to mention here that for m=1,our results reduce to that of isotropic case.[24]It is concluded that the accelerated expansion is faster for ξ= ξ1H as compared to other models.

Table 2 Evolution of scale factors.

Table 3 Evolution of deceleration parameter.

Acknowledgments

We would like to thank the Higher Education Commission,Islamabad,Pakistan for its financial support through the Indigenous Ph.D.5000 Fellowship Program Phase-II,Batch-III.

[1]T.Harko,F.S.N.Lobo,S.Nojiri,and S.D.Odintsov,Phys.Rev.D 84(2011)024020.

[2]T.Harko and F.S.N.Lobo,Galaxies 2(2014)410.

[3]M.Jamil,D.Momeni,M.Raza,and R.Myrzakulov,Eur.Phys.J.C 72(2012)1999.

[4]M.J.S.Houndjo,Int.J.Mod.Phys.D 21(2012)1250003.

[5]M.Sharif and M.Zubair,J.Cosmol.Astropart.Phys.03(2012)28.

[6]P.H.R.S.Moraes,Eur.Phys.J.C 75(2015)168.

[7]P.H.R.S.Moraes and R.A.C.Correa,Astrophys.Space Sci.361(2016)91.

[8]R.A.C.Correa and P.H.R.S.Moraes,Eur.Phys.J.C 76(2016)100.

[9]P.H.R.S.Moraes,D.V.A.Jos´e,and M.Malheiro,J.Cosmol.Astropart.Phys.06(2016)005.

[10]M.Sharif and I.Nawazish,Eur.Phys.J.C 77(2017)198.

[11]C.L.Bennett,et al.,Astrophys.J.Suppl.Ser.148(2003)1.

[12]A.de Oliveira-Costa,M.Tegmark,M.Zaldarriaga,and A.Hamilton,Phys.Rev.D 69(2004)063516.

[13]D.J.Schwarz,G.D.Starkman,D.Huterer,and C.J.Copi,Phys.Rev.Lett.93(2004)221301.

[14]C.P.Singh,S.Ram,and M.Zeyauddin,Astrophys.Space Sci.315(2008)181.

[15]M.Sharif and M.F.Shamir,Class.Quantum Grav.26(2009)235020.

[16]E.Wilson-Ewing,Phys.Rev.D 82(2010)043508.

[17]D.R.K.Reddy,R.Santikumar,and R.L.Naidu,Astrophys.Space Sci.342(2012)249.

[18]M.Sharif and S.Waheed,Eur.Phys.J.C 72(2012)1876.

[19]D.R.K.Reddy and R.S.Kumar,Astrophys.Space Sci.344(2013)253.

[20]M.Sharif and R.Saleem,Eur.Phys.J.C 74(2014)2738.

[21]V.B.Johri and R.Sudharsan,Phys.Lett.A 132(1988)316.

[22]J.Ren and X.H.Meng,Phys.Lett.B 636(2006)5.

[23]J.S.Gagnon and J.Lesgourgues,J.Cosmol.Astropart.Phys.09(2011)026.

[24]C.P.Singh and P.Kumar,Eur.Phys.J.C 74(2014)3070.

[25]D.Bazeia,A.S.Lob˜ao,and R.Menezes,Phys.Lett.B 743(2015)98;P.H.R.S.Moraes and J.R.L.Santos,Eur.Phys.J.C 76(2016)60.

[26]M.Sharif and S.Waheed,Phys.Lett.B 726(2013)1.