Sequential Quantum Secret Sharing Using a Single Qudit∗

Chen-Ming Bai(白晨明),Zhi-Hui Li(李志慧),,† and Yong-Ming Li(李永明)

1College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China

2College of Computer Science,Shaanxi Normal University,Xi’an 710119,China

1 Introduction

Secret sharing, firstly introduced by Shamir[1]and Blakley,[2]is a cryptographic primitive which plays a significant role in the various secure multiparty computation tasks and management of keys.Secret sharing has extended to the quantum field.[3−9]Quantum secret sharing(QSS)is also a cryptographic protocol to distribute either a classical secret(string of bits)or a quantum secret(unknown quantum state)to a group of players P such that only authorized subsets of P can collaboratively recover the secret.The security of most classical cryptographic systems is based on the assumptions of computational complexity,which might be broken by the strong power of advanced algorithms,such as Shor algorithm.In addition,another main drawback of classical secret sharing schemes is that they are not perfectly secure from an eavesdropper attack.Compared to the classical one,QSS can enforce the security for cryptographic tasks due to the quantum no-cloning theorem and uncertainty properties of quantum mechanics.[10−11]In 1999,Hillery et al.[3]firstly introduced a protocol of QSS by using GHZ states.At the same year,Karlsson et al.[12]showed how a QSS protocol can be implemented using two-particle quantum entanglement and discussed how to detect eavesdropping or a dishonest participant.In 2004,Xiao et al.[13]generalized the QSS of Hillery et al. into arbitrary multipartite entangled state.From then on,various QSS schemes have been proposed.[14−23]Many scholars gave QSS schemes based on different principles,such as quantum error-correcting code[24]and local distinguishability of quantum states.[25−29]In these works,it has been shown that QSS is not only a mere theoretical concept,but also an experimental possibility.[30]

With the development and application of quantum communication,it is a great idea to design a quantum protocol with a single state.Recently,Tavakoli et al.[31]proposed a model of(n,n)-threshold secret sharing with a single d-level quantum system(for any prime d).This model has huge advantages in scalability and can be realized with state-of-the-art technology.However,in this scheme,there are two deficiencies.Firstly,the successful probability of each round is dependent on d measurement bases,that is,the efficiency is 1/d.With the increase of d,the efficiency of this scheme will be very low.In order to improve this problem,Karimipour et al.[32]proposed a QSS with a random walk in a lattice of states for arbitrary d.With this random walk picture at hand,they can improve their scheme efficiency to reach 1/2.Although the efficiency has been improved,Lin et al.[33]found that their scheme was not secure for one dishonest who can recover the secret without the help of other participants.Secondly,Tavakoli’s scheme is just an(n,n)-threshold and not suitable for a general access structure.For the problem,Lu et al.[34]proposed a(t,n)-threshold QSS scheme based on a single d-level quantum system.In this scheme,they employed the classical Shamir’s(t,n)-threshold secret sharing.However,it cannot be applied to the general access structure.The general access structure of a secret sharing scheme is a family of all authorized sets.In general,access structures are considered to be monotone,i.e.,any superset of an authorized set must be authorized.Because each person has different weight in real life,the ability to recover the secret is different.Therefore,this general access structure is of practical significance and plays a major role in secret sharing schemes.

In this paper,we propose a new QSS scheme,which can solve the above two problems.For the first problem,the distributor Alice in our scheme voluntarily chooses the measurement bases and sends them to all participants through quantum secure direct communication.[35]This operation can not only improve the efficiency of the protocol but also reduce the possibility of information leakage.Through this method,the efficiency of our scheme can reach 1.For the second problem,we treat each authorized set as a small threshold scheme.By cascading method,we apply our scheme to the general access structure,which makes it more practical.In particular,if the access structure contains only one authorized set,our scheme will be the same as Tavakoli’s.Therefore,our scheme is more extensive and meaningful.

The structure of the paper is organized as follows.In Sec.2,we give some preliminaries.In Sec.3,we propose the quantum secret sharing scheme for a general access structure and show an example.Section 4 analyzes the security and compares our scheme with the existing scheme.Finally,the conclusion is given in Sec.5.

2 Preliminaries

In this section we briefly recall some basic concepts such as the access structure and mutually unbiased(orthonormal)bases.

2.1 Access Structure

Let P be a set of players,then the authorized set is a subset of P,which can reconstruct the original secret.The access structure Γ of a secret sharing scheme is a family of all authorized sets.In general,access structures are considered to be monotone increasing,i.e.,any superset of an authorized set must be authorized.For A,A′⊆ P,if A ∈ Γ and A ⊆ A′,then A′∈ Γ.The basis of Γ is the collection of all minimal authorized sets of P.We assume that every participant belongs to at least one minimal authorized set.

2.2 Mutually Unbiased Bases and Unitary Operation

Mutually unbiased bases(MUBs)are the important tool in many quantum information processing.As noted in Refs.[36–37],it is possible to find d+1 MUBs in d-dimensional quantum system only if d is(any power of prime numbers)an odd prime. At first,the computational basis is denoted by{|k⟩|k ∈ D},where D={0,...,d−1}.For consistency,we also restrict d to odd prime number in the whole article.

Besides the computational basis,the explicit forms of the remaining d sets of MUBs are

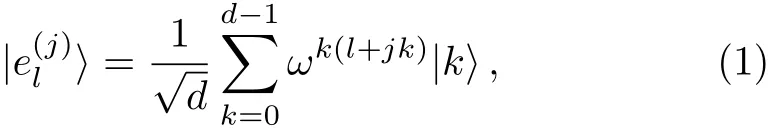
where ω =e2πi/d,j ∈ D labels the basis and l∈ D enumerates the vectors of the given basis.They are mutually unbiased because the overlap is

In Ref.[31],the encoding operation consists of two unitary operators,Xdand Yd,which are depicted as follows:

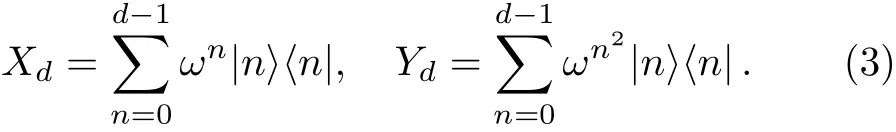
Using Eqs.(1)and(3),we can get

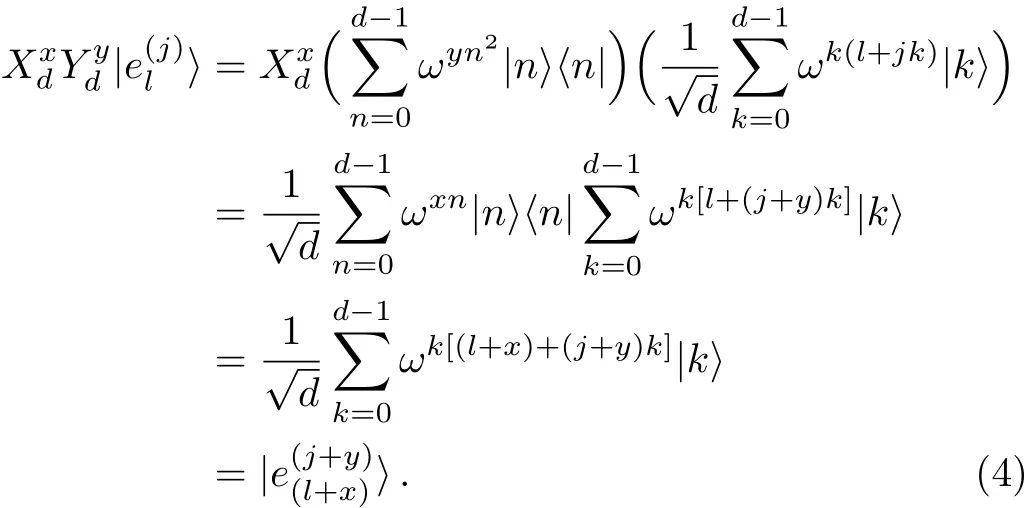
For convenience,the operatoris written as Ux,y,

3 The QSS Scheme on Access Structure

In this section,we propose our scheme using a single qudit to realize a general access struture.Assume that the distributor Alice wants to share secret messages to a group P with n participants,and the general access structure is denoted by

where Ai(i=1,2,...,r)is the minimal authorized set.

By cascading method,we utilize our new scheme to implement the general access structure Γ,which every minimal authorized set Aican be realized by a small threshold scheme(see Fig.1).

In order to facilitate the description of our scheme,suppose the minimal authorized set Aiis expressed as

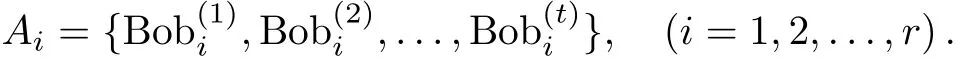
Step 1 Preparation:According to the authorized set Ai,the distributor Alice randomly chooses some numbers,and sendsto the participantthrough quantum secure direct communication.Note that ifappears in a different authorized set,Alice sends only one y(ν)i .

For the authorized set Ai,Alice generates two random numbersD and prepares a stateD and only Alice knows li,ji).Then she performs the operationand obtains a new signal state

Step 2 Distribution:Alice sends this stateto the fi rst participantin the authorized set Ai.After receiving the statehas not generated a private keythen he randomly chooses a numberOtherwise,the operation is skipped.Combined withsent by Alice,he performs the corresponding operationon this particle.sends the new statethe next participantin Ai.Thendoes the same operation asIn turn,the last participantin Aisends the new state to Alice until he follows the above method.

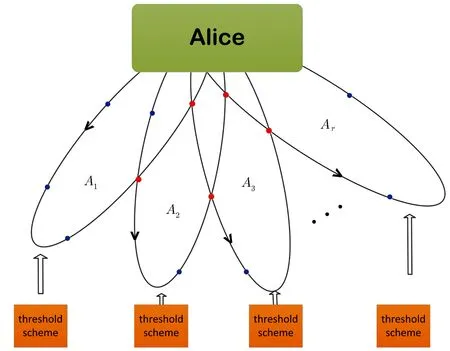
Fig.1 (Color online)A flow chart for the access structure Γ={A1,A2,...,Ar},where Ai(i=1,2,...,r)is the minimal authorized set.Blue and red dots represent all participants,where red dots indicate that participants appear in different minimal authorized sets.Arrows denote the direction of particle transport.Every minimal authorized set Aican be realized by a threshold scheme.

For authorized set Ai(i=1,2,...,r),the protocol works because after all the transformations the final state reads

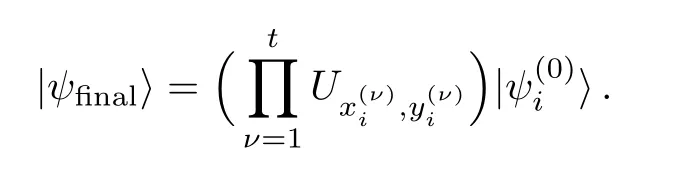
Step 3 Measurement:After Alice has received the signal state,she determines which basis to measure the particle according toThrough her calculation,if they satisfy the following condition

then she chooses theto make a measurement on the last particle and records the measurement result ai.It implies that the private data of all participants in the authorized setsatisfy globally consistency condition

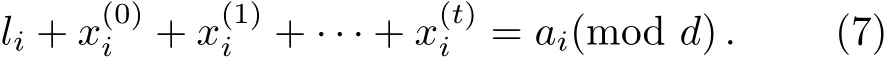
Step 4 Detection:In order to check the security,for a randomly chosen(by Alice)subset of the rounds,all participantsin Aisend their values of their private datato her,and Alice checks condition(7).If Eq.(7)does not hold,she aborts the scheme and starts again with a new set of resources.

Step 5 Reconstruction:If no eavesdropper is detected,according toand the measurement result ai,Alice can deduce that

For different authorized sets,there may be different bis.Therefore,Alice depends on bito adjust the parameter αi.In order to restore the original secret,each participant in Aisends the private keyto the trusted designed combiner(TDC).Afterwards,Alice also sends the parameter αiassociated with the authorized set Aito the TDC.After the TDC has received all data,it performs an operator O,which is denoted by

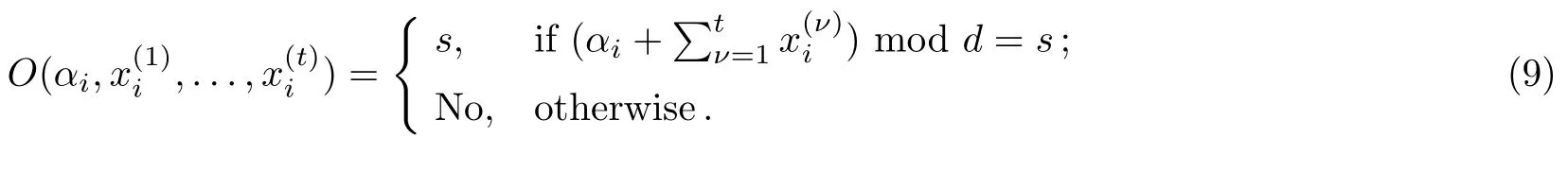
If Alice’s secret is more than one bit,Alice and all participants in the authorized set Aiexecute Steps 1–5 repeatedly.In order to save costs,the measurement basis information,can be reused.At the same time,Alice only needs to changeto ensure the security of every round.

Example 1 In order to explain our scheme more clearly,we will give an example in the following.Suppose the access structure is denoted by Γ={P1P4P5,P2P3P5,P1P2}with five honest participants and Alice wants to share the secret message s=2∈F5.We give a distributive flow chart for the access structure(see Fig.2).

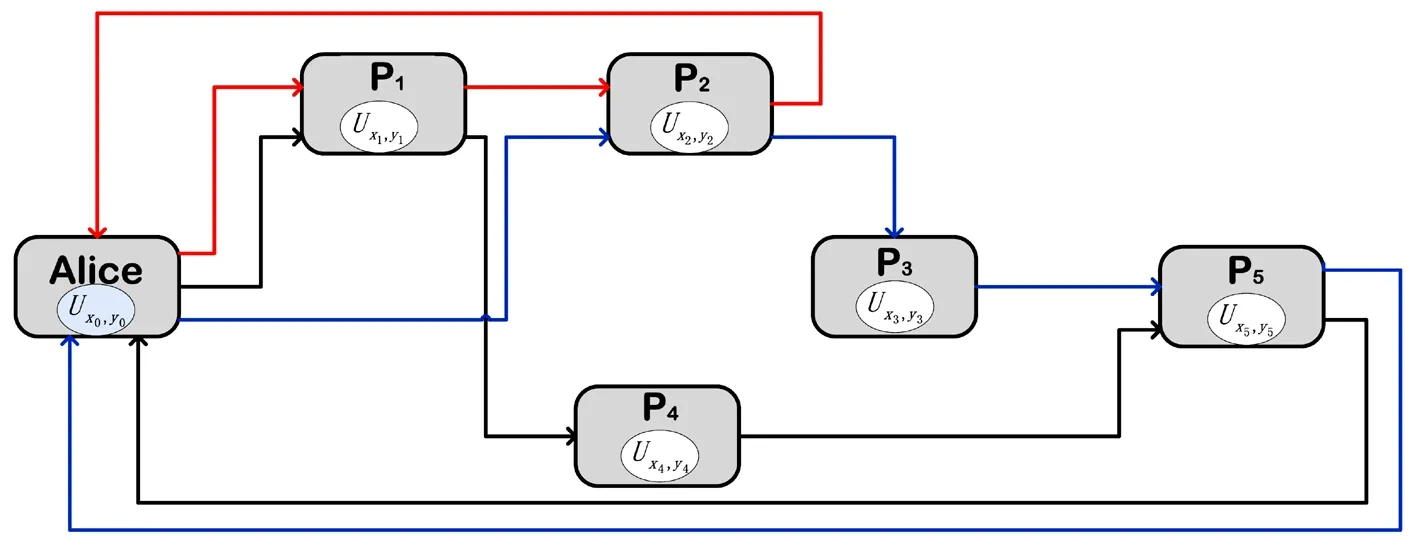
Fig.2 (Color online)A distributive flow chart for the access structure Γ={P1P2,P2P3P5,P1P4P5},where Ux,y represents everyone operation,the red line represents the authorized set P1P2,the blue line represents the authorized set P2P3P5and the black line represents the authorized set P1P4P5.

In accordance with the above steps all participants have their private keys.We assume that x1=0,x2=2,x3=3,x4=1,x5=3 respectively.

For the authorized set A1={P1P4P5},Alice can calculate that x1+x4+x5=4.Then she can choose parameter α1=3 and send it to the TDC.In order to restore the secret,P1,P4and P5send their private keys to the TDC.At last,the TDC can output the secret s=2(see Fig.3).

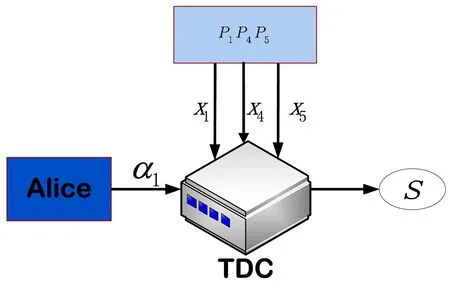
Fig.3 Reconstruction for the authorized set P1P4P5.

For the authorized set A2={P2P3P5},Alice can choose parameter α2=4 and send it to the TDC.P2,P3and P5send their private keys to the TDC.Then,the TDC can calculate α2+x2+x3+x5=12 mod 5=2 and output the secret s=2.

For the authorized set A3={P1P2},Alice can choose parameter α3=0.The TDC can calculate α3+x1+x2and output the secret.

4 Analysis of Our Scheme

4.1 Security Discussion

In Ref.[31],Tavakoli et al.have given the security analysis of their scheme.However,we have improved their scheme and implemented a general access structure using cascading method.In order to check the security of our scheme,we analyse the attacks of our scheme,i.e.external attack and internal attack.

External attack The first strategy for the eavesdropper Eve is the intercept-and-resend attack.For this attack,we consider two cases.

(a)Eve may intercept the qudit,in the stateon the way fromin the authorized set Ai.

(b)Eve may intercept the qudit sent by the distributor Alice and send a qudit of her own to the first participantin Aiin its stead.Eve collects her qudit once it is sent by the last participantin Ai.

However,for two cases,she does not have any information about the measurement basis becausein our protocol are sent to participants through quantum secure direct communication without publication.In order to get the original secret,she can only choose one of d relevant bases to measure.Obviously,Eve can obtain the correct measurement result only when she happens to choose the true basis j′=j.Therefore,the successful probability is 1/d.The eavesdropping,to some extent depending on d,causes inconsistencies between the private data and condition(7).In addition,if Alice sends n-bit secret,the successful probability to obtain information is(1/d)n.Thus when the numbers of n get larger,the probability is(1/d)n≈0.Therefore,this intercept-and-resend attack does not work in our scheme.

The second strategy for the eavesdropper Eve is the entangle-and-measure attack.Assuming that the eavesdropper Eve implements ancillary system to obtain the information.Suppose that Eve performs the unitary transform UEto entangle an auxiliary particle on the transmitted particle and then measures the auxiliary particle to steal secret information.Without loss of generality,we consider the basisin the following forms,

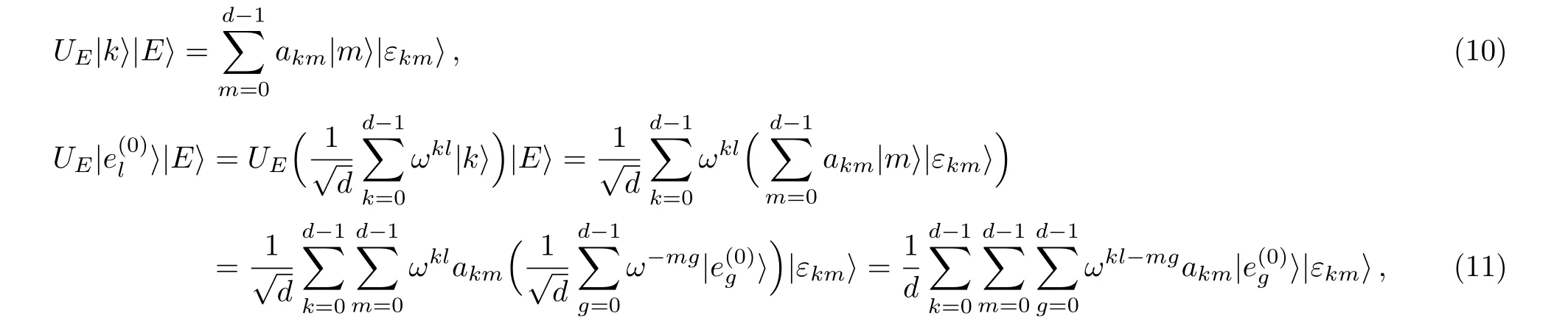
where ω =e2πi/d;|E⟩is the initial state of Eve’s ancillary system;|εkm⟩(k,m=0,1,...,d−1)is the pure auxiliary state determined uniquely by the unitary transform UE,and

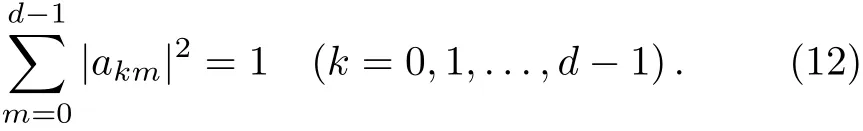
In order to avoid introducing the error rate,Eve has to set:akm=0,where km and k,m ∈ {0,1,...,d−1}.Therefore,Eq.(10)and Eq.(11)can be simplified as follows:

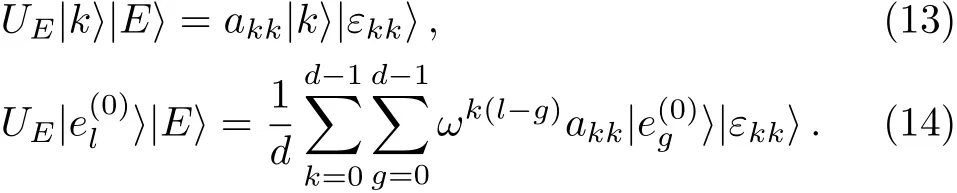
Similarly,Eve can obtain thatwhere g ∈ {0,1,...,d−1}and gl.Then for any l∈{0,1,...,d−1},we can get d equations.According to these d equations,we can compute that

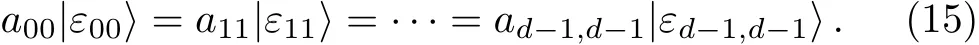
Therefore,no matter what the useful state is,Eve can only obtain the same information from ancillary particles.The similar discussion can be applied for the other quantum stateTherefore,the entangle-and-measure attack is unsuccessful.

In Ref.[31],the authors considered that an alternative attack used by Eve is to send via the unitary gate of playerone more qudit or even a multiqudit pulse so that it can be somehow intercepted by her beyond the gate without intercepting the protocol qudit.For the eavesdropping,it is not suitable for our scheme and she cannot learn the actual unitary transformation,becausein our protocol are not announced.

Internal attack In the following,we will primarily consider the participants conspiracy attack because it is always easier and more powerful than external attack and the participants can get more useful information than a fourth eavesdropper.In the worse case,only the distributor Alice and one more participant in each authorized set are honest.For example,we assume thatis honestand the rest t−1 are conspiring players.If they do not send their private keys to the TDC,they cannot recover any information because they do not know the TDC’s operator.If they send their private keys to the TDC,they can not restore the original information because the TDC does not start until it must receive all data.Even ifalso sends his key,they still can not obtain the secret due to the lack of Alice’s parameter αi.Because Alice’s parameter setting is dependent on the participant keys,if they send some fake keys,then the TDC will output “No”,that is,they cannot get the secret.

4.2 Comparision

In this section,we compare our protocol with Tavakoli’s scheme[31]in Table 1.

In Tavakoli’s scheme,all participants randomly choose the measurement basis information y1,...,yn,that is,the distributor Alice does not know any information about the measurement basis.Before announcing them,she randomly chooses the basis MJ={|e(J)x⟩|x∈D}(J∈D)to measure her own particle.Therefore,the probability of a valid round is 1/d.In addition,after y1,...,ynare announced,the eavesdropper may learn x1,...,xnfrom the attack with one more qudit or even a multiqudit pulse through the unitary gate.Therefore,the announcement of these data increases the probability of information leakage.In our protocol,the distributor voluntarily chooses y1,...,ynwithout announcement,that is,she knows the measurement basis information.Therefore,the probability of a valid round is 1.

In addition,Tavakoli et al. proposed an(n,n)-threshold scheme,i.e.,the(n,n)-threshold access structure.In our protocol,we give a quantum secret sharing scheme to realize a general access structure.If the access structure contains only one authorized set,then our scheme will become an(n,n)-threshold scheme.Therefore,our scheme is more extensive and meaningful.

Table 1 Comparison of Tavakoli’s scheme[31]and our proposed one.

5 Conclusion

In this paper,we proposed a quantum secret sharing scheme with a single d-level quantum state to realize a general access structure.In the proposed protocol,we still applied the cyclic property of MUBs because these bases are important tools in quantum information processing.In addition,we also analysed the security of our scheme against primary quantum attacks and compared our protocol with Tavakoli’s scheme.For our scheme,the probability of each valid round is 1.When our access structure contains only one authorized set,our scheme will be the same as Tavakoli’s.

However,since MUBs are still unknown,we only consider the odd primes.For even number or power of prime number,we do not give any discussion.In Refs.[36–27],many algebraic properties of power of prime numbers have been given,then we hope that more researchers will study these problems and propose more important schemes.

Acknowledgements

We want to express our gratitude to anonymous referees for their valuable and constructive comments.

[1]A.Shamir,Commun.ACM 22(1979)612.

[2]G.R.Blakley,in Proceedings of the National Computer Conference,(AFIPS,1979)(1979)pp.313–317.

[3]M.Hillery,V.Buzek,and A.Berthiaume,Phys.Rev.A 59(1999)1829.

[4]R.Cleve,D.Gottesman,and H.K.Lo,Phys.Rev.Lett.83(1999)648.

[5]D.Gottesman,Phys.Rev.A 61(2000)042311.

[6]F.G.Deng,H.Y.Zhou,and G.L.Long,J.Phys.A:Math.Gen.39(2006)14089.

[7]A.M.Lance,T.Symul,W.P.Bowen,et al.,Phys.Rev.Lett.92(2004)177903.

[8]F.G.Deng,X.H.Li,C.Y.Li,et al.,Phys.Rev.A 72(2005)044301.

[9]G.Gordon and G.Rigolin,Phys.Rev.A 73(2006)062316.

[10]W.K.Wootters and W.H.Zurek,Nature(London)299(1982)802.

[11]D.Dieks,Phys.Lett.A 92(1982)271.

[12]A.Karlsson,M.Koashi,and N.Imoto,Phys.Rev.A 59(1999)162.

[13]L.Xiao,G.L.Long,F.G.Deng,and J.W.Pan,Phys.Rev.A 69(2004)052307.

[14]H.Cao and W.P.Ma,IEEE Photonics J.9(2017)1.

[15]C.M.Bai,Z.H.Li,T.T.Xu,and Y.M.Li,Int.J.Theor.Phys.55(2016)4972.

[16]A.Maitra,S.J.De,G.Paul,and A.K.Pal,Phys.Rev.A 92(2015)022305.

[17]L.H.Gong,H.C.Song,C.S.He,et al.,Physica Scripta 89(2014)035101.

[18]P.Sarvepalli and R.Raussendorf,Phys.Rev.A 81(2010)052333.

[19]L.Y.Hsu and C.M.Li,Phys.Rev.A 71(2005)022321.

[20]C.M.Bai,Z.H.Li,M.M.Si,et al.,Eur.Phys.J.D 71(2017)255.

[21]X.J.Wang,L.X.An,X.T.Yu,et al.,Phys.Lett.A 381(2017)3282.

[22]Y.F.He and W.P.Ma,Int.J.Quantum Inf.14(2016)1650007.

[23]K.J.Zhang,L.Zhang,T.T.Song,et al.,Science China Phys.Mech.&Astron.6(2016)1.

[24]Z.Zhang,W.Liu,and C.Li,Chin.Phys.B 20(2011)050309.

[25]R.Rahaman and M.G.Parker,Phys.Rev.A 91(2015)022330.

[26]Y.H.Yang,F.Gao,X.Wu,et al.,Sci.Rep.5(2015)16967.

[27]C.M.Bai,Z.H.Li,T.T.Xu,et al.,Quantum Inf.Process 16(2017)59.

[28]J.Wang,L.Li,H.Peng,and Y.Yang,Phys.Rev.A 95(2017)022320.

[29]J.T.Wang,G.Xu,X.B.Chen,et al.,Phys.Lett.A 381(2017)998.

[30]H.Lu,Z.Zhang,L.K.Chen,et al.,Phys.Rev.Lett.117(2016)030501.

[31]A.Tavakoli,I.Herbauts,M.Zukowski,and M.Bourennane,Phys.Rev.A 92(2015)030302(R).

[32]V.Karimipour and M.Asoudeh,Phys.Rev.A 92(2015)030301(R).

[33]S.Lin,G.D.Guo,Y.Z.Xu,et al.,Phys.Rev.A 93(2016)062343.

[34]C.Lu,F.Miao,et al.,Quantum Inf.Process 17(2018)64.

[35]C.Wang,F.Miao,Y.S.Li,et al.,Phys.Rev.A 71(2005)044305.

[36]I.D.Ivonovic,J.Phys.A:Math.Gen.14(1981)3241.

[37]W.K.Wootters and B.D.Fields,Ann.Phys.191(1989)363.