Exhaustive Classification of the Invariant Solutions for a Specific Nonlinear Model Describing Near Planar and Marginally Long-Wave Unstable Interfaces for Phase Transition
2018-06-11FatemehAhangari
Fatemeh Ahangari
Department of Mathematics,Faculty of Mathematical Sciences,Alzahra University,Tehran,P.O.Box 1993893973,Iran
1 Introduction
The term phase transition or phase change is most frequently applied in order to explain transitions among liquid,solid and gaseous states of matter and,in infrequent cases,plasma physics.A phase of a thermodynamic system and the states of substance have identical physical characteristics.During a phase transition of an arbitrary medium specific properties of the medium alter,as a consequence of some external condition,such as pressure,temperature,or others.The quantification of the associated external conditions at which transformation happens is denoted by phase transition.Problems of thermodynamic phase transition are considerably common in nature and applied today in many technologies such as solidification and combustion.The dynamics can be modeled by an interface motion whenever the transition region between two locally stable phases is narrow enough.Reducing the PDEs determining the constituents in each phase to a straightforward equation of motion for an interface can be regarded as one of the constructive procedures of attack for these problems.Particularly,if the system is isotropic,it is practicable to suppose that the normal velocity of the interface relies on only local geometrical characteristics such as curvature.In other words,the purely local coupling between points on the interface and isotropy of the system imply that the velocity of the interface is totally determined via local geometric properties of the interface such as the mean and Gaussian curvature.In the early 1980s such an intrinsic equation of motion to model solidification was introduced by Langer[1−2]and Brower et al.[3−4]
The smallness of the scale of variation of the constituents transverse to the interface compared to the characteristic scale of variation along the interface,can be reckoned the fundamental assumption that enables a reduction to interface dynamics.The mentioned ratio is denoted by ε,for small ε a perturbation expansion for the normal velocity of the interface,V is attained as follows:

In Eq.(1)K indicates the mean curvature,Q is the Gaussian curvature,µ,ν,α,β,γ are constants resulted from the perturbation expansions andis the surface Laplacian.It is worth mentioning that at order εnthe contribution to the velocity scales like(length)−nand that the terms arising can be regarded as the isotropic characterizations of the local geometry of the surface.[5]
Note that in the special case that curvature is marginally destabilizing(ν <0,|ν|≤ 1),this term can be asymptotically balanced with higher stabilizing terms in the expansion of the normal velocity.Particularly,shortwave perturbations to planar interfaces are damped whenever γ<0.This observation motivated Sivashinsky and Frankel to derive Eq.(1)in the context of combustion.[6−8]Moreover,the same equation also appears in order to describe the motion of an interface in multicomponent bistable reaction/diffusion equations.In addition,in the context of solidification of a hypercooled melt,the iden-tical equation was obtained in Refs.[6,9–11](refer to Ref.[5]for more details).
Frankel[6,9]demonstrated that when the curvature term is marginally destabilizing,for near planar solutions the intrinsic equation of motion reduces to the well known Kuramoto-Sivashinsky(KS)equation.Bern off and Bertozzi[5]by considering the near planar case when both µ and ν may be small,could derive an amplitude equation,which is more general.In Ref.[5]according to Sarocka and Berno ff,[10]the location of the interface is denoted byTaking into account the declared coordinate system,V,K,Q,andatisfy the following identities:

Here∇ and∇2indicate derivatives with respect to the(,)coordinates.By rescaling the coordinates the leading order terms are balanced as follows:
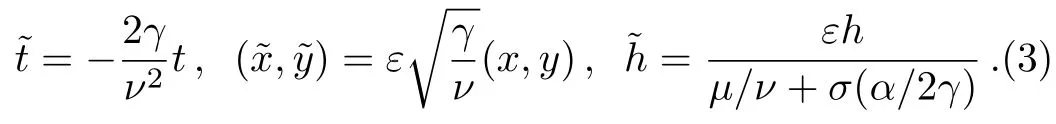
Consequently,the two-dimensional modified Kuramoto-Sivashinsky(2D)MKS equation is derived:
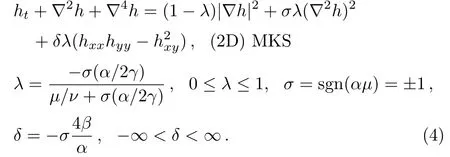
Note that this rescaling is reasonable in the limit|ν|−→ 0.In particular,if|ν|≪ µ that λ −→ 0 recovers the standard Kuramoto-Sivashinsky(KS)equation.The KS equation has been originally derived in the context of chemical turbulence[12]and is of special significance mainly due to the fact that it can describe the flow of a falling fluid film.[13]The solutions of the KS equation can clarify the features about the evolution of surface morphology,which is instructive to the investigations of the mechanism of thin film growth.Furthermore,in the near planar theory((2D)MKS equation)the eminent limit of both µ and ν tending to zero,whenever(µ/ν)∼ O(1),results the terms,which are proportional to(∇2h)2and hxxhyy−h2xy;the mentioned terms are respectively attained from the K2and Q terms in the intrinsic equation of motion(1).
Some important results concerning the KS equation are already known.For example,fractal tracer distributions of particles advected in the velocity field of the KS equation was found in Ref.[14].Qi et al.in Ref.[15]have studied the evolution of(2+1)-dimensional surface morphology in the Kuramoto-Sivashinsky(KS)model by using the numerical simulation approach.In Ref.[16],we have presented a complete study of classical and nonclassical symmetries of the damped version of the two dimensional KS equation.
In this paper,an exhaustive analysis of the invariant solutions for the(2D)MKS equation(4)is presented.The investigation of the solutions of nonlinear evolution equations has a fundamental role in the nonlinear physical phenomena.The most famous and established method in order to attaining special solutions of systems of nonlinear differential equations(PDEs)is the classical symmetries method,also called Lie group analysis,which originated at the end of nineteenth century from the pioneering work of Lie.[17]He illustrated that the problem of attaining the Lie group of point transformations leaving invariant an arbitrary differential equation(ordinary or partial)namely a point symmetry of a differential equation reduced to solving related linear systems of determining equations for its infinitesimal generators.Lie also demonstrated that in the case of an ODE,regardless of any imposed initial conditions,a point symmetry of a differential equation leads to reduction of the order and,in the case of a PDE,to obtaining specific solutions called invariant(similarity)solutions.Furthermore,he indicated that a point symmetry of a differential equation generates a one-parameter family of solutions from any known solution of a differential equation that is not an invariant solution originating from the symmetry.Most importantly,Lie’s work are considerably applicable to nonlinear DEs.Lie’s constructive researches are comprehensively discussed in Refs.[18–23]as well as many other outstanding references therein.Nowadays,application of Lie symmetry method for constructing the solutions of nonlinear partial differential equations(PDEs)can be regarded as one of the most important and active fields of research in the theory of nonlinear PDEs and applications(refer to Refs.[24–29]).
The fact that symmetry reductions for many PDEs can not be obtained via the classical symmetry method,was the motivation to create several generalizations of the classical Lie group method for symmetry reductions.One of the most significant extensions relates to Lie’s work on obtainig invariant solutions for PDE systems.As declared above,a point symmetry of a PDE system maps each of its solutions into a one-parameter family of solutions.But some solutions map into themselves,in other words,they are themselves invariant.This kind of solutions satisfy the characteristic PDE determined by the invariant surface condition providing the invariants of the point symmetry.Moreover,the invariant solutions emerging from the point symmetry are the solutions of the given PDE system that satisfy the augmented system including this characteristic PDE with known coefficients,which are attained from the point symmetry together with the given PDE system itself.Thus the invariant solutions are resulted as solutions of a reduced system with one less independent variable.This procedure(Lie’s classical method)to obtain invariant solutions of a given PDE is generalized by the non-classical method introduced in Bluman’s 1967 PhD thesis where one looks for solutions of an augmented system comprising the given PDE system and the characteristic PDE with unknown coefficients in addition to differential consequences of the augmented system.Ultimately,via substituting the characteristic equation and its corresponding differential consequences,into the determining system for point symmetries of the augmented system the unknown coefficients are achieved.It is noticeable that the obtained over-determined system is nonlinear in these unknown coefficients.However,it is less over-determined than is the case when acquiring point symmetries of the given PDE system.Therewith,each solution of the determining system in the case of point symmetries is precisely a solution of the determining system for the unknown coefficients of the characteristic PDE.Consequently,solving for the unknown coefficients,the associated non-classical solutions of the augmented system are determined,which by construction comprise the classical invariant solutions.
This paper is organized as follows:In Sec.2,by applying the basic Lie symmetry method the most general Lie point symmetry group of the(2D)MKS equation is determined.Also,some results deduced from the structure of the Lie algebra of symmetries are presented and the associated one-parameter subgroups and the most general group-invariant solutions are obtained.Section 3 is devoted to comprehensive classification of symmetry subalgebras for the(2D)MKS equation.The Lie invariants and similarity reduced equations corresponding to the infinitesimal symmetries of the(2D)MKS equation are obtained in Sec.4.Section 5 is dedicated to the investigation of the nonclassical symmetries of the(2D)MKS model,symmetries generated when a supplementary condition,i.e.the invariant surface condition,is imposed.Some concluding remarks are presented at the end of the paper.
2 Computation of the Classical Symmetries for the(2D)MKS Equation
From the topological point of view,a continues symmetry of a PDE system can be regarded as a transformation,which leaves the solution manifold of the system invariant.In other words,this transformation maps(deforms)any solution of the system into a solution of the identical system.But practically computation of the continuous symmetries of a given system of PDEs is limited to investigate symmetries,which are local transformations acting on its space of independent variables,dependent variables and their corresponding derivatives.Lie’s algorithm to obtain Lie point symmetries is thoroughly presented in Refs.[18,20–23].Lie point symmetries are resulted from solutions of linear systems of determining equations associated to components of infinitesimal generators for the independent and dependent variables of a given PDE system.Meanwhile,the mentioned components themselves depend only on the independent and dependent variables of the given PDE system.Moreover it is worth mentioning that point transformations,which are operating on the space of the dependent and independent variables of a given PDE system can be appropriately prolonged to point transformations operating on the space of the given dependent variables,independent variables and their derivatives to any finite order.
Consider a system E{x;u}consisting of N PDEs of order k with n independent variable x=(x1,...,xn)and m dependent variables u(x)=(u1(x),...,um(x)),defined by:
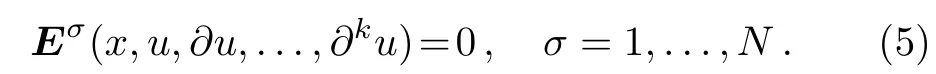
Partial derivatives are denoted by= ∂uµ(x)/∂xi;the set of all first-order partial derivatives is denoted by the following notation:
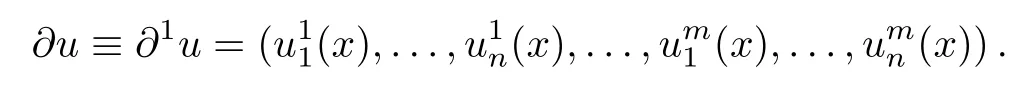
Moreover,the set of all partial derivatives of order p is given by:

The total derivative operators are defined as follows:
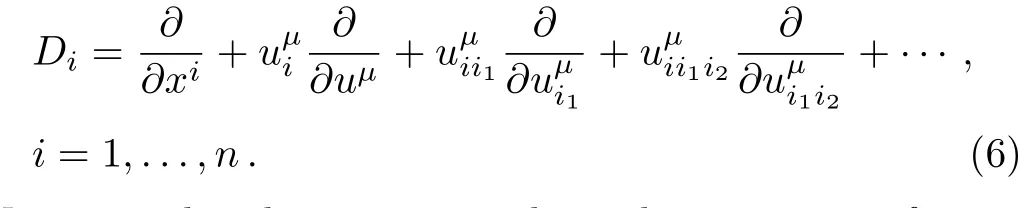
Now consider the situation where the point transformations is a one-parameter Lie group of point transformations given by
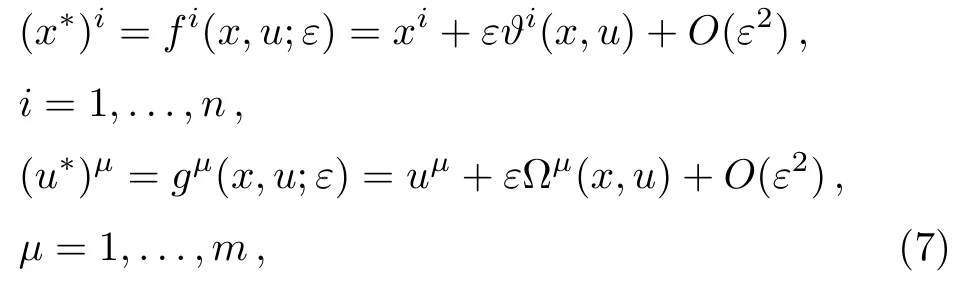
with the infinitesimal generator given by
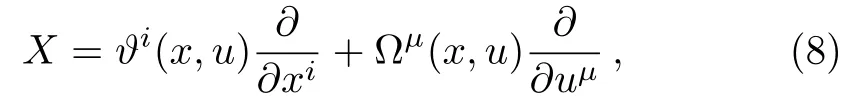
or equivalently,in evolutionary form
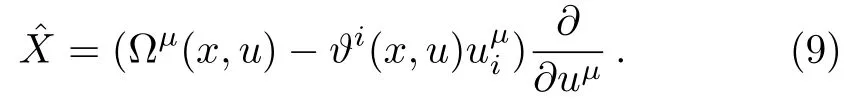
A one-parameter Lie group of point transformations(7)induces the following one-parameter Lie group of point transformations,which is acting on (x,u,∂u)-space,...,(x,u,∂u,...,∂ku)-space
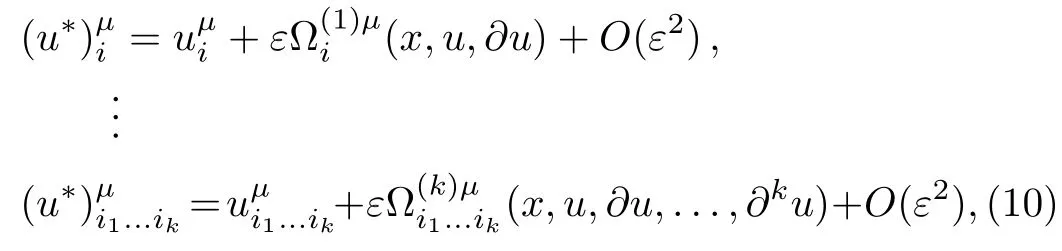
with the extended infinitesimals given by
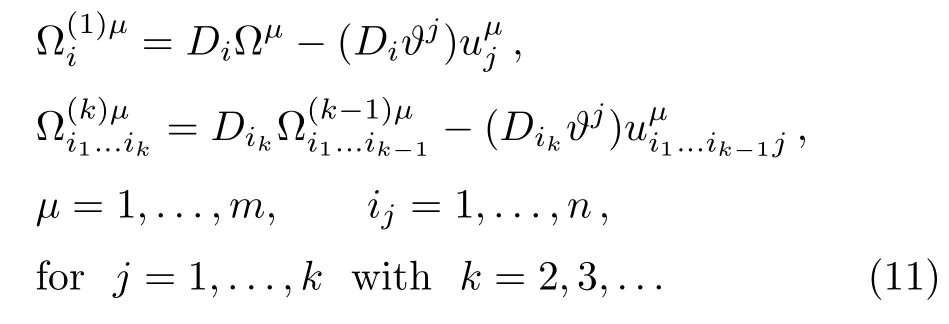
The k-th extended infinitesimal generator(k-th prolongation of Eq.(8))is given by
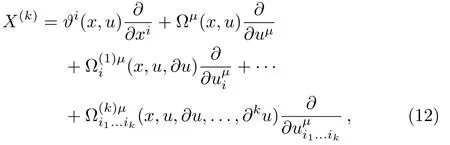
whereare defined in terms of{ϑi(x,u),Ωµ(x,u)}by Eq.(11).
A one-parameter Lie group of point transformations(7)leaves the PDE system E{x;u}(5)invariant if and only if its k-th prolongation(12)leaves invariant the solution manifold of E{x;u}in(x,u,∂u,...,∂ku)-space.In other words,any family of solution surfaces of the PDE system(5)is mapped into another family of solution surfaces of PDE system(5)via this transformation.In this case,the one-parameter Lie group of point transformations(7)is called a point symmetry of the PDE system E{x;u}(5).Lie’s outstanding algorithm to obtain the point symmetries of a given PDE system(5)can be generally expressed as follows:
Let Eq.(8)be the infinitesimal generator of a oneparameter Lie group of point transformations(7)and assume that Eq.(12)is its k-th prolongation.Then the transformation(7)is a point symmetry of the PDE system E{x;u}(5)if and only if
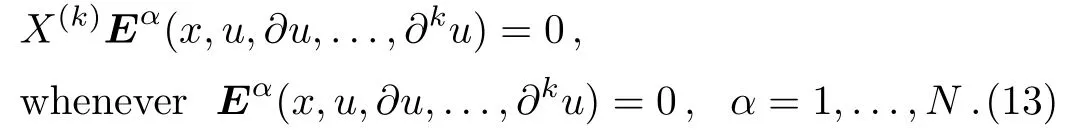
It is noticeable that the invariance criterion(13)involves substitutions of the given N PDEs and possibly their corresponding differential consequences into each of the N determining equations(13).The resulting linear system to compute the components ϑi(x,u), Ωµ(x,u)of the infinitesimal generator(8)is denoted by the set{ of determining equations for the point symmetries of Ex;u}(5).
Moreover,in the resulting set of determining equations for the point symmetries of E{x;u},each uµand each of its corresponding derivativesetc.can be properly treated as independent variables along with xi.As a main consequence,the set of determining equations properly splits into an overdetermined linear PDE system for{ϑi(x,u),Ωµ(x,u)}.In addition,whenever the number of generators is finite,the number of arbitrary constants that appear in the solution of the set of determining equations is precisely the number of point symmetry generators(8).Ultimately,after the symmetry components{ϑi(x,u),Ωµ(x,u)},(i=1,...,n; µ =1,...,m)are totally determined,the global form of the Lie group of point transformations can be obtained through either solving a corresponding system of first-order ODEs or exponentiation in terms of the infinitesimal point symmetry generators.For more complete details refer to Refs.[18–23].
Now we will perform the Lie group method for Eq.(4).Firstly,let us consider the following one-parameter Lie group of infinitesimal transformation:

with a small parameter ε≪ 1.The symmetry generator associated with the above group of transformations can be written as:

The fourth prolongation of X is the vector field
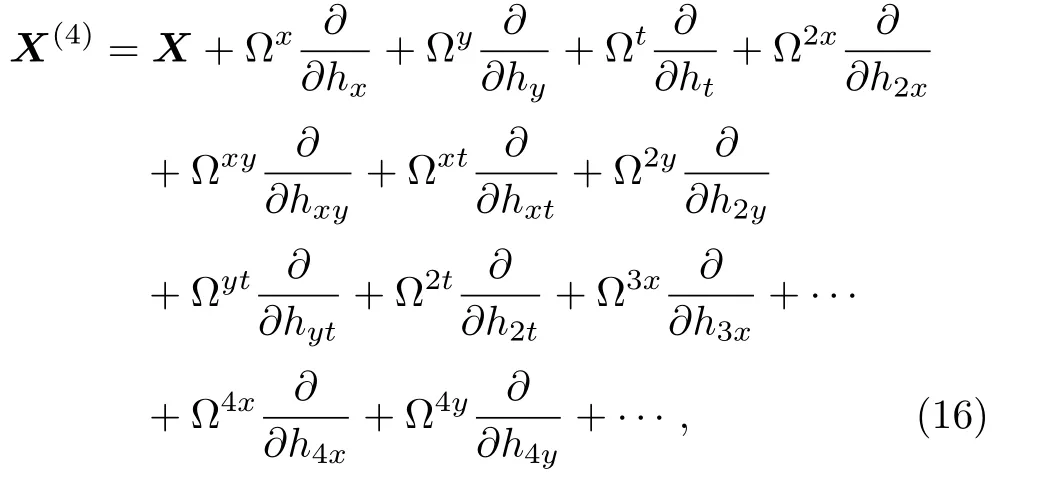
with coefficients
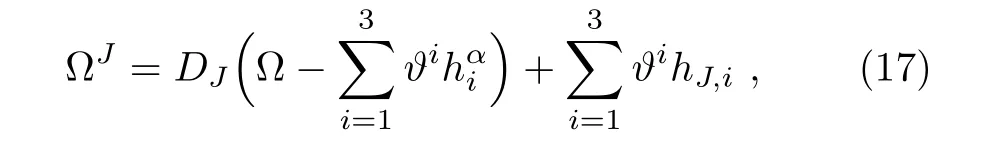
where J=(i1,...,ik),1≤ik≤3,1≤k≤4,and the sum is over all J’s of order 0<#J ≤ 4.
Taking into account(13)the invariance condition for the(2D)MKS equation(4)is given by the relation:
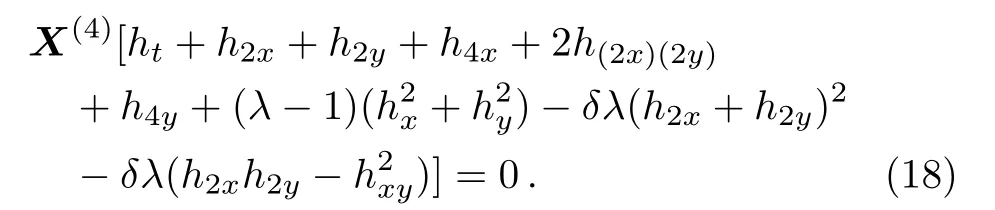
The invariance condition(18)is equivalent with the following equation:
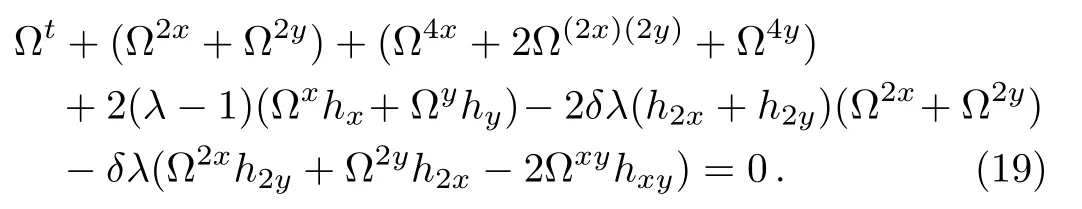
Substituting Eq.(17)into invariance condition(19),we are left with a polynomial equation involving the various derivatives of h(x,y,t)whose coefficients are certain derivatives of ϑ1,ϑ2,ϑ3and Ω.Since,ϑ1,ϑ2,ϑ3and Ω depend only on x,y,t,h,we can equate the individual coefficients to zero,leading to the following complete set of determining equations:
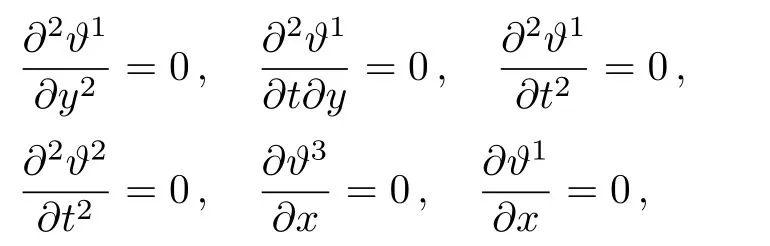
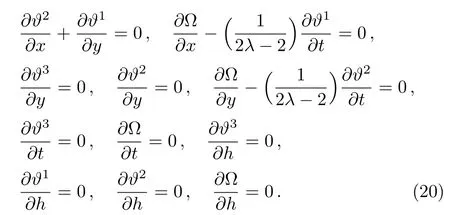
By solving this system of PDEs,we find that:
Theorem 1 The Lie group of point symmetries of(2D)MKS equation(4)has a Lie algebra generated by the vector fields
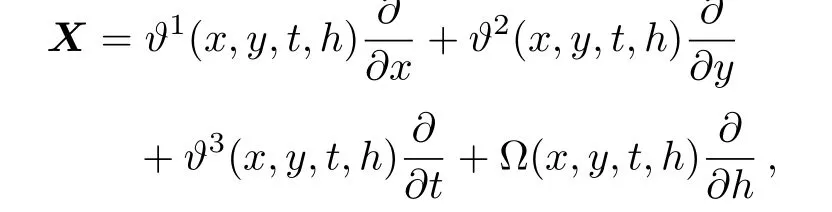
where
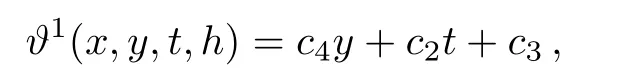
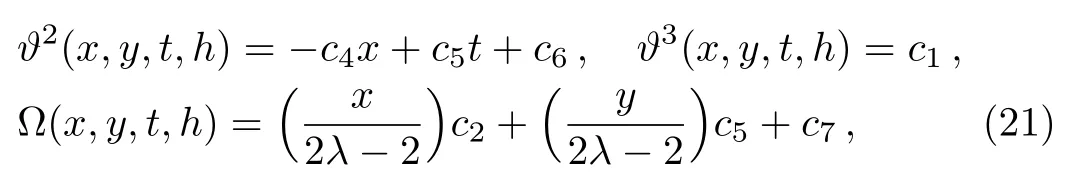
and ci,i=1,...,7 are arbitrary constants.
Corollary 1 infinitesimal generators of every one parameter Lie group of point symmetries of the(2D)MKS equation(4)are as follows:
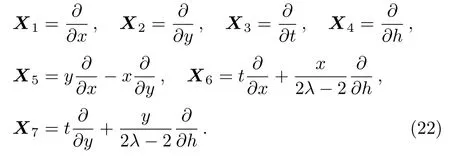
The commutator table of symmetry generators of the MKSE is given in Table 1,where the entry in the i-th row and j-th column is defined as[Xi,Xj]=XiXj−XjXi,i,j=1,...,7. ?
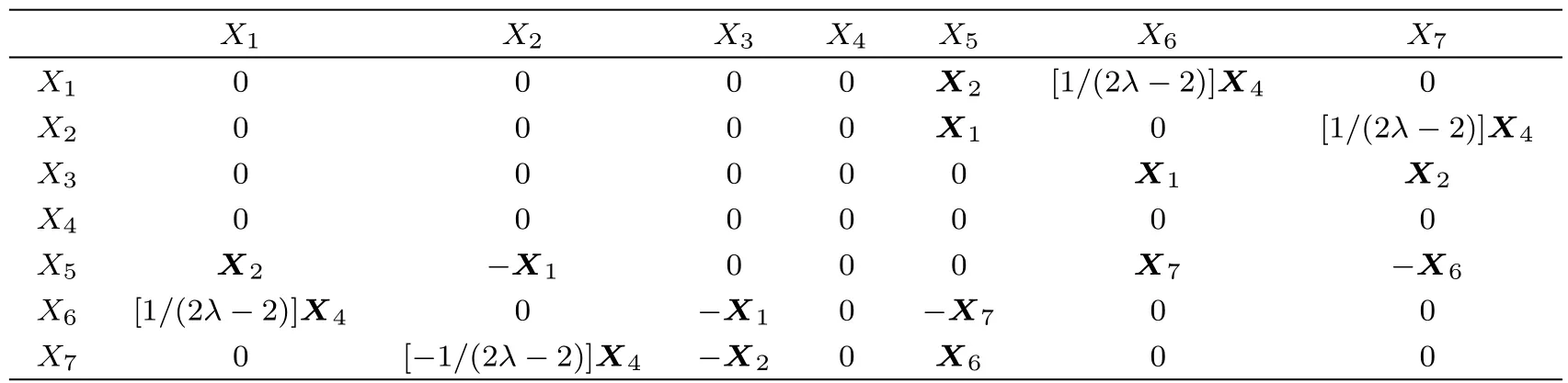
Table 1 Commutation relations satisfied by infinitesimal generators.
2.1 The Structure of the Lie Algebra of Symmetries
In this part,we briefly discuss the structure of symmetry Lie algebra of the(2D)MKS equation(4),which is denoted by g.
Firstly,it is worth mentioning that g has no non-trivial Levi decomposition in the form g=r×g1,because g has not any non-trivial radical,i.e.if r be the radical of g,then g=r.
Furthermore,the Lie algebra g is solvable and nonsemisimple.It is solvable,because if
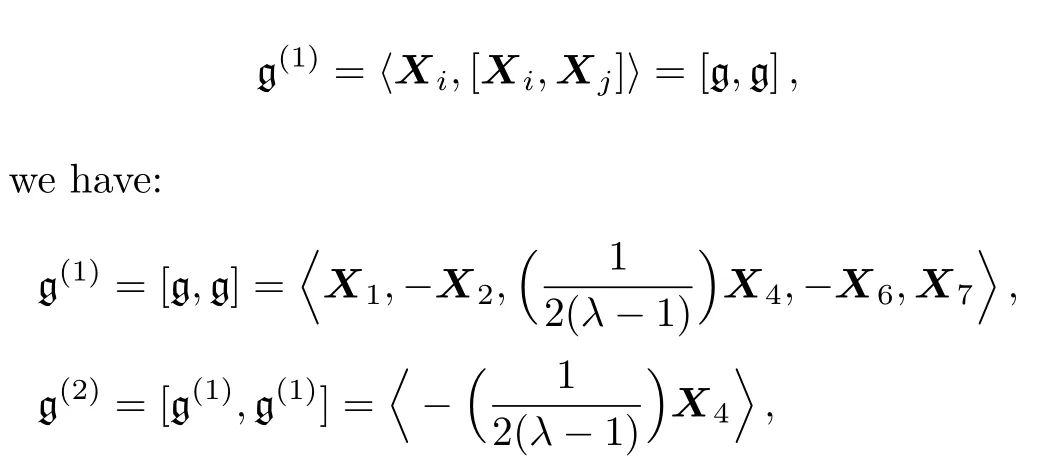
so we have the following chain of ideals g(1)⊃g(2)⊃{0}.
Also,g is not semisimple,because its killing form
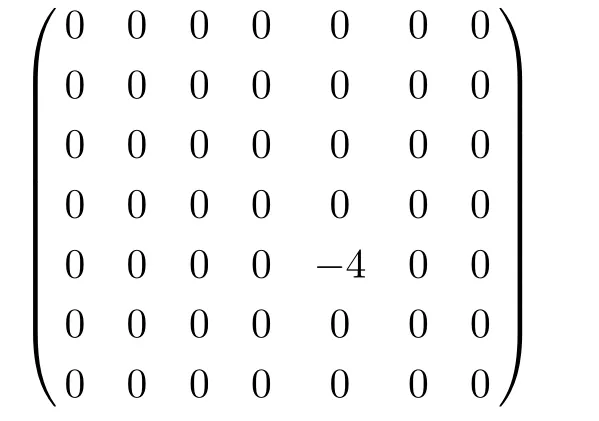
is degenerate.
Taking into account the table of commutators,g has two abelian four and two-dimensional subalgebras,which are spanned by ⟨X1,X2,X3,X4⟩and ⟨X6,X7⟩,respectively,such that the first one is an ideal in g.
2.2 Symmetry Transformations and Group Invariant Solutions of the(2D)MKS Equation
The equation(4)can be considered as a submanifold of the jet space J4(R3,R).Hence,the most general group invariant solutions of the(2D)MKS equation(4)can be obtained.In order to determine the group transformation,which is generated by the infinitesimal generatorsit is necessary to solve the following seven systems of first order ordinary differential equations
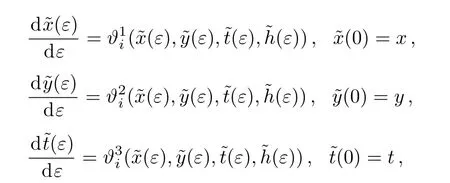
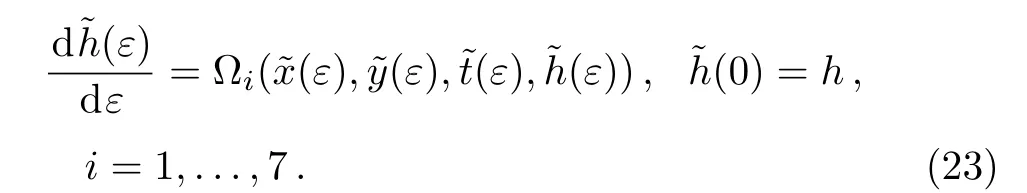
Hence,the one parameter groups Gk(ε)generated by Xkfor k=1,...,7,can be obtained by exponentiating the infinitesimal symmetries of Eq.(4).
Theorem 2 The one-parameter groups Gi(ε):M −→ M generated by the Xi,i=1,...,7,are given as follows:
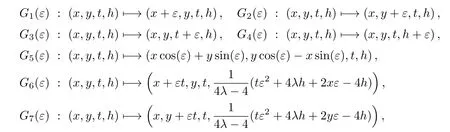
where entries give the transformed point exp
These operators,which generate invariance of the evolution equation(4),correspond to the following transformations:G1and G2are spatial translations,G3generates temporal translation,G4is a gauge transformation,G5is a spatial rotation and G6and G7demonstrate Galilean boosts.
Taking into account the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,the following theorem can be stated:Theorem 3 If H=h(x,y,t)is a solution of equation(4),so are the following functions
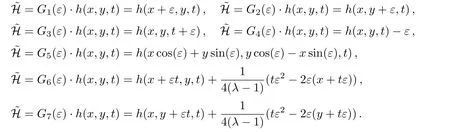
Now,the general group of symmetries can be obtained by considering a general linear combination γ1X1+···+γ7X7of the given vector fields.Particularly,if G is the action of the symmetry group near identity,it can be represented in the form G=exp(ε7X7)o···oexp(ε1X1).Consequently,from above theorem we can state that:
Corollary 2 For the arbitrary combination of infinitesimal symmetry generators of the formthe(2D)MKS equation(4)has the following solution
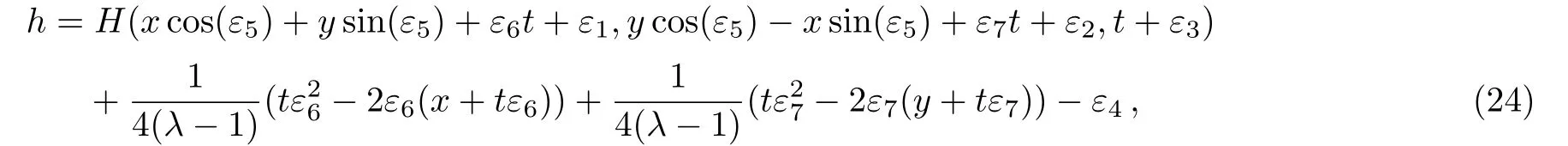
where εi,i=1,...,7 are arbitrary real numbers.
3 Comprehensive Classification of Subalgebras for the(2D)MKS Equation
One of the significant extensions associates with Lie’s researches on obtaining invariant solutions for PDE systems.As declared previously,from the topological point of view a point symmetry of an arbitrary PDE system maps(deforms)each of its solutions into a one-parameter family of solutions.But the considerable fact is that some solutions map into themselves,in other words,they are themselves invariant.These kind of solutions satisfy the characteristic PDE,which is defined by the invariant surface condition resulting the invariants of the point symmetry.Consequently,the invariant solutions,which are determined via the point symmetry can be regarded as the solutions of the given PDE system,which satisfy the extended system comprising this characteristic PDE with known coefficients that resulted from the corresponding point symmetry and the given PDE system itself.Furthermore,the invariant solutions can be considered as solutions of a reduced system with one less independent variable.Taking into account the fact that any linear combination of infinitesimal generators is also an infinitesimal generator,there are always infinitely many distinct symmetry subgroups for the differential equation.As a consequence,in order to thorough characterization of the invariant solutions,a procedure of determining,which subgroups would yield essentially different types of solutions is inevitable and significant.
Since any transformation in the full symmetry group maps a solution to another solution,it is enough to obtain those invariant solutions,which are not related by transformations in the full symmetry group,this has led to the notion of an optimal system.[22]The problem of determining an optimal system of subgroups is equivalent to that of obtaining an optimal system of subalgebras.For one-dimensional subalgebras,this classification problem is precisely the same as the problem of classifying the orbits of the adjoint representation.The mentioned purpose can be completely accomplished by selecting a general element in the Lie algebra and subjecting it to various adjoint transformations so as to simplify it as much as possible.Hence,constructing an optimal system of a Lie algebra is equivalent to attain different invariant solutions,which are not essentially in a same orbit of adjoint actions.
As a result,this means that the problem of obtaining invariant solutions under a group action G or its subgroups is reduced to problem of constructing optimal system of its corresponding subalgebras.Therefore,whenever the optimal system of subalgebras is attained,this optimality yields the smallest subspace in the set of solutions possessing the following property:Any invariant solution,which can be resulted from any subgroup of G is located in one of the orbit of G-action,i.e.optimal system.In Ref.[25]a direct algorithm of one-dimensional optimal system for group invariant solutions is discussed.In addition,in Ref.[28]a Maple package for generating one-dimensional finite Lie algebra is proposed.Also,the procedures of constructing two-dimensional optimal system of the group invariant solutions are comprehensively investigated in Ref.[26].
Let E{x;u}be an arbitrary system of differential equations admitting the symmetry Lie group G.Now G operates on the set of solutions S of E{x;u}.Let s·G be the orbit of s,and H be a subgroup of G. Invariant H-solutions s∈S are distinguished by equality s·S={s}.If h∈G is a transformation and s∈S,then h ·(s·H)=(h ·s)·(hHh−1).Consequently,according to Ref.[20]every invariant H-solution s transforms into an invariant hHh−1-solution.Thus different invariant solutions are resulted from similar subgroups of G.So,classification of invariant H-solutions is reduced to the problem of classification of subgroups of G,up to similarity.An optimal system of s-dimensional subgroups of G is a list of conjugacy inequivalent s-dimensional subgroups of G with the property that any other subgroup is conjugate to precisely one subgroup in the list.Similarly,a list of s-dimensional subalgebras forms an optimal system if every s-dimensional subalgebra of g is equivalent to a unique member of the list under some element of the adjoint representation:=Ad(g)·h.
Let H andbe connected,s-dimensional Lie subgroups of the Lie group G with corresponding Lie subalgebras h andof the Lie algebra g of G.Then=gHg−1are conjugate subgroups if and only=Ad(g) ·h are conjugate subalgebras.[20,22]Consequently,the problem of obtaining an optimal system of subgroups is equivalent to that of finding an optimal system of subalgebras.So,we concentrate on this issue in the following.
3.1 Optimal System of One-Dimensional Subalgebras of the(2D)MKS Equation
There is clearly an in fi nite number of one-dimensional subalgebras of the(2D)MKS equation(4)Lie algebra,g,each of which may be applied to construct a special solutions or class of solutions.So,it is impossible to use all the one-dimensional subalgebras of the(2D)MKS equation to construct invariant solutions.However,a well known standard procedure[20,22]allows us to classify all the one-dimensional subalgebras into subsets of conjugate subalgebras.This involves constructing the adjoint representation group,which introduces a conjugate relation in the set of all one-dimensional subalgebras.In fact for one-dimensional subalgebras,the classification problem is precisely the same as the problem of classifying the orbits of the adjoint representation.If we select only one representative from each family of equivalent subalgebras,an optimal set of subalgebras is created.The corresponding set of invariant solutions is then the minimal list from which we can get all other invariant solutions of one-dimensional subalgebras simply via transformations.
Each Xi,i=1,...,7,of the basis symmetries generates an adjoint representation(or interior automorphism)Ad(exp(εXi))defined by the Lie series
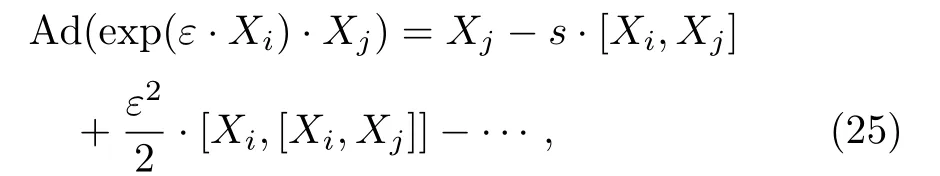
where[Xi,Xj]is the commutator for the Lie algebra,s is a parameter,and i,j=1,...,7. In Table 2 we give all the adjoint representations of the(2D)MKS equation Lie group,with the(i,j)the entry indicating Ad(exp(εXi))Xj.Fundamentally,these adjoint representations simply permute amongst similar one-dimensional subalgebras.Hence,they are effectively applied in order to identify similar one-dimensional subalgebras.
We can expect to simplify a given arbitrary element,
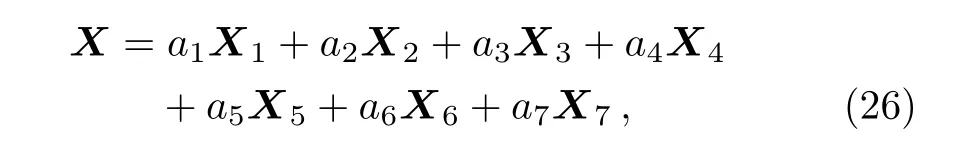
of the(2D)MKS equation Lie algebra g. Note that the elements of g can be represented by vectors a=(a1,...,a7)∈R7since each of them can be written in the form(26)for some constants a1,...,a7.Hence,the adjoint action can be regarded as(in fact is)a group of linear transformations of the vectors(a1,...,a7).

Table 2 Adjoint representation generated by the basis symmetries of the(2D)MKSE Lie algebra.
Therefore,we can state the following theorem:
Theorem 4 The one-dimensional optimal system of the(2D)MKS equation Lie algebra g is given by
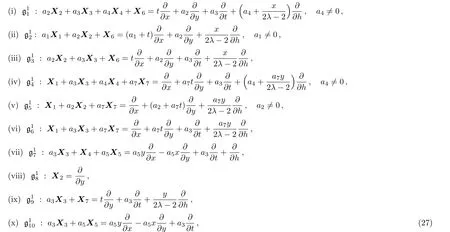
where ai,i=1,...,7 are arbitrary real numbers.
Proofdefined by X 7→ Ad(exp(siXi)·X)is a linear map,for i=1,...,7.The matrixofi=1,...,7,with respect to basis{X1,...,X7}is
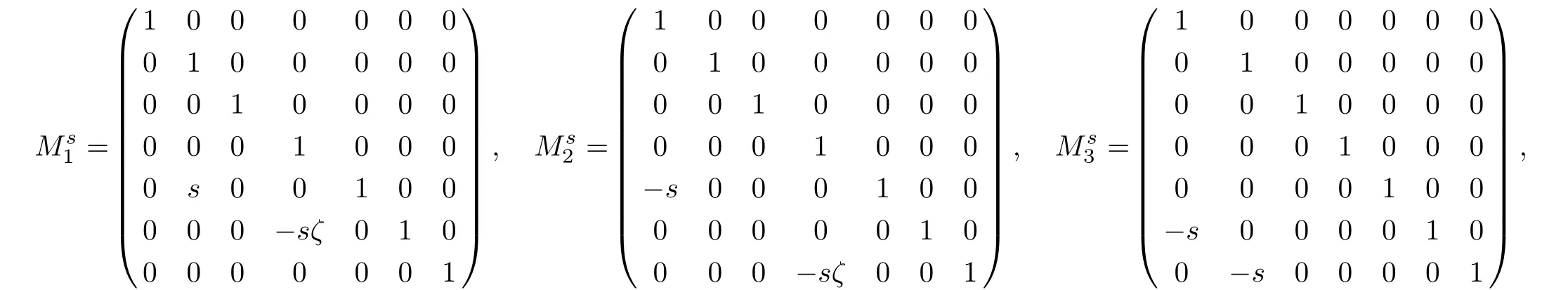

respectively,where S=sins,C=coss and ζ=1/(2λ −2).then
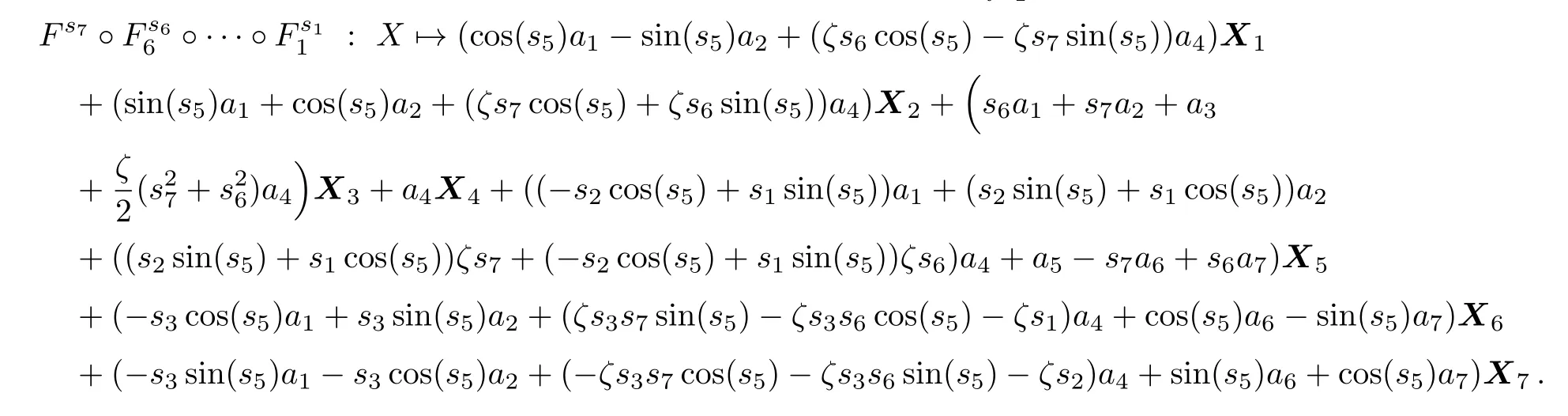
Now,we can simplify X as follows:
If a60 and a40 we can make the coefficients of X1,X5and X7vanish byBy setting s5= −arctan(a7/a6),s6= −a1/ζa4and s7=a5/a6,respectively.Scaling X if necessary,we can assume that a6=1.So,X is reduced to the case(i).
If a60,a4=0 and a10 we can make the coefficients of X3,X5and X7vanish byandBy setting s5=−arctan(a7/a6),s6=−a3/a1and s7=a5/a6,respectively.Scaling X if necessary,we can assume that a6=1.So,X is reduced to the case(ii).
If a60,a4=0 and a1=0 we can make the coefficients of X3,X5and X7vanish byandBy setting s5=−arctan(a7/a6),s6=−a3/a1and s7=a5/a6,respectively.Scaling X if necessary,we can assume that a6=1.So,X is reduced to the case(iii).
If a6=0,a10 and a40 we can make the coefficients of X2and X5vanish byBy setting s2=a5/a1and s7= −a2/a4ζ,respectively.Scaling X if necessary,we can assume that a1=1.So,X is reduced to the case(iv).
If a6=0,a10,a4=0 and a20 we can make the coefficients of X3and X5vanish byBy setting s2=a5/a1and s7=−a3/a2,respectively.Scaling X if necessary,we can assume that a1=1.So,X is reduced to the case(v).
If a6=0,a10,a4=0 and a2=0 we can make the coefficient of X5vanish by.By setting s2=a5/a1.Scaling X if necessary,we can assume that a1=1.So,X is reduced to the case(vi).
If a6=0,a1=0 and a40 then we can make the coefficients of X2and X7vanish byBy setting s2=a7/a4ζ and s7= −a2/a4ζ,respectively.Scaling X if necessary,we can assume that a4=1.So,X is reduced to the case(vii).
If a6=0,a1=0,a4=0 and a20 then we can make the coefficients of X3,X5and X7vanish by Fs11,By setting s1=−a5/a2,s3=a7/a2and s7=−a3/a2,respectively.Scaling X if necessary,we can assume that a4=1.So,X is reduced to the case(viii).
If a6=0,a1=0,a4=0,a2=0 and a70 then we can make the coefficients of X5vanish byBy setting s6=−a5/a7.Scaling X if necessary,we can assume that a7=1.So,X is reduced to the case(ix).
If a6=0,a1=0,a4=0,a2=0,and a7=0 then X is reduced to the case(x). ?
Taking into account the fact that each one-parameter group Gigenerated by the resulted one-dimensional subalgebras,...,is a symmetry group and generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,exponentiation shows that:
Corollary 3 If H=h(x,y,t)is a solution of the(2D)MKS equation(4),so are the following functions

where ε is any real number.
3.2 Optimal System of Two-Dimensional Symmetry Subalgebras of the(2D)MKS Equation
Constructing the two-dimensional optimal system,i.e.,classification of two-dimensional subalgebras of g,is the next process.This step is performed by selecting one of the vector fields as stated in theorem(4).So get an optional vector Y=b1X1+b2X2+ ···b7X7and a vector X of one-dimensional subalgebras.So we must have
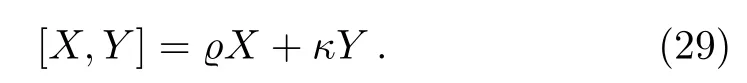
Equation(29)leads us to the system
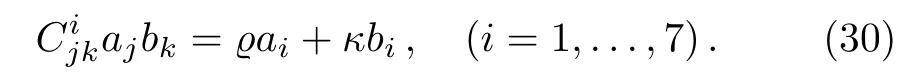
The solutions of the system(30),give one of the two-dimensional generator and the second generator is X1or,Xi,i=2,3,4,5,6,7 if selected.After the construction of all two-dimensional subalgebras,for every vector fields of theorem 4,they need to be simplified by the action of adjoint matrices in the manner analogous to the way of one-dimensional optimal system.Suppose h=Span{X,Y}is a two-dimensional subalgebra of g.Accordingly we have:Case 1 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]=ϱX+κY.Now four states may be happened:
(i)If a2,a30 then we have:
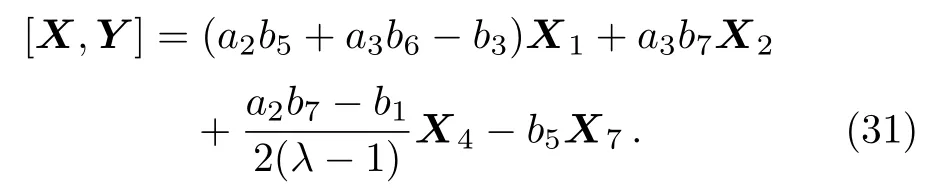
Equation(31)leads us to the system:
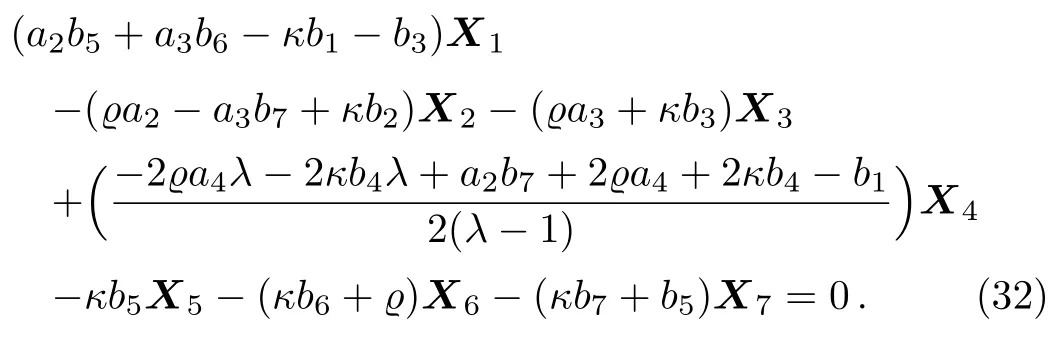
By solving the system(32)and a suitable change of the base of g,it is deduced that in this case not any two-dimensional subalgebra is constructed.
(ii)If a2=0,a30 then we have:
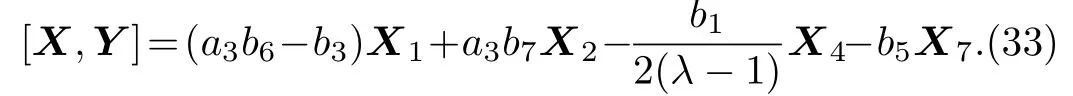
Equation(33)leads us to the system:
By solving the system(34)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
(iii)If a20,a3=0 then we have:

Equation(36)leads us to the system:
By solving the system(37)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(iv)If a2=0,a3=0 then we have:
Equation(39)leads us to the system:
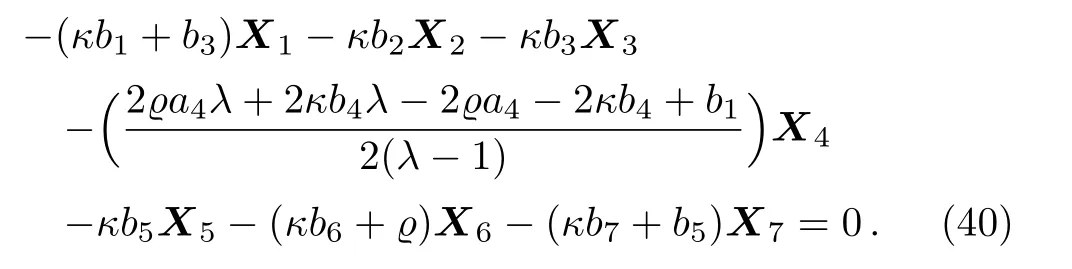
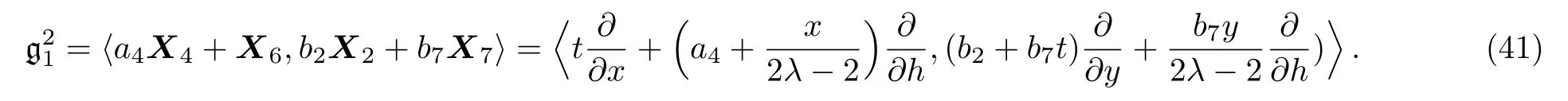
By solving the system(40)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 2 Let X be as the case of,andThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now two states may be happened:
(i)If a20 then we have:
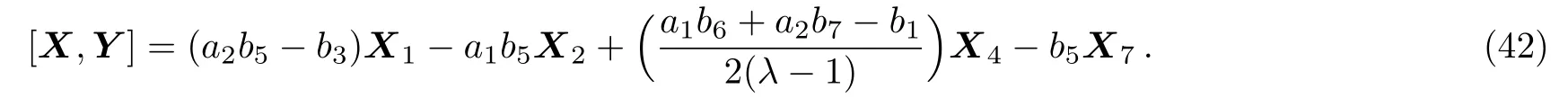
Equation(42)leads us to the system:

By solving the system(43)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(ii)If a2=0 then we have:
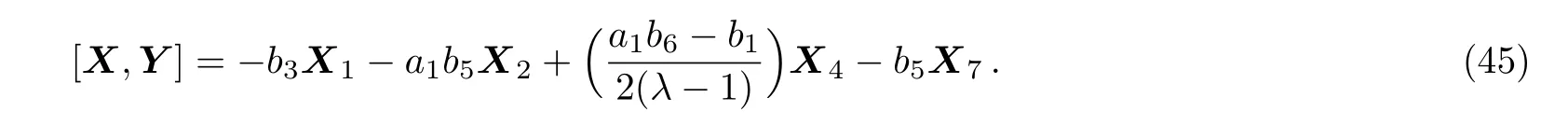
Equation(45)leads us to the system:

By solving the system(46)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
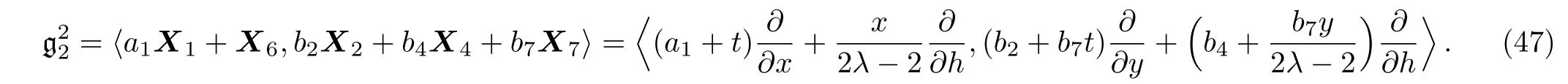
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 3 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now four states may be happened:
(i)If a20,a30 then we have:
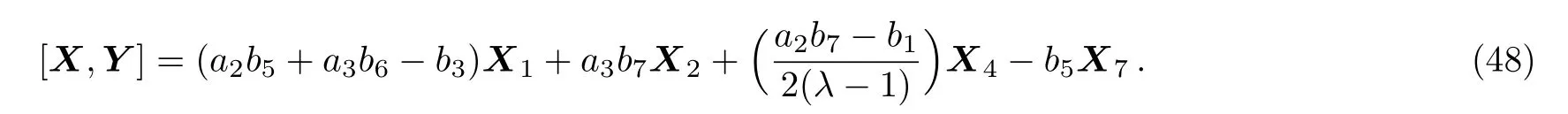
Equation(48)leads us to the system:
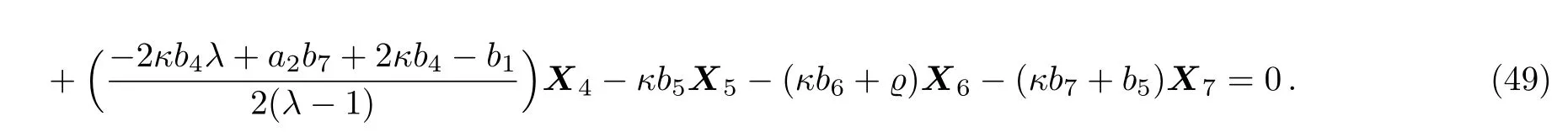
By solving the system(49)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
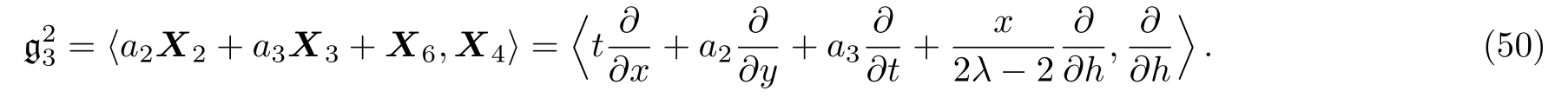
(ii)If a2=0,a30 then we have:
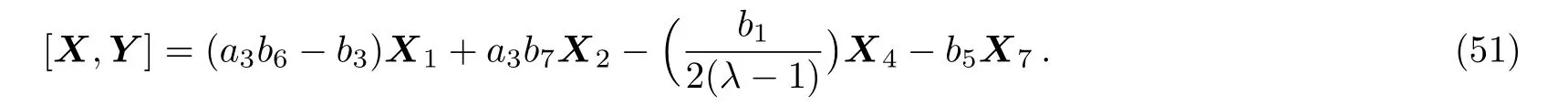
Equation(51)leads us to the system:
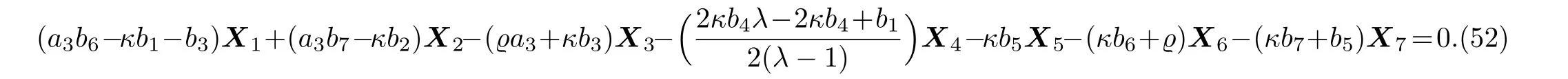
By solving the system(52)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(iii)If a20,a3=0 then we have:
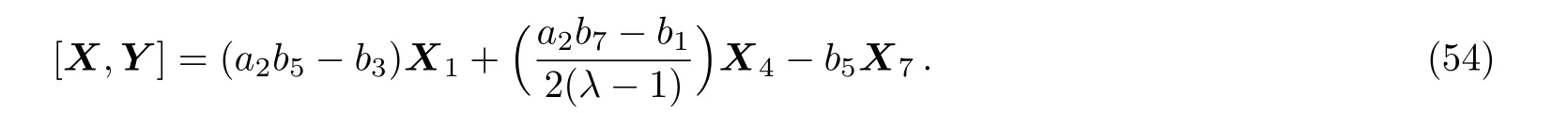
Equation(54)leads us to the system:
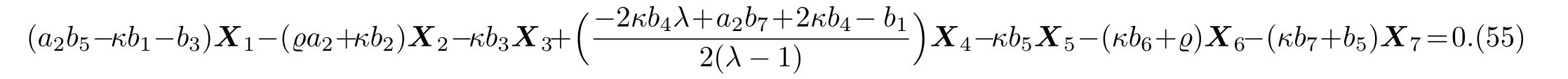
By solving the system(55)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(iv)If a2=0,a3=0 then we have:
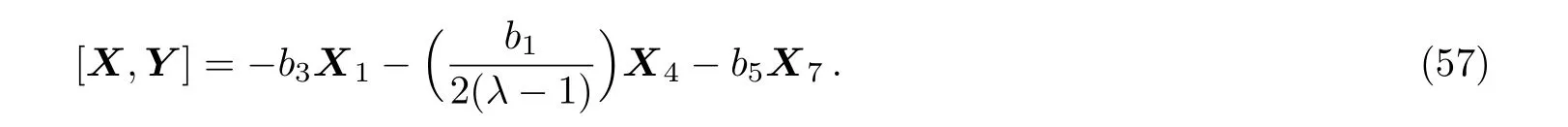
Equation(57)leads us to the system:
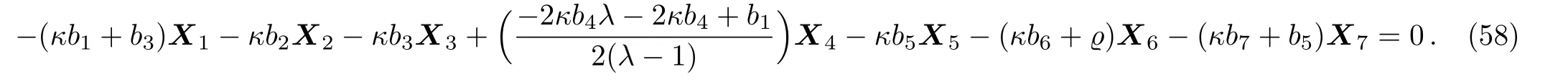
By solving the system(58)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
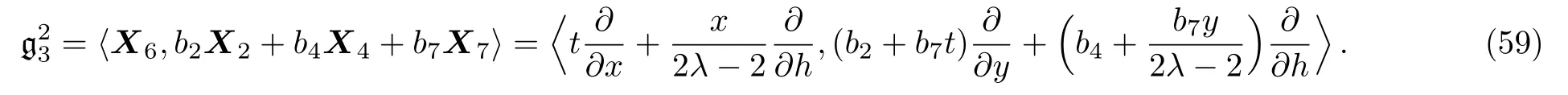
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 4 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now four states may be happened:(i)If a30,a70 then we have:
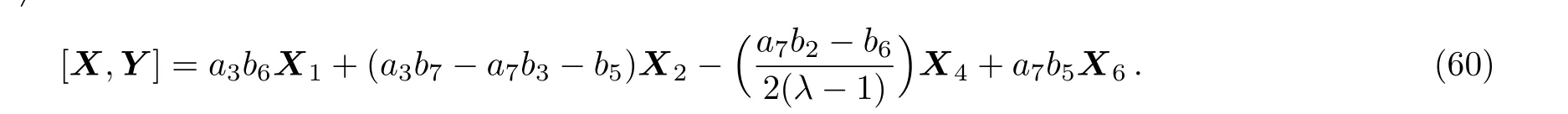
Equation(60)leads us to the system:
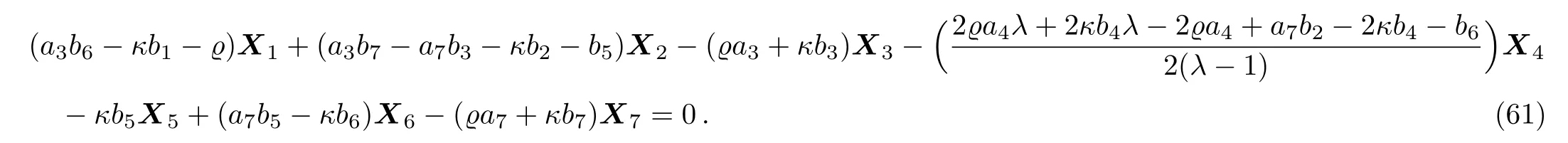
By solving the system(61)and a suitable change of the base of g,it is deduced that in this case not any two-dimensional subalgebra is constructed.
(ii)If a3=0,a70 then we have:
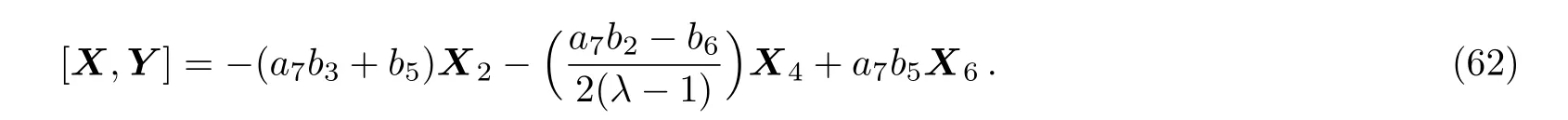
Equation(62)leads us to the system:
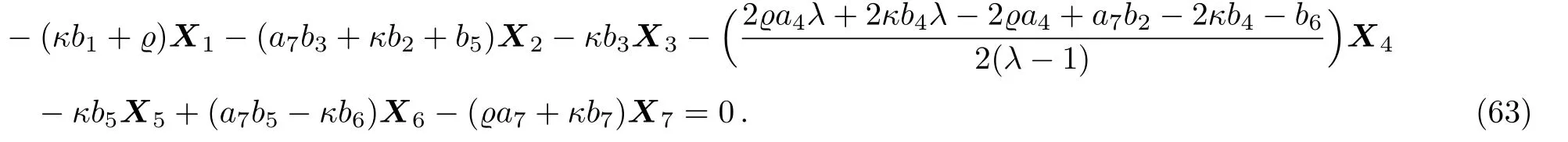
By solving the system(63)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
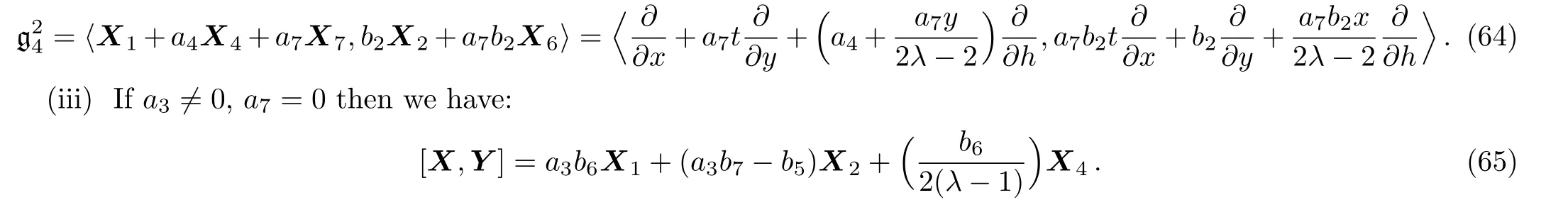
Equation(65)leads us to the system:
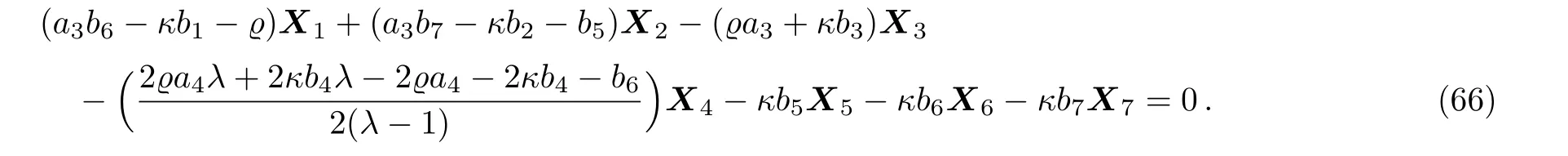
By solving the system(66)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
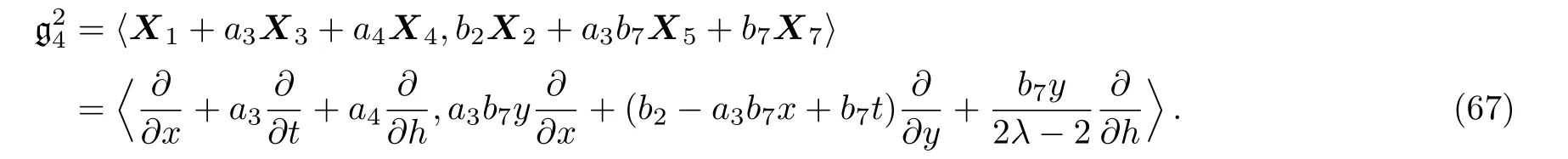
(vi)If a3=0,a7=0 then we have:
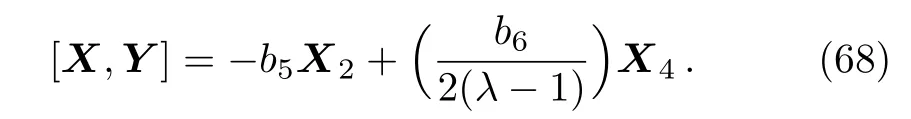
Equation(68)leads us to the system:
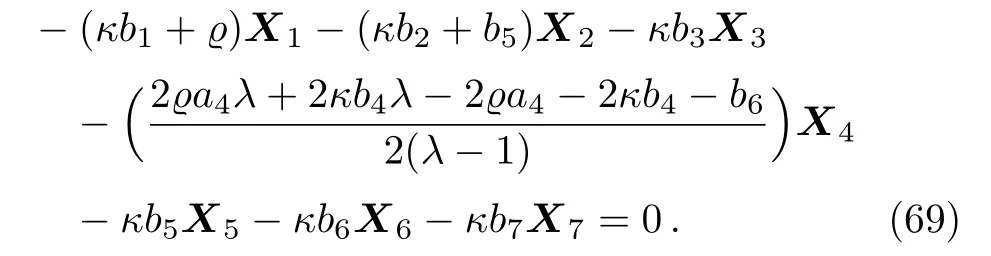
By solving the system(69)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
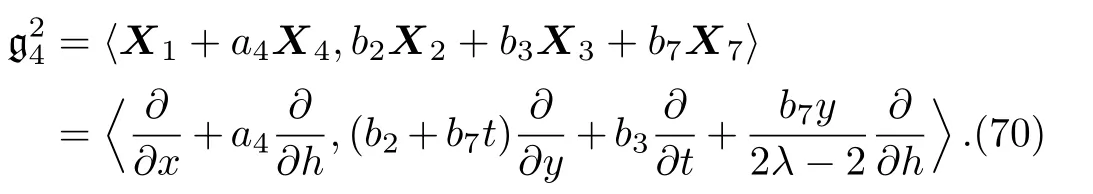
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 5 Let X be as the case of,andThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+κY.Now four states may be happened:
(i)If a70 then we have:
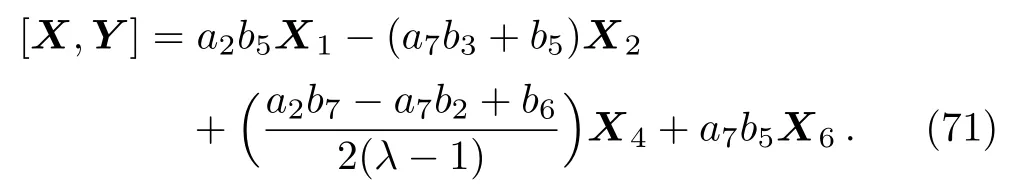
Equation(71)leads us to the system:

By solving the system(72)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
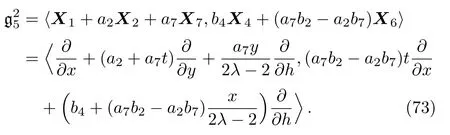
(ii)If a7=0 then we have:
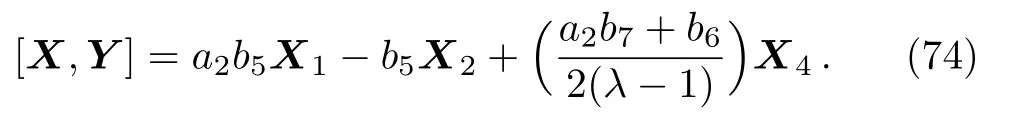
Equation(74)leads us to the system:
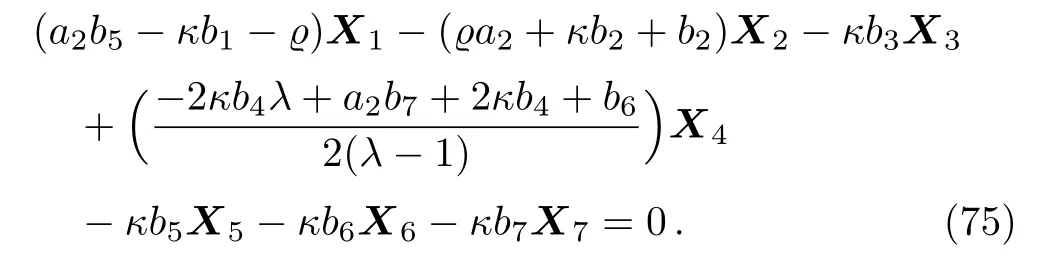
By solving the system(75)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 6 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+κY.Now four states may be happened:
(i)If a30,a70 then we have:

Equation(77)leads us to the system:
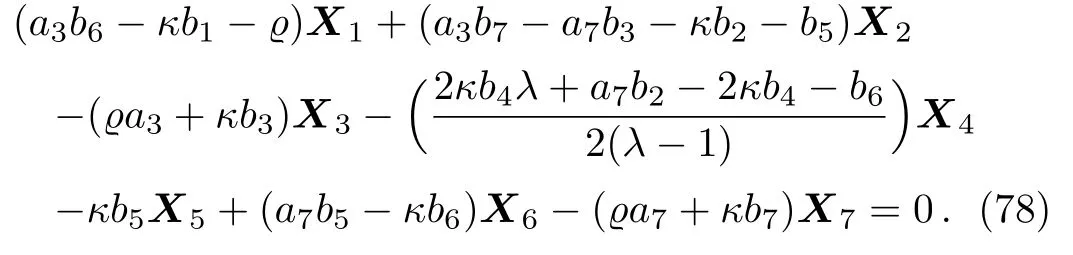
By solving the system(78)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
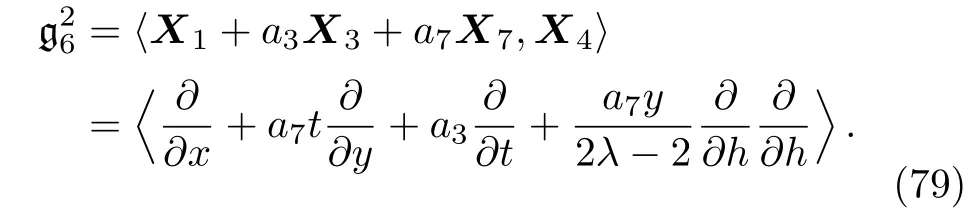
(ii)If a3=0,a70 then we have:
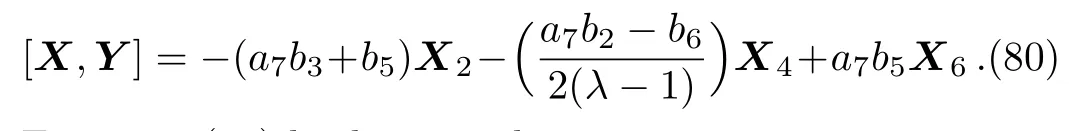
Equation(80)leads us to the system:
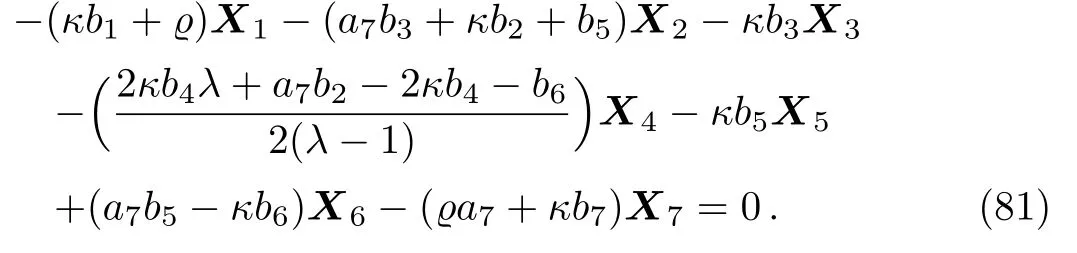
By solving the system(81)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
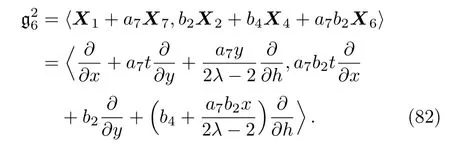
(iii)If a30,a7=0 then we have:
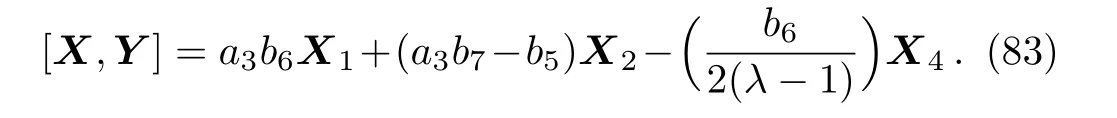
Equation(83)leads us to the system:
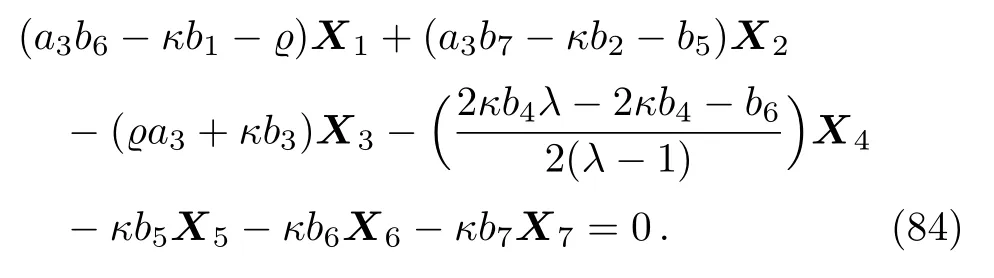
By solving the system(84)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
(iv)If a3=0,a7=0 then we have:
Equation(86)leads us to the system:
By solving the system(87)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 7 Let X be as the case ofThen because h must be closed under the Lie bracket,we
set[X,Y]= ϱX+ κY.Now four states may be happened:
(i)If a30,a50 then we have:
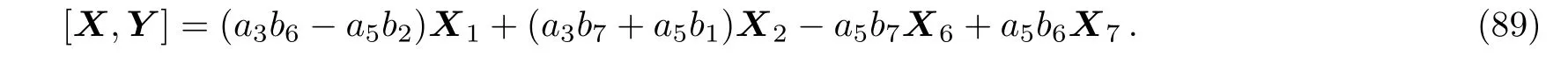
Equation(89)leads us to the system:
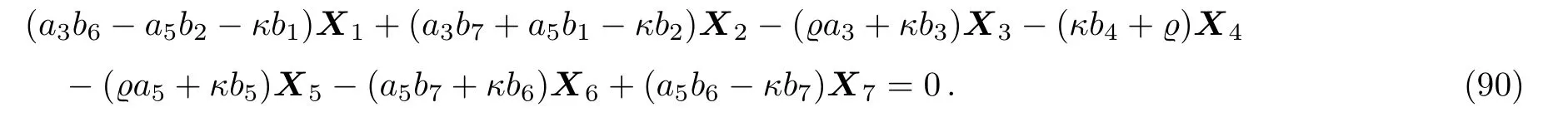
By solving the system(90)and a suitable change of the base of g,it is deduced that in this case not any two-dimensional subalgebra is constructed.
(ii)If a3=0,a50 then we have:
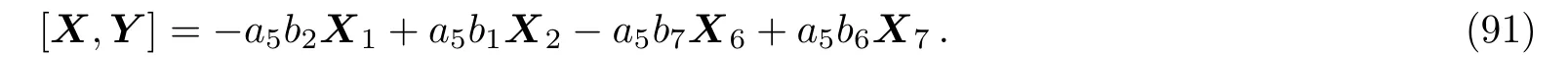
Equation(91)leads us to the system:
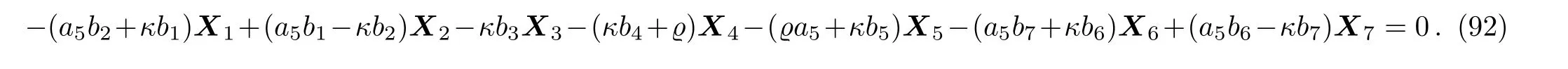
By solving the system(92)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(iii)If a30,a5=0 then we have:

Equation(94)leads us to the system:
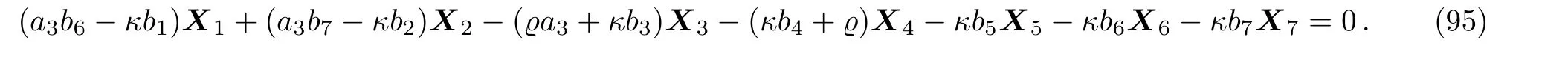
By solving the system(95)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

(iv)If a3=0,a5=0 then we have:

Equation(97)leads us to the system:
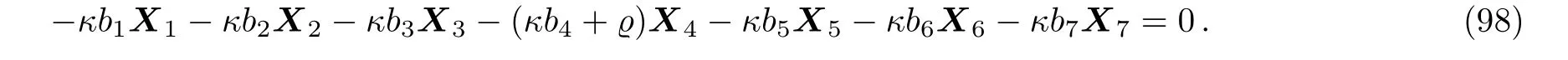
By solving the system(98)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
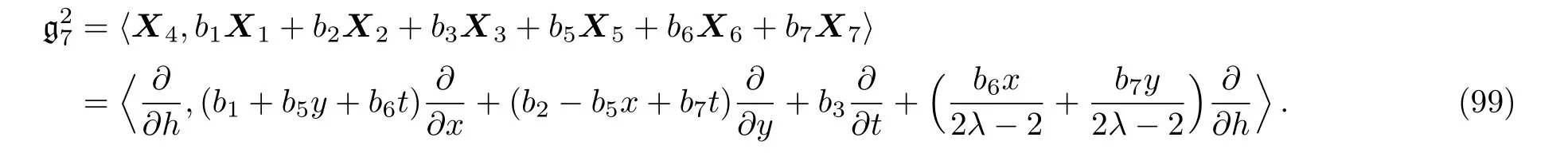
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 8 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now we have:

Equation(100)leads us to the system:

By solving the system(101)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
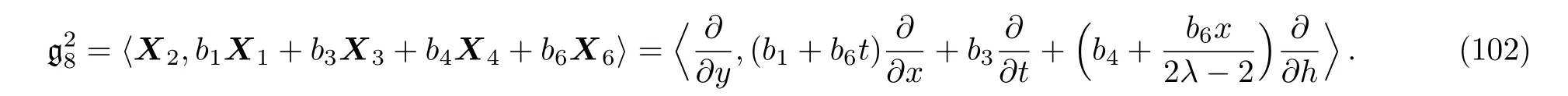
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 9 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now two states may be happened:
(i)If a30 then we have:
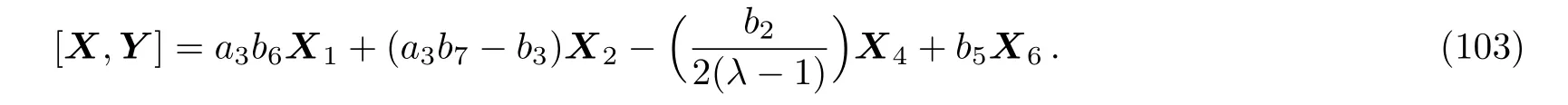
Equation(103)leads us to the system:
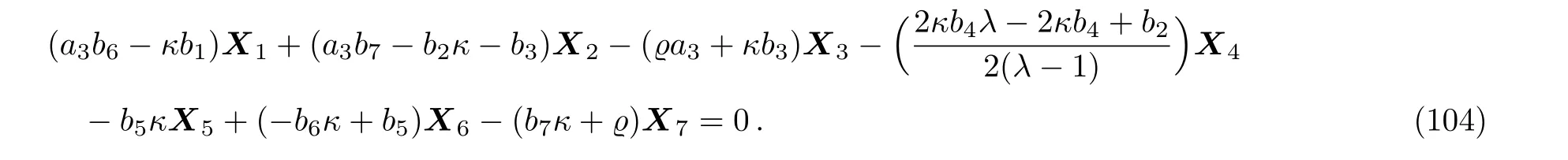
By solving the system(104)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
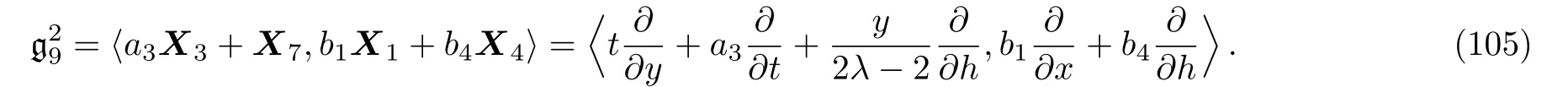
(ii)If a3=0 then we have:
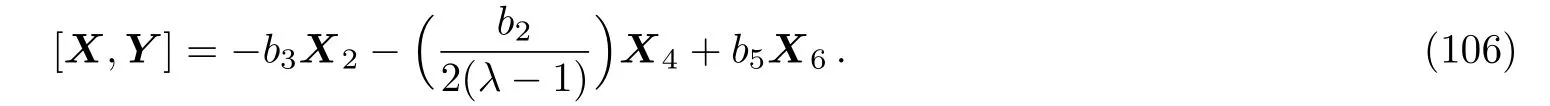
Equation(106)leads us to the system:
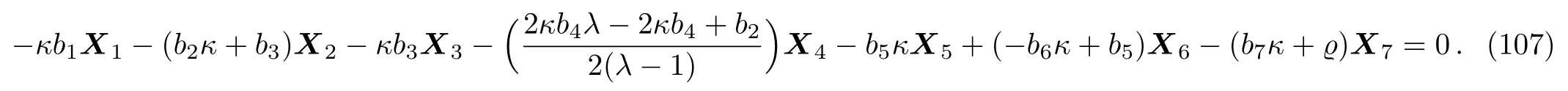
By solving the system(107)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
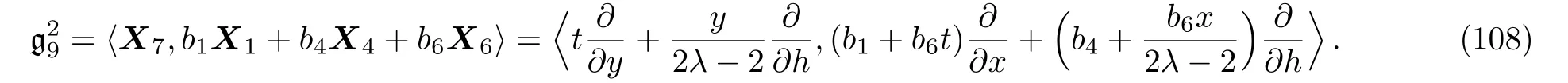
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
Case 10 Let X be as the case ofThen because h must be closed under the Lie bracket,we set[X,Y]= ϱX+ κY.Now three states may be happened:
(i)If a30,a50 then we have:
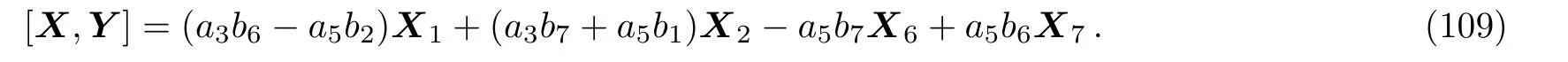
Equation(109)leads us to the system:
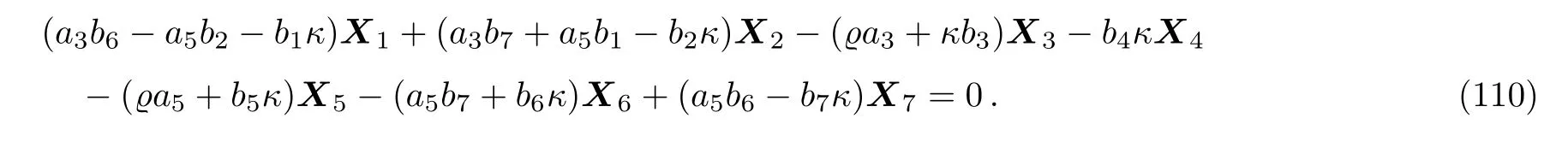
By solving the system(110)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:

Equation(112)leads us to the system:
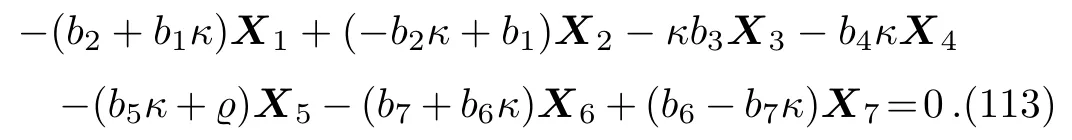
By solving the system(113)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
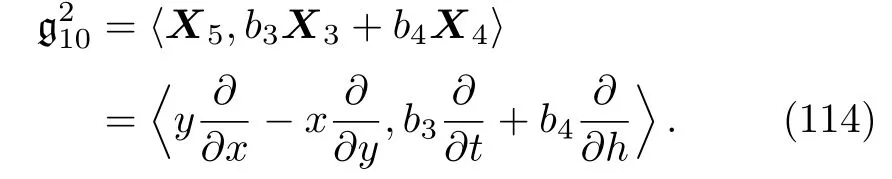
(iii)If a30,a5=0 then we have:
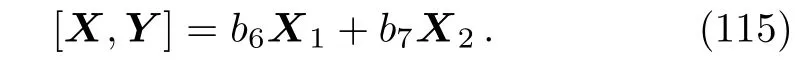
Equation(115)leads us to the system:
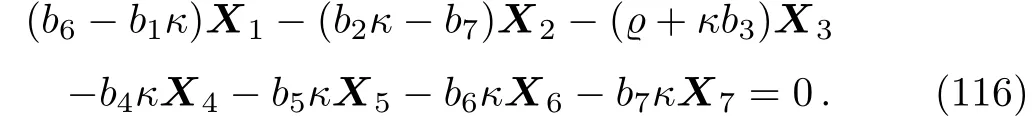
By solving the system(116)and a suitable change of the base of g,the following two-dimensional subalgebra is resulted:
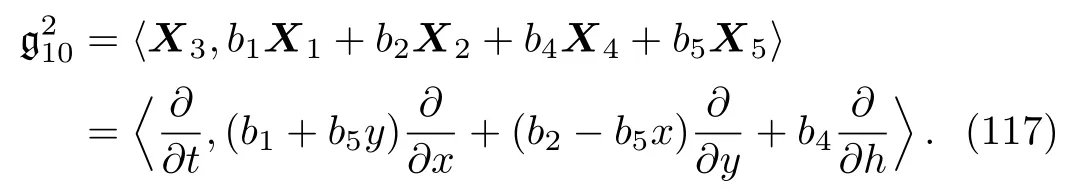
It is worth mentioning that no further simplification of these resulted subalgebras is possible via the transformations
3.3 Optimal System of Three-dimensional Symmetry Subalgebras of the(2D)MKS Equation
This system can be developed by the method of expansion of two-dimensional optimal system. For this purpose,select an arbitrary two-dimensional subalgebra,which is determined in Subsec.3.2,let us consider the first two vector fields mentioned in the previous section and call them W1and W2,thus,we have a subalgebra with basis{W1,W2}, find a vector field W=c1X1+···+c7X7,where ci’s are smooth functions of(x,y,t,h),such the triple{W1,W2,W}generates a basis of a three dimensional algebra.For that it is necessary and sufficient that the vector field Wsatis fies the equations
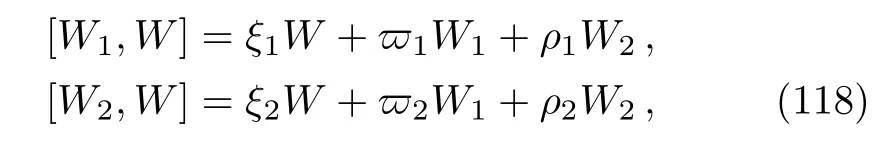
and following from Eq.(118),we obtain the system
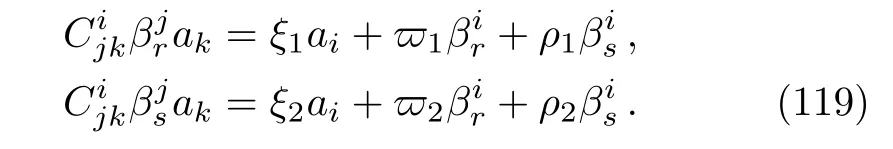
The solutions of system(119)are linearly independent of{W1,W2}and give a three-dimensional subalgebra.This process is applied for the other two couple vector fields illustrated in Subsec.3.2.
Assume that=SpanR{W1,W2,W}be a three dimensional subalgebra of the Lie algebra g,by performing the procedure mentioned above for all of the two couple vector fields,which are resulted in the previous section.It is inferred that in all cases except for the case 6(part(i)),we have:W= β1W1+ β2W2.By a suitable change of the base ofwe can assume that W=0,so that˜g is not a three-dimensional subalgebra.Thus we infer that:Corollary 4 In all cases investigated in Subsec.3.2 except the case 6(part(i)),the symmetry Lie algebra of the(2D)MKS equation has no three-dimensional Lie subalgebra.
In case 6(part(i))of Subsec.3.2 we insert:W1=X1+a3X3+a7X7,W2=X4.Thus due to Eq.(118)we have:
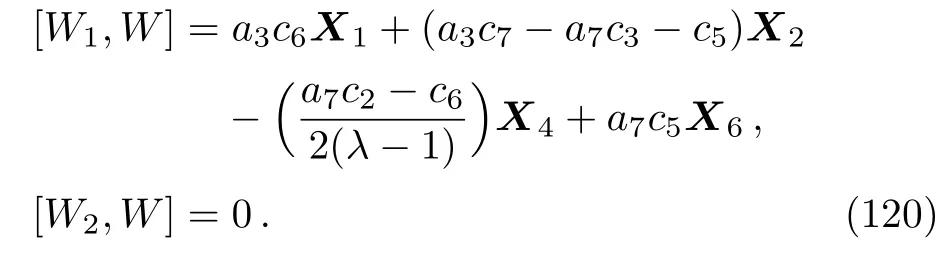
Equation(120)leads us to the following system:
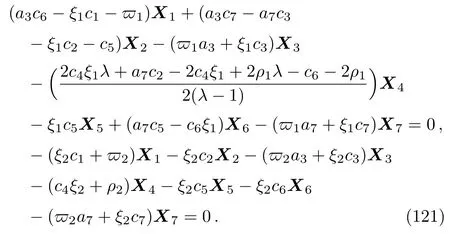
By solving the system(121)and a suitable change of the base of g,the following three-dimensional subalgebra is resulted:
Corollary 5 The symmetry Lie algebra of the(2D)MKS equation(4)has only one three-dimensional Lie subalgebra,which is locally spanned by:
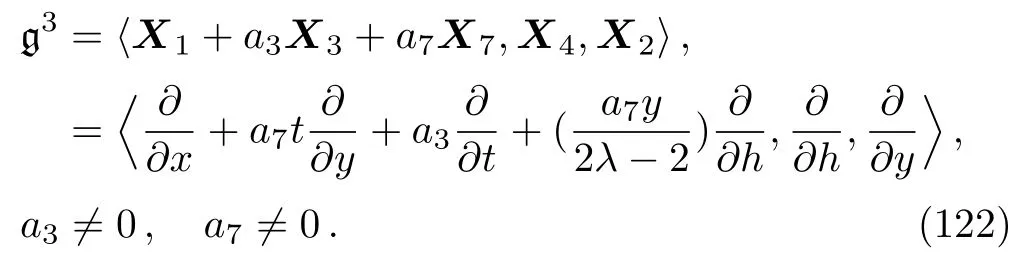
The commutator table of the only resulted three dimensional subalgebra of the(2D)MKS equation i.e.g3is given in Table 3,where the entry in the i-th row and j-th column is defined as[Wi,Wj]=WiWj−WjWi,i,j=1,2,3.
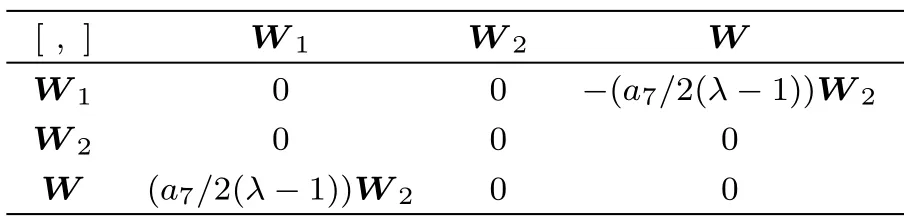
Table 3 Commutator table of g3.
Now in the following we briefly discuss the algebraic structure of the only three-dimensional Lie subalgebra of the(2D)MKS equation:g3has no non-trivial Levi decomposition in the form g3=rטg,because g3has not any non-trivial radical,i.e.if r be the radical of g3,then g3=r.
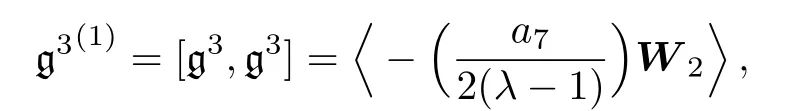
The Lie algebra g3is solvable and non-semisimple.It is solvable,because we have:so the following chain of ideals is deduced:g3(1)⊃{0}.Also,g is not semisimple,because its killing form
is degenerate.
3.4 Optimal System of Four-Dimensional Symmetry Subalgebras of the(2D)MKS Equation
This system can be developed by the method of expansion of three-dimensional optimal system.For this take the only three-dimensional subalgebra of(4),let us consider the three vector fields of g3,and call them Y1,Y2and Y3,thus we have a subalgebra with basis{Y1,Y2,Y3},find a vector field Y=d1X1+ ···+d7X7,where di’s are smooth functions of(x,y,t,h),such the quadruple{Y1,Y2,Y3,Y}generates a basis of a four-dimensional algebra.For that it is necessary a sufficient that the vector field Y satisfies the equations

and following from Eq.(123),we obtain the system
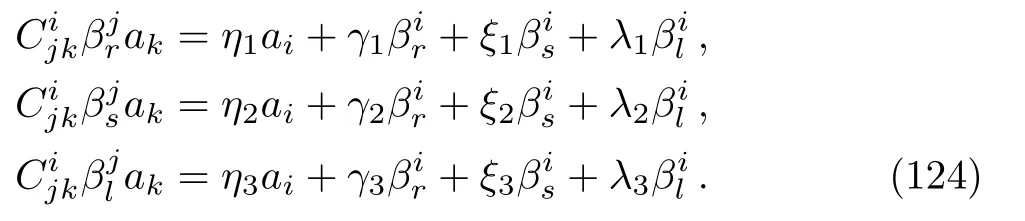
The solutions of system(124)is linearly independent of{Y1,Y2,Y3}and gives a four-dimensional subalgebra.
Assume that˜g=SpanR{Y1,Y2,Y3,Y}be a fourdimensional subalgebra of the Lie algebra g,by performing the procedure mentioned above for the three vector fields of g3,we conclude that Y= β1Y1+β2Y2+β3Y3.By a suitable change of the base of˜g,we can assume that Y=0,so that˜g is not a four-dimensional subalgebra.Thus we infer that:
Corollary 6 The symmetry Lie algebra of the(2D)MKS equation(4)has no four-dimensional Lie subalgebra.
4 Invariant Solutions and Similarity Reduction of the(2D)MKS Equation
An invariant solution of a given PDE system results from invariants of a local symmetry of the PDE,which satisfy an augmented PDE system.This auxiliary PDE system essentially plays the role of a constraint,which is denoted by the invariant surface condition.Thus the obtained invariant solution satisfies both the invariant surface condition and the given PDE system.
It follows that u= Υ(x),with components uν=Υν(x),ν =1,...,m,is an invariant solution of the PDE system E{x;u}resulting from the point symmetry(8),if and only if u=Υ(x)satisfies the following two main conditions:[18]
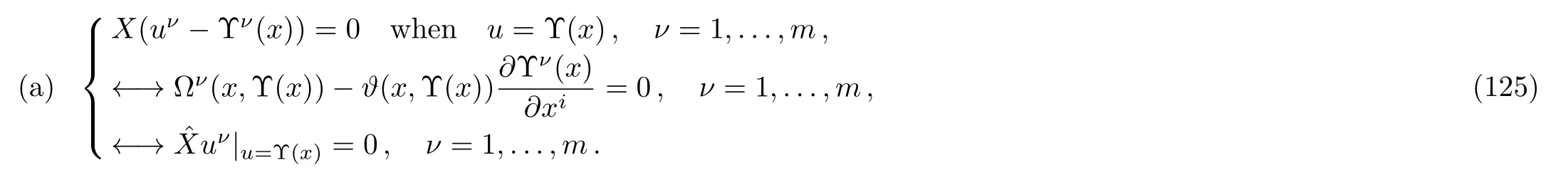
Condition(a)implies that uν= Υν(x)is an invariant surface of the point symmetry(8)for each ν =1,...,m.
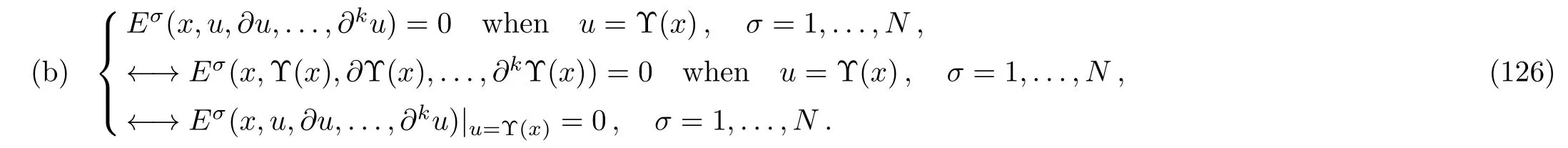
In Eq.(126), ∂jΥ(x)denotes the components ∂jΥµ(x)/(∂xi1...∂xij), µ =1,...,m,for ij=1,...,n with j=1,...,k.Moreover,condition(b)implies that u=Υ(x)is a solution of E{x;u}(5).Having found a point symmetry with infinitesimal generator X given by Eq.(8)through solving the linear system of determining equations(13),one can proceed in the following way in order to solve the systems of Eqs.(125)and(126)to obtain an invariant solution u=Υ(x).

If z1(x,u),...zn−1(x,u),h1(x,u),...,hm(x,u)are n+m−1functionally independent constants of integration,which are resulted from solving the characteristic system of ODEs(127)with the Jacobian∂(h1,...,hm)/∂(u1,...,um)0,then the general solution u=Υ(x)of the invariant surface condition equations(125)is given implicitly by the invariant form

where Hνis an arbitrary differentiable function of its arguments,ν = 1,...,m. Note that z1(x,u),...zn−1(x,u),h1(x,u),...,hm(x,u)are n+m − 1 functionally independent invariants of the one-parameter Lie group of point transformations with the infinitesimal generator X given by Eq.(8),and consequently are n+m−1 canonical coordinates for the one-parameter Lie group of point transformations with the infinitesimal generator X defined by(8)(refer to Ref.[18]for more details).
The(2D)MKS equation(4)is expressed in the coordinates(x,y,t,h),so we ought to search for this equation’s form in specific coordinates in order to reduce it.Those coordinates will be constructed by looking for independent invariants(p,q,r)corresponding to the infinitesimal symmetry generator.Hence,by applying the chain rule,the expression of the equation in the new coordinate leads to the reduced equation.
Having determined the infinitesimals,the similarity solutions of the(2D)MKS equation are listed in Table 4.In the following by applying the resulted invariants,we list the reduced form of the(2D)MKS equation corresponding to infinitesimal symmetries.
(i)For the symmetry operator X1= ∂/∂x the similarity reduced form of the(2D)MKS equation is as follows:
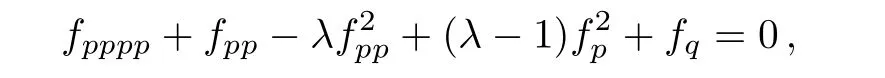
where p=y,q=t,and h=f(p,q).
(ii)For the symmetry operator X2= ∂/∂y the similarity reduced form of the(2D)MKS equation is as follows:
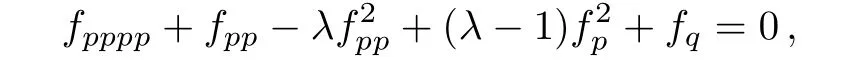
where p=x,q=t and h=f(p,q).
(iii)For the symmetry operator X3= ∂/∂t the similarity reduced form of the(2D)MKS equation is as follows:
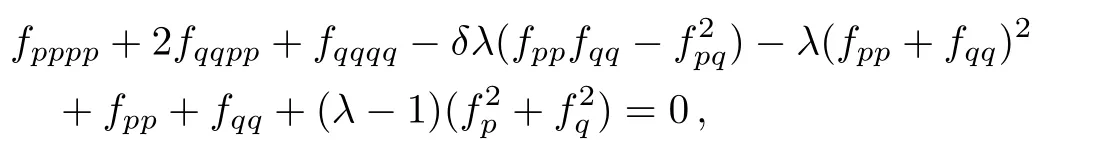
where p=x,q=y,and h=f(p,q).
(iv) For the symmetry operator X5=y(∂/∂x) −x(∂/∂y)the similarity reduced form of the(2D)MKS equation is as follows:

where p=t,q=x2+y2,and h=f(p,q).
(v)For the symmetry operator
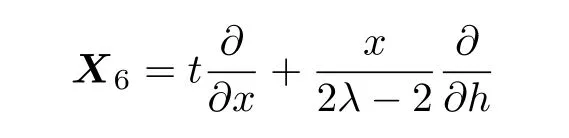
the similarity reduced form of the(2D)MKS equation is as follows:

where p=y,q=t,and f(p,q)+x2/4(λ−1)t.
(vi)For the symmetry operator
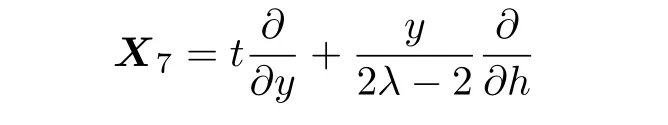
the similarity reduced form of the(2D)MKS equation is as follows:

where p=x,q=t,and h=f(p,q)+y2/4(λ −1)t.
(vii)For the symmetry operator
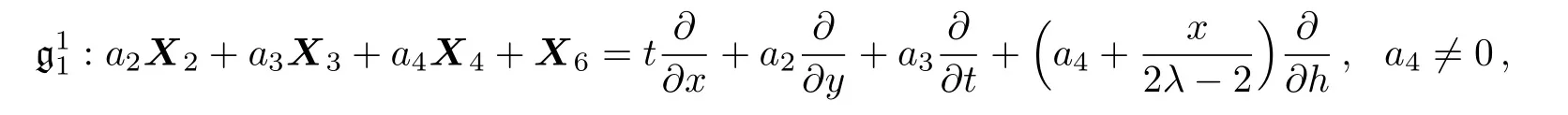
the similarity reduced form of the(2D)MKS equation is as follows:
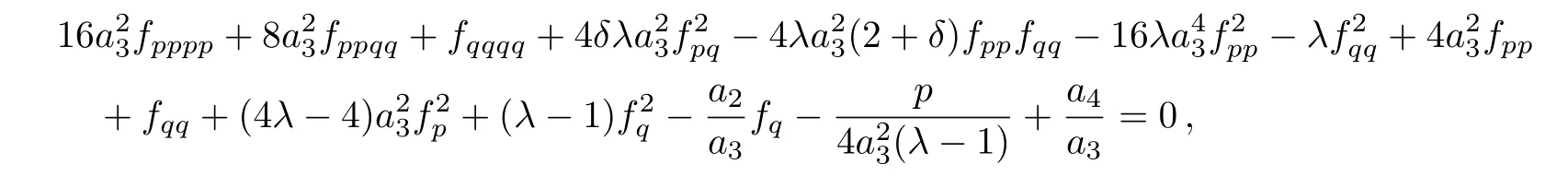
where
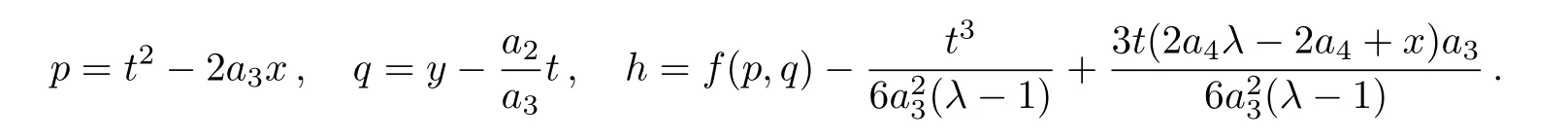
(viii)For the symmetry operator

the similarity reduced form of the(2D)MKS equation is as follows:
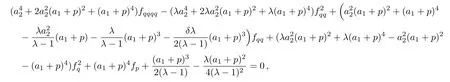
where p=t,
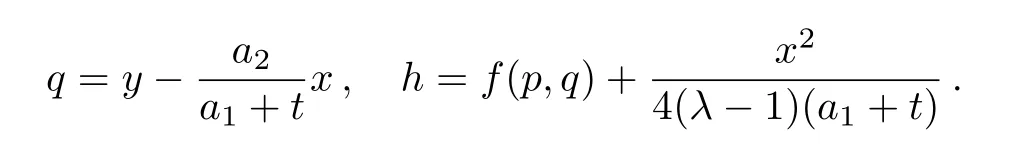
(ix)For the symmetry operator
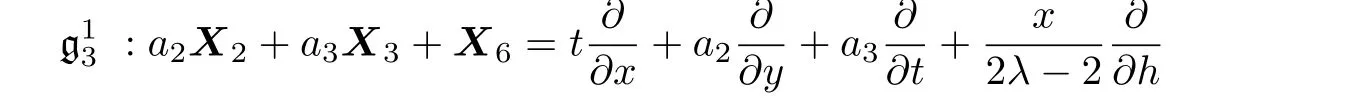
the similarity reduced form of the(2D)MKS equation is as follows:
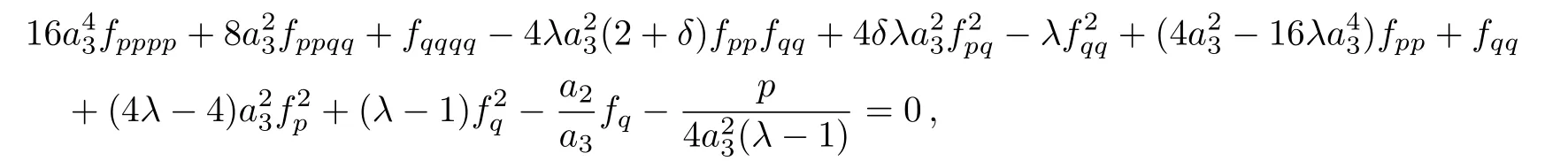
where p=t2−2a3x,q=y−(a2/a3)t and h=f(p,q)+(3ta3x−t3)/6(λ−1).
(x)For the symmetry operator

the similarity reduced form of the(2D)MKS equation is as follows:
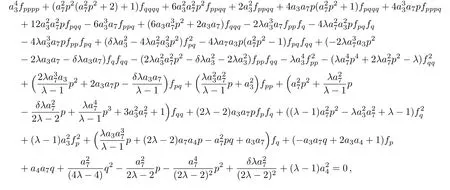
where
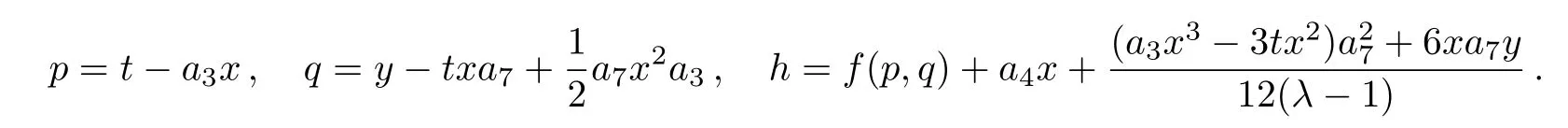
(xi)For the symmetry operator
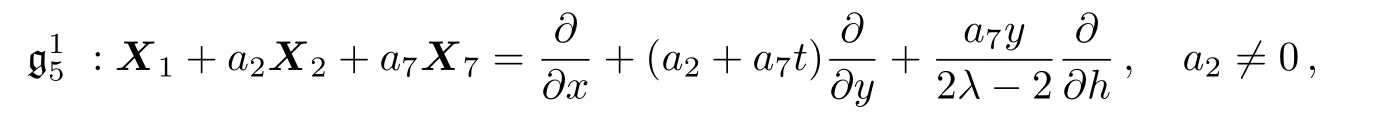
the similarity reduced form of the(2D)MKS equation is as follows:
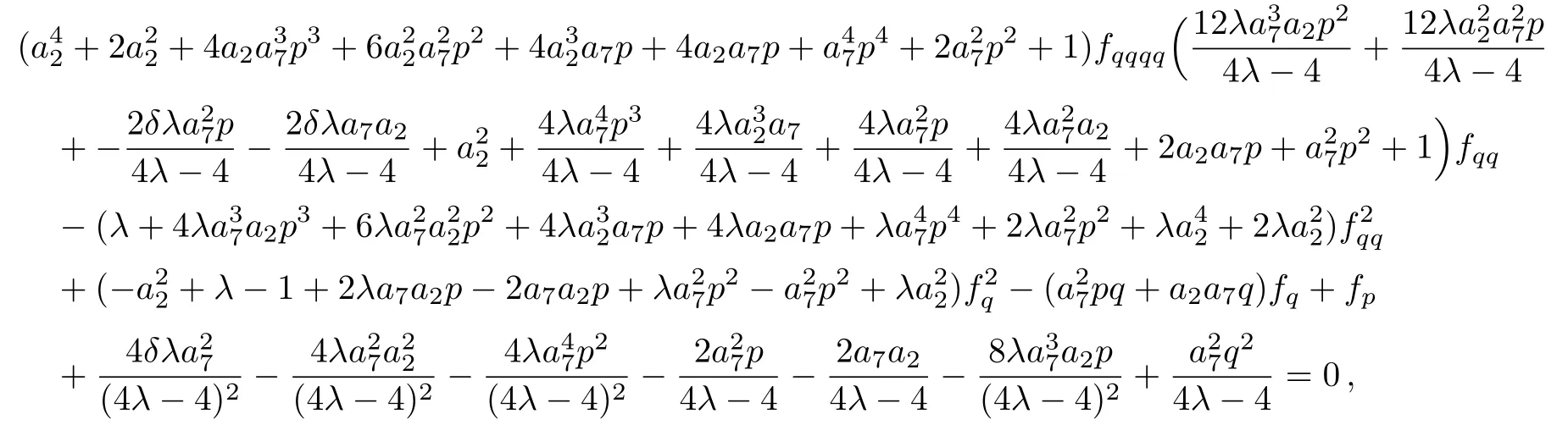
where
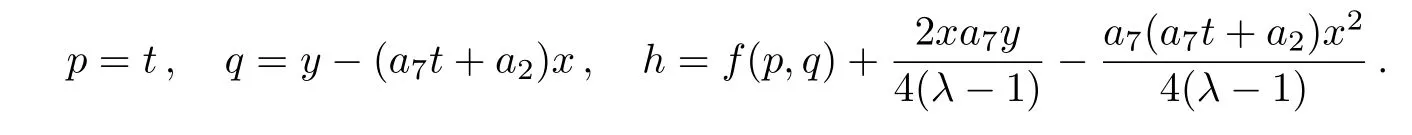
(xii)For the symmetry operator
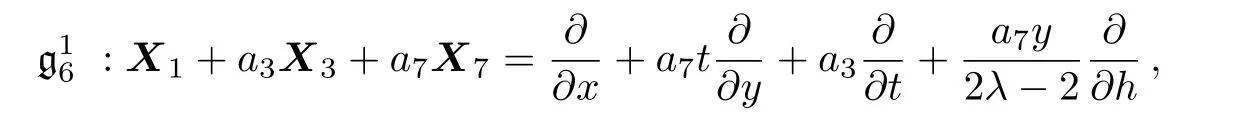
the similarity reduced form of the(2D)MKS equation is as follows:
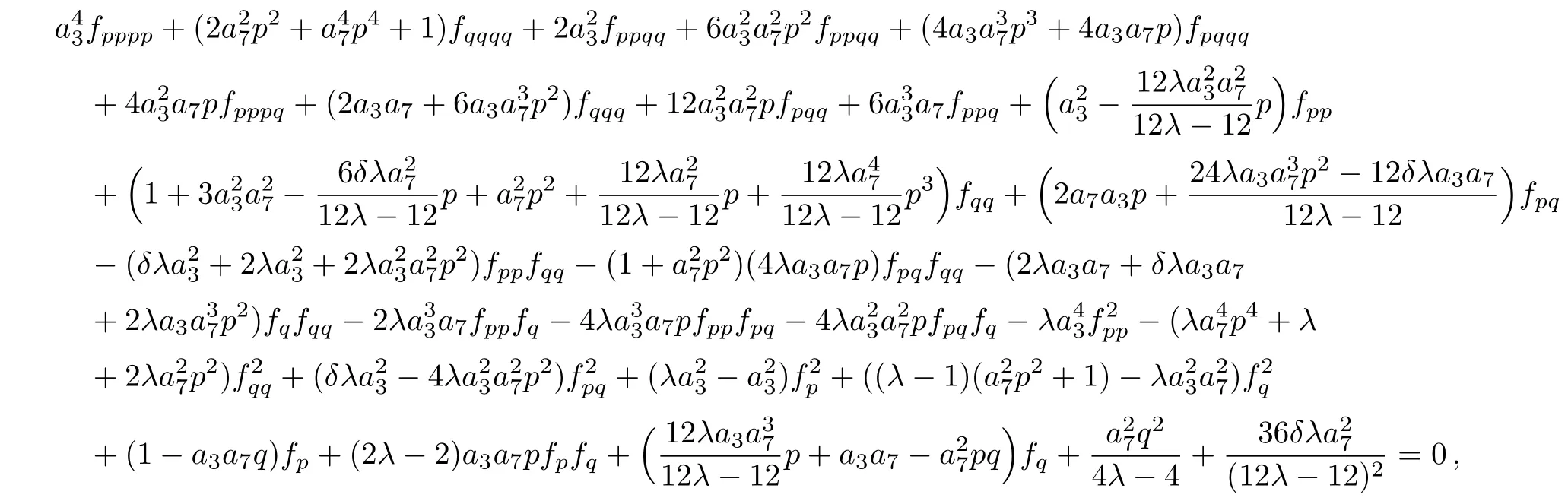
where p=t−a3x,q=y−txa7+(1/2)a7x2a3and
(xiii)For the symmetry operator:a3X3+X4+a5X5=a5y(∂/∂x)− a5x(∂/∂y)+a3(∂/∂)t+ ∂/∂h,the similarity reduced form of the(2D)MKS equation is as follows:
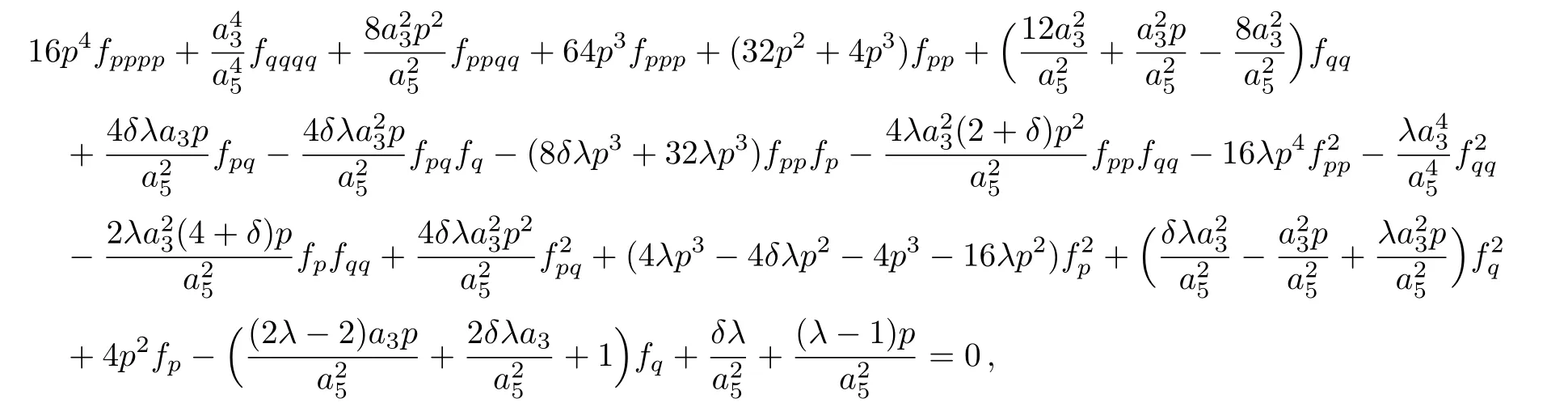
where p=x2+y2,q=t−(a3/a5)arctan(x/y),and h=f(p,q)+[arctan(x/y)]/a5.
(xiv)For the symmetry operator
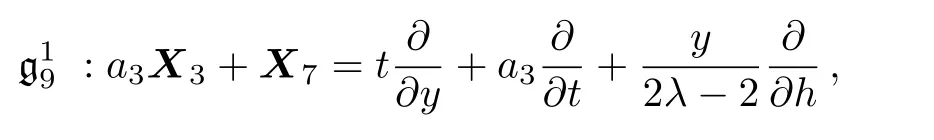
the similarity reduced form of the(2D)MKS equation is as follows:

where p=x,q=t2−2a3y,and h=f(p,q)+(3ta3y−t3)/6(λ−1).
(xv)For the symmetry operator:a3X3+a5X5=a5y(∂/∂x)− a5x(∂/∂y)+a3(∂/∂t),the similarity reduced form of the(2D)MKS equation is as follows:

where p=x2+y2,q=t−(a3/a5)arctan(x/y),and h=f(p,q).

Table 4 Lie Invariants and Similarity Solutions of the(2D)MKS equation.
5 Nonclassical Symmetries of the(2D)MKS Equation
In this section,the so called nonclassical symmetry method is performed for the(2D)MKS equation.Beside the classical symmetries,the nonclassical symmetry method can be applied in order to obtain some other solutions for a system of PDEs and ODEs.The fact that symmetry reductions for many PDEs can not be obtained via the classical symmetry method,was the motivation to create several generalizations of the classical Lie group method for symmetry reductions.The notion of nonclassical symmetries was firstly introduced in 1969 by Bluman and Cole[30]to study the symmetry reductions of the heat equation.The nonclassical symmetry method has become the focus of a lot of research and many applications to physically important partial differential equations.
In the nonclassical method, first of all we search for functions ϑi(x,u),Ωµ(x,u),i=1,...,n,µ =1,...,m,as a consequence(8)is a nonclassical symmetry of the augmented PDE system A{x;u},which includes the given PDE system E{x;u}Eq.(5)together with the invariant surface condition equations
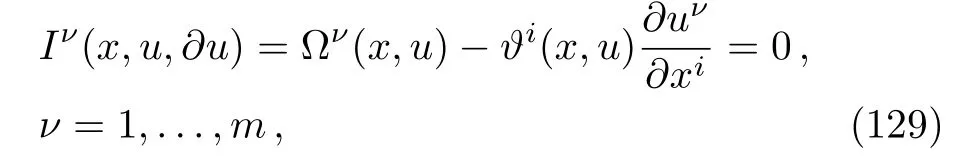
and the differential consequences corresponding to Eq.(129).Hence,an over-determined set of nonlinear determining equations for the unknown functions ϑi(x,u),Ωµ(x,u),i=1,...,n,µ =1,...,m is achieved.Furthermore,it can be clearly demonstrated that for any arbitrary set of ϑi(x,u),Ωµ(x,u),i=1,...,n,µ =1,...,m,Eq.(8)can be regarded as a symmetry of the invariant surface condition equations(129).This means that the nonclassical method comprises Lie us classical method.In addition,because of the substitution of the invariant surface condition equations(129)and their corresponding differential consequences into the symmetry determining equations(13),the resulting set of determining equations is nonlinear.
The invariant surface condition equations(129)can fundamentally be regarded as a collection of constraint equations of a particular form.Specifically,the nonclassical procedure is precisely equivalent to searching for all solutions of the PDE system(5)of the form(129)for any possible set of ϑi(x,u), Ωµ(x,u),i=1,...,n,µ=1,...,m.Therefore,the set of resulting determining equations satisfied by ϑi(x,u),Ωµ(x,u),i=1,...,n,µ=1,...,m,can be considered as the compatibility conditions for the existence of solutions of the auxiliary PDE system A{x;u},which comprises the PDE system E{x;u}and the constraint equations(129).Consequently,a solution of a given PDE system E{x;u}Eq.(5)is a nonclassical solution whenever it is deduced as an invariant solution of the augmented PDE system A{x;u},which is consisting of the PDE system E{x;u}Eq.(5),the constraint equations(129)and their corresponding differential consequences.Thus it is not determined as an invariant solution of the PDE system(5)with respect to its resulted local Lie symmetries.
As mentioned above,for the nonclassical method,it is necessary to add the invariance surface condition to the given equation,and then apply the classical symmetry method.This fact can also be conveniently stated as:
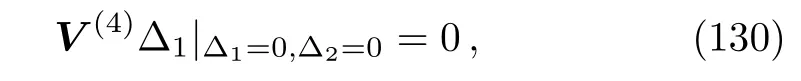
where V is defined as similar as Eq.(8)and∆1and∆2are given by:
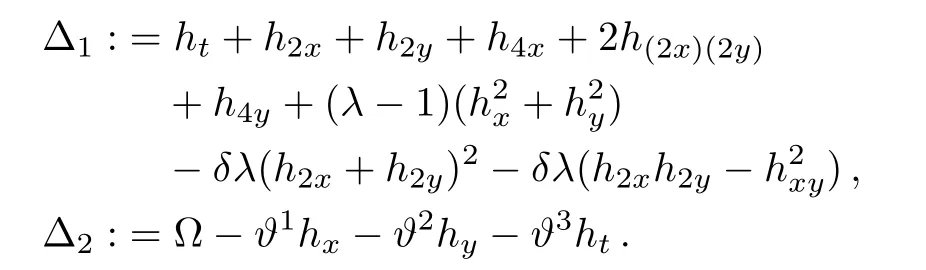
According to Ref.[18],from the structure of the constraint invariant surface condition equation∆2,in applying the nonclassical procedure,without loss of generality,when solving the determining equations,two general simplifying cases could be considered,namely,ϑ3=1;ϑ3=0,ϑ1=1.This follows from the observations that if ϑ30,then the constraint invariant surface condition equation∆2can be divided through by ϑ3,consequently,without loss of generality,one can set ϑ3=1.Similarly,if ϑ3=0, ϑ10,then the constraint invariant surface condition∆2can be divided through by ϑ1,as a consequence,without loss of generality,one can set ϑ1=1.
Now we exhaustively analyze the following two distinct cases:
♣ Case(1):ϑ3=1.
In this case using∆2we have:
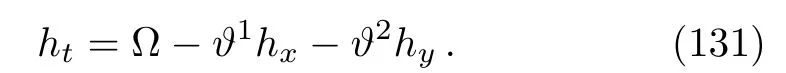
First,total differentiation Dtof Eq.(4)gives

Substituting ϑ1hxtand ϑ2hytto both sides,we can get
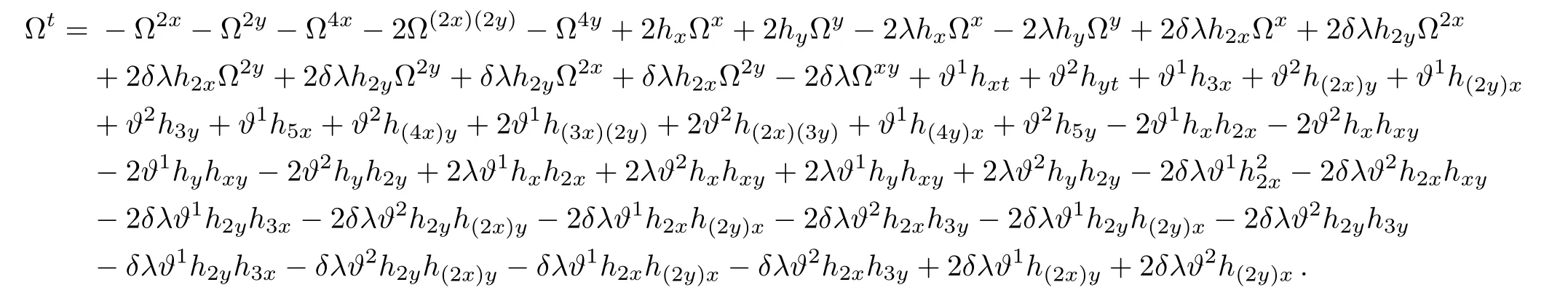
By virtue of
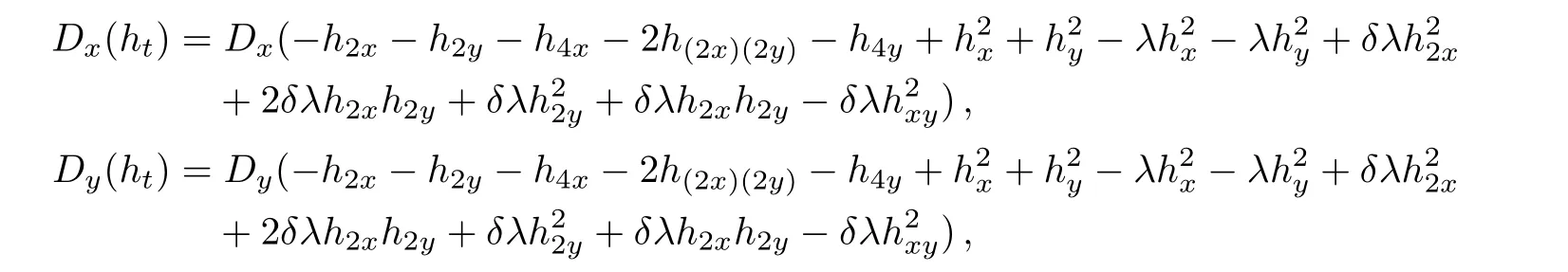
gives
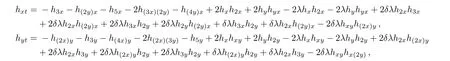
so the governing equation is attained as follows:

where the coefficients Ωt,Ωx,Ωy,Ω2x,Ω2y,Ω4x,Ωxy,Ω(2x)(2y)Ω4yin the governing equation are given by

Substituting them into the governing equation,we can get the determining equations for the symmetries of the(2D)MKS equation.Hence,the determining equations of the nonclassical symmetries of the original equation(4)are obtained by inserting ϑ3=1 into the determining equations.After solving the system resulted by this procedure,the solutions we found were exactly the same as the solutions deduced through the classical symmetry approach.Hence,it is concluded that no additional symmetries of nonclassical type,are specific for our analyzed model.
Corollary 7 In this case,the(2D)MKS equation admits no supplementary symmetries of nonclassical type.
♣ Case(2)ϑ3=0,ϑ1=1.In this case,by considering the corresponding constraint invariant surface condition and its associated differential consequences,it is deduced that:

where ci,i=1,...,4 are arbitrary constants.Consequently,the resulted nonclassical infinitesimal symmetry generators are as follows:

Theorem 5 The Lie group of nonclassical symmetries of the(2D)MKS equation(4)has a six-dimensional Lie subalgebra generated by the following vector fields:
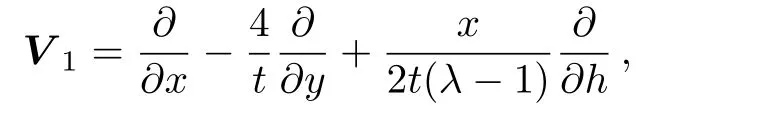

Proof
The commutation relations between the vector fields V1,...,V4is given by Table 5,the entry in row i and column j representing[Vi,Vj]:

Table 5 Commutation table of the resulted nonclassical symmetries.
As we see above in Table 5,the infinitesimal symmetries V1,...,V4do not form a Lie algebra.Since,the Lie bracket of two point symmetry infinitesimal generators is also an infinitesimal symmetry generator,[20−21]we insert
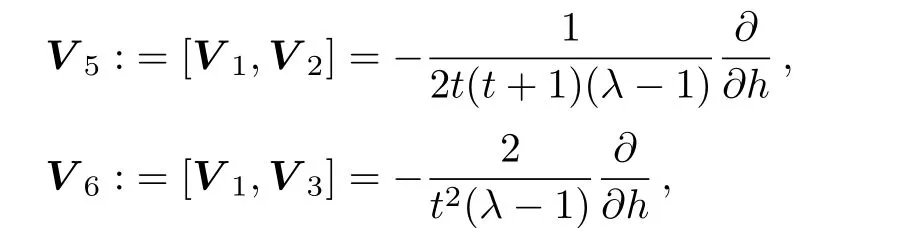
and consider them as the other infinitesimal symmetries.Hence,by adding V5and V6to other four vector fields,a Lie algebra of nonclassical symmetry generators will be constructed.The commutation relations between the vector fields V1,...,V6is given in Table 6.Consequently,we have constructed a Lie algebra of nonclassical infinitesimal symmetries of the(2D)MKS equation,which is spanned by the six vector fields V1,...,V6.So,the proof completes.

Table 6 Commutation table of the(2D)MKS equation’s Lie algebra of nonclassical symmetries˜g.
As a consequence,the general group of nonclassical symmetries can be obtained by considering a general linear combination of the given vector fields. For one-dimensional subalgebras indeed this classification is essentially the same as the classifying the orbits of the adjoint representation.If only one representative is selected from each family of equivalent subalgebras,an optimal set of subalgebras is created.Consequently,a minimal list of invariant solutions from which all the other invariant solutions of one-dimensional subalgebras can be obtained,is constructed via transformations.
Each Vi,i=1,...,6,of the basis symmetries generates an adjoint representation(or interior automorphism)Ad(exp(εVi))defined by the Lie series
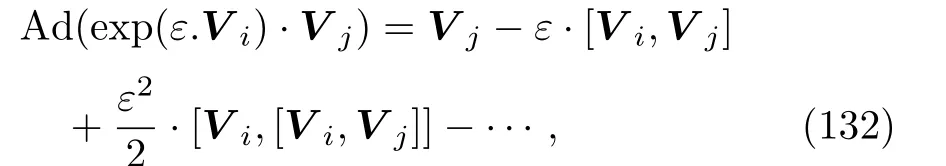
where[Vi,Vj]is the commutator for the Lie algebra,ε is a parameter,and i,j=1,...,6.In Table 7 all the adjoint representations corresponding to the Lie group of nonclassical symmetries of the(2D)MKS equation(4)is presented,with the(i,j)entry indicating Ad(exp(εVi))Vj.
We can expect to simplify a given arbitrary element,

of the(2D)MKS equation’s Lie algebra of nonclassical symmetriesNote that the elements ofcan be represented by vectors α =(α1,...,α6) ∈ R6,since each of them can be written in the form(133)for some constants α1,...,α6.Hence,the adjoint action can be regarded as a group of linear transformations of the vectors(α1,...,α6).

Table 7 Adjoint representation generated by nonclassical symmetries of Eq.(4).
Therefore,we can state the following theorem:
Theorem 6 An optimal system of one-dimensional Lie subalgebras of nonclassical symmetries associated to the(2D)MKS equation(4)is provided by those generated by
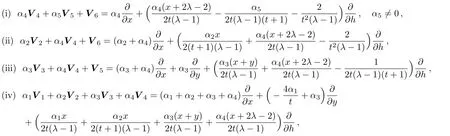
where αi,i=1,...6 are arbitrary real numbers.
Proofdefined by V 7→Ad(exp(εiVi)·V)is a linear map,for i=1,...,6.The matrixwith respect to basis{V1,...,V6}is
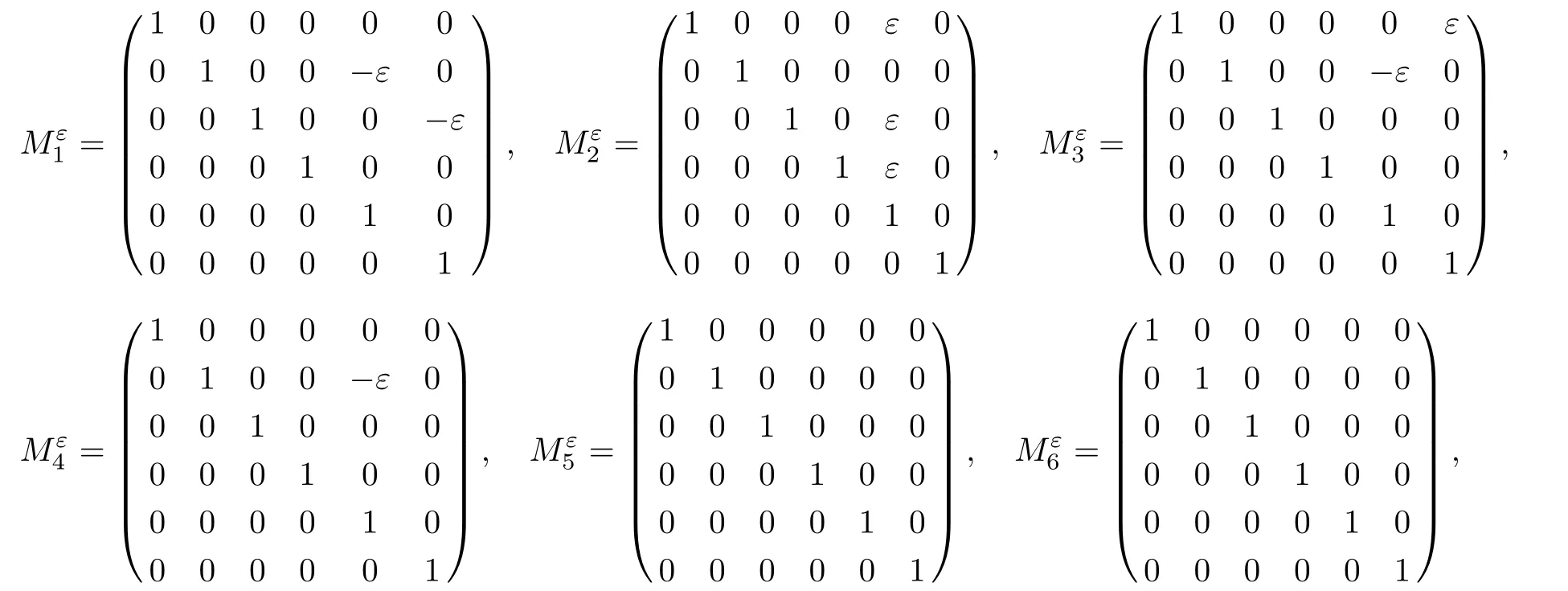
respectively.Letthen it is observed that
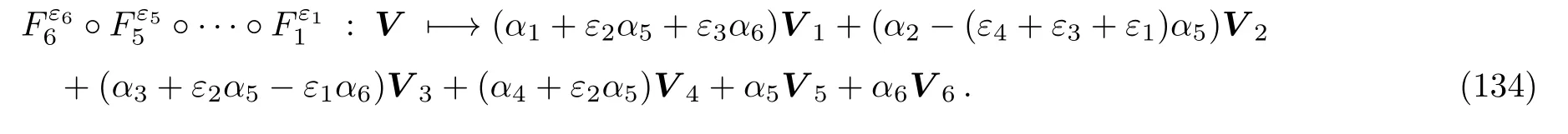
In order to classify the one-dimensional Lie subalgebras of the resulted nonclassical symmetries,the following cases are planned such that in each case,by acting a finite num-
If α6,α50 then we can make the coefficients of V3,V1and V2vanish byBy setting ber of the adjoint representationsby proper selection of parameters εiin each stage,it is gradually tried to make the coefficients of V vanish and to acquire the most simple form of V.
Now,we can simplify V as follows:ε1= α3/α6,ε3= −α1/α6,and ε4= α2/α5,respectively.Scaling V if necessary,we can assume that α6=1.So,V is reduced to the case(i).
If α60,α5=0 then we can make the coefficients of V3and V1vanish byBy setting ε1= α3/α6
and ε3= −α1/α6,respectively.Scaling V if necessary,we can assume that α6=1.So,V is reduced to the case(ii).
If α6=0,α50 then we can make the coefficients of V2and V1vanish byBy setting ε1= α2/α5and ε2= −α1/α5,respectively.Scaling V if necessary,we can assume that α5=1.So,V is reduced to the case(iii).
If α5= α6=0 then V is reduced to the case(iv).
There is not any more possible cases for investigating and the proof is complete. ?
In the following,we completely determine the Lie invariants and the similarity solutions of the(2D)MKS equation(4)corresponding to the resulted nonclassical symmetries.
(i)For the symmetry operator

the following Lie invariants are resulted:
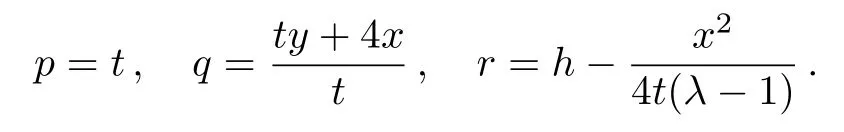
Taking into account the last invariant,we assume a similarity solution of the form:
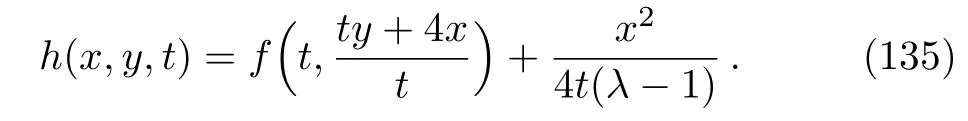
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
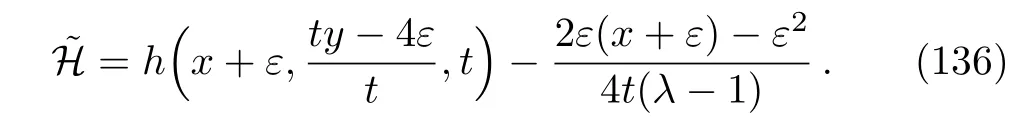
(ii)For the symmetry operator
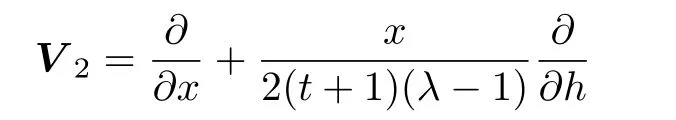
the following Lie invariants are resulted:
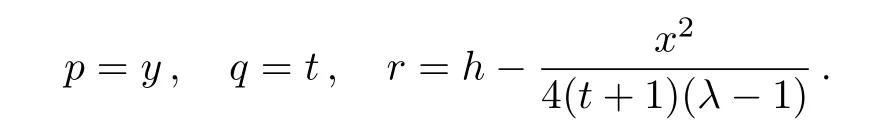
Taking into account the last invariant,we assume a similarity solution of the form:
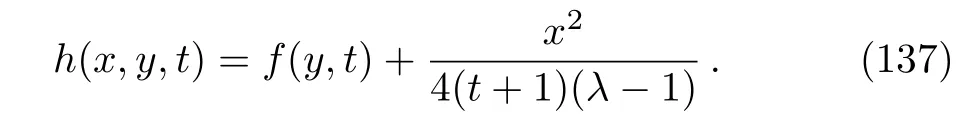
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
(iii)For the symmetry operator

the following Lie invariants are resulted:
Taking into account the last invariant,we assume a similarity solution of the form:
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
(iv)For the symmetry operator
the following Lie invariants are resulted:

Taking into account the last invariant,we assume a similarity solution of the form:
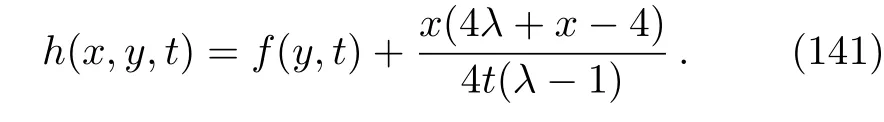
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
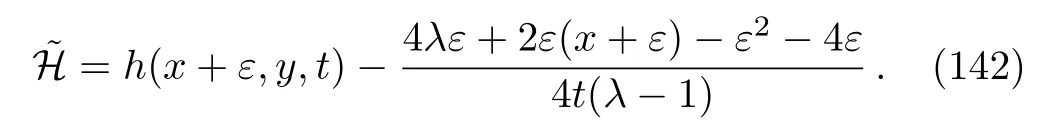
(v)For the symmetry operator
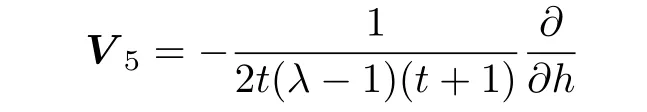
the following Lie invariants are resulted:
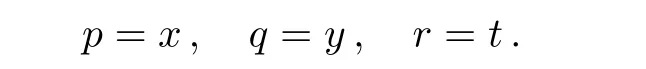
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
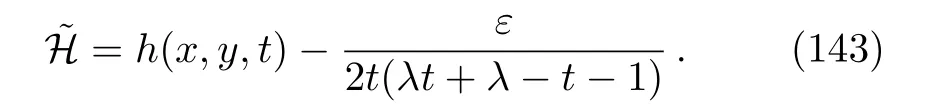
(vi)For the symmetry operator X6= −(2/t2(λ −1))(∂/∂h)
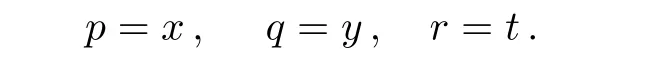
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:

(vii)For the symmetry operator
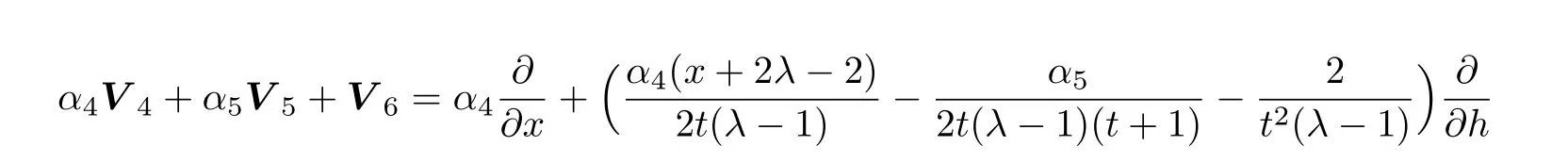
the following Lie invariants are resulted:
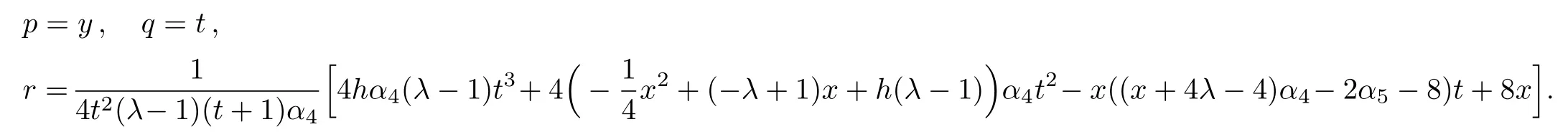
Taking into account the last invariant,we assume a similarity solution of the form:

Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:

(viii)For the symmetry operator

the following Lie invariants are resulted:
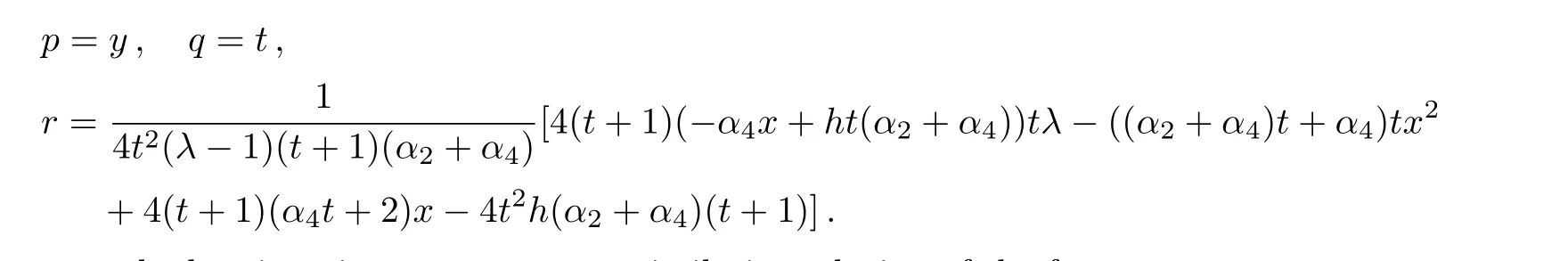
Taking into account the last invariant,we assume a similarity solution of the form:
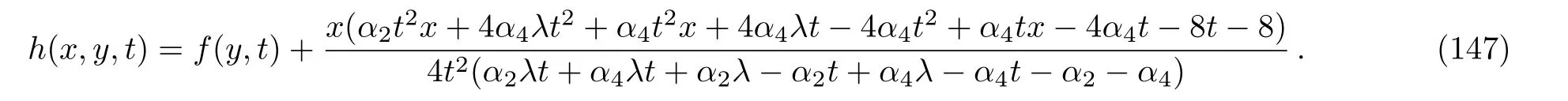
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
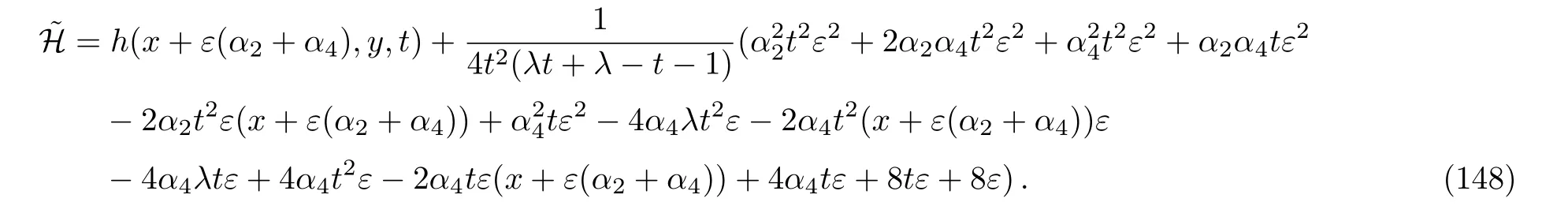
(ix)For the symmetry operator
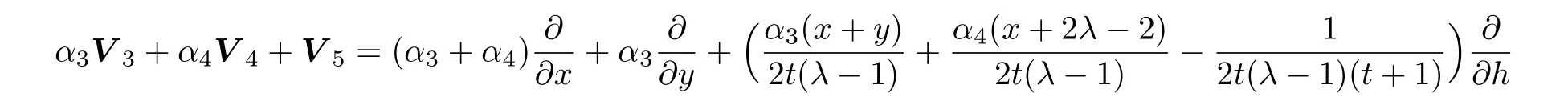
the following Lie invariants are resulted:
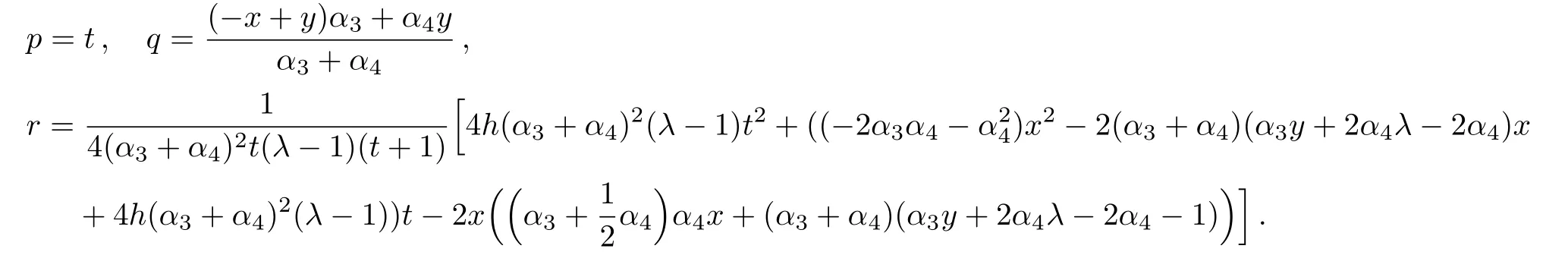
Taking into account the last invariant,we assume a similarity solution of the form:
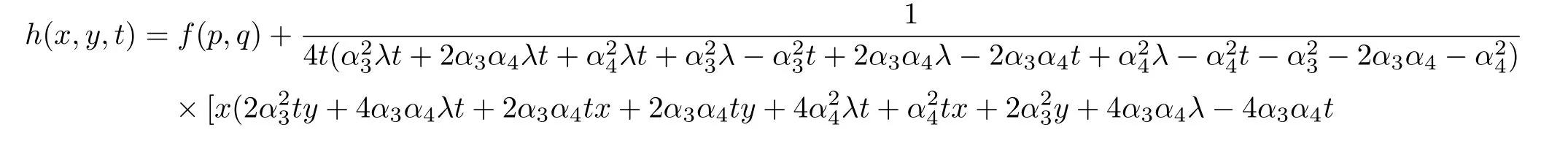
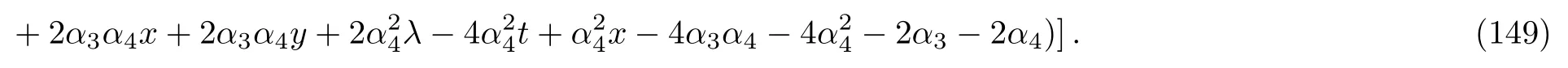
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
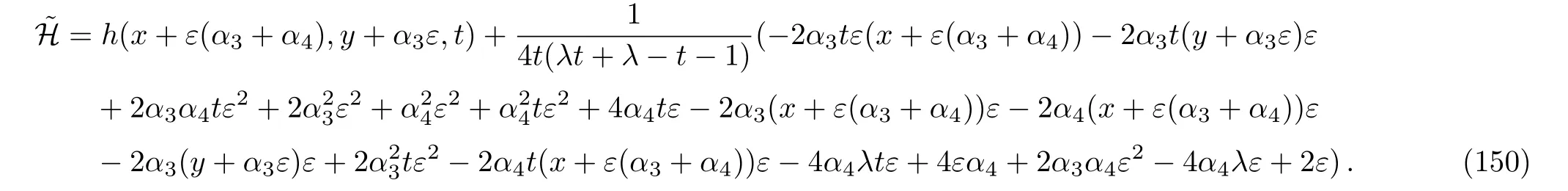
(x)For the symmetry operator
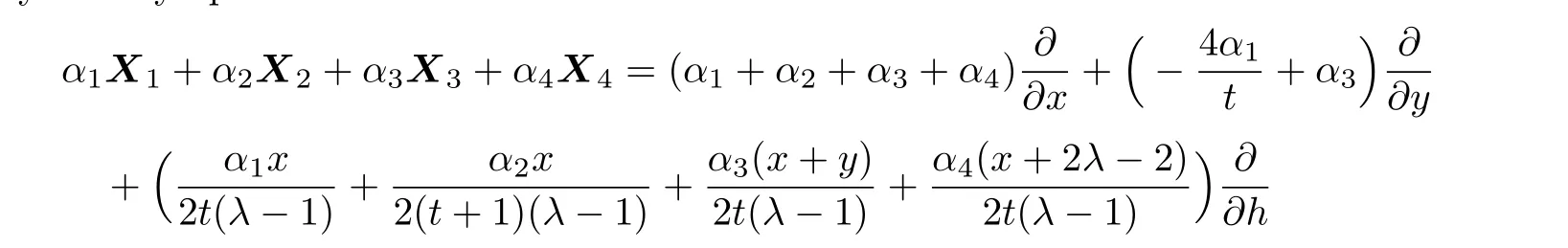
the following Lie invariants are resulted:
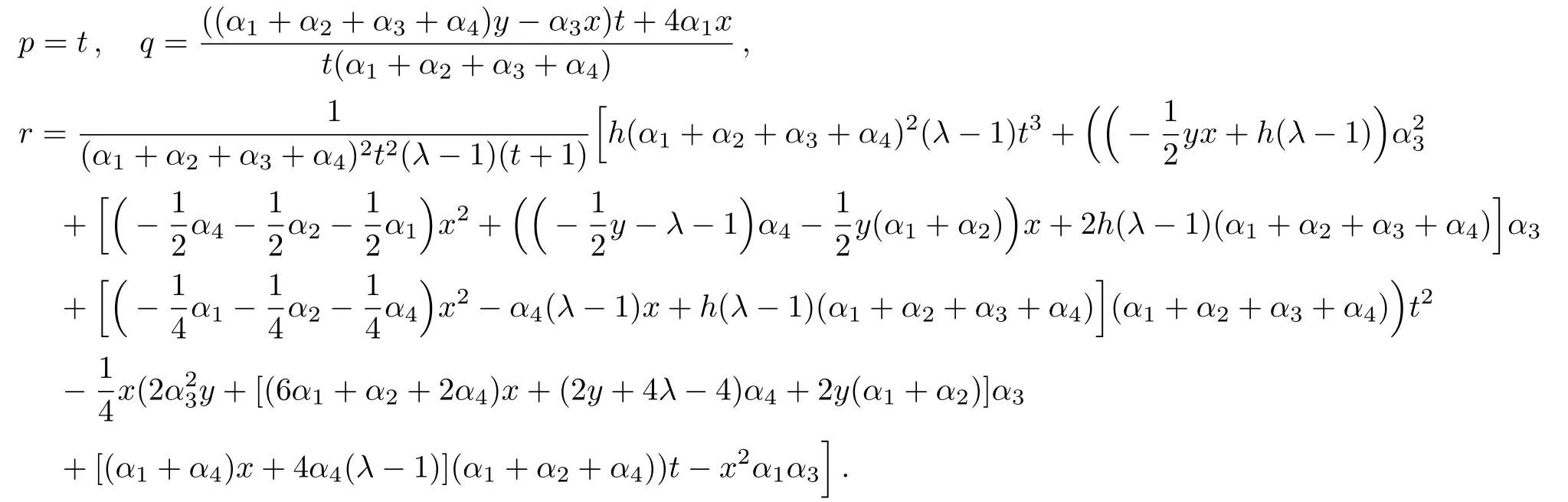
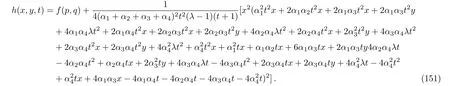
Considering the fact that generally to each one parameter subgroups of the full symmetry group of a system,there will associate a family of solutions called invariant solutions,it is deduced that if H=h(x,y,t)is a solution of Eq.(4),so is the function:
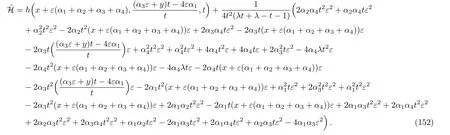
Taking into account the last invariant,we assume a similarity solution of the form:
6 Conclusion
Problems of thermodynamic phase transition are considerably common in nature and applied today in many technologies such as solidification and combustion.The dynamics can be modeled by an interface motion whenever the transition region between two locally stable phases is narrow enough.Reducing the PDEs determining the constituents in each phase to a straightforward equation of motion for an interface can be regarded as one of the constructive procedures of attack for these problems.Particularly,if the system is isotropic,it is practicable to suppose that the normal velocity of the interface relies on only local geometrical characteristics such as curvature.In this paper,we have comprehensively analyzed the invariant solutions of a modified Kuramoto-Sivashinsky equation in two spatial and one temporal dimensions.This well-known nonlinear partial differential equation was first introduced by Bern off and Bertozzi[5]and asymptotically characterizes near planar interfaces,which are marginally long-wave unstable.The classical symmetries of the(2D)MKS equation are computed by applying the criterion of invariance of the equation under the infinitesimal prolonged infinitesimal generators.The structure of the Lie algebra of symmetries of the(2D)MKS equation g is discussed.It is proved that g is a solvable non-semisimple Lie algebra and has two abelian subalgebras where one of them is an ideal in g.The one-parameter groups and symmetry transformations associated to infinitesimal symmetries are determined.Also,the optimal system of subalgebras,which provides the preliminary classification of group invariant solutions is constructed.It is shown that g has no fourdimensional subalgebra.Mainly,the group invariant solutions and the corresponding similarity reduced equations associated to infinitesimal symmetry generators are computed.Finally,the nonclassical symmetries of the(2D)MKS equation are investigated.It is worth mentioning that during our thorough analysis of nonclassical symmetries,we have obtained some new infinitesimal symmetry generators,which were not resulted via the classical method.These resulted symmetries lead to new invariant solutions of our analyzed model,which are not obtainable through the classical procedure.
[1]E.Ben-Jacob,N.Goldenfeld,J.S.Langer,and G.Schrn,Phys.Rev.A 29(1984)330.
[2]J.S.Langer,Lectures in the Theory of Pattern Formation,Chance and Matter,des.by J.Souletie,J.Vannimeus,and R.Stora,Elsevier Science Publishers,Amesterdam(1987).
[3]R.C.Brower,D.A.Kessler,J.Koplik,and H.Levine,Phys.Rev.Lett.51(1983)1111.
[4]R.C.Brower,D.A.Kessler,J.Koplik,and H.Levine,Phys.Rev.A 29(1984)1335.
[5]A.J.Berno ffand A.L.Bertozzi,Physica D 85(1995)375.
[6]M.L.Frankel,Math.Modelling Num.Anal.23(1989)283.
[7]M.L.Frankel and G.I.Sivashinsky,J.Physique.48(1987)25.
[8]M.L.Frankel and G.I.Sivashinsky,Physica D 30(1988)28.
[9]M.L.Frankel,Phys.Lett.A 128(1988)57.
[10]D.C.Sarocka and A.J.Berno ff,Physica D 85(1995)348.
[11]A.Umantsev and S.H.Davis,Phys.Rev.A 45(1992)7195.
[12]Y.Kuramoto,Chemical Oscillations,Waves,and Turbulence,Springer,Berlin,Heidelberg(1984).
[13]G.I.Sivashinsky,Acta Astronaut.4(1977)1177.
[14]J.L.Hansen and T.Bohr,Physica D 118(1998)40.
[15]H.J.Qi,Y.H.Jin,C.F.Cheng,et al.,Chin.Phys.Lett.20(2003)622.
[16]M.Nadja fi khah and F.Ahangari,Commun.Theor.Phys.56(2011)211.
[17]S.Lie,Arch.Math.6(1881)328.
[18]G.W.Bluman,A.F.Cheviakov,and S.Anco,Application of Symmetry Methods to Partial differential Equations,Springer,New York(2010).
[19]A.Kushner,V.Lychagin,and V.Rubstov,Contact Geometry and Nonlinear differential Equations,Cambridge University Press,Cambridge(2007).
[20]P.J.Olver,Applications of Lie group to Diferential Equations,Springer,New York(1986).
[21]P.J.Olver,Equivalence,Invariants and Symmetry,Cambridge University Press,Cambridge(1995).
[22]L.V.Ovsiannikov,Group Analysis of differential Equations,Academic Press,New York(1982).
[23]H.Stephani,differential Equations:Their Solutions Using Symmetry,Cambridge University Press,New York(1989).
[24]Z.Han and Y.Chen,Commun.Theor.Phys.67(2017)1.
[25]X.R.Hu,Y.Q.Li,and Y.Chen,J.Math.Phys.56(2015)053504.
[26]X.R.Hu,Y.Q.Li,and Y.Chen,J.Math.Phys.57(2016)023518.
[27]L.L.Huang,Y.Chen,and Z.Y.Ma,Commun.Theor.Phys.66(2016)189.
[28]Q.Miao,X.R.Hu,and Y.Chen,Commun.Theor.Phys.61(2014)160.
[29]N.Xiong,Y.Q.Li,J.C.Chen,and Y.Chen,Commun.Theor.Phys.66(2016)1.
[30]G.W.Bluman and J.D.Cole,J.Math.Mech.18(1969)1025.
杂志排行
Communications in Theoretical Physics的其它文章
- Particle Size Influence on the effective Permeability of Composite Materials∗
- Modeling Chemically Reactive Flow of Sutterby Nano fluid by a Rotating Disk in Presence of Heat Generation/Absorption
- Study on the Reduced Traffic Congestion Method Based on Dynamic Guidance Information∗
- New Double-Periodic Soliton Solutions for the(2+1)-Dimensional Breaking Soliton Equation∗
- Electrical Properties of an m×n Hammock Network∗
- Searches for Dark Matter via Mono-W Production in Inert Doublet Model at the LHC∗
