基于模拟退火的改进粒子群算法研究及应用

薛永生，吴立尧

（1.海军装备部飞机办公室，北京100000；2.海军航空大学，山东烟台264001）

文献[9]研究了基于模拟退火混沌粒子群优化的盲检测算法，改进的算法在全局收敛性上有较好的改善。文献[10]根据层次分析法的特点引入了特征粒子来求解判断矩阵排序权重，提出了模拟退火改进粒子群优化算法。文献[11]提出了混沌模拟退火粒子群优化算法，并将其应用于Job Shop调度问题。文献[12]将粒子群算法与模拟退火算法相结合，应用于图像分割问题。文献[13]将GPSO与SA算法相结合形成新的混合算法，前期用GPSO，在GPSO陷入停滞时利用SA算法跳出局部最优寻找全局最优。文献[14]利用SAPSO算法规划无人机三维航迹，改善航迹效果明显。在PID参数整定方面，文献[15]提出了一种改进的粒子群优化分数阶PID参数整定方法，并应用在随动电气伺服控制系统中。文献[16]提出了一种蝙蝠算法整定PID控制参数，较优的系统性能和运算效率。文献[17]提出了一种基于免疫选择粒子群算法，并应用在PID控制器参数整定与自适应中。文献[18]针对工业过程中PID参数整定难问题，提出了基于个性化惯性权重的粒子群算法，优化效果明显。

本文从2个方面对PSO算法进行了改进：一方面从对PSO控制参数进行改进，增加了收缩因子；另一方面，将模拟退火算法与粒子群算法有机结合，该改进算法增强了局部搜索能力，通过仿真模拟对比，证明了混合算法的有效性。利用新混合算法整定PID控制参数，并与标准PSO和Z-N法相比较，优化后的系统性能指标变优。

1 算法分析

1.1 带收缩因子的粒子群算法（CPSO）分析

PSO中粒子的飞行行为类似于鸟类运动，从而使整个粒子群的运动表现出与鸟类觅食类似的特性，进而求解复杂的优化问题，即通过群体中个体之间的协作和信息共享来寻找最优解。粒子群优化算法中的粒子速度和位置更新依赖2点：第一，粒子的个体历史最优值；第二，粒子群中的群体当前最优值。在D维空间中粒子i的速度和位置更新公式为：

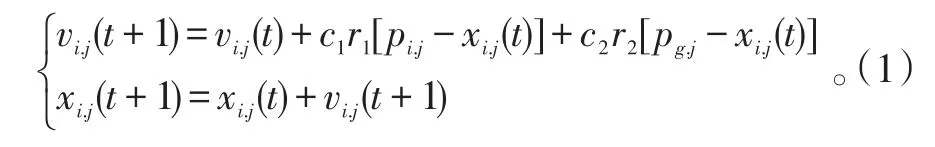
式（1）中：vi.j(t)为粒子的当前速度；xi.j(t)为粒子的当前位置；c1和c2为学习因子；r1和r2为[0，1]之间均匀分布的随机数；pi.j为粒子到目前为止的最优位置；pg.j为所有粒子到目前为止的最优位置。

学习因子c1和c2决定了粒子本身经验信息和其他威力的经验信息对粒子运行轨迹的影响。设置较大c1时，会使粒子过多地在局部范围内徘徊；而设置较大c2值，则会促使粒子过早收敛到局部最小值。通过引入收缩因子，选取合适参数，可确保PSO算法的收敛性，并可取消对速度的边界限制。速度公式为：

式（2）中，φ为收缩因子，且，C=c1+c2。

1.2 模拟退火算法分析

模拟退火算法（SA）是基于Monte-Carlo迭代求解策略的一种随机寻优算法，即通过在搜索区间随机游走，再利用Metropolis抽样准则使随机游走逐渐收敛于局部最优解。Metropolis准则定义了某一温度下系统从状态i变化到状态j的能量概率为：

在图3（c）中，将重心d0（电势待定为v0）作为代理点，用Wi表示子区域d0didi+1的能量（通过v0表示）。通过使得局部能量最小化，可求解下面的等式得到v0。

式（3）中：Ei和Ej为固体在状态i和状态j下的能量；K为波尔兹曼常数。

模拟退火算法可以以一种概率接受“变差的”解，这种行为看似不合理，实则在一定程度上提高了算法的灵活性，扩大了算法的搜索范围，增加了粒子的多样性。这种模拟退火的策略使算法避免在迭代搜索过程中因陷入局部最优解的弊端，提高了搜索到全局最优解的可能性和可靠性。但主要的不足是收敛速度太慢，尤其是问题的规模增大时，算法的效率更是低的令人无法忍受。如此一来，求解问题的近似最优解，需要花费较长时间，如此低的效率致使算法可行性降低，工程价值丧失，因而算法的应用并不广泛。

2 基于模拟退火的改进粒子群算法

为获得更高精度解和更快的收敛速度，基于上述算法得到新的混合算法。新的混合算法在CPSO进化陷入停滞状态时，利用SA算法跳出局部陷阱继续搜索更好的解。SACPSO混合算法基本流程如下。

Step 1：对粒子的位置和速度初始化。确定粒子种群大小N和维数D，设置当前迭代次数和最大迭代次数M。

Step 2：计算每个粒子的适应度，并将当前各个粒子的适应度赋值给pi中，将所有粒子的最优适应度值存储于pg中。

Step 3：判断全局最优值是否停滞或到达指定迭代次数，如果满足转到Step 6。

Step 4：进行下一次迭代计算，若达到最大迭代次数转到Step 6。

Step 5：据轮盘赌策略，从各个粒子中确定全局最优的某个替代值p′g，而后根据下式更新各个粒子的速度与位置。

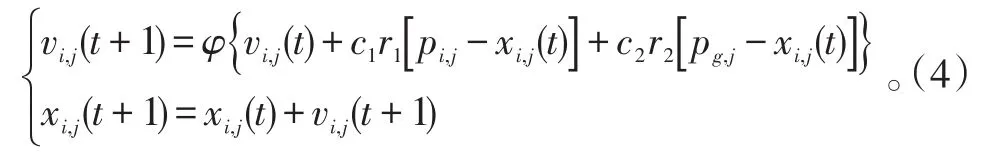
Step 6：设置初始温度和结束温度。

Step 7：在当前温度下，计算各个粒子的适应度值，根据Metropolis准则更新解。

Step 8：根据是否满足停止条件（停止条件一般为预先设定的运算精度或者程序迭代次数），判断是否搜索停止，不满足则转到Step 7。

Step 9：降温，返回Step 7直到得到最优解或达到最低温度。

3 仿真实验及分析

3.1 测试函数

为了证明基于模拟退火的粒子群优化算法的可用性和性能优越性，以及具有较好解决实际问题能力，本文特选出一些经典的标准测试函数进行验证。

1）Ackley函数

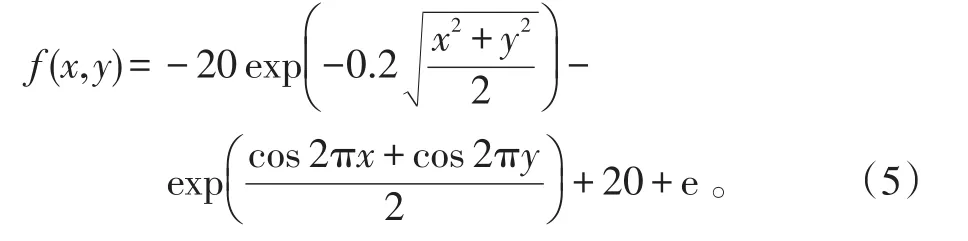
2）Schaffer函数

3）Griewank函数

4）Rastrigrin函数

3.2 优化曲线

优化曲线是使用优化算法获得函数极值的过程描述，下面是利用模拟退火粒子群算法对标准测试函数进行优化的过程，并与传统粒子群算法进行了对比。仿真参数为：N=40，M=200，c1=c2=2.05，λ=0.5。从图1～4结果对比图可知，SACPSO算法随着进化过程的进行，温度逐渐下降，接受差解的概率逐渐减小，从而提高了收敛性能。该算法不仅基本保持了粒子群优化算法的简单、容易实现的特点，而且增强了粒子群优化算法的全局寻优能力，加快了算法的进化速度，提高了收敛精度。仿真结果表明，该算法的性能明显优于传统粒子群优化算法。

图1 Ackley函数适应度曲线对比图Fig.1 Ackley fitness function curve comparison

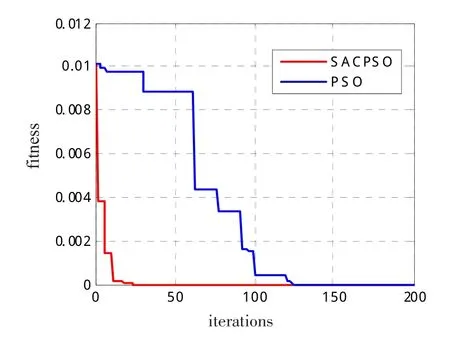
图2 Schaffer函数适应度曲线对比图Fig.2 Schaffer fitness function curve comparison

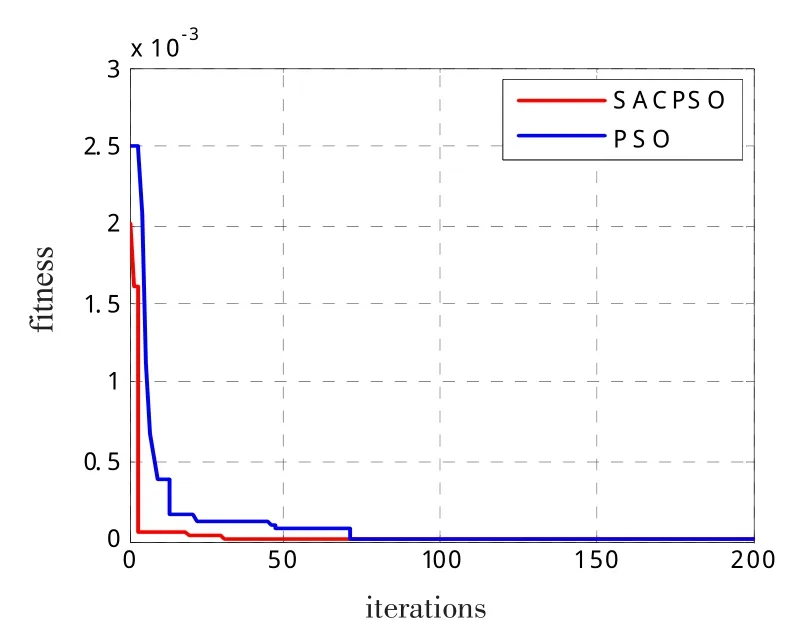
图3 Griewank函数适应度曲线对比图Fig.3 Griewank fitness function curve comparison

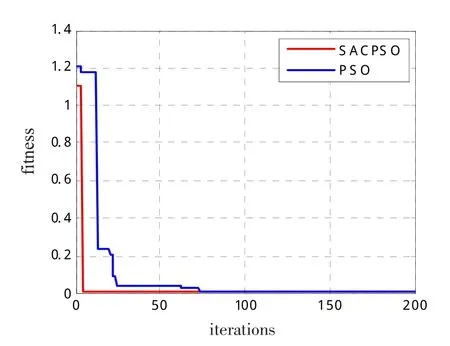
图4 Rastrigrin函数适应度曲线对比图Fig.4 Rastrigrin fitness function curve comparison

4 算法应用

本文针对二阶时滞系统对象，分别利用本文提出SACPSO混合算法、PSO优化算法和Z-N法对PID控制器参数进行整定。选取被控对象的传递函数为：

图5为改进优化算法与传统PID参数整定方法对系统阶跃响应输出对比曲线图。其中，3种方法的超调量分别为0.18%、9.63%和24.99%。由图5可以看出SACPSO算法优化后的系统性能指标最好，标准PSO算法优化后的系统性能指标次之，而Z-N法相对较差。综合上述可得，SACPSO算法用于PID参数整定，不仅系统稳定，而且收敛性能好。

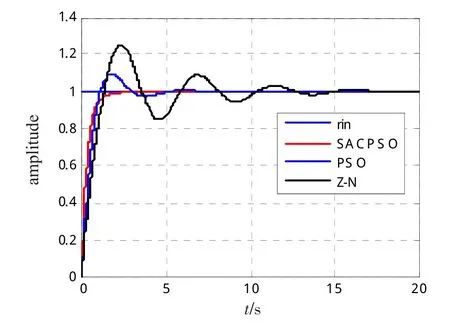
图5 3种算法阶跃响应输出曲线对比图Fig.5 Step response output curve comparison

5 小结

本文对改进粒子群算法的原理、步骤以及测试函数进行了分析和仿真，并将改进算法应用在二阶时滞控制系统PID参数整定问题。本文算法利用模拟退火算法的优势以一定的概率改变粒子的位置更新，使优化进入搜索空间的其他区域进行搜索，这样可以有效地提高粒子群算法跳出局部最优解的能力，从而搜索到函数的全局最优解。仿真分析验证了SACPSO算法的有效性和优越性，用于PID参数整定问题得到很好的效果，优化后的系统性能指标明显优于传统参数整定方法。SACPSO算法结构简单、收敛速度快、收敛性能好等优点可用于工程优化问题。

[1]KENNEDY J，EBERHART R C.Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks.Peth，Australia，IEEE，1995.

[2]KARAKUZU C.Parameter tuning of fuzzy sliding mode controller using particle swarm optimization[J].International Journal of Innovative Computing，Information and Control，2010，6（10）：4755-4770.

[3]ZHANG LEI，GAO SHANG.An image segmentation method based on elite-improved particle swarm optimization[J].Computer applications and Software，2009，26（12）：89-92.

[4]余伟龙，吴庆宪，姜长生.粒子群法在三维航迹规划及优化中的应用[J].电光与控制，2008，15（5）：1-6.YU WEILONG，WU QINGXIAN，JIANG CHANGSHENG.Application of particle swarm algorithm in 3D route planning and optimization of air vehicles[J].Electronics Optics and Control，2008，15（5）：1-6.（in Chinese）

[5]陈冬，周德云，冯琦，等.基于粒子群优化算法的无人机航迹规划[J].弹箭与制导学报，2007，27（4）：340-342.CHEN DONG，ZHOU DEYUN，FENG QI，et al.Route planning for unmanned vehicles based on particle swarm optimization[J].Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（4）：340-342.（in Chinese）

[6]METROPOLIS N，ROSENBLUTH A，ROSENBLUTH M，et al.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics，1953，21（6）：1087-1092.

[7]吴坤鸿，詹世贤.分布式遗传模拟退火算法的火力打击目标分配优化[J].火力与指挥控制，2016，41（3）：89-92.WU KUNHONG，ZHAN SHIXIAN.Optimization for target assignment in fire strike based on distributed genetic simulated annealing algorithm[J].Fire Control and Command Control，2016，41（3）：89-92.（in Chinese）

[8]何庆，吴意乐，徐同伟.改进遗传模拟退火算法在TSP优化中的应用[J].控制与决策，2018，33（2）：219-225.HE QING，WU YILE，XU TONGWEI.Application of improved genetic simulated annealing algorithm in TSP optimization[J].Control and Decision，2018，33（2）：219-225.（in Chinese）

[9]王京，于舒娟.模拟退火粒子群算法的盲检测[J].计算机技术与发展，2011，21（1）：35-37.WANG JING，YU SHUJUAN.Blind detection based on simulated annealing chaotic particle swarm optimization[J].Computer Technology and Development，2011，21（1）：35-37.（in Chinese）

[10]胡建悦，严洪森，刘楠楠.基于模拟退火粒子群算法的AHP排序权值计算[J].计算机技术与发展，2012，22（6）：14-18.HU JIANYUE，YAN HONGSEN，LIU NANNAN.Computing rank weights in AHP of simulated annealing-particle swarm optimization algorithm[J].Computer Technology and Development，2012，22（6）：14-18.（in Chinese）

[11]张捍东，廖天红，岑豫皖.用模拟退火思想的粒子群算法实现图像分割[J].计算机技术与发展，2010，20（5）：83-87.ZHANG HANDONG，LIAO TIANHONG，CEN YUWAN.Image segmentation through particle swarm optimization based on simulated annealing[J].Computer Technology and Development，2010，20（5）：83-87.（in Chinese）

[12]刘爱军，杨育，李斐，等.混沌模拟退火粒子群优化算法研究及应用[J].浙江大学学报，2013，47（10）：1722-1730.LIU AIJUN，YANG YU，LI FEI，et al.Chaotic simulated annealing particle swarm optimization algorithm research and its application[J].Journal of Zhejiang University，2013，47（10）：1722-1730.（in Chinese）

[13]郑申海，胡小兵，郑满满，等.改进粒子群和模拟退火混合算法及其应用[J].计算机技术与发展，2013，23（7）：26-30.ZHENG SHENHAI，HU XIAOBING，ZHENG MANMAN，et al.An improved hybrid algorithm based on particle swarm optimization and simulated annealing and its application[J].Computer Technology and Development，2013，23（7）：26-30.（in Chinese）

[14]唐汇禹，彭世蕤，孙经蛟，等.基于SAPSO算法的无人机三维航迹规划[J].战术导弹技术，2017（2）：62-68.TANG HUIYU，PENG SHIRUI，SUN JINGJIAO，et al.3-D route planning of UAV based on SAPSO algorithm[J].Tactical Missile Technology，2017（2）：62-68.（in Chinese）

[15]高嵩，王磊，陈超波，等.一种改进粒子群优化的分数阶PID参数整定[J].控制工程，2017，24（10）：2010-2015.GAO SONG，WANG LEI，CHEN CHAOBO，et al.An improved particle swarm optimization algorithm for fractional order PID parameter tuning[J].Control Engineering of China，2017，24（10）：2010-2015.（in Chinese）

[16]吕磊，章国宝，黄永明.基于蝙蝠算法的PID参数整定[J].控制工程，2017，24（3）：548-553.LV LEI，ZHANG GUOBAO，HUANG YONMING.BA-based PID tuning method[J].Control Engineering of China，2017，24（3）：548-553.（in Chinese）

[17]邓丽，蒋婧，费敏锐.基于免疫粒子群算法的PID参数整定与自适应[J].自动化仪表，2013，34（2）：65-67.DENG LI，JIANG JING，FEI MINRUI.PID parameters tuning and adaptation based on immunity particle swarm optimization[J].Process Automation Instrumentation，2013，34（2）：65-67.（in Chinese）

[18]杨智，陈颖.改进粒子群算法及其在PID整定中的应用[J].控制工程，2016，23（2）：161-166.YANG ZHI，CHEN YING.Improved particle swarm optimization and its application in PID tuning[J].Control Engineering of China，2016，23（2）：161-166.（in Chinese）