基于中值滤波的口腔CT图像环形伪影去除算法

王闯 李诗 吴少海 彭晓龙 广东省医疗器械质量监督检验所 （广东 广州 510663）

锥束CT系统，采用锥形束X射线和平板探测器，围绕物体进行圆周旋转，采集到的一系列投影数据进行计算机图像重建，得到连续多层CT图像，在口腔临床医学成像方面具有广泛的应用前景和较高的临床意义[1]。然而，平板探测器上分布有按矩阵形式排列的大量探测元，由于加工工艺精度的限制，无法保证它们的响应是一致的，这就导致重建出的CT图像含有以图像中心为圆心的一系列环形伪影，这些伪影降低了图像质量，限制了后期的图像处理精度。

CT图像环形伪影去除算法主要分为两类。第一类是前处理方法，即在投影数据中利用图像识别技术识别出探测器上响应不一致的像素点，然后利用临近的像素点插值得到该像素点的估计值，最后利用CT图像重建算法重建出无环形伪影的CT图像[2-5]。该类方法的难度在于识别探测器像素点和像素点值插值，若处理不当，重建后CT图像中的环形伪影无法全部去除，且部分细节信息被破坏。第二类是后处理方法，即对含有环形伪影的CT图像进行处理[6-8]。一般地，将CT图像从笛卡尔坐标系转换到极坐标系，环形伪影从环形变为直线型，再利用图像直线检测技术和插值/滤波技术对伪影进行定位和信息恢复，最后变换回笛卡尔坐标系，得到最终图像。该类方法由于需要坐标系的变换，而且图像上像素点是离散的，容易造成信息失真。本文旨在提出一种伪影去除效果好且计算复杂度较低的口腔CT图像环形伪影去除算法，提出基于中值滤波的口腔CT图像环形伪影去除算法，实验结果表明，新方法能够在伪影去除和结构信息保持方面取得满意的效果。

1.方法

1.1 一维和二维中值滤波算法

在一维信号处理中，一维中值滤波算法常用来对信号中的突变点进行处理[9]。设一维离散信号为x(i)，则第i个信号点的中值滤波数学公式表示为：

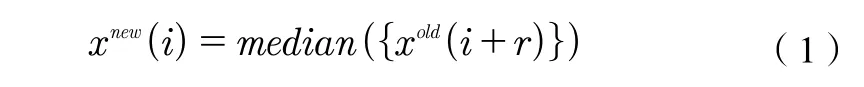
其中，滤波前的信号记为xold，滤波后的信号记为xnew。i表示信号的第i个信号点。r为整数，决定以(i)为中心的矩形窗邻域的范围，其取值范围为-R≤r≤R。median(.)函数表示对xold(i+r)像素点构成的集合进行升或降排序，然后取中值作为xnew(i)。

在二维信号处理（即图像）中，二维中值滤波算法常用来对图像中椒盐噪声进行处理[10]。设一幅图像矩阵为x，则像素点(i,j)的中值滤波数学公式表示为：

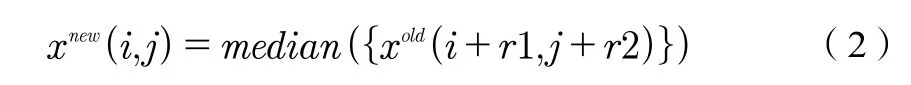
其中，滤波前的图像记为xold，滤波后的图像记为xnew。(i,j)表示图像的第i行第j列的像素点。r1和r2为整数，决定以(i,j)为中心的矩形窗邻域的范围，其取值范围为[-R,R]。median(.)函数表示对xold(i+r1,j+r2)像素点构成的集合进行升或降排序，然后取中值作为xnew(i,j)。图1所示为二维中值滤波示意图，窗宽为3×3，对x1～x9的像素值排序后的中间值，即为最终值。

1.2 中值滤波的使用和不足

将CT图像从笛卡尔坐标系转换到极坐标系，环形伪影从环形变为直线型，若滤除这些直线伪影，一维滤波的游走方向垂直于直线伪影，这等价于未做坐标变换前沿着图像中心向四周进行径向的一维滤波，避免了因坐标系变换带来的信息失真问题。实验发现这种处理方法有效去除了环形伪影，但其他的正常结构边缘容易产生“毛刺”效应。

对CT图像直接进行二维中值滤波，正常结构边缘得到比较好的保持，但是环形伪影不能得到完全消除。

1.3 本文方法

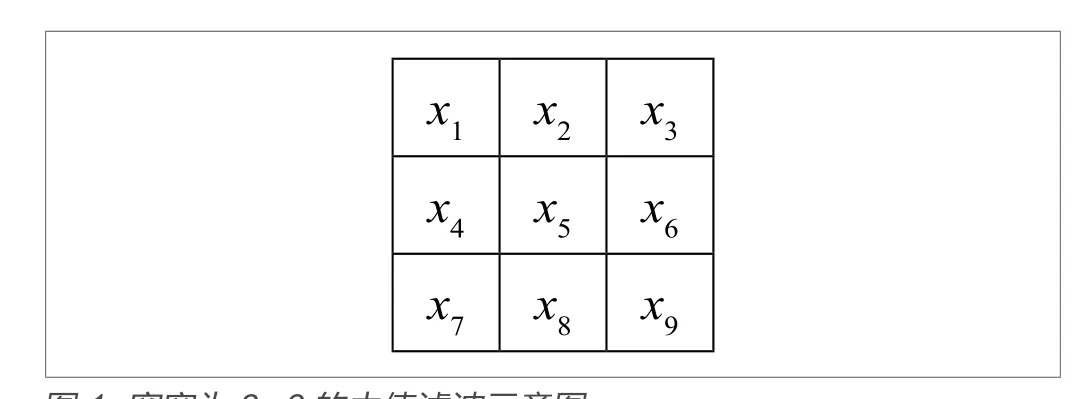
图1.窗宽为3×3的中值滤波示意图

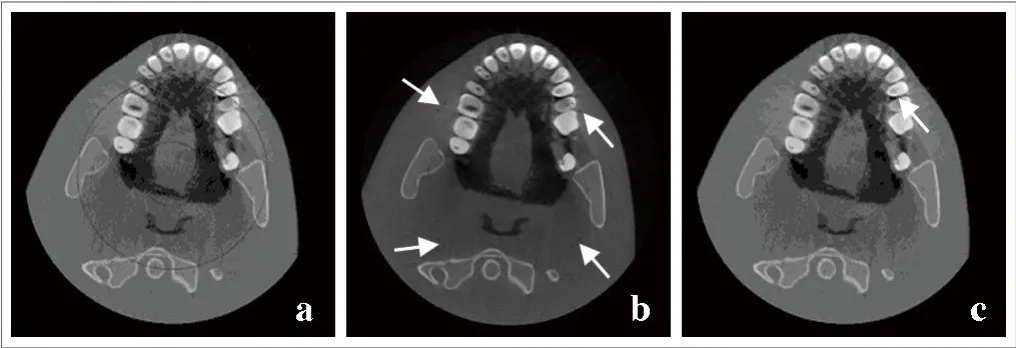
图2.带有环形伪影的CT图像和二维中值滤波结果

鉴于一维和二维中值滤波去除环形伪影和正常结构边缘保持的利弊，融合各自优点形成无伪影且正常信息结构得以保持的CT图像，提出如下方法：

①输入带有环形伪影的口腔CT图像；

②对①中图像进行一维中值滤波处理得到图像A；

③对①中图像进行二维中值滤波处理得到图像B；

④用图像A减去图像B，得到差值图像Idiff；

⑤对图像Idiff进行归一化处理，使图像中的每个像素值范围在0～1：

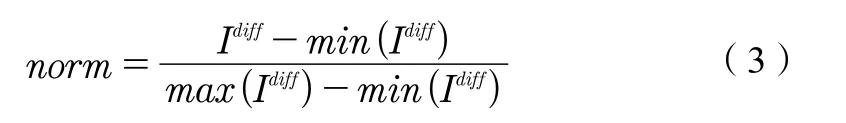
⑥计算权重因子：

⑦对图像A和B加权求和，得到最终图像I new：

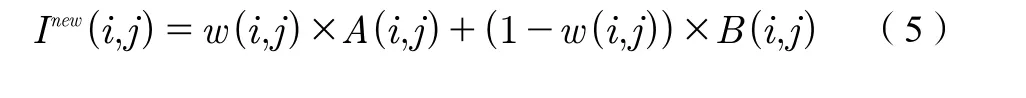
2.实验

实验环境为CPU：Intel®Core™i3-4160，内存：5.0G，操作系统为Windows 10 64bits，编程软件：Matlab 2009。实验数据为广州华端科技有限公司的口腔CT系统拍摄的头部模型CT图像，仿真产生两圈明显的环形伪影，见图2a。

图2b为窗宽为3×3的二维中值滤波处理结果，可见，图中多处箭头处仍含有残留的环形伪影；图2c为窗宽为5×5的二维中值滤波处理结果，虽然较图2b有更明显的改善，但图中箭头处的残留伪影仍然无法去除，采用更大的窗宽同样无法去除。

图3a是窗宽为3的一维径向中值滤波处理结果，环形伪影得到完全的去除，但是对于骨组织的边缘结构处出现了明显的“毛刺”结构，如图3a箭头处，放大图更显而易见；图3b是窗宽为5的一维径向中值滤波处理结果，环形伪影完全消除，但是如图中箭头所示的骨组织的边缘发生了像素值的改变，表现为骨线不连续，这是因为在一维径向中值滤波处理中，误将骨线当作伪影线进行处理，且窗宽更大其效应越严重。图3c是利用本文方法处理得到的结果，参数a=0.4，可见，综合了图2c与图3a的各自优势融合成无伪影且边缘结构组织得到有效保持的CT图像。

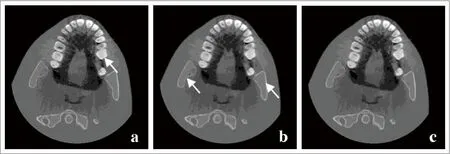
图3.一维中值滤波结果和本文方法处理结果

3.结语

本研究在一维和二维中值滤波处理含有环形伪影的口腔CT图像基础上，通过引入权重函数模型，结合不同滤波手段后的图像的优势，融合成为无环形伪影且边缘结构组织得到有效保持的CT图像。方法通过口腔CT图像数据进行了证实，能够得到满意的效果，证明该算法的可行性。

[1]Jaffray DA, Siewerdsen JH.Cone-beam computed tomography with a flat-panel imager: initial performance characterization[J].Medical physics,2000,27(6):1311-1323.

[2]郭宏,曾栋,张华,等.基于投影域小波滤波处理的CT图像环形伪影去除方法[J].南方医科大学学报,2015,35(9):1258-1262.

[3]余晓锷,罗君芳,陈武凡.基于弦图的CT图像环形伪影校正[J].医学争鸣,2009,30(3):207-209.

[4]王珏,黄苏红,蔡玉芳.改进Canny算法的CT图像环形伪影校正[J].光学精密工程,2011,19(11):2767-2773.

[5]王珏,黄苏红,蔡玉芳.工业CT图像环形伪影校正[J].光学精密工程,2010,18(5):1226-1233.

[6]齐宏亮,洪虹,徐圆,等.一种快速去除CT环形伪影的方法[J].南方医科大学学报,2012,32(12):1748-1751.

[7]杨俊,甄鑫,卢文婷,等.基于圆扫描轨迹的锥形束CT重建与环形伪影消除[J].南方医科大学学报,2009,29(12):2379-2382.

[8]Kyriakou Y, Prell D, Kalender WA.Ring artifact correction for high-resolution micro CT[J].Physics in Medicine & Biology,2009,54(17):N385.

[9]Veiga AL, Grunfeld CM.Hardware implementation of a single-cycle one-dimensional median filter[C].Circuits & Systems.IEEE,2015:1-4.

[10]Huang T, Yang G, Tang G.A fast two-dimensional median filtering algorithm[J].IEEE Transactions on Acoustics Speech & Signal Processing,1979,27(1):13-18.