一种基于神经网络的土壤湿度预测方法
2018-06-07杨晓霞张承明
杨晓霞, 贾 嵩, 张承明, 程 清, 张 航
(1.山东农业大学信息科学与工程学院,山东泰安 271018; 2.山东省数字农业工程技术研究中心,山东泰安 271018;3.中国联通有限公司泰安市分公司,山东泰安 271000)
土壤湿度是陆地和大气能量交换过程中的重要因子,在农业中扮演着关键的角色[1]。作为植物生长必不可缺的养料[2],土壤湿度是主导农作物长势及产量的最重要的因素之一,因此高质量的土壤湿度时序预测是指导农业生产的基本要求。
在时间序列数据预测方面,国内外学者做了大量的研究工作,提出了很多不同的预测方法。这些方法可以分为物理方法、统计学模型和人工智能方法等,不同方法各有其适用场合。物理学方法利用相关量进行时间序列预测,例如利用降水、径流、温度等物理量预测土壤湿度,李雨鸿等利用土壤湿度与气象因子、环流因子相关关系,甄选土壤相对湿度主要影响因子,建立回归方程预测土壤湿度,模型预测精度达到80%[3];孙倩倩等基于东北地区近30年土壤湿度观测资料,采用CAST聚类方法进行土壤湿度区划,对各区域土壤湿度的时空变化特征展开分析,通过筛选对土壤湿度影响显著的关键因子,并利用他们建立多元线性回馈方程建立土壤湿度分区预报模型,该模型的预测误差低于13%[4]。这种物理学方法的预测依赖于与土壤湿度相关的数据,这些数据往往种类很多,并且有些数据难以获取。Ren等提出物理学模型的输出结果往往可以作为统计学模型的辅助输入数据[5]。统计学方面在描述历史数据之间的关联时,AR、ARMA、ARIAM、SARIMA等模型都被用于时间序列预测[6-12]。这些基于统计学的时间序列预测方法往往假设时间序列数据之间存在线性相关的关系。但是土壤湿度时间序列数据具有非线性的特点,利用统计学模型难以得到较高的预测精度[13-15]。
为了克服这一问题,人工智能的方法越来越多地被使用到时间序列预测当中[16-20],Ho等将神经网络模型与ARIMA模型同时用于时间序列模型预测,结果显示在时间序列分布随机和非线性情况下,神经网路模型比ARIMA模型拥有更好的预测精度[19]。Li等利用feed-forward ANN模型进行时间序列预测,并与ARIMA预测结果进行比较,结果显示ANN预测结果精确度更高[20]。
作为人工神经网络的典型,由于BP神经网络具有良好的非线性映射能力而被广泛地应用于时间序列预测中[21-26]。Yang等[21]和Wang等[22]利用BP神经网络对时间序列数据进行预测,并且都得到了理想的预测结果。BP模型的预测精度及训练时间往往依赖于其初始权值和阈值的选定,而在标准BP算法中初始权值和阈值是随机设置的。为了克服BP算法的这一缺点,一些启发式的算法例如遗传算法(GA)、粒子群算法和蚁群算法等往往用于进行BP初始权值和阈值的优化。Zhang等使用GA优化BP神经网络的初始权值和阈值,然后利用BP网络预测激光焊接时的焊接外观,试验结果表明经过GA优化之后的BP网络的预测精度比标准BP网络提高10%[23]。Zhen等首先使用PSO优化BP神经网络的初始权值和阈值,然后利用优化后的BP神经网络进行高速铣削力建模,与标准BP相比,经过PSO优化后的BP的训练时间减少,并且预测精度增加[24]。
本研究将提出一种将BP神经网络和PSO相结合的新型土壤湿度预测方法,针对BP和PSO的局限性,提出2种算法的改进方法并用于预测。以“渤海粮仓”山东试验区东营市垦利县20个观测站点2013—2014年的土壤湿度时序数据为对象进行了试验,并在同组数据上分别使用不同预测方法进行对比试验,验证文章所提出方法的有效性。
1 试验区概况和数据预处理
1.1 试验区概况
2013年我国启动“渤海粮仓”农业科技工程,计划通过对环渤海地区266.7万hm2中低产田和66.7万hm2盐碱荒地的改造,实现到2017年增粮30亿kg,到2020年增粮50亿kg的目标,将长期遭受旱涝碱灾害的环渤海地区建成我国重要的“粮仓”,图1为渤海粮仓山东项目区示意图,其中黑色框内是本研究区。本研究选择“渤海粮仓”山东项目区的东营市垦利县作为试验区,该试验区位于山东省东北部黄河三角洲的黄河最下游入海口处。其位置为37°24′~38°10′N,118°15′~119°19′E。试验区地处温带季风气候区,冬季干冷,夏季湿热,四季分明,平均降水为547.2 mm/年,其中夏季占67.8%,冬季仅占3.6%。该地区有潮土和盐渍土2大土壤类型,质地偏轻、养分贫乏、盐碱较重,是我国重要的盐碱荒地改造区。
1.2 数据获取
时间序列数据由试验区布设的监测点产生,试验区内共布设了10个监测点,图2是试验区及监测点布设情况,10个监测点的土壤类型均为盐渍土。每个监测点的观测频率为 1 h/次。文章选取监测点2013年1月1日至2014年12月31日的数据,共计175 200条数据记录。

1.3 数据预处理
由于传感器故障或者传输原因,在某些监测点的数据中存在有一小部分缺失数据,其值为0(数据缺省值),这些数据会影响预测精度。针对这些缺失数据,利用欧氏距离选择同一个监测点上最接近的前后6组数据进行加权平均。
Dk=ωk+3Dk+3+ωk+2Dk+2+ωk+1Dk+1+ωk-1Dk-1+ωk-2Dk-2+ωk-3Dk-3。
(1)
式中:Dk为缺失数据,Dk+i表示时间上滞后Dk的数据,Dk-i表示时间上超前Dk的数据,ωk-3为相应权值,在本研究的处理过程中取所有ω相等(1/6)。
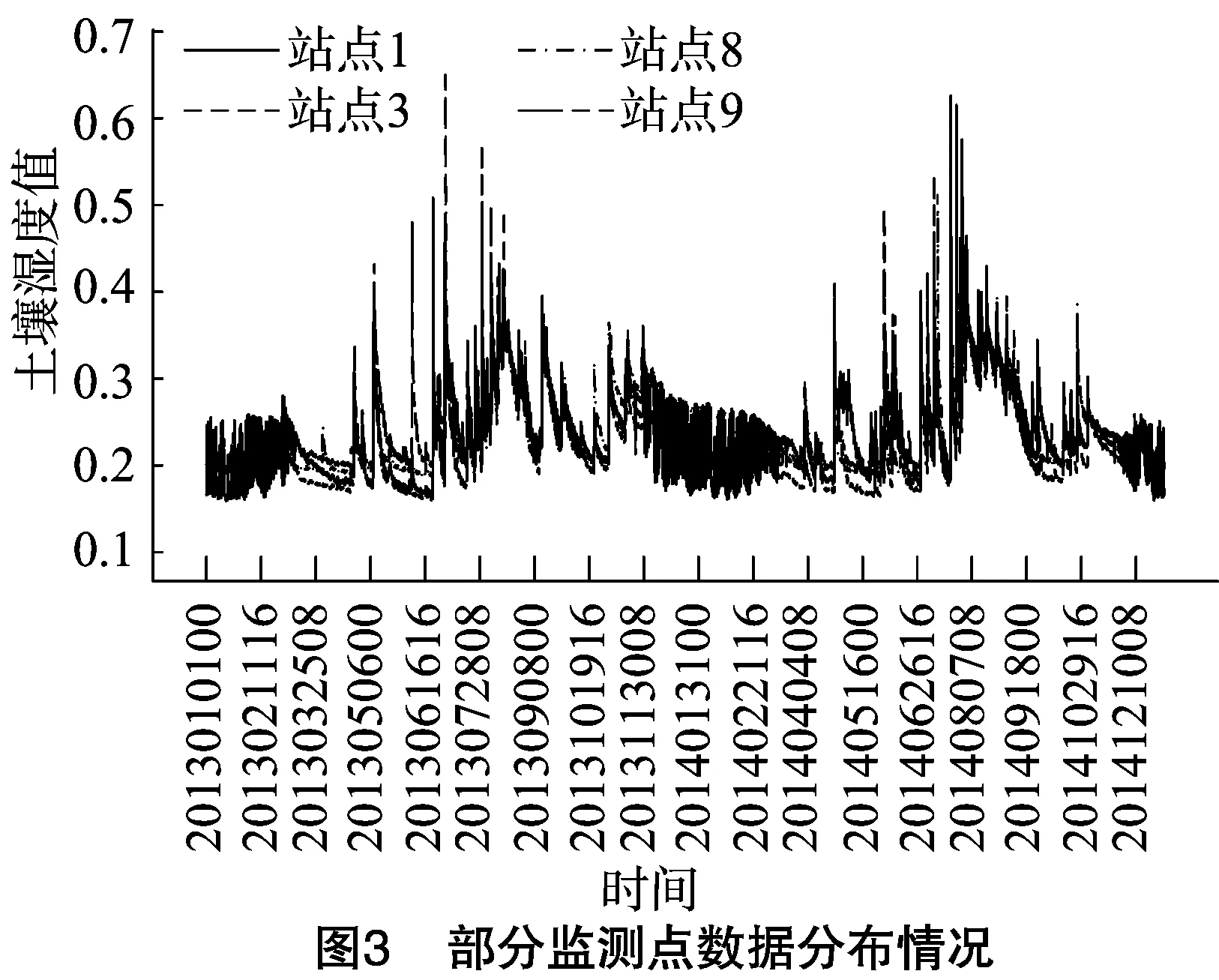
得到10组时间序列数据,利用统计学方法对10个监测点数据做分布特性分析,图3为监测点1、3、8、9的观测数据分布情况。从图3可以看出4个监测点数据的分布大致相同,进一步将10个观测点同一时刻数据取算数平均,得到 17 520 条时间序列数据,将这些数据作为试验数据进行预测方法的研究。
2 预测模型建立
图4为预测流程,首先确定BP神经网络结构,然后利用PSO进行初始权值和阈值的优化,最终训练网络并得到最终预测结果。

2.1 BP神经网络参数设计
2.1.1 网络层次 根据Kolrnogorov’s定理,一个3层BP神经网络能够实现对任意非线性函数进行逼近,所以本研究选取3层BP神经网络进行土壤湿度预测研究,也就是网络中包含1个隐含层。
2.1.2 输入层、输出层和隐含层结点的确定 这里将网络输出层结点数量确定为1个。Liu等提出ARIMA模型的参数估计过程中利用自相关函数ACF、偏自相关函数PACF等,可以用于神经网络输入层节点数量的确定[11]。依据该方法首先分析各子序列的ACF和PACF,并得到输入层节点数目。隐含层节点的选取,依据Hecht-Nelson’s方法:如果输入层节点数目为n,则隐含层节点数目为2n+1。这样最终确定输入层节点数目为7个,输出层节点数目为1,隐含层节点数据为15。
2.2 利用PSO优化BP初始权值和阈值
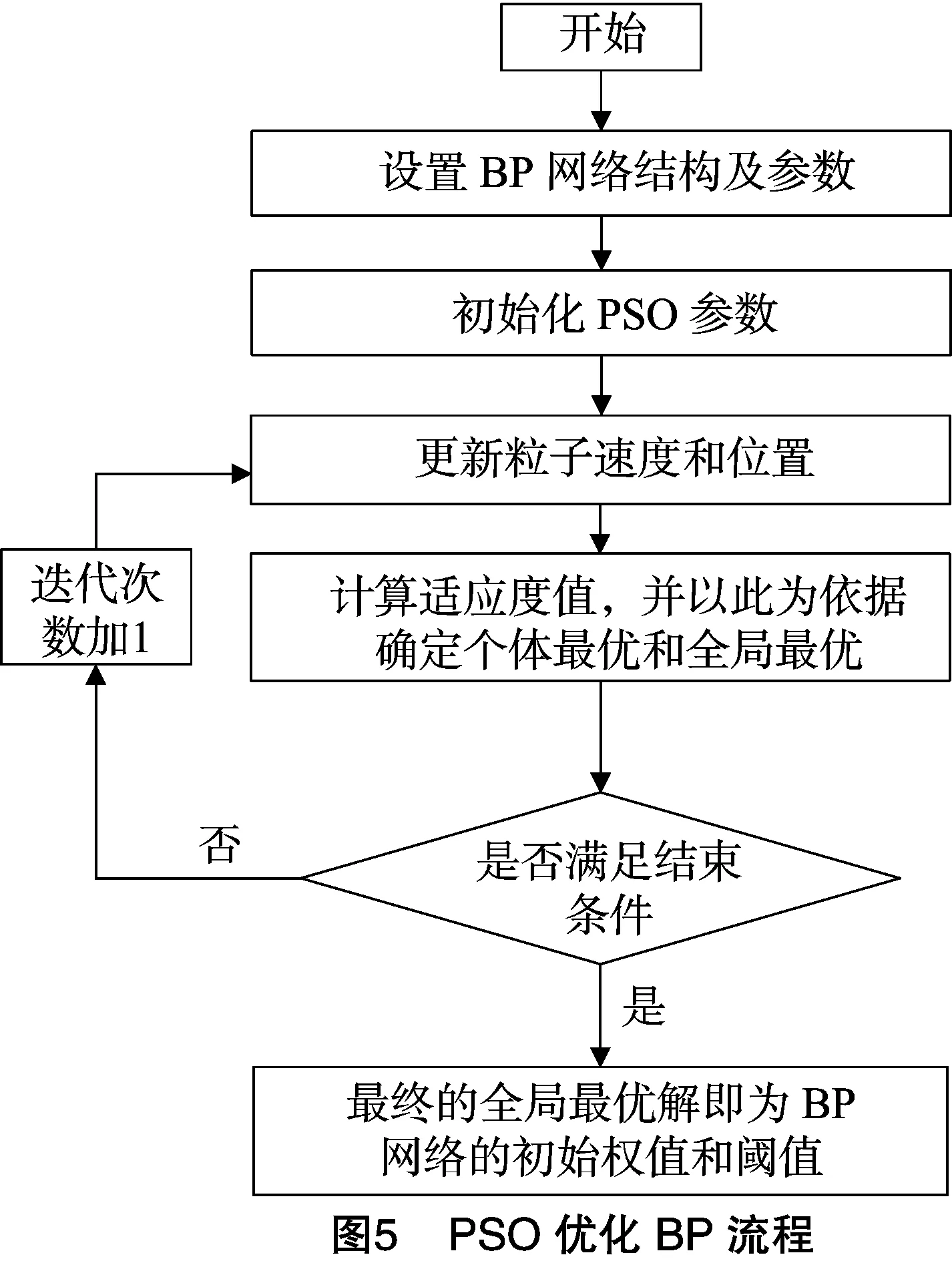
图5为PSO优化BP的流程,初始化PSO算法参数,更新速度和位置2个变量,利用适应度值确定个体最优和全局最优,然后迭代计算,直到满足精度要求。
在标准粒子群算法中采用公式(2)和(3)进行粒子速度和位置的更新。
vid(t+1)=ωvid(t)+c1r1[pid-zid(t)]+c2r2[pgd-zid(t)];
(2)
zid(t+1)=zid(t)+vid(t+1)。
(3)
式中:vid(t+1)和zid(t+1)分别为粒子i第(t+1)次迭代之后的速度和位置,pid和pgd分别为迭代到目前为止粒子i的个体最优解和种群最优解。c1和c2为加速常数,r1和r2为随机数。ω表示惯性权重,在标准粒子群算法中取线性递减的惯性权重[公式(4)],其中ωmax和ωmin分别表示惯性初值和惯性终值,iter表示当前迭代次数,itermax表示最大迭代次数。
(4)
在标准粒子群算法中,由于ω取线性递减,且c1和c2取值为常数,这些不满足学习过程特点,导致在迭代过程中(尤其是迭代后期)收敛速度慢且易陷入局部最优解[27-28]。
在粒子群算法中ω决定了算法的搜索能力,c1和c2分别决定了自我学习和种群学习能力。适应度值是评价算法解的“好坏”的标准,适应度值较大的粒子质量较差,反之粒子的质量较好。按照粒子群算法的特点,在迭代初期应当有较强的搜索能力、较大的自我学习能力和较小的种群学习能力。而在迭代后期则相反。同时当粒子质量较差的时候,应当具有较强的搜能力和种群学习能力,此时的自我学习能力应当适当减弱,在粒子质量较好的情况下,则需要增强粒子的自我学习能力,减弱搜索能力和种群学习能力。
本研究提出一种将适应度值与迭代次数相结合优化ω、c1和c2的方法[公式(5)],根据粒子的适应度值求出所有粒子的适应度平均值fA。根据该值将粒子分为f>fA和f (5) 标准BP算法采用梯度下降依次修正各层权值。即 ωij(t+1)=ωij(t)+Δωij(t); (6) ωij(t+1)=φij(t)+Δφij(t)。 (7) 在上述公式中可以看出,η一旦设定之后在整个学习过程中不会发生变化,如果η设置过大会导致网络错过最优解,而η设置过小则网络迭代速度慢且易陷入局部最优。并且在学习过程中,如果误差曲面存在极值点,Δωij或者Δφij为0,ωij(t+1)=ωij(t)或者φij(t+1)=φij(t),此时网络容易陷入局部最优值而停止学习。基于这些问题,首先利用动量因子将公式(6)和(7)修改如下: ωij(t+1)=ωij(t)+(1-α)Δωij(t)+αΔωij(t-1); (8) φij(t+1)=φij(t)+(1-α)Δφij(t)+αΔφij(t-1)。 (9) 从式(8)和(9)中可以得到,当α=0时,权值的变化完全与标准BP算法中权值修改一致;当α=1时,新的权值变化等于前一次权值的变化。通过α的调整,可以减少网络训练时的震荡现象,避免网络陷入局部最优。同时在学习过程中自适应的调整学习率,当新的调节误差比设定的最大调节误差大时,将η降低,即将上一步η乘以一个小于1的系数,并将α置0;当新的调节误差比上一步调节误差小时,用η乘以一个大于1的值增加其大小。这样在确保迭代速度的同时,有效避免网络陷于局部最小值。 为验证研究提出方法的有效性,笔者进行了另外4种方法的对比试验,5种方法分别为BP、PSO-BP、IPSO-BP、PSO-IBP、IPSO-IBP。其中BP是利用神经网络直接对时间序列进行预测;PSO-BP利用PSO优化BP网络初始权值和阈值,再用BP进行时间序列数据的预测;PSO-IBP利用PSO优化BP网络初始权值和阈值,再用改进的BP进行时间序列数据的预测;IPSO-BP首先对PSO进行优化,然后利用优化后的PSO优化BP网络初始权值和阈值,最后用BP进行时间序列数据的预测;IPSO-IBP首先对PSO进行优化,然后利用优化后的PSO优化BP网络初始权值和阈值,最后用改进的BP进行时间序列数据的预测。表1为5种方法描述对比结果。在5种不同的方法中,BP网络结构完全相同,并且采用相同的针对于PSO和BP的改进方法。 表1 5种方法描述对比 图6为5种方法预测结果对比,横轴为迭代次数,纵轴为预测结果的均方误差(mean squared error,MSE)(由于数据较小,MSE经过自然对数转换)。5种方法中标准BP的MSE最高为3.57×10-5,在迭代30次时MSE迅速降低,然后在55次迭代、80次迭代和110次迭代时MSE分别降低,最终在110次迭代时降低至最低值。PSO-BP方法在迭代60次左右MSE达到稳定,在80次迭代时经过小幅度降低至最低值 3.16×10-6,经过PSO优化之后的预测结果明显好于标准BP网络的结果。PSO-IBP和IPSO-BP方法最低MSE与PSO-BP方法较为接近,但是从图中可以看到,PSO-BP方法在60次迭代后MSE达到基本稳定,而PSO-IBP和IPSO-BP方法都在20次迭代时迅速达到MSE的最低值,说明后2种方法有更快的收敛速度。IPSO-IBP方法在10次迭代时迅速降低至MSE最低值1.01×10-9,然后一直保持稳定,可以看出IPSO-IBP方法具有更小的预测误差。 由图7可以看出,BP方法在120次迭代之后运算结束,PSO-BP方法迭代次数为82次,PSO-IBP方法迭代次数28次,IPSO-BP方法迭代24次,IPSO-IBP方法迭代14次。本研究所提出的方法能有效减少迭代时间,提高运行效率。 本研究提出了一种将离散小波变换、PSO和BP相结合的土壤湿度时间序列预测方法,针对土壤湿度时间序列的非平稳性,首先利用离散小波变换将其分解为若干个相对平稳的自序列,再用改进后的神经网络对各子序列分别进行预测,最后重构得到预测结果。针对BP神经网络收敛速度慢、易陷入局部最优的问题,提出利用PSO算法优化BP网络的初始权值和阈值,同时提出了针对PSO收敛速度慢和易陷入局部最优等问题的改进方法。试验结果表明,此方法能有效减少迭代次数,提高预测精度。 参考文献: [1]Qiu J X,Gao Q,Wang S,et al.Comparison of temporal trends from multiple soil moisture data sets and precipitation:the implication of irrigation on regional soil moisture trend[J]. International Journal of Applied Earth Observation and Geoinformation,2016,48(4):17-27. [2]Nunzio R. Soil moisture at local scale:measurements and simulations[J]. Journal of Hydrology,2014,516(6):6-20. [3]李雨鸿,李倩倩,李 辑,等. 东北地区春播期土壤水分预测方法研究[J]. 干旱地区农业研究,2013,33(6):178-183. [4]孙倩倩,刘晶淼,梁 宏,等. 东北地区土壤湿度的区域性预报模型研究[J]. 自然资源学报,2014,29(6):1065-1075. [5]Ren C,An N,Wang J,et al. Optimal parameters selection for BP neural network based on particle swarm optimization:a case study of wind speed forecasting[J]. Knowledge-Based System,2014,56(3):226-239. [6]Tascikaraoglu A,Uzunoglu M. A review of combined approaches for prediction of short-term wind speed and power optimal parameters selection for BP neural network based on particle swarm optimization:a case study of wind speed forecasting[J]. Renew and Sustain Energy Reviews,2014,34(6):243-254. [7]Huang Z,Chalabi Z S. Use of time-series analysis to model and forecast wind speed[J]. Journal of Wind Engineering & Industrial Aerodynamics,1995,56(2/3):311-322. [8]Erdem E,Shi J. ARMA based approaches for forecasting the tuple of wind speed and direction[J]. Applied Energy,2011,88(4):1405-1414. [9]Su Z,Wang J,Lu H,et al. A new hybrid model optimized by an intelligent optimization algorithm for wind speed forecasting[J]. Energy Conversion and Management,2014,85(9):443-452. [10]Lydia M,Suresh Kumar S,Immanuel Selvakumar A,et al. Linear and non-linear autoregressive models for short-term wind speed forecasting[J]. Energy Conversion and Management,2016,112(6):115-124. [11]Liu H,Tian H Q,Li Y F. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction[J]. Applied Energy,2012,98(1):415-424. [12]Liu H,Chen C,Tian H Q,et al. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks[J]. Renewable Energy,2012,48(6):545-556. [13]师洪涛,杨静玲,丁茂生,等. 基于小波-BP神经网络的短期风电功率预测方法[J]. 电力系统自动化,2011,35(16):44-48. [14]刘 莉,叶 文. 基于BP神经网络时间序列预测模型的降水量预测[J]. 水资源与水工程学报,2010,21(5):156-159 [15]Meng A B,Ge J F,Yin H et al.Wind speed forecasting based on wavelet packet decomposition and artificial neural networks trained by crisscross optimization algorithm[J]. Energy Conversion and Management,2016,114(6):75-88. [16]Haque A U,andal P M,Meng J,et al.Wind speed forecast model for wind farm based on a hybrid machine learning algorithm[J]. International Journal of Sustainable Energy,2015,34(1):38-51. [17]Hassen B. Multiple architecture system for wind speed prediction[J]. Applied Energy,2011,88(7):2463-2471. [18]Erasmo C.Wind speed forecasting in three different regions of Mexico,using a hybrid ARIMA-ANN model[J]. Renewable Energy,2010,35(12):2732-2738 [19]HO S L,Xie M,Goh T N,et al. A comparative study of neural network and Box-Jenkins ARIMA modeling in time series prediction[J]. Compute & Industrial Engineering,2002,42(2/3/4):371-375. [20]Li G Q,Xu S W,Li Z M. Short-term price forecasting for agro-products using artificial neural networks[J]. Agriculture and Agricultural Science Procedia,2010,1(156):278-287. [21]Yang H X,Zhao C,Du X J,et al. Risk prediction of city distribution engineering based on BP[J]. Systems Engineering Procedia,2012,5(3):55-60. [22]Wang Z,Wang F,Su S. Solar irradiance short-term prediction model based on BP neural network[J]. Energy Procedia,2011,12(39):488-494. [23]Zhang Y X,Gao X D,Katayama S. Weld appearance prediction with BP neural network improved by genetic algorithm during disk laser welding[J]. Journal of Manufacturing Systems,2015,34(11):53-59. [24]Zhen J X. Application of PSO-trained artificial neural network in high speed milling force modeling[J]. Comput Integrated Manufacturing Systems,2008,14(9):1709-1716. [25]胡寿松,张正道. 基于神经网络的非线性时间序列故障预报[J]. 自动化学报,2007,33(7):744-748. [26]杨 娜. 利用BP神经网络由特征气象要素预测土壤湿度[J]. 土壤通报,2011,42(6):1324-1329. [27]Chang Q L,Zhou H Q,Hou C J. Using particle swarm optimization algorithm in an artificial neural network to forecast the strength of paste filling material[J]. Internation Journal of Mining Scicence and Technology,2008,18(4):551-555. [28]Liang G M,Zheng X. An improved BP Neural Network based on IPSO and its application[J]. Journal Computes,2013,8(5):1267-1272.2.3 利用BP网络进行时间序列预测
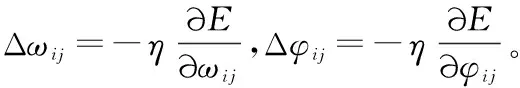
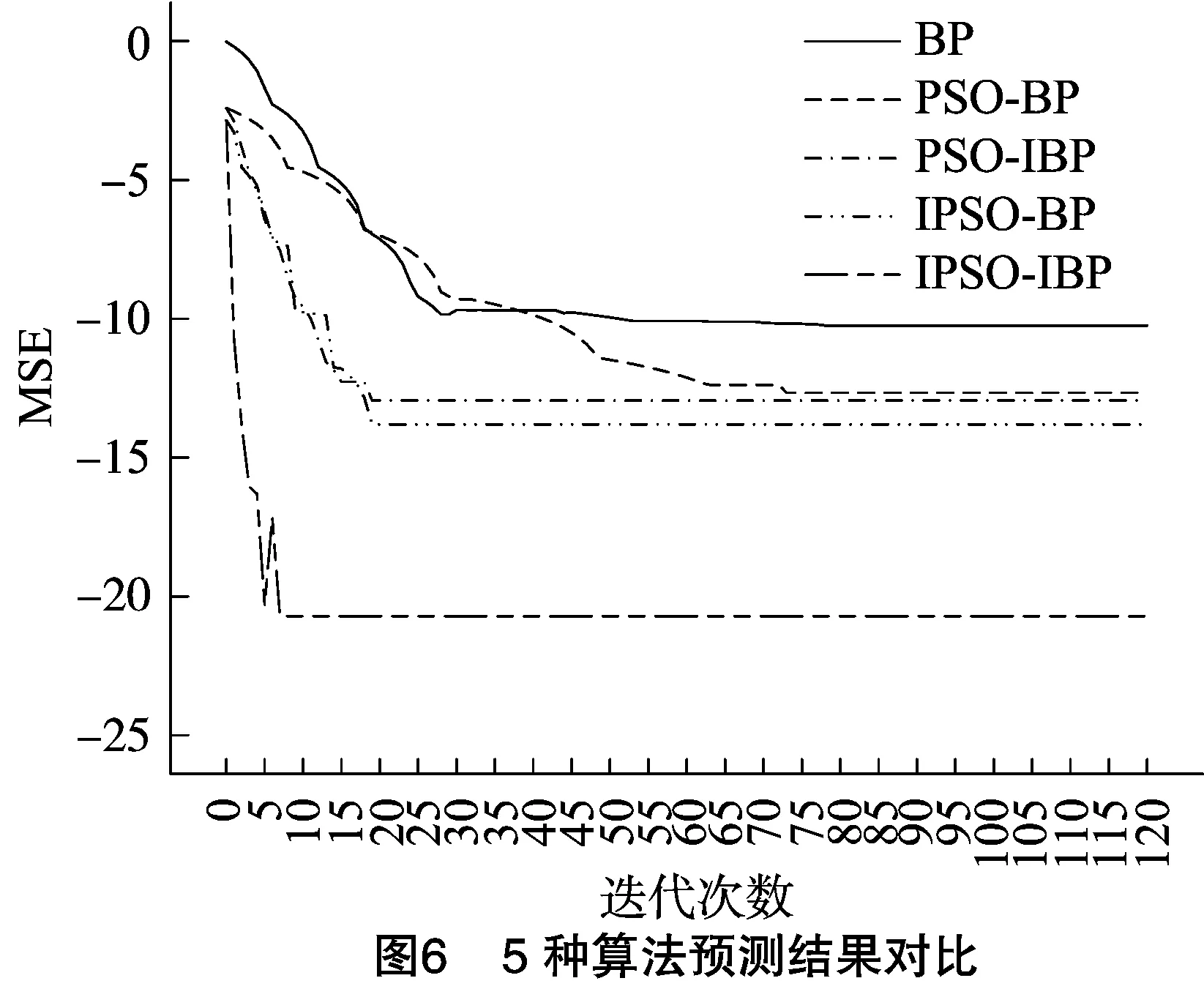
3 试验结果及讨论


4 结论
