红枣收获机骑跨式机架的优化设计
2018-06-07李琳琳王丽红李成松
李琳琳, 王丽红, 坎 杂, 付 威, 李成松
(石河子大学机械电气工程学院,新疆石河子 832000)
矮化密植红枣收获机作业环境复杂,机身振动较大。骑跨式机架作为红枣收获机的主要承载部件,支撑车身平衡,其稳定性、可靠性是机架设计时应考虑的重要因素。机架的结构及质量影响其固有频率,作业时,一旦激励频率与机架的固有频率耦合,机架将产生共振,影响红枣收获机的稳定性、可靠性。为了提高红枣收获机的稳定性、行驶安全性,降低收获机的振动,应对不满足要求的机架结构进行优化设计。目前国内外学者对机架优化设计方法已展开相关研究。韩红阳等在满足喷雾机机架刚度和强度的前提下,通过对机架采用轻量化设计,提高了机架的可靠性[1-2]。姚艳春等研究玉米收获机车架壁厚、刚度与固有频率的关系,以提高车架1阶固有频率为优化目标,对车架进行优化,明显改善了车架的振动特性[3]。本研究对红枣收获机骑跨式机架进行静力学分析和模态分析,根据分析结果对机架各构件厚度进行曲面响应设计,结合ANSYS软件计算各设计点对应的响应变量,并进行曲面响应分析,得到机架构件厚度的最优参数组合。将最优化机架的模态分析结果与外界激振频率进行对比分析,验证减振效果。
1 有限元模型的建立及静力学分析
1.1 机架模型的建立
红枣收获机骑跨式机架主要由方管、矩形管及角钢焊接而成,其材料为Q235,弹性模量为210 GPa,密度为 7 850 kg/m3,泊松比为0.3,方管、矩形管尺寸规格通常为 80 mm×100 mm×(6~8) mm、100 mm×100 mm×(6~8) mm,角钢的尺寸规格通常为180 mm×180 mm×10 mm。将在Solidworks软件中建立的三维模型导入Ansys分析软件,进行网格划分,设置单元尺寸为15 mm,划分后得到的单元总数为 123 801个,节点总数为522 758个,图1是机架的有限元模型。
1.2 静力学分析
红枣收获机受力比较复杂,用一般力学方法进行分析很难作出较精确的判断,因此应对机架进行静力学分析。红枣收获机骑跨式机架为承载式机架,载荷主要包括机架、发动机总成、驾驶室、液压油箱总成等质量。如图2所示,由于骑跨式机架左右对称分布,图2仅对右侧机架进行标注。机架上的各部分总成简化为集中力直接作用在相应的支撑位置,而机架自身质量按照均布载荷处理,并将收获机的四轮支撑与纵梁的交叉处设置为固定约束[4-5]。主要的静载荷及施加方式如表1所示。
求解后机架所得应力云图和变形云图如图3、图4所示,通过分析可知,最大应力出现在管与管的连接处,为 73.282 MPa;最大变形发生在发动机的安装位置,为 0.864 mm。机架材料的屈服极限σs为235 MPa,在安全系数n为1.5的情况下,满足强度设计要求。为提高机架的刚度和红枣收获机的工作稳定性,满足机架强度和刚度的前提下,对机架各构件的厚度进行轻量化设计。
2 机架的模态分析
由于红枣收获机在作业过程中不仅受到各零部件对机架施加的静载荷,也受到发动机、输送链等部件及地面等处的激振载荷,当机架的固有频率在激振频率范围内时,机架会产生共振,因此应对优化后的机架进行模态分析。由模态分析结果及与外界激振频率对比分析(表2)可知,机架的固有频率均在外界激振频率范围之内,易产生共振,因此应对机架进行优化设计。
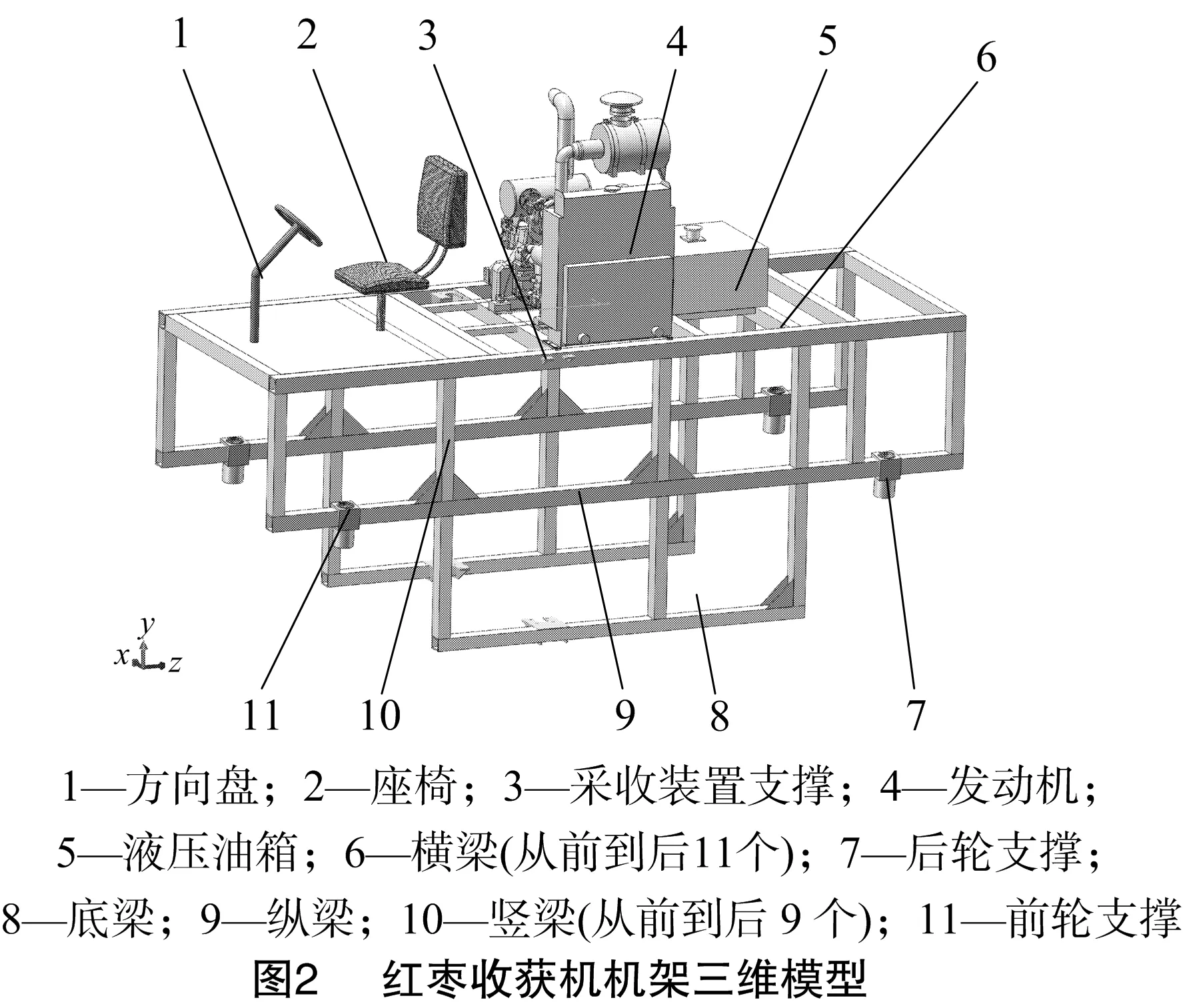

表1 有限元分析中各载荷及施加方式
注:发动机总成质量包括发动机净质量和装满冷却水的质量,液压油箱总成质量指装满油的质量。
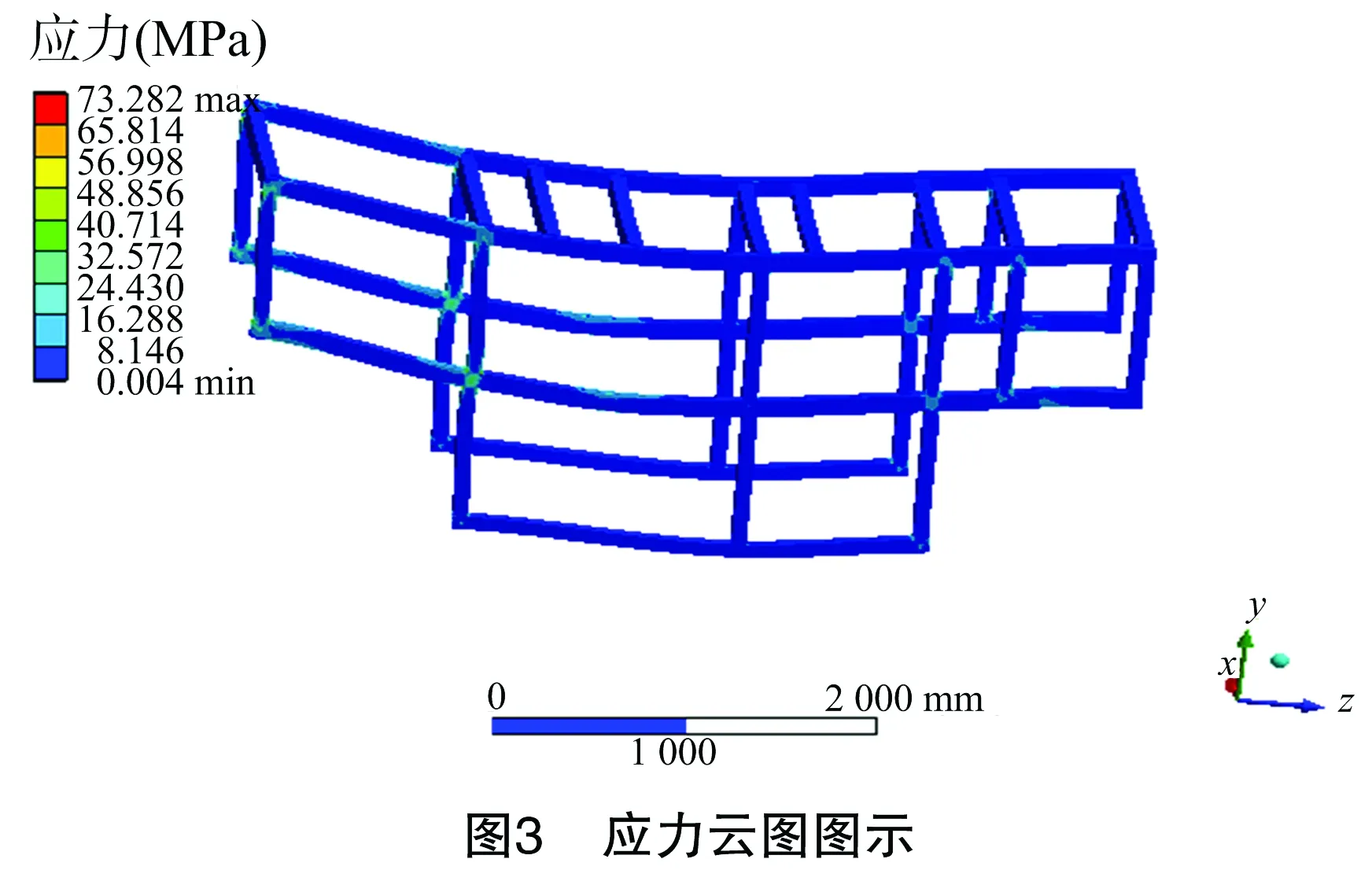


表2 模态分析结果对比
注:与外界激振频率对比分析表明,机架的固有频率均在采收装置、输送装置、发动机等关键部件以及地面对机架产生的激励频率范围之内。
3 机架优化设计
根据以上分析可知,机架的固有频率均未偏离激励频率范围,为避免红枣收获机在作业过程中发生共振,应对骑跨式机架进行优化设计。
3.1 机架结构优化数学模型
根据机架的静力学分析结果,将骑跨式机架的最大变形量设置为优化目标,而减小最大变形量往往会导致整个机架的质量增加,因此将机架的质量设置为另一个优化目标。各构件的厚度作为设计变量,在机架三维建模中定义4个设计变量:横梁厚度z1、竖梁厚度z2、纵梁厚度z3、底梁厚度z4,上限为8 mm,下限为6 mm,初始值均设为8 mm。优化设计的目的是为了获得机架各构件厚度的最优参数组合,尽量减小机架质量、提高力学性能。骑跨式机架构件厚度优化设计的数学模型为
设计变量
Z=[z1,z2,z3,z4]。
约束条件
6 mm≤zi≤8 mm,i=1,2,3,4。
目标函数:
fm(Z)min=f(z1,z2,z3,z4);
(1)
fδ(Z)min=f(z1,z2,z3,z4)。
(2)
3.2 机架结构优化数学模型响应曲面试验设计
采用Box-Behnken方法,以横梁厚度、竖梁厚度、纵梁厚度、底梁厚度4个因子为自变量,并取其范围为6~8 mm,按照方程xi(zi-zi0)/Δi对自变量进行编码。式中:zi为自变量的真实值;xi为自变量的编码值;zi0为试验中心点处自变量的真实值;Δi为自变量的变化步长;试验自变量因素编码见表3。
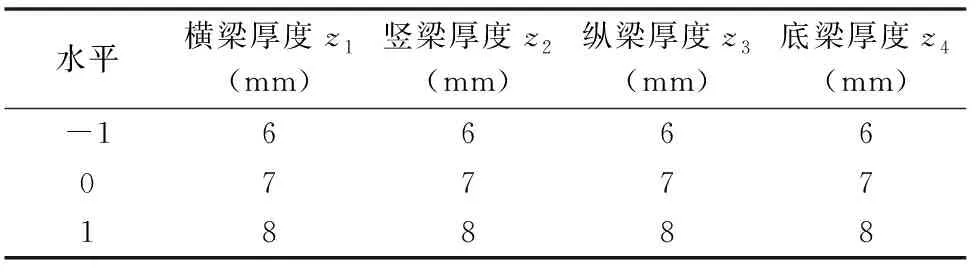
表3 机架结构优化数学模型的因素水平编码
利用统计学软件design-expert进行试验设计,得出24组最优化设计点,结合ANSYS软件对24组试验方案进行计算,试验设计及结果见表4。
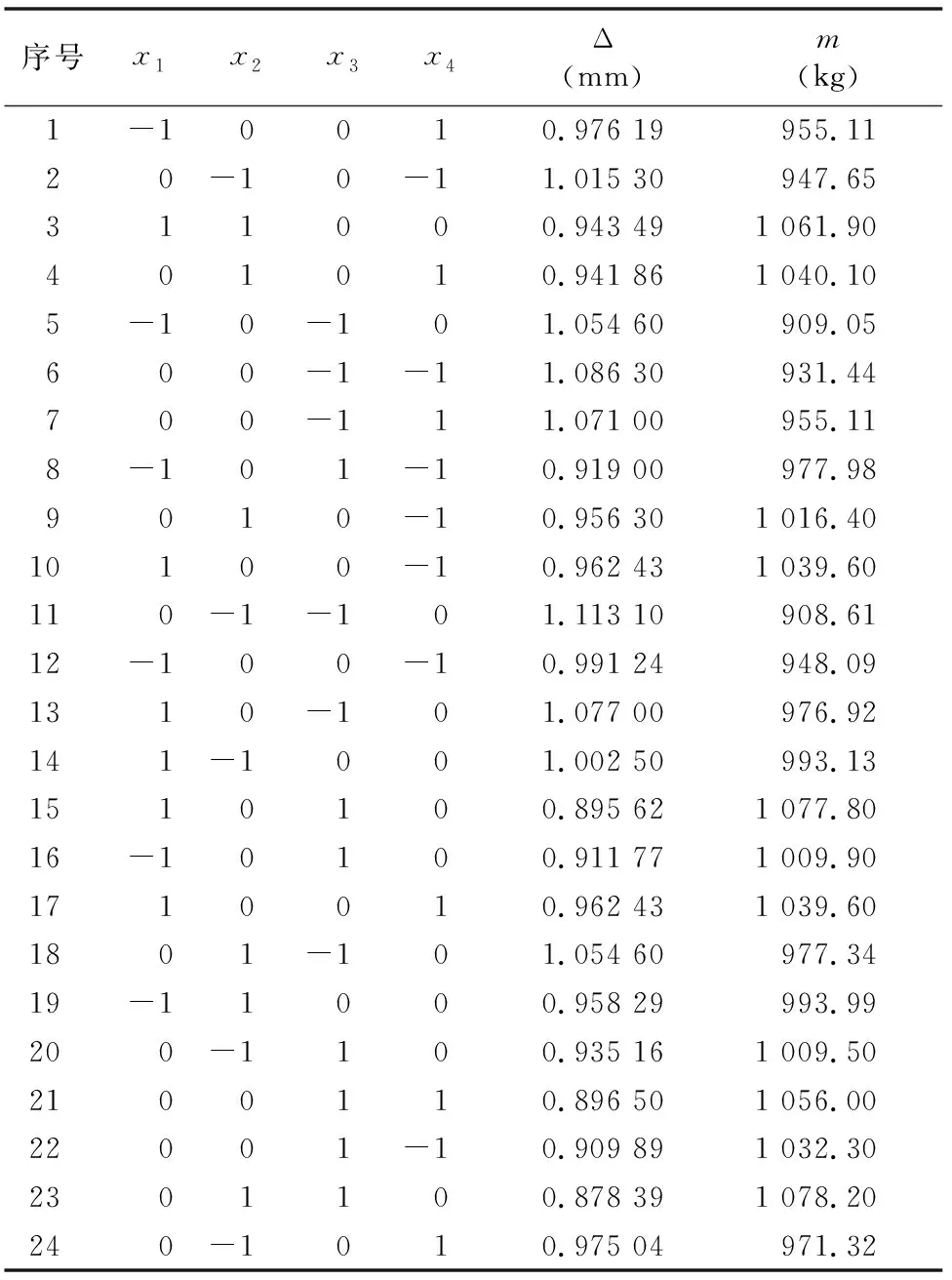
表4 机架结构优化数学模型的响应曲面设计与试验结果
注:Δ为机架的最大变形量;m为机架的质量。表6同。
3.3 机架结构优化数学模型的试验设计结果分析
3.3.1 回归方程及显著性检验 以机架的最大变形量为响应变量,对各因素进行二次多项式拟合,由于机架每个构件质量的降低都会对机架的质量有明显影响,因此仅针对机架的最大变形量进行二次回归模型系数显著性[6-7]分析,回归方程系数及显著性检验结果见表5。分析得到的编码回归方程为
fδ(x)=0.990 0-0.004 1x1-0.026 0x2-0.086 0x3-0.008 2x4-0.004 3x1x2-0.009 6x1x3+0.003 8x1x4+0.000 4x2x3+0.006 5x2x4+0.000 5x3x4-0.009 9x12-0.005 1x22+0.008 7x32-0.008 8x42。
将各因素编码公式代入编码回归方程,可得回归方程为
fδ(z)=0.980 6+0.205 5z1+0.027 2z2-0.146 0z3+0.039 6z4-0.004 3z1z2-0.009 6z1z3+0.003 8z1z4+0.000 4z2z3+0.006 5z2z4+0.000 5z3z4-0.009 9z12-0.005 1z22+0.008 7z32-0.008 8z42
利用模型的决定系数(回归平方和与总离差平方和的比值)R2来衡量回归方程的拟合程度,从分析中得到该R2为 0.991 6,接近于1,表明回归方程的拟合效果好。利用回归方程的整体显著性水平P来检验方程的显著性,由表5可知模型对应的P<0.000 1,说明该模型极显著。从表5可知,模型中x2、x3(P<0.000 1)均达到极显著,x4中度显著(0.01
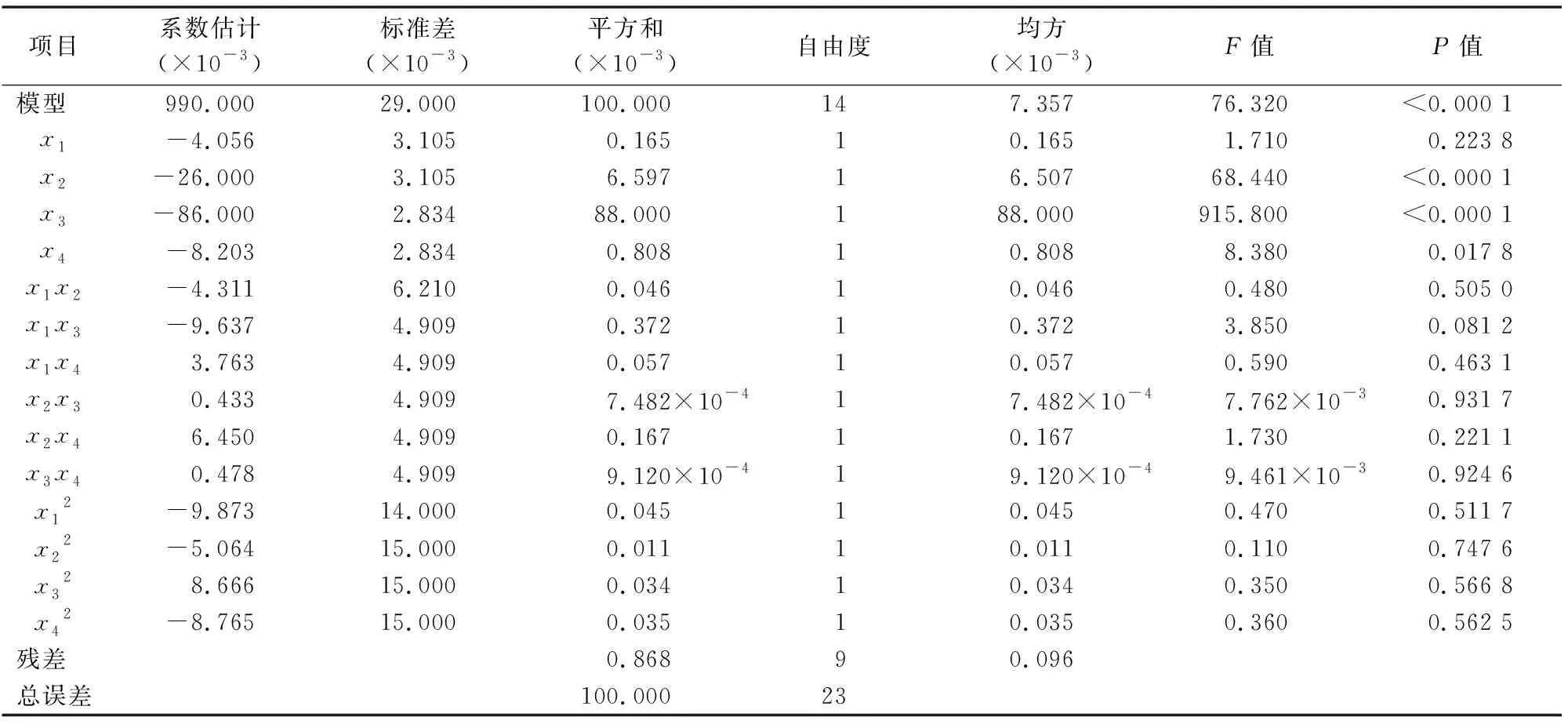
表5 回归方程系数及显著性检验
通过残差分析证实机架变形量模型正态性假定的真实性,根据分析得出残差的正态概率分布图。由图5可知,残差分布在-3~3之间,其正态概率分布大致在一条直线上,符合正态分布且不存在异常值会对回归估计结果产生影响。
模型预测值与试验值的关系如图6所示,结合回归方程系数及显著性检验(表5)可知,机架变形量的二次多项式回归模型拟合良好。
3.3.2 曲面响应优化分析 通过design-expert软件中的Optimization最优化分析得到35组二次多项式模型的最优化设计点,前10组最优化设计点如表6所示。根据表6中有利指标栏可知,第1组最优设计点的有利指标为0.989。由x1与x2的等值线(图7)可知,当x1为6 mm、x2为7 mm时, 综合指标最大,为0.989。
3.3.3 优化前后对比分析 根据表6最优化设计点建立机架的最优化模型,并对最优化模型进行静力学分析和模态分析,由此可知,优化后机架的质量为977.981 kg,减小11.17%,最大变形量为0.919 000 mm,增加0.055 mm,机架变形量变化可忽略不计。为验证减振效果,在模态分析的基础上对最优化模型进行谐响应分析[8-10]。
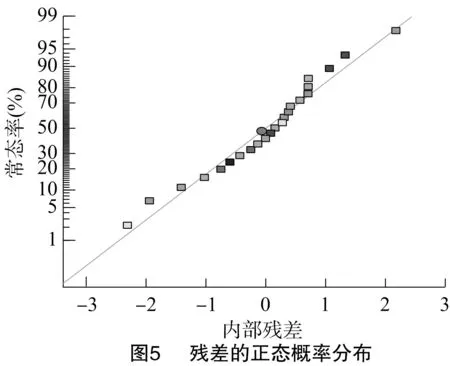
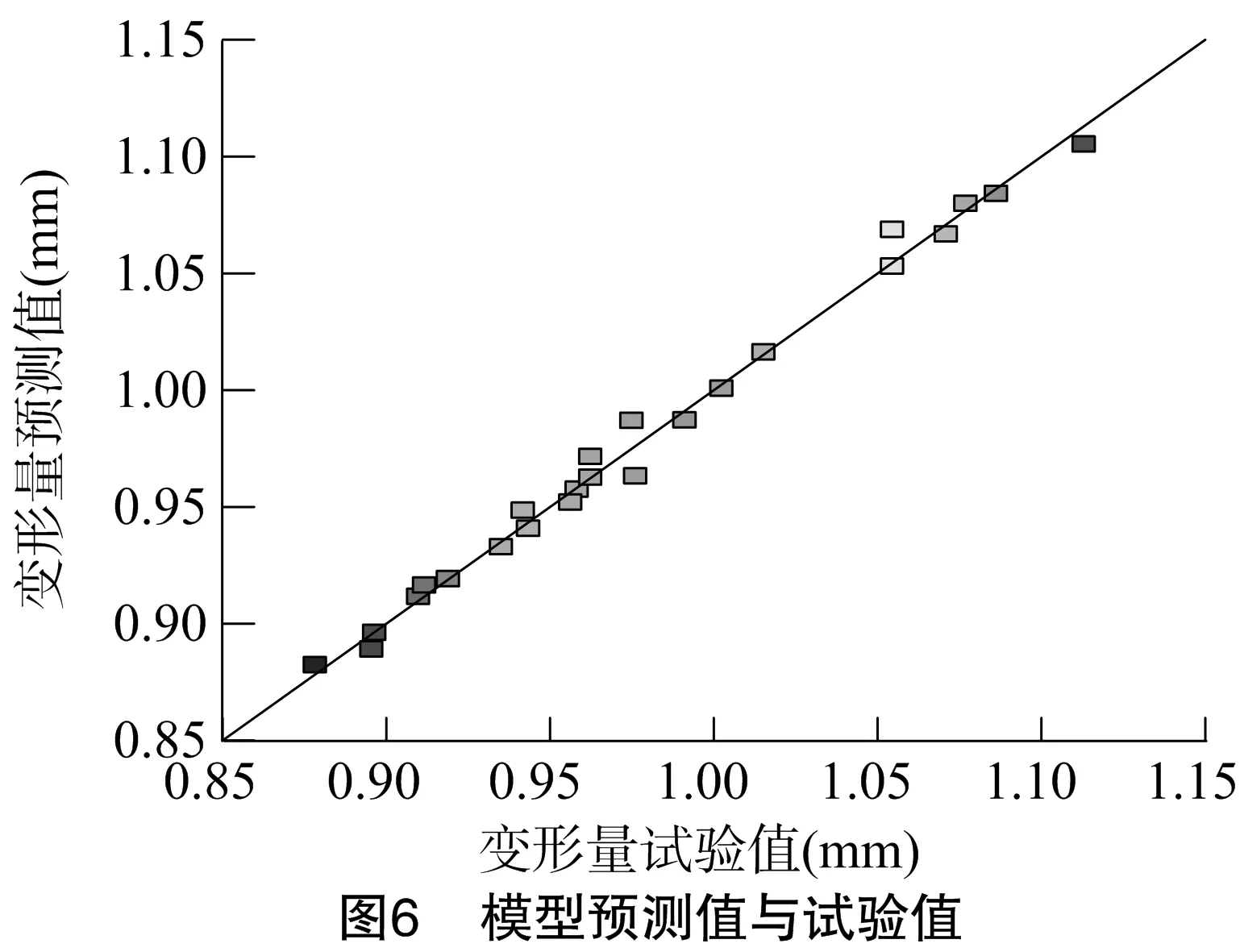
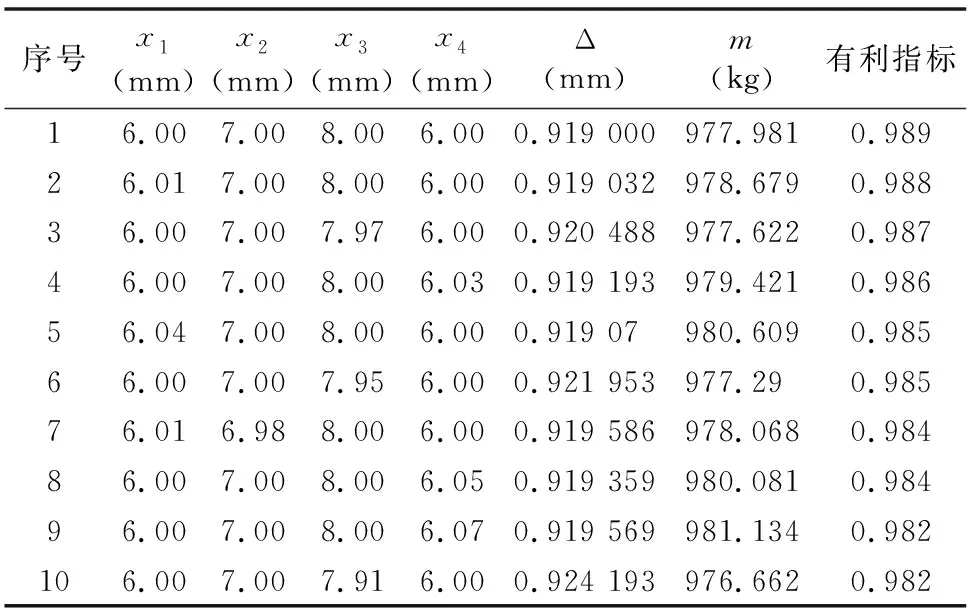
表6 最优设计方案

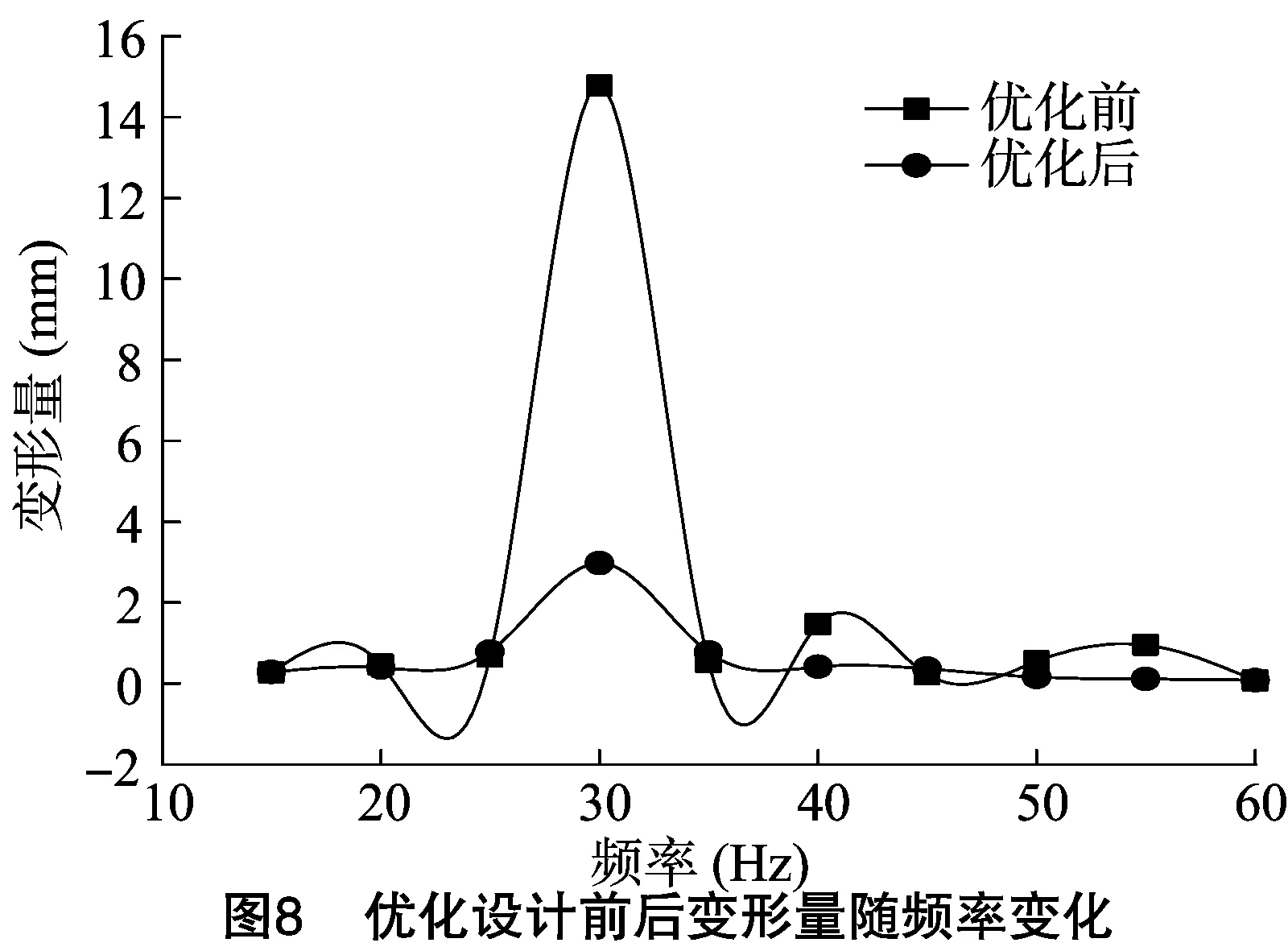
3.3.4 减振方案的谐响应分析 对最优化模型进行模态分析,并与外界激励进行对比分析可知,机架的固有频率未偏离发动机的激振频率范围,因此应对机架进行谐响应分析验证减振效果。在发动机的安装位置处施加最大激振载荷,垂直最大激励载荷设置为3 425 N,频率范围设置为15~60 Hz,分别对优化前、后的机架进行谐响应分析,分析结果如图8所示。由此可以看出,当频率为30 Hz时,机架的最大变形量由14.773 mm 降到2.977 mm,降低79.848%,起到明显的减振效果。
4 结论
建立机架有限元模型并进行静力学分析和模态分析,根据分析结果对机架各构件厚度进行响应曲面设计,结合ANSYS软件计算各设计方案的响应变量,利用design-expert软件中的模块进行分析和优化设计,获得机架各构件厚度的最优参数组合。响应曲面设计分析结果表明,机架的质量减小11.17%,机架的最大变形量为0.919 mm,满足设计要求。
对最优化模型进行模态分析,可知机架固有频率未偏离发动机激振频率范围,应对机架进行谐响应分析验证减振效果。结果表明,在30 Hz时最大变形量由14.773 mm减小到2.977 mm,降低79.848%,机架的振动特性得到明显改善。
参考文献:
[1]韩红阳,陈树人,邵景世,等. 机动式喷杆喷雾机机架的轻量化设计[J]. 农业工程学报,2013,29(3):47-53.
[2]陈树人,韩红阳,陈 刚,等. 喷杆喷雾机动态特性分析与减振设计[J]. 农业机械学报,2013,44(4):50-53.
[3]姚艳春,杜岳峰,朱忠祥,等. 基于模态的玉米收获机机架振动特性分析与优化[J]. 农业工程学报,2015,31(19):46-53.
[4]Ma Z D,Perkins N C. A track-wheel-terrain interaction model for dynamic simulation of tracked vehicles[J]. Vehicle System Dynamics,2002,37(6):401-421.
[5]曾 攀. 有限元分析及应用[M]. 北京:清华大学出版社,2008.
[6]任露泉. 回归设计及其优化[M]. 北京:科学出版社,2009.
[7]刘春景,唐敦兵,何 华,等. 基于响应曲面车削加工表面粗糙度稳健性分析[J]. 南京航空航天大学学报,2012,44(4):520-525.
[8]陈黎卿,李 艳,曹成茂. 基于遗传算法的山区微型播种施肥机减振优化设计[J]. 农业工程学报,2015,31(3):17-22.
[9]徐中明,余 烽,张志飞,等. 小型机动平台车体动态特性分析与减振设计[J]. 机械设计,2011,28(3):84-87.
[10]魏 凯. 基于虚拟分析的摩托车整车振动预测及减振研究[D]. 天津:天津大学,2007.
