LEO星座定轨的星间/星地观测方案优化
2018-06-06高华宇郭肃丽
高华宇,杜 兰,郭肃丽,于 晴
(1.中国电子科技集团公司 第五十四研究所,石家庄 050081;2.中国电子科技集团公司航天信息应用技术重点实验室,石家庄 050081;3.信息工程大学 导航与空天目标工程学院,郑州 450000)
0 引言
目前,近地轨道(low Earth orbit,LEO)全球星座主要应用倡导方向是“太空互联网”[1]。与导航星座相比,低轨卫星的优势是大大减少了卫星与地表的距离,使得数据传输更快,传输信号更强。已经有OneWeb、波音等公司纷纷寻求建立近地轨道卫星宽带网络,美国OneWeb公司提出的“星座互联网”计划首获美国官方批准,其目标是构建一个覆盖全球的高速宽带网络[2-3]。
LEO星座也可以参照全球卫星导航系统(global navigation satellite system,GNSS)星座自主定轨模式实现其自身的轨道确定。传统导航星座的正常运行主要靠地面站来维持,地面测控网布站受限。在LEO星座中采用星间链路技术[4],通过星间/星地链路联合定轨,仅需少量境内地面站的支持就可以实现星座的长时间自主定轨,弥补地面测控网布站的局限性[5-7]。
针对LEO星座,合理的星间/星地链路设计及观测方案设计可以有效提高卫星的定轨精度。本文参照铱星(Iridium)系统设计6/8近极轨LEO星座,建立星间链路,统计地面锚固站对LEO卫星的可视弧长,并仿真分析星地链路中地面锚固站和被观测目标卫星的选取,分析星间/星地链路的随机误差、系统误差对定轨精度的影响,以期给出合理的观测方案及建议。
1 LEO星座构型
1.1 Iridium系统
Iridium系统采用同构星座进行设计,整个星座由72颗卫星组成,其中6颗为备用卫星;星座分为6个轨道面,每个轨道面12颗卫星;轨道倾角86.4°,轨道高度780 km,轨道周期约为100 min[8-10]。
铱星系统最大的优势是实现全球覆盖,并实现对高纬度地区的多重覆盖;不足之处是对低纬度地区只能实现单重覆盖。
1.2 6/8极轨LEO星座
为了使用较少的LEO卫星实现全球覆盖,参考铱星系统,设计了由48颗LEO卫星组成的圆极轨星座,星座分为6个轨道面,每个轨道面放置8颗卫星,轨道倾角为84.6°,轨道高度为1 080 km。图1是LEO星座的二维覆盖图。从图1上可以看出:LEO星座可以实现全球覆盖,对高纬地区实现多重覆盖。
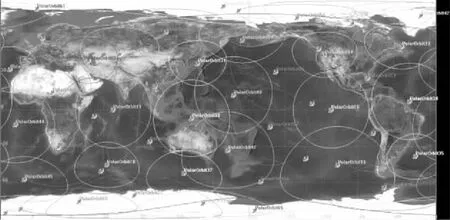
图1 LEO星座二维覆盖
2 星地/星间链路设计
星座链路设计包括星间链路设计和星地链路设计。星间链路主要由同一轨道面内的卫星之间以及相邻轨道面之间的链路组成,在同一轨道面内,每颗卫星与相邻的前后2颗卫星建立链路;相邻轨道面之间,每颗卫星只与距离最近的卫星建立链路,为了方便起见,链路连接按照图2的方式确定,实线连接表示建立星间链路;由于第1和第6轨道面互为逆行轨道,星间相对运动速度太快,因此不建立星间链路。
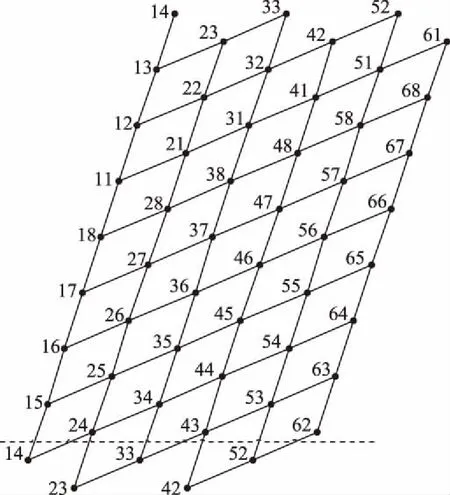
图2 星间链路设计
星地链路是由地面锚固站与卫星建立星地链路,采用双程测距观测量。本次设计的备选地面锚固站分别位于佳木斯、渭南、厦门。星地链路采用2种方式进行观测:1)地面锚固站对部分特定卫星进行全天弧段观测;2)地面锚固站在特定观测弧段内,对所有可视卫星进行即测。
3 星地/星间链路观测方程
3.1 星地观测链路
星地链路采用双程测距模式,测站发射无线电测距信号,由卫星转发,最后由原跟踪站接收。由于发射设备和接收设备使用同一个钟,因此测距值中不包含站钟和星钟的误差,跟踪站之间不需要严格的时间同步[10],无需考虑钟差对测量带来的误差。双程测距模型[11-12]为
ρcc=Rup+Rdown+cτdelay+2ΔDtrop+2ΔDion+
2ΔDrel+2ΔDant+2ΔDtide+ε
(1)
式中:ρcc为星地双程测距观测量;Rup为上行星地几何距离;Rdown为下行星地几何距离;c为光速;τdelay为设备时延;ΔDtrop和ΔDion分别为对流层和电离层延迟;ΔDrel为广义相对论改正;ΔDant为卫星和测站天线相位中心偏差;ΔDtide为地球潮汐改正;ε为随机误差。式(1)中的设备时延,电离层、对流层延迟,广义相对论改正,天线相位中心偏差,地球潮汐改正属于系统误差。令系统误差δ1为
δ1=cτdelay+2ΔDtrop+2ΔDion+
2ΔDrel+2ΔDant+2ΔDtide
(2)
不考虑光行时误差,上行和下行的星地间几何距离相等,即Rup=Rdown,则式(1)可以表示为
ρcc=2Rup+δ1+ε
(3)
3.2 星间观测链路
现在导航卫星星间链路主要采用星间伪距测量方式,考虑星间时间同步误差时间测量伪距观测方程[11-14]为
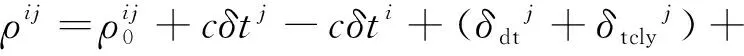
(4)

与星地链路处理方法相似,令系统误差δ2为
δ2=cδtj-cδti+(δdtj+δtclyj)+δion+
(δdri+δrclyi)+δrel+δmul
(5)
则式(4)可以表示为
(6)
4 实验与结果分析
文中定轨采用事后定轨方法,将一定观测弧段内的星间/星地观测数据传回地面站进行事后定轨,利用最小二乘方法进行参数估计,并给出观测弧段内的定轨精度[15]。
仿真弧段为2016-05-15的0时至2016-05-16的0时(1 d);采用前面提出的6/8近极轨LEO星座(共计48颗卫星),星间链路联通方式见图2;地面锚固站分别位于佳木斯、渭南、厦门,测站相对位置如图3所示。LEO卫星考虑的摄动力如表1所示,默认所有星间以及星地链路的系统误差设为2 m,随机误差为0.5 m。
LEO卫星编号规则:前1位代表轨道面编号,后3位代表该卫星在轨道面内的编号。例如:6001号卫星,6代表第6轨道面,001代表该轨道面内第1颗卫星。
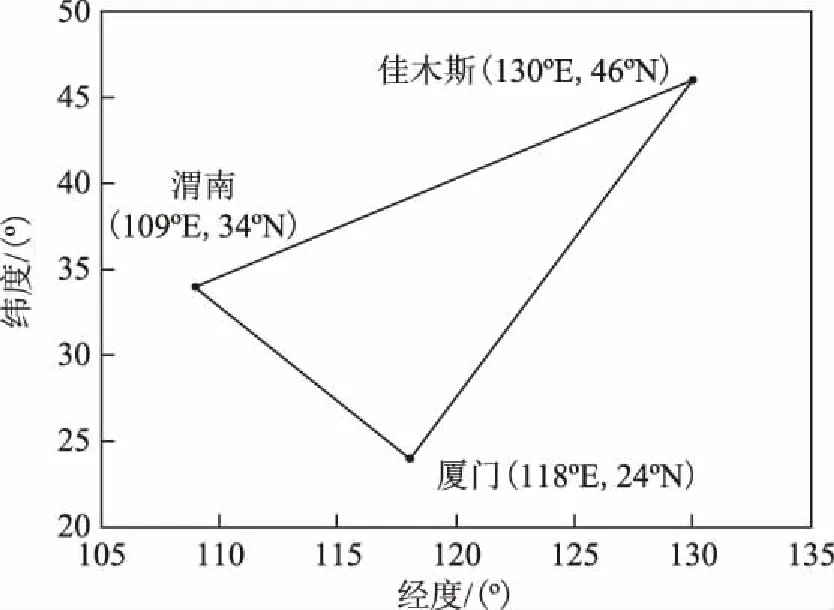
图3 地面锚固站位置
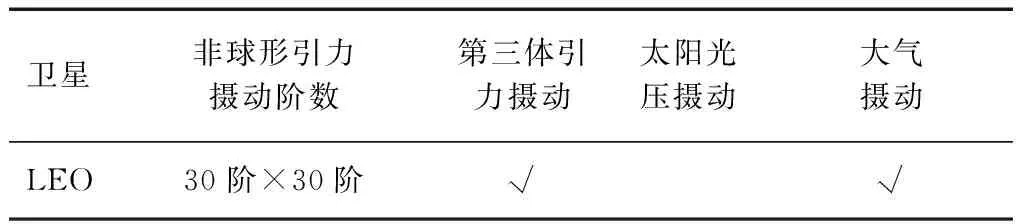
卫星非球形引力摄动阶数第三体引力摄动太阳光压摄动大气摄动LEO30阶×30阶√√
4.1 仿真实验流程及定轨精度
首先,按照LEO星座设计模拟真实轨道作为参考轨道;然后,根据观测方程计算星站距和星间距,并加入系统误差和随机误差作为观测数据;第三,使用星间/星地链路的观测数据进行定轨,确定轨道精度。
定轨精度评定方法:在每个历元时刻,分别比较解算出的轨道和参考轨道在径向(R)、切向(T)和法向(N)的位置、速度误差ΔXm,计算不同历元时刻的均方根误差(root mean square error,RMSE)作为定轨精度[8,16],RMSE值越小,定轨精度越高。RMSE的计算方法为
(7)
式中ΔXm为m时刻解算轨道相对参考轨道的R/T/N分量误差,m=1,2,…,N。
4.2 地面锚固站观测弧长统计
卫星定轨精度与观测的数据量和观测弧长有密切联系。相同的观测弧段,减少采样间隔可以增加观测数据量;地面锚固站所处的地理纬度是影响观测弧长的主要因素,选取了分别位于佳木斯、渭南、厦门的锚固站,使用STK(satellite tool kit)软件进行了仿真,定量分析了1 d内,3个锚固站对LEO星座中1颗卫星的观测弧长。
表2给出了3个地面锚固站对1001号卫星的可视弧长。图4给出了锚固站对1001号卫星可视弧段个数。
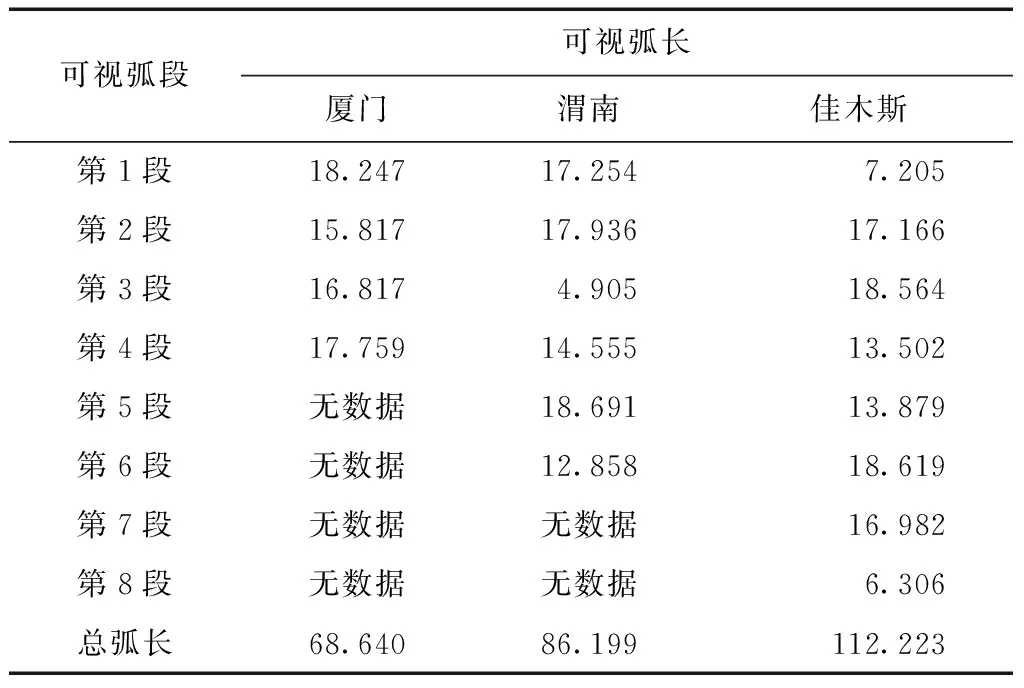
表2 锚固站对1001号卫星可视弧长 min

图4 锚固站对LEO卫星可视弧段个数
从表2、图4中可以看出:
1)1 d范围内,地面锚固站的纬度越高,对近极轨卫星的可视弧长越长。3个锚固站纬度由高到低依次为佳木斯站、渭南站、厦门站。其中,佳木斯站与卫星的可视弧长最长,为112 min;弧长最短的是厦门站,为68 min。
2)1 d范围内,高纬地区对近极轨卫星的可视弧段比低纬地区多。从图4中可以看出,佳木斯站对卫星的可视弧段为8个,渭南站为6个,厦门站为4个。
3)从观测弧长方面,高纬站佳木斯站对卫星的可视弧长最长,可视弧段最多;因此优先考虑佳木斯锚固站进行观测。
4.3 地面锚固站数量的选取
加入地面锚固站,分析星地观测量对卫星定轨精度的影响。地面锚固站分别位于佳木斯、渭南、厦门,为分析方便,暂定地面锚固站只观测6001号卫星。仿真分为以下4种方案进行,其中方案一为对比实验:
方案一:只有LEO星座及星间链路观测量(以下简称星间链路方案);
方案二:星间链路+1站观测数据;
方案三:星间链路+2站观测数据;
方案四:星间链路+3站观测数据。
表3给出了4种方案每个轨道面内8颗卫星的平均3维定轨精度。
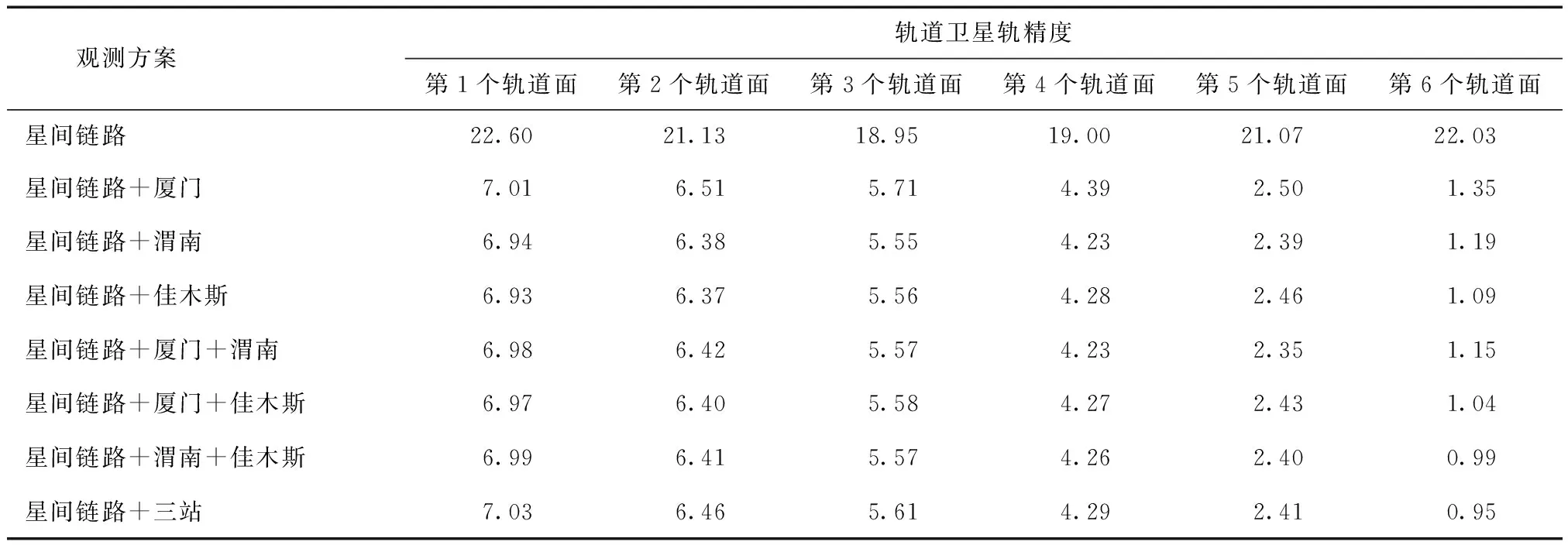
表3 地面锚固站的数量及地理位置影响下的定轨精度 m
从表中可以看出,在本次仿真条件下:1)加入星地观测量,卫星定轨精度从20 m量级提高到10 m以内;2)被观测卫星所在轨道面的卫星定轨精度最好,其他轨道面随着轨道面之间链路观测误差的累积,定轨精度依次变差,在本次仿真实验中,地面锚固站直接观测的第6个轨道面定轨精度最好,平均定轨精度达到1 m量级,随着轨道面之间链路误差的累积,第5个至第1个轨道面的卫星定轨精度依次变差;3)为保证定轨精度,同时兼顾星地观测弧长及节约地面站资源,建议选择佳木斯站进行观测。
从表3的结果可知,卫星定轨精度受测站数量及地理位置影响不大,只需一个测站即可;通过4.2节的分析可知,佳木斯站对卫星可视弧长最长,因此建议选择佳木斯站作为地面锚固站。
4.4 星地链路目标卫星选取及观测模式对比
佳木斯锚固站对LEO星座的观测可以采取2种方式:1)1 d范围内,佳木斯站对目标卫星进行全天跟踪;2)特定弧长内(如2 h),佳木斯站对所有可视卫星进行观测。
针对第1种观测模式,需要确定被观测的目标卫星。由于LEO星座为非对称星座,第6个轨道面与第1轨道面互为逆行的,相互之间没有建立星间链路;而第2个~第5个轨道面与前后轨道面都建立了星间链路,因此需要考虑目标卫星是否位于第1个、第6个轨道面。另外,为了节省地面站的资源,需要分析对同一轨道面内所有卫星进行观测和对一颗卫星进行观测是否能达到相同的定轨精度。本次仿真方案如下:
方案一:佳木斯站观测6001号卫星与观测第6个轨道面所有卫星,对比定轨精度;
方案二:佳木斯站观测2001号卫星与观测第2个轨道面所有卫星,对比定轨精度;
方案三:佳木斯站观测1001、2001、3001、4001、5001和6001号卫星,分析定轨精度;
方案四:采用第二种观测模式,佳木斯站在11时至13时对所有卫星进行观测,分析定轨精度。
表4给出了佳木斯站对不同观测目标进行观测的定轨结果,分别给出了每个轨道面内所有卫星的平均3维定轨精度。

表4 锚固站观测不同目标卫星时的定轨精度 m
从表中可以看出:
1)按照方案三进行观测,定轨精度最好。与其他方案相比,按照方案三进行观测各个轨道面定轨精度在3 m左右,精度最优;各个轨道面之间定轨精度没有较大差距。
2)被观测卫星所处的轨道面定轨精度最优。从方案一和方案二定轨结果看,无论被观测卫星是1颗还是多颗,被观测卫星所处轨道面的定轨精度最优,离该轨道面越远,定轨精度越差。
3)从方案四定轨结果看,不同轨道面之间定轨精度有一定差距。这与在特定观测弧段内地面站对卫星的覆盖率有关,有待后续研究。
4.5 系统误差和随机误差对定轨精度的影响
本次研究只给出了系统误差和随机误差的量级,为了分析系统误差和随机误差对定轨结果的影响,通过仿真实验进行分析。在上述2次仿真结果的基础上,系统误差设置0.5、1、2、3、4、5 m量级,随机误差设置0.5、1、1.5、2、2.5、3 m量级。
星地和星间链路的系统误差、随机误差有所区别;因此分别考虑星地、星间链路的影响,测试分为以下2种:
1)星地链路的系统误差为2 m,随机误差为0.5 m,保持不变,星间链路设置分为:方案一,设置随机误差为0.5 m,依次变化系统误差;方案二的系统误差设置为2 m,依次变化随机误差。
2)星间链路的系统误差为2 m,随机误差为0.5 m,保持不变,星地链路设置分为:方案一,设置随机误差为0.5 m,依次变化系统误差;方案二,系统误差设置为2 m,依次变化随机误差。
表5和表6给出了星间链路和星地链路的系统误差、随机误差对定轨精度的影响。
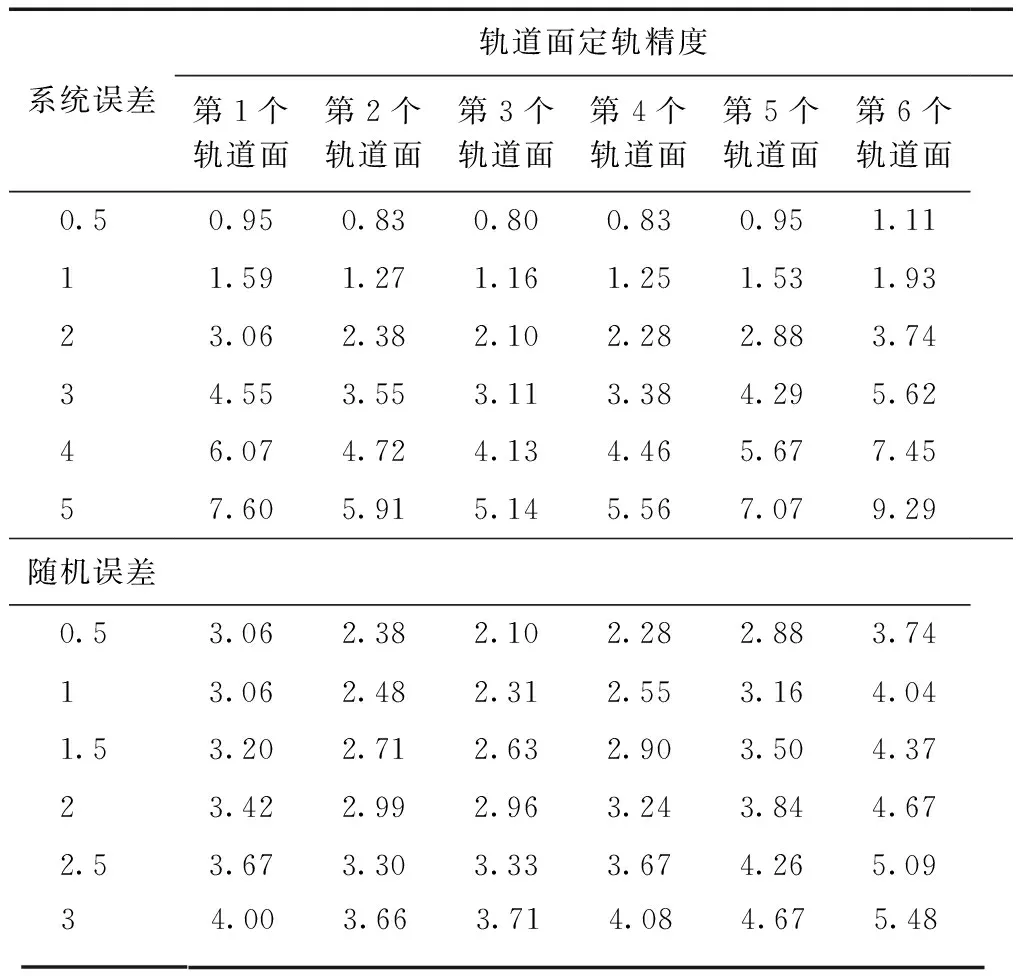
表5 星间链路系统误差、随机误差影响下的定轨精度 m
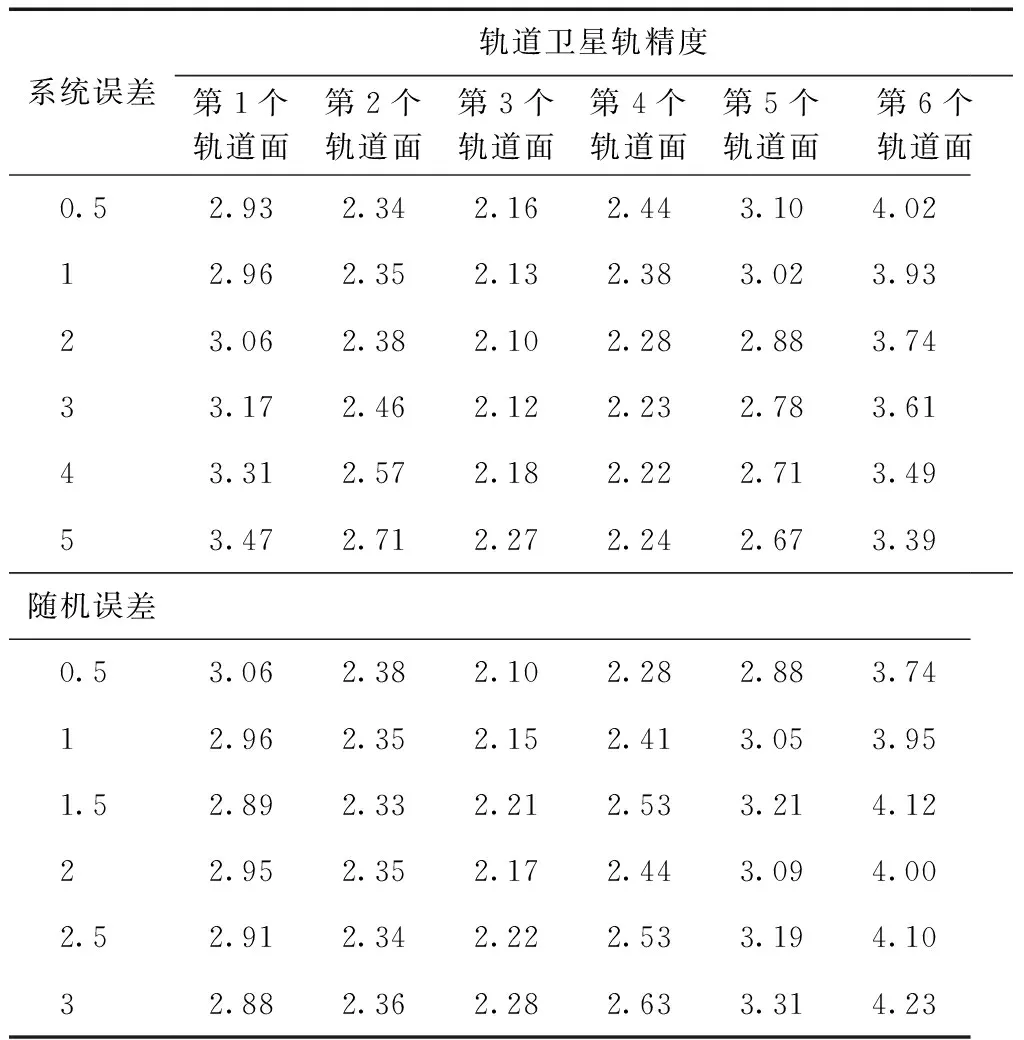
表6 星地链路系统误差、随机误差影响下的定轨精度 m
从表中可以看出,在本次仿真条件下:
1)从系统误差结果看,卫星定轨精度对星间系统误差的变化很敏感,而对星地系统误差的变化不敏感。星间链路系统误差每增加1 m,卫星定轨精度变差1~2 m;星地链路系统误差每增加1 m,卫星定轨精度变化0~0.2 m。
2)从随机误差结果看,卫星定轨精度对星间链路随机误差的变化较星地链路更敏感。星间链路随机误差每增加1 m,定轨精度变差0~0.8 m;星地链路随机误差每增加1 m,定轨精度变化0~0.4 m。
5 结束语
针对本文阐述的6/8低轨卫星星座观测方案优化问题,利用最小二乘法进行事后批处理定轨,通过仿真实验分析了地面站、目标卫星选取以及星间/星地链路系统误差、随机误差对定轨精度的影响,同时通过STK软件对地面锚固站对卫星的可视弧长进行了统计。通过对仿真结果进行分析,得出以下结论:
1)星地链路地面锚固站选择条件:地面锚固站的加入能够将LEO卫星定轨精度由20 m量级提升至10 m以内,但是只需在3个锚固站中选择1个即可,无需多个。
2)星地链路选星条件:建议被观测的目标卫星在每个轨道面中各选1个,这样各个轨道面之间的定轨精度相差较小,而且定轨精度最优。
3)卫星定轨精度对星间链路的系统误差很敏感,系统误差每增加1 m,卫星定轨精度变差1~2 m。而星地链路系统误差、随机误差的变化对定轨精度影响不大。因此,后续研究降低星间链路系统误差的方法很有意义。
[1] 陈忠贵,帅平,曲广吉.现代卫星导航系统技术特点与发展趋势分析[J].中国科学,2009,39(4):686-695.
[2] 杨力,郭飞霄,文援兰,等.单锚固站辅助导航星座自主定轨分析[J].飞行器测控学报,2013,32(5):444-448.
[3] 杨宁虎,陈力.卫星导航系统星间链路分析[J].全球定位系统,2007,32(2):17-20,32.
[4] 候颖,米志超,于卫波,等.星地一体化导航系统星间链路仿真及分析[J].通信技术,2014,47(2):145-149.
[5] 孟轶男,唐银银.导航星座星间链路仿真分析[J].宇航计测技术,2014,34(4):15-17,44.
[6] 罗大成,刘岩,刘延飞,等.星间链路技术的研究现状与发展趋势[J].电讯技术,2014,54(7):1016-1024.
[7] 陈艳玲,胡小工,周善石,等.基于星间测距的导航卫星自主定轨新算法[J].中国科学,2015,45(7):1-8.
[8] 张颖,王化民.基于GSM的铱星通信系统[J].航海技术,2013(3):35-37.
[9] 张洪波.航天器轨道力学理论与方法[M].北京:国防工业出版社,2015.
[10] 周建华,徐波.异构星座精密轨道确定与自主定轨的理论和方法[M].北京:科学出版社,2015.
[11] 张博.卫星导航系统星地/星间链路联合定轨方法研究[D].郑州:信息工程大学,2015.
[12] 朱俊.基于星间链路的导航卫星轨道确定及时间同步方法研究[D].长沙:国防科学技术大学,2011.
[13] 张艳,张育林.基于星间测量的异构星座自主导航方法研究[J].宇航学报,2005,26(增刊):30-34.
[14] 黄荣府.星间精密测距技术[D].南京:南京理工大学,2005.
[15] 刘伟平.导航卫星快速定轨和预报方法研究[D].郑州:信息工程大学,2011.
[16] 高华宇,耿虎军,杜兰,等.系统差及南纬站对GEO多站差距定轨精度的影响分析[J].无线电工程,2017,47(3):35-38.
