基于轨道动态模型的星间链路测距随机误差测试方法
2022-08-22胡帆尹卿李振东于澎方凯白力舸
胡帆 尹卿 李振东 于澎 方凯 白力舸
(北京空间飞行器总体设计部,北京 100094)
卫星作为星座内的节点,精确确定其在星座内的相对位置是维持稳定星座构型的基础,也是保障通信链路物理层稳定性和可靠性的基础。由于在轨工作条件下卫星之间通信距离较远,目标卫星在接收具有多普勒效应的星间测距信号时,往往在星上预设通信双方的轨道信息,并实时计算辅助捕获信息,以便尽量提升信号捕获锁定效率。相对运动中细微的时间检测偏差,将导致目标卫星在接收捕获信号时的测距误差大幅增加,因此,在轨道动态条件下卫星相对距离准确度(即测距随机误差)的精确测量是卫星测距功能地面测试的难点。
在实际测试过程中,被测卫星作为接收端需要测试设备模拟与之通信的其他目标卫星发射信号,通信信息及测距信息调制于发射信号上,被测卫星使用辅助捕获信息对接收到的测距信号进行解析,恢复测距信息。测试设备模拟的通信目标与被测卫星位置会相对变化,当前测试所涉及的位置变化场景主要有静态场景、线性动态模拟场景、三角波动态模拟场景、正弦波动态模拟场景等。上述场景针对单台设备的动态接收性能具备一定的模拟验证能力,但在整星状态下,卫星实际在轨运动时的轨迹会根据其他分系统提供的参数变化,静态场景等对卫星在轨实际工作性能进行预示仍存在一定的不确定性。因此,研究地面测距模拟理论值的准确度,是提高测距随机误差测试结果准确性的重要途径。
现有国内外测距随机误差测试主要集成于星间链路测试平台,用于对星间链路和星地链路的测距随机误差、测距一致性等指标进行验证。国外全球导航卫星系统(GNSS)星间链路测试平台的研究项目种类多,各有侧重。GNSS多星座模拟器(NAVYS)是针对GNSS的星座模拟设备,将包含独立的卫星轨道参数、卫星时钟、卫星天线方向图、功率参数、波形、伪随机码和多径传输方案等的完整配置端口提供给用户,能够对现有的星座及未来将会有的GNSS星座信号进行全方位仿真模拟[1]。伽利略卫星信号测试设备(GSVF)专用于卫星导航系统模拟测试,可对计划中的伽利略卫星导航信号和信息结构性能进行评估[2-5]。国内导航系统模拟平台侧重于其他卫星导航电文对被测卫星星历等的影响,能够将被测卫星的导航工作状态进行系统性的测试[6];卫星网络半实物仿真环境可对卫星网络进行建模,在网络层模拟卫星网络的拓扑结构、卫星轨道运行带来的动态拓扑变化,以及空间电磁信号传输导致的长时延、高误码率等空间环境特点,同时为网络管理提供虚拟的对象[7]。现有测试平台在进行动态测距随机误差功能测试时,采用的测试方法并未对轨道动态条件下地面距离模拟理论值的准确度进行深入分析。
本文提出基于轨道动态模型的星间链路测距随机误差测试方法,以提高对星间测距精度的测试能力。根据轨道六根数对轨道动态条件下的星间距离进行理论分析;针对运动中卫星的多普勒效应,提出轨道动态模型,模拟被测卫星以外卫星的星间链路距离动态信号,在被测卫星接收信号后进行测距计算;通过分析卫星地面测距模拟理论值的准确度影响,提出被测卫星的星间测距随机误差计算方法;将轨道动态星间测距随机误差测试方法应用于测试系统设计,进行工程验证。
1 星间距离理论分析
在轨道动态条件下计算被测卫星与通信目标卫星之间的相对位置关系时,可将卫星抽象为质点,在地心第一坐标系OXYZ中可以根据轨道六根数对t时刻卫星位置坐标(x,y,z)进行计算[8]。

(1)
式中:r为地心距;Ω为升交点赤经;u为纬度幅角;i为轨道倾角。
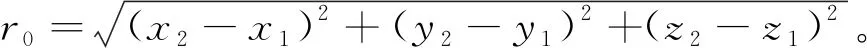
在地面测试过程中,采用地面测试设备模拟卫星发出经过距离延迟产生的星间链路距离动态信号。其原理为:在发射信号时根据仿真计算获得星间距离值进行相应的延迟,例如某时刻t,星间距离为d,则时刻t的星间链路信号延迟d/c再发射,其中,c为光速。
2 星间距离动态信号的地面模拟
设在测试时间段内{t1,t2,t3,…,tN}时刻仿真产生的星间距离分别为{d1,d2,d3,…,dN},星间链路信号生成模块产生的{t1,t2,t3,…,tN}时刻星间链路发射信号模拟星间距离的影响,由星间链路信号生成模块对其分别进行时间延迟后发出,最终星间链路发射信号调整为{t1+d1/c,t2+d2/c,t3+d3/c,…,tN+dN/c},使发出的星间链路信号携带轨道动态距离信息。星间链路接收机进行接收测距的时候,仍在默认的{t1,t2,t3,…,tN}时刻进行采样测距,获得的测距值即带有星间距离信息,并叠加有自身设备测距随机误差。其中,N为测试时间段内采样个数。
卫星在轨相对运动产生多普勒效应的同时,也伴随着星间绝对距离的变化,表现为星间信号传输时延的变化。星间链路距离动态信号发射设备组成如图1所示。其中,卫星轨道仿真计算模块根据输入的卫星轨道参数对星间距离进行实时仿真计算。

图1 星间链路距离动态信号发射设备组成


注:(t)为1级调制后通信支路;(t)为1级调制后测距支路;Δt为每间隔T0插入的时延。
3 星间测距随机误差计算方法
卫星进行星间测距时,会将实际发射时刻为{t1+d1/c,t2+d2/c,t3+d3/c,…,tN+dN/c}的信号默认为{t1,t2,t3,…,tN}时刻发射,因此进行接收采样测距后带有星间距离信息。设测距时刻为{t1′,t2′,t3′,…,tN′},测距值为{r1,r2,r3,…,rN},该测距值覆盖了卫星的在轨真实工况,变化范围较大,需要应用计算距离动态测距值的随机误差方法。
星间链路接收机测得的实时测距值及其组成部分可以表示为
r(t)=c(τs+τr)+L+d(t)+Δρ+v(t)
(2)
式中:r(t)为t时刻卫星轨道动态伪距测量结果,m;τs为星间测距测试设备发射通道时延,s;τr为卫星测距设备接收通道时延,s;L为测试电缆长度,m;d(t)为t时刻轨道动态条件实时仿真距离值,m;Δρ为地面测试设备和卫星之间的钟差;v(t)为星间链路接收机测距随机误差。
以上组成部分中,c,τs,τr,L均为常量,在同源测试的情况下,Δρ也为常量,均不影响测距随机误差的计算,所以仅需要对r(t)-d(t)取标准差估计,就可以得到v(t)的估计值。因此,可以将距离动态测距值{r1,r2,r3,…,rN}减去测距时刻星间链路距离动态信号发射设备仿真计算产生的对应时刻星间距离值,获得减后序列。设测距时刻{t1′,t2′,t3′,…,tN′}对应的仿真星间距离为{d1′,d2′,d3′,…,dN′},则减后序列为{r1-d1′,r2-d2′,r3-d3′,…,rN-dN′},该序列包含测距值观测数据残差,对该序列求标准差,即得到星间链路接收机的测距随机标准差估计为
(3)
式中:i=1,2,…,N。
4 测试方法验证
整个星间链路测距随机误差测试系统组成如图3所示。其中:卫星轨道仿真计算模块和星间链路信号生成模块组成前文所述星间链路距离动态信号发射设备,它与测距随机误差计算模块共同组成了地面测试设备,测距随机误差计算模块负责完成将实时测距值序列减去对应时刻的仿真实时距离值,并完成标准差计算,从而完成测距随机误差计算。需要说明的是,本文采用的是同源测距方法,即地面测试设备与被测卫星使用的是同一个时钟信号基准,即双方的秒脉冲和用于产生测距信号的时钟是完全同步的。如果采用非同源测试方法,则需要在图3中增加钟差测量设备,且式(2)中的实时测距值除了要减去仿真实时距离值,还要减去实时钟差。
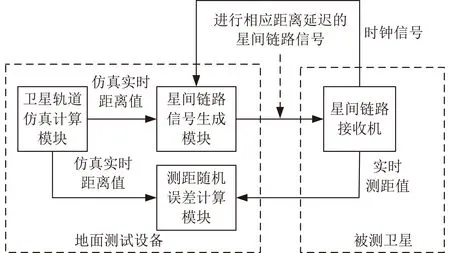
图3 星间链路测距随机误差测试系统组成
采用本文方法对某卫星的星间链路测距随机误差进行测试。此卫星的星间链路测距信号体制为:以0或者t0整倍数时刻处为起始时刻,每个t0为1个时隙,前t0/2发射、后t0/2接收,或者前t0/2接收、后t0/2发射,具体发射与接收顺序,由地面发送时隙表指令进行配置,本文以卫星的星间链路接收机在每个t0时隙的后t0/2进行采样测距为例进行描述,卫星的具体采样测距时刻为t0时隙的11/12t0处,对应的地面测试设备则在每个t0时隙的前t0/2发射测距星间链路信号,如图4所示。
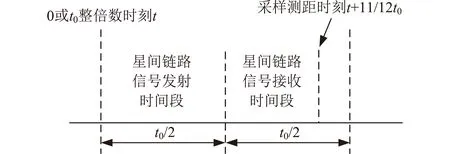
图4 星间链路信号发射与接收时间段示意
以起始时刻选为0时刻为例,则地面测试设备的星间链路距离动态信号的发射时刻{t1,t2,t3,…,tN}为{0,t0,2t0,…,tN},对应时刻仿真产生的星间距离分别为{d1,d2,d3,…,dN},最终对应{t1,t2,t3,…,tN}时刻的星间链路发射信号分别在{0+d1/c,t0+d2/c,2t0+d3/c,…,tN+dN/c}时刻发出。卫星在每个t0时隙的11/12t0处进行测距,所以测距时刻{t1′,t2′,t3′,…,tN′}实际为{11/12t0,(t0+11/12t0),(2t0+11/12t0),…,tN′},如图5所示。

图5 起始时刻为0时星间链路信号发射与接收时间段示意
在进行测距值随机误差计算时,被扣减的仿真测距值应选取{11/12t0,(t0+11/12t0),(2t0+11/12t0),…,tN′}时刻对应的实时仿真测距值。
在卫星研制过程中,采用本文方法对星间链路接收机测距随机误差进行测试,均取得了良好效果。地面测试设备仿真2颗卫星实时星间距离,并发射星间链路距离动态信号,星间链路接收机获得的实时测距值(以传输延迟时间代表距离值,星间距离等于传输延迟时间和光速的乘积,下同)见图6。地面测试设备仿真产生的模拟距离理论值见图7。实时测距值减去仿真实时距离值后,测距值曲线见图8。图9为实时测距值减去仿真实时距离值后的局部2 h图。

图6 星间链路接收机获得的实时测距值

图7 地面测试设备仿真产生的模拟距离理论值

图8 扣减仿真测距值之后的测距值

图9 扣减仿真测距值之后的测距值(局部2 h图)
从图8可以看出:实时测距值减去仿真实时距离值后,均值稳定,即按照式(3)可以进行随机误差计算,本次试验算得测距随机误差值为0.09 ns(即距离值为(0.09×10-6)s×(3×108)m/s=0.027 m)。实际卫星在轨运行过程中,测距随机误差平均约为0.5 m,本文方法应用于工程验证中精度可稳定于厘米级,优于实际在轨运行状态,能准确地评估轨道动态条件下卫星测距功能准确度。由于实际在轨时大气阻力、地球引力等变化导致卫星轨道有波动,使用轨道六根数计算相对位置时会产生微小误差,因此在轨实测数据与本文提出的测试数据相比偏大。随着卫星性能的持续发展,测试技术提升也需要同步进行,后续可在动态测距及误差分析方面对测距精度进行进一步的研究和提高。
5 结束语
本文针对距离动态情况下的星间链路测距随机误差测试问题进行研究,提出了基于轨道动态模型的星间链路测距随机误差测试方法。该方法的主要思想为:用星间链路实时测距值减去对应时刻地面仿真实时距离值,获得测距观测残差,然后对该序列取标准差估计,从而实现测距随机误差测试。对星间链路实测测距值采用此方法进行验证,测距随机误差低至0.027 m,与星间链路实测数据吻合较好,与传统三角波动态模拟场景等相比,得到了轨道动态条件下星间测距随机误差更真实的测试结果。
