城市环境下非视距信号探测改正方法
2018-06-06姬生月王振杰
王 翀,姬生月,王振杰
(中国石油大学(华东) 地球科学与技术学院,山东 青岛 266580)
0 引言
全球定位系统(global positioning system,GPS)在20世纪90年代正式投入运行之后,扩展了导航定位、工程测量等领域的测量手段,在陆地、海洋、太空等不同环境中得到了广泛应用[1-4]。随着GPS的现代化和北斗卫星导航系统(BeiDou navigation satellite system,BDS)的快速建设,全球导航卫星系统(global navigation satellite system,GNSS)定位服务的需求量在日常生活中逐渐增加;因此保障定位精度和定位连续性成为重要研究内容。然而,在城市、峡谷等复杂观测环境中,卫星信号遮挡严重,可见卫星数少、卫星星座结构不理想、多路径效应明显,导致定位精度和连续性下降[5-7]。其中非视距(none line of sight,NLOS)信号误差对定位精度的影响最为严重,定位偏差可达数十米[8-10],使得传统定位方法无法满足行人和车辆在城市环境下导航定位的精度要求,限制了GNSS的应用与发展。
城市环境定位中,在已知接收机周围建筑物分布、建筑物几何结构等观测环境信息的前提下,通过对接收机接收到的卫星信号进行传播路径的模拟,可以对卫星信号进行区分,从而判别视距信号与非视距信号,进而对非视距信号误差进行处理[10-12]。近年来,有学者结合3D建筑物模型进行了城市遮挡环境下的定位方法研究,文献[10]建立了Urban Trench模型,利用卫星高度角、方位角信息与建筑物模型对非视距信号进行探测,并对非视距信号进行改正,提高定位精度的同时保证了遮挡环境下足够数量的卫星观测值。
基于上述分析,本文将详细研究Urban Trench方法[10],在重新构造卫星信号遮挡模型的基础上,提出一种改进的Static Trench方法对非视距信号进行探测与改正。基于自主编写的GNSS数据处理程序解算遮挡环境下实测数据,验证非视距信号探测与改正方法的有效性,并对改正前后的定位精度和定位连续性进行比较分析。
1 非视距信号探测与改正模型
1.1 卫星信号遮挡分析
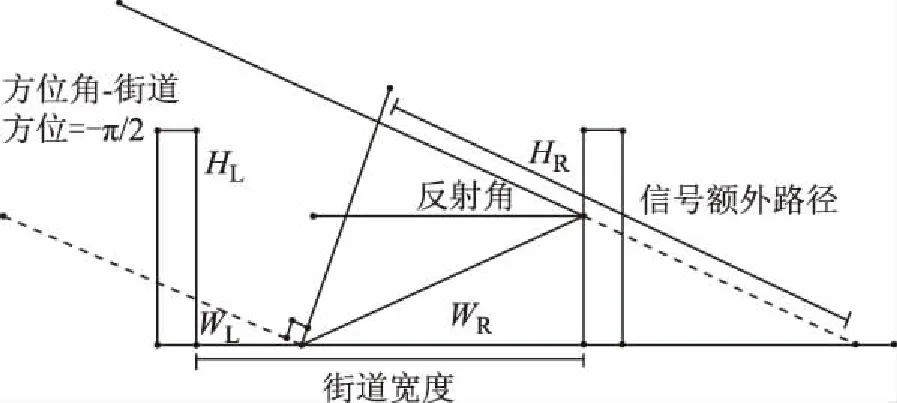
图2 非视距信号传播路径
城市环境中街道两侧建筑物数量多、密度大,信号遮挡与反射现象频繁,非视距信号增多,导致伪距观测值异常,定位精度出现较大偏差[13-14]。假设街道沿直线延伸,两侧建筑物互相平行,卫星信号传播原理如图1所示。待通信2点间视线受阻(虚线细线所示),信号经建筑物反射进入接收机(实线细线所示),产生非视距信号,传播路径如图2所示。其中:Astr为街道方位角;HL和HR分别为街道左侧和右侧的建筑物高度;W为街道宽度;WL和WR分别为接收机到左侧建筑物和右侧建筑物的距离。利用已有信息可构造如下变量:β为卫星方位角与街道方位角差值,用于区分卫星所处街道左侧或右侧;eL和eR分别为左侧和右侧建筑物遮挡下的卫星截止高度角。
1.2 非视距信号探测与改正
遮挡环境下,由于非视距信号的存在,直接对观测数据进行计算会出现较大定位偏差;需要对进入接收机的卫星信号进行处理,对非视距信号进行探测与改正,以保证定位精度。根据非视距信号的产生原因,利用街道两侧建筑物遮挡截止高度角与卫星高度角的关系可对非视距信号进行探测。Urban Trench方法中,街道两侧水平方向180°范围均被定义为建筑物遮挡区域,当卫星高度角低于建筑物遮挡截止高度角,即判断卫星信号为非视距信号。为提高非视距信号正确探测几率,本文结合建筑物实际遮挡情况构造方位角遮挡阈值,对Urban Trench方法进行优化,得到改进的Static Trench方法,如图3所示。其中,aL和aR分别为街道左侧和右侧建筑物对接收机的水平遮挡角度。由图3可见,沿街道方向有一块非视距信号自由区,该区域内无信号遮挡与信号反射。
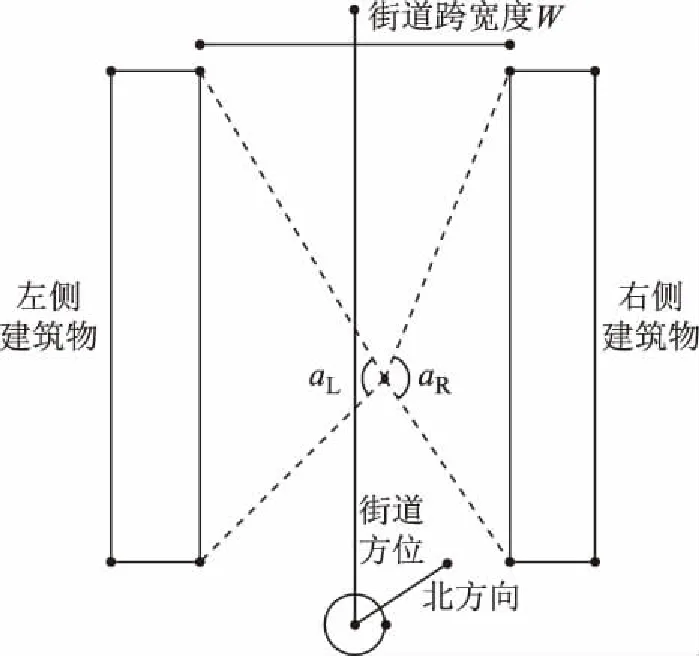
图3 方位角遮挡阈值
非视距信号经反射进入接收机,假设卫星信号在建筑物表面发生镜面反射,结合卫星的方位角和高度角,可以确定信号的反射次数和额外传播距离,理论上信号反射次数不超过3次[10],本文只对信号1次反射情况进行探测与改正,结合图2,得到Static Trench方法改进方位角遮挡阈值后的截止高度角和信号额外传播距离等参数,如表1、表2所示。其中:aL1、aL2和aR1、aR2分别为与街道方位角作差后,左右两侧建筑物的遮挡起止阈值;Δρ为伪距额外传播距离,即非视距信号误差;e为卫星高度角。考虑方位角约束,在卫星高度角小于信号遮挡截止高度角,且大于一次反射高度角的情况下,卫星信号经建筑物一次反射进入接收机,产生非视距信号误差。由图2可知,对伪距观测值,非视距信号相比直射信号存在一段额外传播路径,将信号额外传播距离从非视距信号原始伪距观测值中剔除,即可实现非视距信号的改正,得到正确的伪距观测值。结合建筑物参数信息进行非视距信号探测与剔除过程中,无需得到建筑物绝对位置先验信息,建立接收机与建筑物之间的相对位置模型即可。

表1 Static Trench方法遮挡参数统计

表2 Static Trench方法一次反射参数统计
2 实验与结果分析
2.1 实验概况
本文数据源自青岛中国石油大学(华东)校园遮挡环境实测数据,选取平行建筑物间街道作为实验地点,实验环境如图4所示,数据采集采用Trimble R10接收机。街道方位角及建筑物高度等参数如表3所示。数据处理分别利用原始伪距观测值、剔除非视距信号的伪距观测值、Urban Trench方法及Static Trench方法改正非视距信号误差后的伪距观测值进行伪距单点、差分定位解算。

图4 实验环境

街道宽度参数建筑物高度参数WL/mWR/mHL/mHR/m街道方位角/(°)15.716.822.222.152.8
为验证误差改正模型的有效性,消除定位中滤波方法在历元间的影响,本文采用原始最小二乘方法进行数据解算。在多系统融合定位情况下,基于多模时空统一理论,将不同卫星系统的时间和空间系统进行统一[15-16]。
2.2 非视距信号剔除方法定位结果统计
非视距信号正确探测后可直接剔除或进行改正。为比较非视距信号改正方法与剔除方法的定位精度和定位连续性,验证非视距信号改正方法的优势,本文首先对剔除非视距信号的原始观测值进行计算,得到观测时段内2个实验点非视距信号剔除前后的卫星信息及定位统计结果,如表4、表5所示。非视距信号剔除后,可用卫星数下降,有解历元明显减少。从2个实验点平面坐标均方根(root mean square,RMS)值可以看出,非视距信号剔除后,定位精度显著提升。采用单点定位方法,2个实验点平面RMS值较误差剔除前分别提高20.1 %和37.4 %;为削弱大气误差(电离层误差、对流层误差)和钟差[17],突出非视距信号误差对定位精度的影响,本文又采用差分定位方法对实验数据进行处理,2个实验点平面RMS值分别达到4.04和5.08 m,较误差剔除前分别提高72.7 %和65.5 %。
非视距信号剔除后,定位精度有明显提升;但城市、峡谷等复杂环境中可见卫星数较少,非视距信号的剔除使得卫星信号数量进一步减少,部分历元无法求解定位结果,导致定位连续性下降。
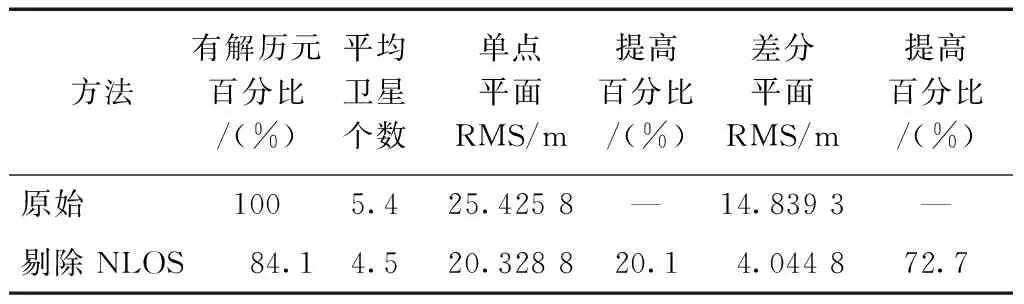
表4 非视距信号剔除定位结果统计(1 391个点)
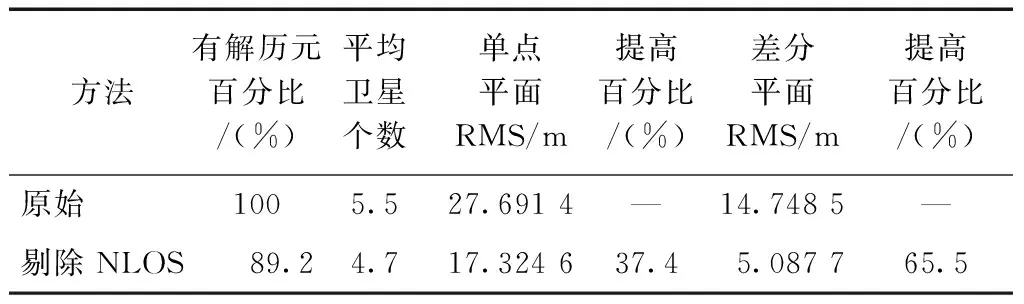
表5 非视距信号剔除定位结果统计(2 017个点)
2.3 非视距信号改正方法定位结果统计
由于城市环境的特殊性,为保证卫星信号数量、提高定位连续性,本文对非视距信号进行改正并保留改正后的非视距信号参与计算。Urban Trench方法对信号额外传播距离进行模拟,从而改正非视距信号误差,进而得到正确的伪距观测值。水平方向上,建筑物对接收机的遮挡采用经验阈值;Static Trench方法优化建筑物遮挡模型,得到更准确的方位角遮挡阈值,从而提高非视距信号正确探测与改正的几率。本实验中Urban Trench 方法和Static Trench方法的实测方位角遮挡阈值如表6所示。观测时段内2个实验点在建筑物遮挡下的卫星星空图如图5、图6所示,在卫星处于遮挡方位角范围内,且高度角小于信号遮挡截止高度角的情况下,卫星信号即可判断为非视距信号。
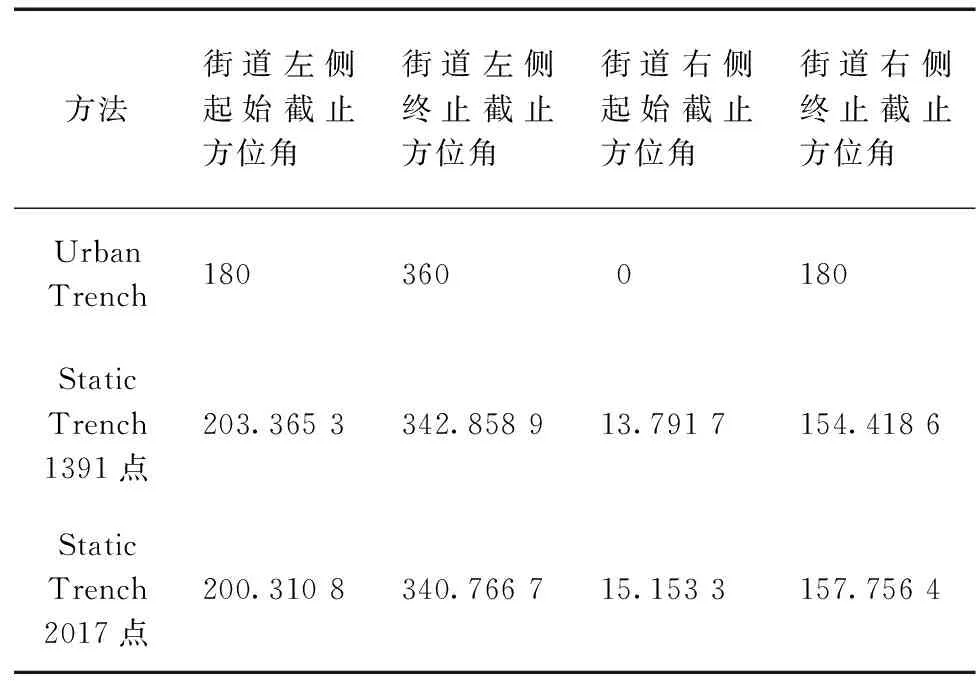
表6 Urban Trench/ Static Trench方法方位角遮挡阈值 (°)
分别采用Urban Trench方法和Static Trench方法,计算得到观测时段内2个实验点非视距信号改正前后的卫星信息及定位统计结果,如表7、表8所示。不同于直接剔除非视距信号,2种方法观测时段内可用卫星数量均没有明显减少,有解历元均大于95 %。从差分定位平面RMS值统计结果可以看出:采用Urban Trench方法,2个实验点平面RMS值分别达到10.74和12.38 m,较误差改正前分别提高27.7 %和16.1 %;采用Static Trench方法,2个实验点平面RMS值分别达到7.59和10.06 m,较误差改正前分别提高48.8 %和31.8 %。

图5 卫星星空图及建筑物遮挡(1 391个点)

图6 卫星星空图及建筑物遮挡(2 017个点)

表7 非视距信号改正定位结果统计(1 391个点)
利用2种方法对非视距信号误差改正后,定位精度均有所提升,Static Trench方法对定位精度的提升更为明显,证明了方法的有效性。结合2.2节实验统计可见:非视距信号误差改正后的定位精度略低于误差剔除后的定位精度;但采用误差改正方法避免了可用卫星数量显著减少,能够保证定位的连续性。

表8 非视距信号改正定位结果统计(2 017个点)
3 结束语
城市遮挡环境下定位误差增大,定位精度明显降低。为实现非视距信号的正确探测与改正,本文在优化Urban Trench方法卫星信号遮挡模型的基础上提出了Static Trench方法,同时采用差分算法突出了非视距信号误差对定位精度的影响。结合建筑物遮挡模型和遮挡环境下的实测数据,对非视距信号探测与改正方法的有效性进行了验证,并对改正前后的定位精度和定位连续性进行了比较分析,结论如下:
1)剔除非视距信号进行定位精度较高,但提高定位精度的同时可用卫星数变少,导致定位连续性下降;
2)Urban Trench方法及Static Trench方法均能够提高遮挡环境下的定位精度、改善定位效果。较原始定位方法,定位精度分别提高约28 % 和49 %,并且可用卫星数量无明显降低,保证了定位连续性;
3)Static Trench方法优化了建筑物遮挡模型,构造了更准确的卫星信号判别阈值。实验结果表明,较Urban Trench方法,Static Trench方法定位精度有明显提高,改善了定位精度与定位连续性不可兼得的情况;
4)采用差分算法更好地削弱了大气误差(电离层误差、对流层误差)、卫星钟差等误差项,突出了非视距信号误差对定位精度的影响,效果优于单点定位中采用误差估计模型对误差项的估计。
利用非视距信号探测与改正模型能有效提高遮挡环境下定位精度、保证定位连续性。为进一步提高遮挡环境下动态测量的定位精度,下一步工作将针对动态测量中非视距信号的探测与改正模型展开研究。
[1] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.
[2] MUELLERSCHOEN R J.NASA’s global DGPS for high-precision users[J].GPS World,2001,12(1):14.
[3] LANDAU H,CHEN X,KLOSE S,et al.Trimble’s RTK and DGPS solutions in comparison with precise point positioning[M].Berlin:Springer Berlin Heidelberg,2009:709-718.
[4] BETAILLE D,PEYRET F,IFSTTAR,et al.Applying standard digital map data in map-aided,lane-level GNSS location[J].Journal of Navigation,2015,68(5):827-847.
[5] HSU L T,CHEN F,KAMIJO S.Evaluation of multi-GNSSs and GPS with 3D map methods for pedestrian positioning in an urban canyon environment[J].Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences,2015(1):284-293.
[6] GU Y,HSU L T,SHUNSUKE K.Passive sensor integration for vehicle self-localization in urban traffic environment[J].Sensors,2015,15(12):30199-220.
[7] 唐卫明,徐坤,金蕾,等.北斗/GPS组合伪距单点定位性能测试和分析[J].武汉大学学报(信息科学版),2015,40(4):529-533.
[8] PEYRAUD S,BÉTAILLE D,RENAULT S,et al.About non-line-of-sight satellite detection and exclusion in a 3D map-aided localization algorithm[J].Sensors,2013,13(1):829.
[9] PEYRET F,BETAILLE D,CAROLINA P,et al.GNSS autonomous localization:NLOS satellite detection based on 3-D maps[J].IEEE Robotics & Automation Magazine,2014,21(1):57-63.
[10] BETAILLE D,PEYRET F,ORTIZ M,et al.A new modeling based on urban trenches to improve GNSS positioning quality of service in cities[J].IEEE Intelligent Transportation Systems Magazine,2013,5(3):59-70.
[11] MIURA S,HISAKA S,KAMIJO S.GPS positioning with multipath detection and rectification using 3D maps[J].Seisan Kenkyu,2014,66:109-115.
[12] HSU L T,GU Y,KAMIJO S.3D building model-based pedestrian positioning method using GPS/GLONASS/QZSS and its reliability calculation[J].GPS Solutions,2016,20(3):413-428.
[13] WANG L,GROVES P D,ZIEBART M K.GNSS shadow matching:improving urban positioning accuracy using a 3D city model with optimized visibility scoring scheme[J].Navigation - Journal of the Institute of Navigation,2013,60(3):195-207.
[14] GU Y,HSU L T,KAMIJO S.Passive sensor integration for vehicle self-localization in urban traffic environment[J].Sensors,2015,15(12):30199-30220.
[15] 高星伟,过静珺,程鹏飞,等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报,2012,41(5):743-748.
[16] 李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模融合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.
[17] 党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京:测绘出版社,2007.
