基于截尾全变差Retinex算法的图像复原技术

蒋 阳，曹 杰，豆泽阳，肖宇晴，汤 磊，郝 群,3

(1.北京理工大学光电学院 机器人与系统教育部重点实验室, 北京 100081;2.中国兵器科学研究院， 北京 100089; 3.清华大学深圳研究生院， 深圳 518055)

图像增强是指通过有选择地突出某些感兴趣区域，方便人或机器进行分析,同时抑制一些冗余信息,提高图像质量和使用价值。目前，图像增强技术已广泛应用于水下增强、跟踪识别、航空航天等领域[1]。但由于实际环境中受到照明非均匀尤其是阴影的影响，使在强烈明暗环境下图像增强困难。

基于人类视觉路径，Land和McCann[2]首次提出了Retinex理论，作为人类视觉系统(HSV)的颜色感知模型能够提高图像非均匀性，但基于此模型的多路径搜索Retinex算法[3]复杂度较大且参数较多，实际操作性不强。Park[4]等使用了Retinex模型对低光照图像进行增强。李益红[5]提出了一种多分辨多尺度的彩色Retinex图像增强算法。在基于PDE的模型[6]中，Retinex原则通常被转化为物理形式并基于泊松方程建模，仅使用两个快速傅里叶变换产生准确结果。该算法类型的主要假设是反射率作为图像中的尖锐细节，而照明变化平滑。基于该假设，豆泽阳等[7]提出了Retinex问题的变指数模型，Ma等[8]提出了使用相同假设的全变差(Total variation)和非局部全变差正则化模型，Ng[9]使用更多的限制条件应用在TV模型，梁和张[10]建立了一种新的高阶总变化L1分解模型(HoTVL1)，可以校正分段线性阴影，Zosso[11]提出了基于非局部差分算子的统一Retinex模型。

然而，上述Retinex模型基本均以假设空间光照渐变为基础，没有突变部分。实际上许多具有非均匀照明的图像具有突变的光照，突变部分形成强烈的阴影反差，引起图像质量大幅下降。因此，本研究针对该问题，提出可适用于光照变化剧烈的假设，并根据该假设，提出一种使用截尾全变差Retinex模型，其中，假设截尾全变差的照明函数属于有界变差函数空间。

1 截尾全变差Retinex模型

针对非均匀照度中存在剧烈变化的情况提出如下假设：① 物体为博朗反射体，且反射率对应于图像中的尖锐细节；② 大多数区域的照明是渐变的，但也可能含有突变部分。本文基于灰度图像制定和讨论模型，对于彩色图像，本文算法将RGB颜色空间映射到HSV(色调，饱和度，色彩值)颜色空间中，仅处理V通道，然后将其转换回RGB域。这种方法称为HSV Retinex[9]。

假设待求的光照图像为u，则基于截尾全变差(Truncated Total Variation)的正则项表达式为：

(1)

其中

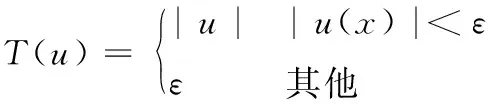
(2)

其中(ux,uy)为图像U的梯度。由式(2)可以看出，截尾全变差正则项仅惩罚梯度幅度小于阈值ε的梯度，对于梯度幅度大于ε的值则予以保留，因此保留住了光照图像中的突变部分。图1显示了全变差和截尾全变差形状。与全变差相比，截尾全变差的形状看起来像全变差的“截尾”版本。

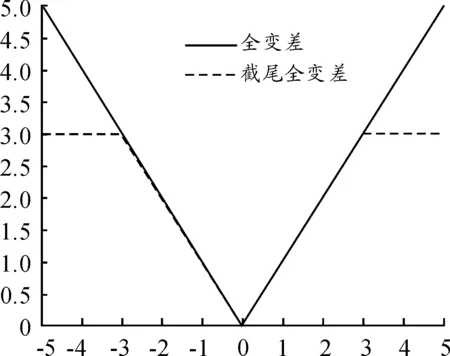
图1 全变差与结尾全变差

由于截尾全变差是非凸的，直接求解此正则项较为困难。注意到式(2)可以使用稀疏正则化L0范数重新表达，转为有益于算法有效实现的形式。将ε作为参数，则式(2)可写为

(3)

其中|·|0为：当l≠0时，|l|0=1,否则|l|0=0。

Retinex理论的主要目标是将真实图像F分解为反射图像R和照明图像U，即F=R·U,已知真实图像F，求出阴影图像即可得出恢复后的图像R。基于所提新的假设，照明图像可能包含非平滑部分，本研究使用截尾全变差正则项建立Retinex模型。设u为阴影图像，f为真实图像，则所需优化的目标函数为：

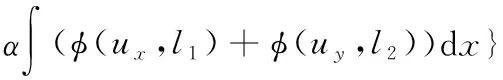
(4)

式(4)右边第一项是图像数据保真项，第二项是截尾全变差。与其他平滑模型相比，截尾全变差在细节平滑和强边缘保留之间取得了良好的平衡，而基于传统光照假设设计的正则项有些降低了强边缘。模型可使用分裂Bregman方法求解。

2 模型优化

由于涉及L1和L0正则化惩罚项，直接优化目标函数(4)相对比较困难。因此，本文引入交替的优化策略与Split Bregman框架，其主要思想是引入辅助变量扩展原来的项并交替更新。

针对截尾全变差项中ux-l1和uy-l2分别引入两个对偶变量b1和b2，则目标函数(4)可以重新表达为：

(5)

其中，约束条件为

b1=ux-l1,b2=uy-l2

(6)

利用Bregman距离并将有约束问题转化为无约束问题，式(5)可以写为：

(7)

本研究将上述联合优化问题通过式(7)解耦到几个子问题交替解决，求解步骤描述如下：

步骤1：固定l1,l2,b1,b2,t1,t2优化u。该子问题描述为：

(8)

由于函数可微，可得其欧拉-拉格朗日方程为

(9)

其中，Δ为拉普拉斯算子。方程(9)可以通过使用Gauss-Seidel迭代算法或FFT算子有效求解。

步骤2：固定u,l1,l2,t1,t2，计算b1和b2。该子问题的唯一最小化可以通过应用收缩算子获得：

(10)

(11)

其中，

(12)

步骤3：固定u,l1,l2,b1,b2，更新t1,t2。描述如下：

(13)

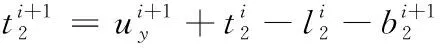
(14)

步骤4：固定u,t1,t2,b1,b2，更新l1,l2。可得：

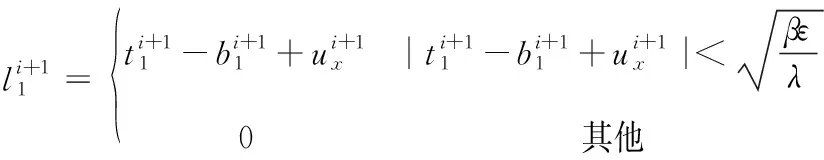
(15)

(16)

3 实验结果与分析

本文针对所提算法进行三组实验，每组实验都使用本文方法与全变差、二阶全变差以及多尺度Retinex方法进行比较分析。其中，实验一采用仿真方法，实验二、三采用真实图像复原。

实验一将没有阴影的原始图像中模拟添加阴影，如图2(a)所示为人工合成带有阴影的图像。对图2(a)使用全变差、二阶全变差以及多尺度Retinex方法与所提算法对其进行实验对比，实验结果对应如图2(b)、图2(c)、图2(e)，可以看到本文所提方法使得图像复原结果最优，阴影信息基本消除。为进一步量化对比，本文使用结构相似指数(SSIM)和CIEDE2000色差分别测量原始图像和恢复图像之间的纹理相似度和感知差异，如表1所示，所提方法显著优于其他方法。

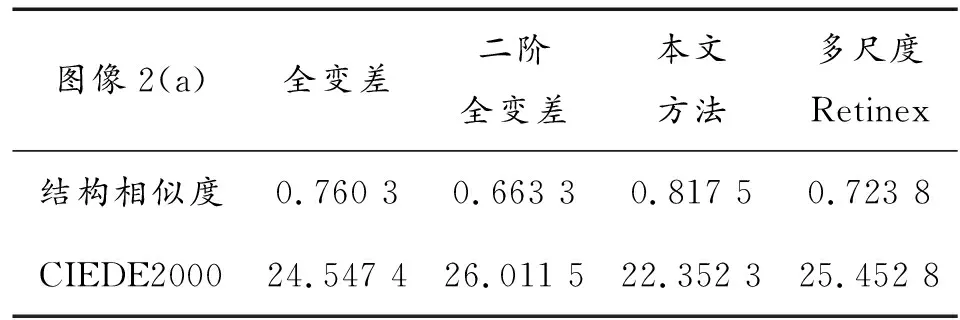
表1 多种算法的SSIM及CIEDE2000结果对比

实验二使用真实图像进行复原，如图3(a)所示，为真实阴影图像，对比算法优化结果见图3(b)、图3(c)、图3(e)，可以看到本文所提方法几乎去除了所有阴影，而对比的算法优化依然留有阴影痕迹。

为进一步验证所提模型的鲁棒性，使用阴影更深的真实图像进行复原，如图3(f)所示，实验方法同实验一、实验二，本文优化结果见图3(i)，对应的实验结果见图3(g)、图3(h)、图3(j)，可以看到本文所提方法与实验一、二取得了相似的结果。

图2 仿真阴影图像优化结果

图3 真实阴影图像优化结果

4 结论

传统Retinex模型对光照图像建模时都假设其是渐变的，没有强烈阴影。然而，许多具有非均匀照明的图像实际上具有非平滑的光照。本文针对该问题提出新的假设，即：① 反射物体为博朗反射体且反射率对应于图像中的尖锐细节；② 大多数地区的光照光滑，但可能含有不平滑的部分。基于新的假设，本文提出截尾全变差Retinex模型用于真实图像复原中。

实验表明，本文所提算法在图像细节平滑和边缘保留之间取得了良好的平衡，对于去除非均匀照明、减少晕圈伪影效果显著。虽然本文的假设与模型是针对具有强烈对比阴影的情况提出的，但实验表明它也可以应用于一般退化的图像，并显著减少光晕伪影。

[1] ZHANG S,WANG T.Underwater Image Enhancement via Extended Multi-Scale Retinex[J].Neurocomputing,2017,245.

[2] LAND E H,MCCANN J J.Lightness and retinex theory.J Opt Soc Am[J].Journal of the Optical Society of America,1971,61(1):1-11.

[3] MARINI D,RIZZI A.A computational approach to color adaptation effects[J].Image & Vision Computing,2000,18(13):1005-1014.

[4] PARK S,YU S,MOON B,et al.Low-light image enhancement using variational optimization-based retinex model[J].IEEE Transactions on Consumer Electronics,2017,63(2):178-184.

[5] 李益红,周晓谊.一种多分辨多尺度的Retinex彩色图像增强算法[J].计算机工程与应用,2017,53(16):193-198.

[6] HAO W,HE M,GE H,et al.Retinex-Like Method for Image Enhancement in Poor Visibility Conditions[J].Procedia Engineering,2011,15:2798-2803.

[7] DOU Z,GAO K,ZHANG B,et al.Realistic image rendition using a variable exponent functional model for Retinex[J].Sensors,2016,16(6):832.

[8] MA W,MOREL J M,OSHER S,et al.An L1-based variational model for Retinex theory and its application to medical images[C]// Computer Vision and Pattern Recognition.IEEE,2011:153-160.

[9] NG M K,WANG W.A Total Variation Model for Retinex[J].Siam Journal on Imaging Sciences,2011,4(1):345-365.

[10] LIANG J,ZHANG X.Retinex by Higher Order Total Variation L1 Decomposition[M].Kluwer Academic Publishers,2015.

[11] ZOSSO D,TRAN G,OSHER S J.Non-Local Retinex—A Unifying Framework and Beyond[J].SIAM Journal on Imaging Sciences,2015,8(2):787-826.