初探数形结合方法在高中数学教学中的运用

江苏省泰兴市第四高级中学 孙建新

高中的所有数学思想方法中，数形结合思想是一种始终贯穿高中数学的数学思想方法。它的关键在于用代数的方法解决一些复杂的几何问题，用简便的几何方法解决一些复杂的代数问题，这样可以将代数和几何这两个完全不搭边的名词及其所代表的范畴进行了有效的连接，可以让学生在大脑意识形态里面建立起代数与图形互相转换的概念，重点培养解决问题方法的多样性、简便性、发散性。

一、用具体的图形辅助复杂的代数问题

数形结合的思想方法的重要作用之一就是用具体的图形辅助复杂的代数问题。用几何的本质来反映、解决复杂的代数问题是数形结合思想的重要运用。我们用具体的数学例子来进行说明。

例1 已知，若的最小值记作写出g（t）的表达式。

解析：由于，所以抛物线的

对称轴为开口是向上的。

1.当时，（fx）在[t,t+1]上单调递增，如图1所示。

所以当x=t时，f（x）最小，即

2.当上递减，

在上递增，如图2所示。

所以当

3.当在[t,t+1]上单调递减，如图3所示。

所以当x=t+1时，f（x）最小，即f（x）

综合①②③可知：

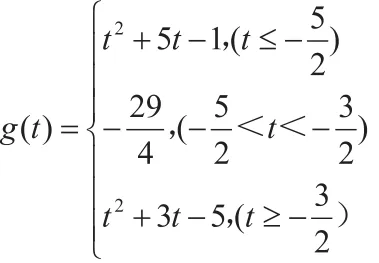
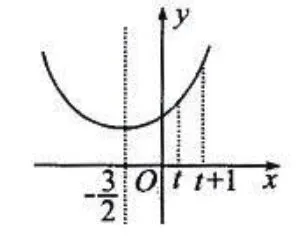
图 1

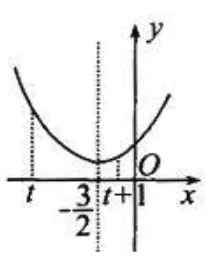
图 2

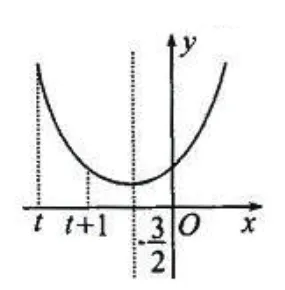
图 3

例题总结：通过二次函数的图象我们可以确定解题的思路，我们可以更加直观、明确、清楚、清晰地体现数形结合的优越性。但是需要我们特别注意的是，对于二次函数在闭区间上的最大值、最小值问题，最重要的是应该抓住对称轴和所给定区间的相对位置关系进行分类讨论和仔细解决。第一步要确定的是对称轴与对称区间的位置关系，结合函数图象确定在封闭区间的单调情况，然后再确定是在什么位置取得最值。

方法总结：对含有参数的问题利用数形结合思想。第一，解决这类问题时要准确画出大致的函数图象，注意函数的定义域（非常重要）。第二，用图象法讨论方程（特别是含参数的方程）解的个数是一种非常有效的方法，值得注意的是首先把方程两边的代数式看作两个函数的表达式（有时可能先做适当调整，这样以便于画图），然后作出两个函数的图象，根据图然后求解。第三，在运用数形结合思想分析问题和解决问题时，需做到以下四点：首先，要准确理解一些概念和运算的几何意义以及曲线的代数特征；其次，要恰当设定参数，合理利用参数，建立相互之间的关系，然后做好转化；再者，正确确定参数的取值范围，以防重复和遗漏，思路一定要清晰；最后，“数”与“形”紧密联系起来，使一些较难解决的代数问题几何化、困难的几何问题代数化，便于问题得以解决。

二、用代数方法解决复杂的几何问题

我们经常用到的就是空间向量的代数式子将复杂不容易看见的、不容易解决的几何问题进行简便化。

例2 如图4所示，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点。证明：（1）AE⊥CD；（2）PD⊥平面ABE。

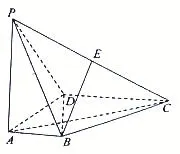
图4

证明：AB、AD、AP两两垂直，建立如图所示的空间直角坐标系，设PA＝AB＝BC＝1，则P（0,0,1）。

（1） ∵∠ABC＝60°，∴△ABC为正三角形，

∴C（12，32，0），E（14，34，12），

设D（0，y,0），由AC⊥CD，得即y＝ 233，则D（0，233，0），

∴＝（－12，36，0），又＝（14，34，12），

∴·＝－12×14+36×34＝0，

∴⊥，即AE⊥CD。

（2）方法一：

∵P（0,0,1），∴＝（0，233，－1），

又＝34×233+12×（－1）＝0，

∴⊥，即PD⊥AE，

＝（1,0,0），∴·＝0，

∴PD⊥AB，又AB∩AE＝A，∴PD⊥平面AEB。·

方法二：

＝（1,0,0），＝（14，34，12），

设平面ABE的一个法向量为n＝（x，y，z），

则x＝0，14x+34y+12z＝0，

令y＝2，则z＝－3，

∴n＝（0,2，－3），

∵＝（0，233，－1），

显然＝33n。

∵∥n，

∴⊥平面ABE，即PD⊥平面ABE。

三、高考题型涉及数形结合思想的题型

（1）集合问题中Venn图（韦恩图）的运用；

（2）数轴及直角坐标系的广泛应用；

（3）函数图象的应用；

（4）数学概念及数学表达式几何意义的应用；

（5）解析几何、立体几何中的数形结合。

四、在运用数形结合思想分析解决问题时，要遵循以下三个原则

①等价性原则。要注意由于图象不能精确刻画数量关系所带来的负面效应；

②双方性原则。既要进行几何直观分析，又要进行相应的代数抽象探求，如果仅仅对代数问题进行几何分析容易出错，容易漏掉；

③简单性原则。不要一味地为了“数形结合”而进行数形结合，在具体运用时，首先要考虑方法是否可行；其次是要选择一个很好的突破口，合理设定参数、运用参数、建立数形结合的关系，做好转化；最后是要善于挖掘隐含的条件，准确确定参变量的取值范围，特别是运用函数图象时，应设法选择动直线与固定的二次曲线为最好的方法。

综上所述，要想真正把数形结合思想彻底弄清楚，那么就需要多去练习这样的题目，在大脑里面建立自己的做题体系。