千斤顶偏心荷载作用下盾构隧道管片裂纹扩展规律

苏 昂

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

盾构法以安全、高效的特点，成为城市地铁最主要的施工方法[1]。随着城市地铁规模的不断扩大，地铁穿越地层的地质条件愈加复杂，施工过程中质量问题逐渐增多。我国广州、深圳、福州等东南沿海地区的地层具有上软下硬的特点，盾构机在穿越该类地层时，盾构姿态控制不佳，容易造成千斤顶偏心，管片应力集中程度较高，容易导致管片裂损等问题。

国内学者及工程研究人员对盾构隧道裂损病害进行了大量研究。封坤等[2]依托南京长江隧道，研究了大型水下盾构隧道在不同拼装方式下的破坏特征。陈俊生等[3]采用足尺试验和三维有限元软件模拟施工阶段管片开裂过程，得出开裂和破损是由管片间相对扭转所致。张学文[4]整理了南京地铁区间隧道衬砌病害数据，分析了运营期隧道病害的状态及成因。竺维彬等[5]对广州地铁1号线和2号线进行比较，分析了管片生产、施工、使用过程中的开裂原因。秦建设等[6]从盾构机与管片相互作用入手，研究得出盾构机姿态与衬砌走向不协调导致了管片错台及混凝土开裂。叶耀东等[7]依据上海地铁区间隧道监控数据，分析了病害原因。宋克志等[8]针对施工期管片出现破损的现象，分析管片局部破损的原因。张建刚等[9]针对施工阶段管片衬砌开裂破损的现象，通过建立三维有限元模型，系统分析了管片结构在千斤顶推力作用下的力学响应特性，给出了管片开裂的主要原因。

以上针对盾构隧道裂损病害的研究，大部分基于室内试验和经验类比法，定性分析隧道开裂因素，只有少部分采用数值模拟方法。现阶段的数值模拟研究多将管片视作连续介质，根据管片应力集中程度，预判管片裂纹形态和可能出现位置，进而分析管片开裂原因。然而，管片的开裂具有很强的随机性，无法准确预判开裂位置。同时，管片裂纹的扩展具有很强的不确定性，采用现阶段的数值模拟方法无法描述裂纹扩展规律和扩展路径。

鉴于此，本文将开裂后的管片看作非连续介质，基于扩展有限元理论[10-11]，利用ABAQUS软件建立管片精细化三维数值模型，分析千斤顶偏心时管片裂纹形态、扩展规律和扩展路径。

1 工程概况

该地铁位于东南沿海地区，沿线地貌形态为山前冲积平原及河流冲淤积平原，部分地段为剥蚀残山。与北京、上海等地层相对单一的城市相比，该地铁沿线地质条件表现出地形起伏多变、地层上软下硬、岩性复杂多样的特征。

该地铁工程管片环外径6.2 m，内径5.5 m，管片厚度350 mm，幅宽1.2 m，管片衬砌结构采用“3+2+1”分块方式。管片环间设置凹凸榫，凸榫端部宽为127 mm，凹槽内部宽为135 mm，环间凹凸榫连接时凸榫在凹槽中有8 mm调整余量。管片构造如图1所示。管片采用错缝拼装，施工过程中若遇到不良施工荷载，极易造成管片损伤[12]。

图1 管片构造(单位：mm)

2 数值模拟

2.1 模型的建立

为简化计算模型，将千斤顶推力转换成均布荷载施加在靴板上，相邻管片侧面之间的接触不是简单的铰接或固定端约束，而是挤压和分离同时存在的复杂接触，在管片两侧设置2个基座用于准确模拟这种复杂的边界条件[13]。管片模型见图2。

图2 管片模型

基座采用全约束，管片与基座之间在法向上设为硬接触，管片之间可以传递压力，允许接触后分离，在切向上采用基于罚函数的库仑摩擦模型。凸榫端面不加约束，凹槽端面沿着纵向施加位移约束，切向和径向无约束。

2.2 参数的选取

管片混凝土弹性模量为2.648×104MPa，泊松比为0.167，剪胀角为15°，偏心率为0.1，双轴与单轴压缩强度比为1.16，屈服常数为 0.666 7，混凝土的压缩拉伸特性见表1[14]。管片与基座之间的摩擦系数为0.3～0.4，为了反映普遍情况取平均值0.35。管片与靴板间的摩擦系数因其表面粗糙度不同且变化较大，取0.35[13]。

2.3 模拟工况

模拟盾构机3个千斤顶沿着径向同时向管片内弧面或外弧面偏移3 cm。按照实际施工参数，千斤顶荷载为15 MPa。千斤顶荷载工况见表2。

表1 混凝土压缩拉伸特性

表2 千斤顶荷载工况

3 结果分析

3.1 裂纹形态及位置

千斤顶向管片内、外弧面偏心时管片裂纹形态分别见图3、图4。可以看出：① 2种偏心作用下裂纹均集中出现在管片左侧部位，管片的内、外弧面，顶面及侧面均出现大范围网状开裂，且管片边缘、角部出现开裂，存在脱落、掉块等风险。②千斤顶向内弧面偏心时管片裂纹范围更广、裂纹数量更多、危害更严重。其原因：管片内弧面分布有手孔及螺栓孔，一定程度上提高了管片局部应力集中程度，同时还为管片的局部变形和裂纹扩展提供了空间，从而扩大了管片裂纹的扩展范围。

图3 千斤顶向内弧面偏心时管片裂纹形态

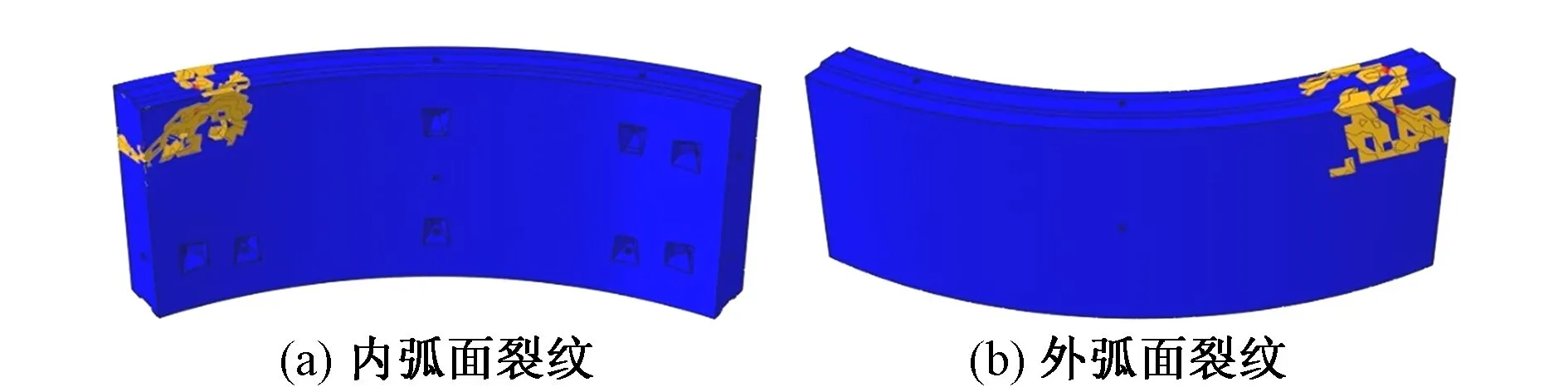
图4 千斤顶向外弧面偏心时管片裂纹形态

2种工况初始裂纹位置存在差异，见图5。千斤顶向内弧面偏心时初始裂纹出现在凸榫内侧边缘，千斤顶向外弧面偏心时初始裂纹出现在凸榫外侧边缘，2种 工况初始裂纹均出现在千斤顶偏心一侧的凸榫边缘。 这是由于千斤顶的中心与管片环的中心不重合时管片处于偏心受压状态，千斤顶偏心一侧管片局部应力集中程度相对更高。

图5 2种工况初始裂纹位置

3.2 裂纹扩展规律

图6为千斤顶向内、外弧面偏心时管片压缩量随裂纹长度变化曲线。可以看出：2种工况裂纹长度均呈台阶式递增，管片在新裂纹产生之前需要一定程度的能量积累。裂纹扩展可分为裂纹初始形成、裂纹协调发展、裂纹迅速发展3个阶段。内弧面偏心工况管片裂纹扩展的3个阶段分别对应OA段、AB段、BC段，外弧面偏心工况管片裂纹扩展的3个阶段分别对应OD段、DE段、EF段。

图6 偏心荷载作用下管片压缩量随裂纹长度变化曲线

第1阶段为裂纹初始形成阶段(OA段和OD段)。加载初期，管片内部应力、应变较小，未引起管片开裂。当内弧面、外弧面偏心工况的管片压缩量分别达到0.029,0.018 mm时，裂纹才开始出现。内弧面手孔给内弧面提供了相对较大的变形空间，使得内弧面偏心工况的管片压缩量大于外弧面偏心工况。总体而言，该阶段2种工况的管片压缩量均较小。

第2阶段为裂纹协调发展阶段(AB段和DE段)。该阶段裂纹长度随着管片压缩量的增大而增长。该阶段结束时，内弧面偏心工况的管片压缩量为0.125 mm，裂纹总长度为590 mm;外弧面偏心工况的管片压缩量为0.106 mm，裂纹长度为754 mm。

第3阶段为裂纹迅速发展阶段(BC段和EF段)。该阶段裂纹发展迅速，绝大多数的裂纹均在该阶段扩展。内弧面偏心工况的管片裂纹长度从590 mm发展到 6 290 mm，外弧面偏心工况的管片裂纹长度从754 mm 发展到 5 032 mm。管片压缩量基本保持不变，但裂纹长度持续增大，表明管片结构已经出现区域性破坏，承载能力已受到较大影响。

3.3 裂纹扩展路径

千斤顶向内弧面偏心工况管片裂纹扩展过程见图7。加载初期管片内部应力、应变较小，未引起管片开裂。当管片压缩量达到0.029 mm时管片凸榫内侧边缘出现首条裂纹(见图7(a))，并沿径向朝外弧面扩展。随着千斤顶荷载的增大，管片外弧面、内弧面、侧面先后出现首条裂纹(见图7(b)—7(d))，且内、外弧面裂纹均沿斜向45°向着管片侧面延伸扩展，从而形成剪切裂纹，引发管片边角破坏(见图7(e))。随后，管片外弧面、内弧面、侧面、顶面裂纹迅速发展，外弧面裂纹向着管片中部发展，内弧面裂纹则延伸贯穿手孔，侧面裂纹向着内弧面方向发展，顶面裂纹沿着凸榫方向发展，外弧面、内弧面、侧面、顶面裂纹交汇贯通形成最终的大范围网状裂纹(见图7(f))。

图7 千斤顶向内弧面偏心工况管片裂纹扩展过程

4 结论

1)2种偏心作用下管片裂纹形态均表现为内弧面、外弧面、顶面与侧面大范围网状开裂。千斤顶向内弧面偏心时裂纹范围更广、数量更多、危害更严重。

2)在千斤顶偏心荷载作用下，管片偏心受压，导致管片局部应力集中程度显著升高，引起管片开裂破损，初始裂纹均出现在千斤顶偏心一侧的凸榫边缘。

3)裂纹长度呈台阶式递增。裂纹扩展可以分为裂纹初始形成、裂纹协调发展、裂纹迅速发展3个阶段。绝大多数的裂纹发生在第3个阶段，该阶段管片结构出现区域性破坏。

[1]何川，封坤，方勇.盾构法修建地铁隧道的技术现状与展望[J].西南交通大学学报(自然科学版)，2015，50(1)：97-109.

[2]封坤，何川，苏宗贤.南京长江隧道管片衬砌结构原型加载试验[J].中国公路学报，2013，26(1):135-143.

[3]陈俊生，莫海鸿，梁仲元.盾构隧道施工阶段管片局部开裂原因初探[J].岩石力学与工程学报，2006，25(5)：906-910.

[4]张学文.运营期地铁隧道常见结构病害成因及治理方法研究[D].南京：南京大学，2014.

[5]竺维彬，鞠世健.盾构隧道管片开裂的原因及相应对策[J].现代隧道技术,2003,40(1):21-25.

[6]秦建设，朱伟，陈剑.盾构姿态控制引起管片错台及开裂问题研究[J].施工技术,2004,33(10):25-27.

[7]叶耀东,朱合华,王如路.软土地铁运营隧道病害现状及成因分析[J].地下空间与工程学报，2007，3(1):157-160.

[8]宋克志，袁大军，王梦恕.盾构法隧道施工阶段管片的力学分析[J].岩土力学,2008,29(3):619-628.

[9]张建刚,何川,肖明清.大型管片衬砌结构受千斤顶推力作用的裂缝分析[J].铁道建筑，2008,48(4):28-31.

[10]DUARTE C A，ODEN J T.Anh-pAdaptive Method Using Clouds[J].Computer Methods in Applied Mechanics and Engineering，1996，139(1):237-262.

[11]BELYTSCHKO T，BLACK T.Elastic Crack Growth in Finite Elements with Minimal Remeshing[J].International Journal for Numerical Method in Engineering,1999，45(5):601-620.

[12]宋成辉.软土地层地铁盾构通用环管片结构设计研究[J].地下空间与工程学报，2011，7(4):733-740.

[13]CHEN J S,MO H H.Numerical Study on Crack Problems in Segments of Shield Tunnel Using Finite Element Method[J].Tunnelling and Underground Space Technology,2009，24(1):91-102.

[14]卢岱岳，何川，王士民，等.千斤顶作用下带榫管片的裂纹扩展规律[J].西南交通大学学报(自然科学版)，2017，52(1)：75-82.