装配式宽幅连续T梁剪力滞效应研究
2018-06-04安平和时元绪邬晓光肖凯龙
安平和,时元绪,邬晓光,肖凯龙
(长安大学 公路学院,陕西 西安 710064)
近几十年来,国内外诸多学者致力于剪力滞效应的研究,主要集中在理论解析、数值分析、试验模型以及有效分布宽度的研究上,而且对于箱梁研究较多[1-2],对于装配式宽幅连续T梁研究较少。其中,文献[3-4]提出结合基于剪切变形规律的剪力滞翘曲位移函数和翼板变厚度的箱梁剪力滞效应分析方法。文献[5-6]先后提出了分析箱形梁剪力滞效应的有限元法。文献[7-9]进行了薄壁箱梁剪力滞效应分析。文献[10-12]为了研究预应力对箱梁桥剪力滞效应的影响,通过实体有限元、试验方法进行分析。文献[13-14] 发现预应力钢束的弯起角是影响剪力滞系数的主要因素,但是能否抵消剪力滞效应没有具体结论。文献[15]发现预应力钢束对箱梁底板应力影响较为明显,而对顶板没有影响。
但是目前关于装配式宽幅连续T梁剪力滞效应突出位置的研究较少,另外针对普通钢筋和预应力钢束对剪力滞效应影响的研究也不充分。本文针对这2部分研究不足建立实体有限元模型,并通过理论分析,深入研究剪力滞效应突出位置和普通钢筋、预应力钢束的配置是否能抵消剪力滞效应。
1 装配式宽幅连续T梁剪力滞效应分布特点
四跨一联的装配式T梁桥在我国应用广泛。为了使本文分析具有代表性,现取四跨一联装配式宽幅连续T梁桥,宽跨比为0.75,主梁跨径为4×20 m,每片主梁宽2.4 m,高为1.5 m,每跨设置4道横隔板。在调研过程中发现,支点顶部裂缝较为严重,尤其是中梁现浇段支点附近。建立素混凝土有限元实体模型,对于梁体连接处现浇混凝土,由于采用先简支后连续的施工方法,体系转化为连续梁以后,其荷载作用为二期恒载和活荷载。通过实体有限元模型分析T梁不同位置上翼缘的正应力分布规律。
对于装配式宽桥而言,横向各梁的应力分布规律基本一致,呈现中梁稍大于边梁的趋势。现以中梁作为分析对象,取边跨1/4处、边跨跨中、边跨支点、中跨1/4处、中跨跨中和中跨支点6个不同位置分析上翼缘的正应力分布规律,其正应力分布规律如图1。

图1 不同位置上翼缘正应力分布
由图1可知:边跨1/4处、边跨跨中、中跨1/4处和中跨跨中上翼缘正应力分布较为均匀,剪力滞效应不明显。边跨支点、中跨支点负弯矩区拉应力分布不均匀,剪力滞效应明显,且均为正剪力滞效应。在支点负弯矩区,由于存在正剪力滞效应,支点顶部拉应力容易使上翼缘混凝土开裂。
2 普通钢筋和预应力钢束对剪力滞效应的影响
由上述剪力滞效应分布特点研究得出边跨支点、中跨支点上翼缘剪力滞效应明显。因此,下面只针对支点上翼缘正应力进行分析。
2.1 普通钢筋对剪力滞效应的影响
建立钢筋混凝土有限元实体模型,通过改变T梁承托到支点范围内的上翼缘普通钢筋直径来分析装配式宽幅连续T梁支点上翼缘正应力分布规律。
取3组不同钢筋直径12,18,25 mm。将正应力分布汇成折线如图2。
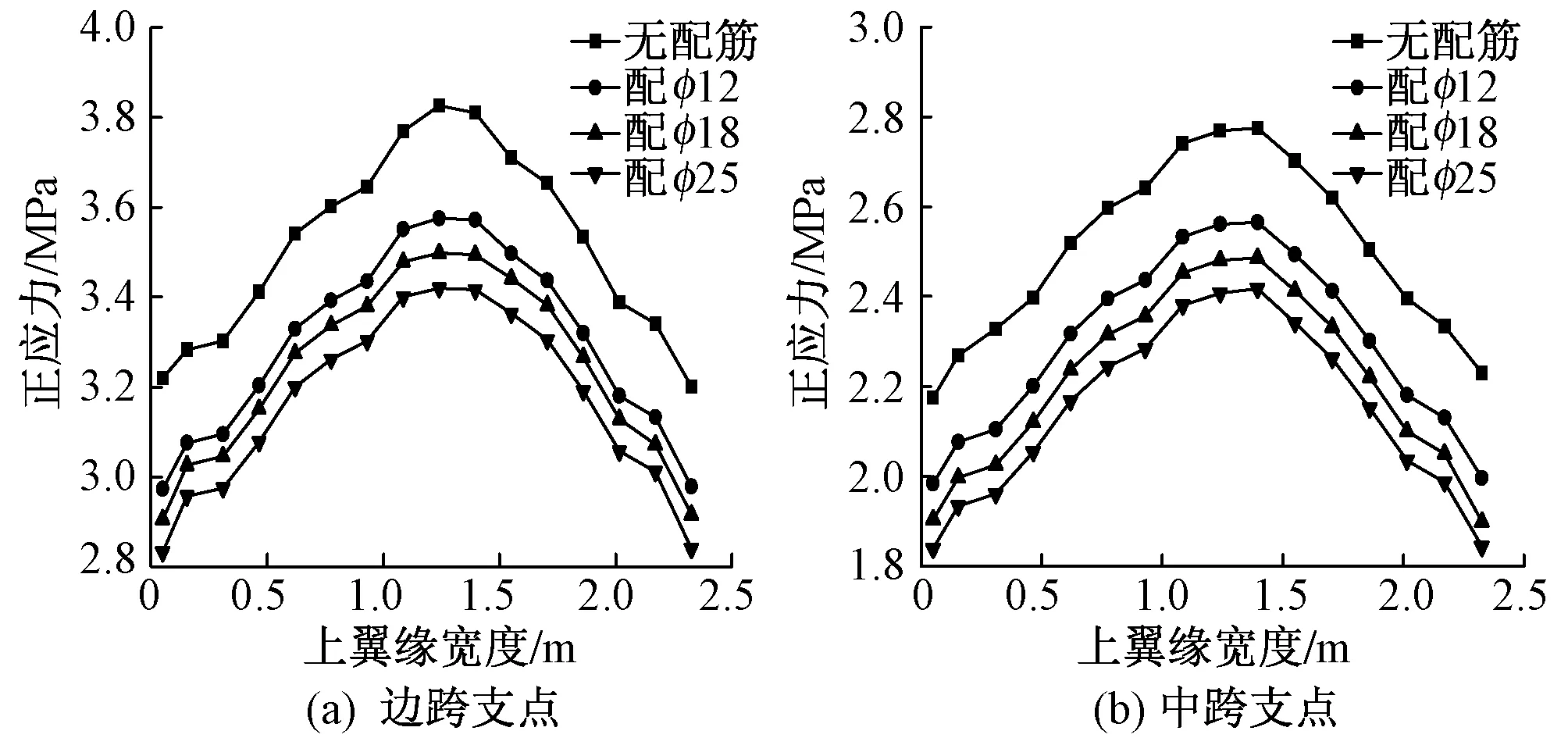
图2 支点上翼缘正应力分布
由图2可知:普通钢筋能够减小支点上翼缘的拉应力值,拉应力整体减小且幅值较小,通过改变钢筋直径基本无法改变支点处混凝土梁的受力。另外应力极大值与极小值差值在配置普通钢筋后基本没有改变,其值约为0.6 MPa。支点上翼缘仍然存在剪力滞效应,且为正剪力滞效应。因此,配置普通钢筋对于剪力滞效应基本没有影响。
2.2 预应力钢束对剪力滞效应影响研究
建立预应力混凝土有限元实体模型,取预应力钢束不同布置位置、不同股数来分析连续T梁桥支点上翼缘正应力分布规律。取3组不同预应力钢束股数,第1组:T1为5股、T2为3股;第2组:T1为5股、T2为4股;第3组:T1为5股、T2为5股。另外,改变预应力钢束横向布置位置,在T1为5股、T2为3股的基础上,梁肋顶部中间位置增加T3且为3股。负弯矩预应力钢束横断面布置如图3所示。

图3 负弯矩预应力钢束横断面布置(单位:mm)
将其正应力分布汇成折线图,见图4。
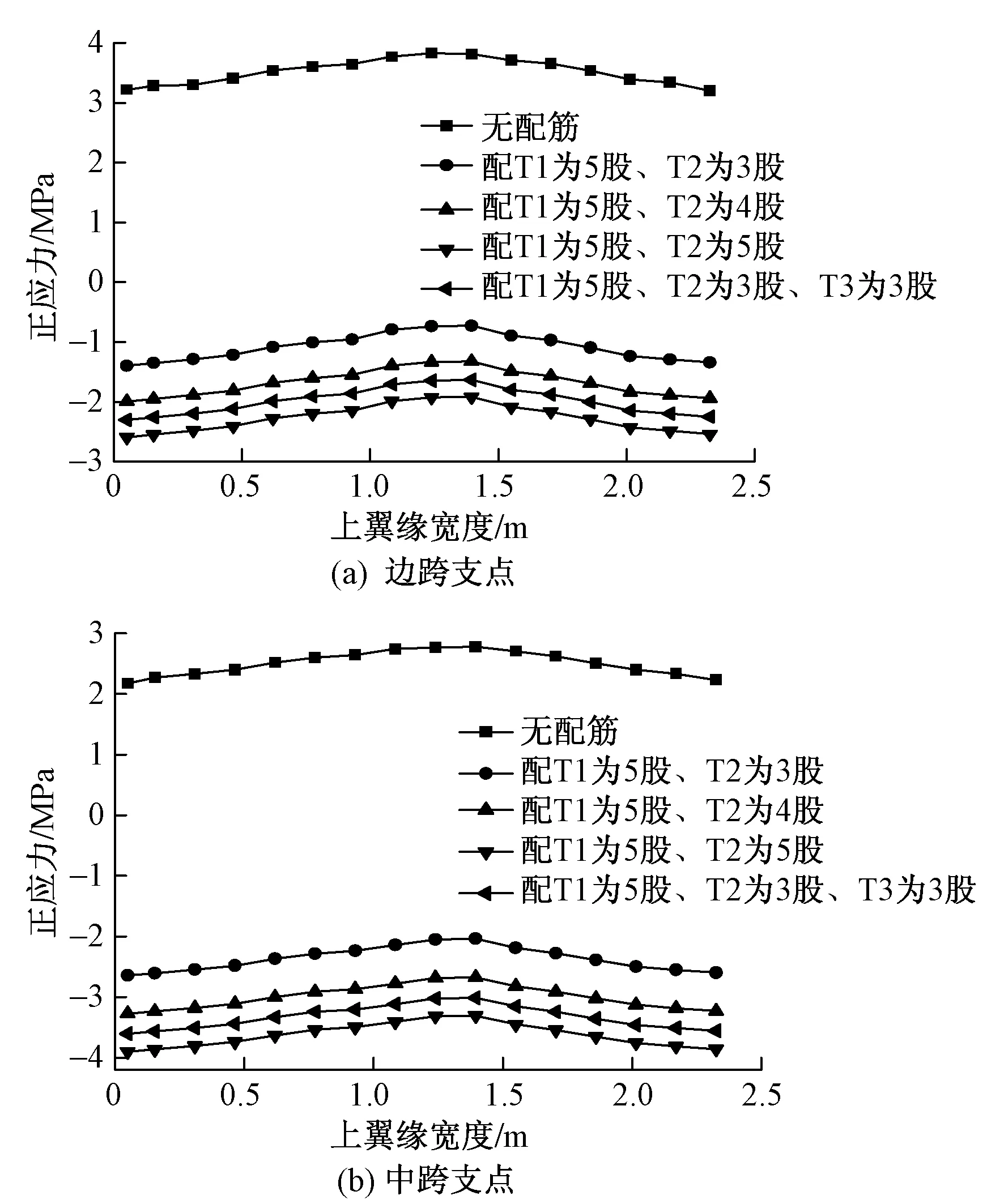
图4 支点上翼缘正应力分布
将配有不同布置位置、不同股数的预应力混凝土梁的应力值列入表1、表2进行比较。
由图4、表1、表2可知:预应力钢束能够有效减小支点上翼缘的正应力值,减小幅值较大,但是通过改变预应力钢束横向布置位置和股数基本无法改变整体混凝土梁的受力。另外应力极大值与极小值差值在配置预应力钢束后基本没有改变,其值约为0.6 MPa,支点由正剪力滞变为负剪力滞。因此,配置预应力钢束对于剪力滞效应基本没有影响。在理论上考虑剪力滞的翼缘板正应力公式为

表1 预应力混凝土在支点上翼缘正应力峰值

表2 荷载作用下的上翼缘支点处正应力极大值与极小值差值比较
(1)
(2)
(3)
式中:σx为弯曲正应力;u(x,y)为梁的纵向位移;u(x)为翼缘板剪切转角的最大差值;n,k为瑞斯纳函数;M(x)为弯矩;Q(x)为剪力;G为剪切模量;E为混凝土弹性模量;hi为翼缘板中心到截面形心距离;b为翼缘板宽度;I为全截面抗弯刚度;Is为翼缘板抗弯刚度;C1,C2为与边界条件相关的系数
式(1)括号中第一项为初等梁理论计算截面正应力的结果,第二项为考虑剪力滞效应的正应力值,与翼缘板最大剪切转角差值的导数有关。在式(2)中C1,C2只与边界条件有关而与荷载形式无关,第三项与梁体所受剪力有关,而配置在顶板处的预应力钢束为平行于翼板的直线钢束,只产生轴向力与弯矩,不会产生剪力,所以对于截面正应力分布不会产生影响。
配置预应力钢束使支点处的拉应力变为压应力,可以充分发挥混凝土的抗压强度,能够有效地避免上翼缘混凝土出现裂缝。本例分析对象为先简支后结构连续梁,对于连续梁,因为自重效应更需要防止中支点梁顶出现拉应力。
3 结论
1)对于装配式宽幅连续T梁桥,在支点翼缘板处剪力滞效应较为明显,在跨中和1/4跨径处剪力滞效应不明显。
2)配不同直径的普通钢筋或改变预应力钢束横向布置位置、钢束股数只能减小应力峰值,但应力峰值差基本不变,配普通钢筋和预应力钢束均无法抵消剪力滞效应。因此,剪力滞效应不受配普通钢筋或预应力钢束的影响,只与几何本身性质有关。
3)配置预应力钢束可大幅减小支点应力值,使支点处的拉应力变为压应力,可充分发挥混凝土的抗压强度,因此,配预应力钢束是防止支座顶部梁体出现裂缝的有效方法。在本例中剪力滞的应力峰值差约为0.6 MPa,因此配预应力钢束时需要预留>0.6 MPa的安全储备。对于连续梁,因为自重效应更需要注意支点顶部拉应力,注意预留更多的安全储备。
[1]周朋,蔺鹏臻.有限梁段法在箱梁施工阶段剪力滞分析中的应用[J].铁道建筑,2017,57(7):47-51.
[2]何志刚,刘应龙,周朋,等.混凝土箱梁开裂的剪力滞效应分析[J].铁道建筑,2017,57(9):25-30.
[3]蔺鹏臻,刘凤奎,杨军,等.箱梁剪力滞翘曲位移函数的定义及其应用 [J].计算力学学报,2012,29(5):789-794.
[4] 蔺鹏臻,周世军.基于剪切变形规律的箱梁剪力滞效应研究 [J ].铁道学报,2011,33(4):100-104.
[5] 罗旗帜.薄壁箱形梁剪力滞计算的梁段有限元法[J].湖南大学学报,1991,18(2):33-38,55.
[6] 吴幼明,罗旗帜,岳珠峰,等.薄壁箱梁剪力滞实验与计算研究 [ J ].公路交通科技,2004,21(2):73-76.
[7] 张元海,李琳,林丽霞,等.以附加挠度作为广义位移时薄壁箱梁剪力滞效应的梁段有限元分析[J].土木工程学报,2013,46(10):100-107.
[8]张元海,胡玉茹,林丽霞.基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J].土木工程学报,2015,48(6):44-50.
[9] 肖军,李小珍,刘德军,等.不同位移函数对箱梁剪力滞效应的影响[J].中国公路学报,2016,29(9):90-96.
[10] 蔺鹏臻,方炜彬,扬子江,等.预应力作用下箱梁桥的剪力滞效应研究[J].中国公路学报,2015,28(5):101-107.
[11] 蔺鹏臻,刘应龙,孙理想,等.预应力作用下简支箱梁桥的剪力滞效应分析[J].铁道工程学报,2014,31(11):54-58.
[12] 余天庆,宁柳明.悬臂预应力箱梁的剪力滞效应有限元分析 [J].湖北工业大学学报,2010,25(2):86-88.
[13] 刘君宏.预应力连续刚构桥剪力滞效应的研究[D].西安:长安大学,2011.
[14]朱明坤.预应力混凝土箱梁的剪力滞效应研究 [D].湖南:湖南大学,2013.
[15] 骆佐龙,宋一凡,贺栓海,等.薄壁箱梁剪力滞效应分析的组合单元法 [J].公路交通科技,2014,31(9):58-63.
