PEL负载模拟部分建模与仿真

童 炎， 廖冬初,2， 蔡华锋,2， 梅继超， 潘 健

(1. 湖北工业大学 电气与电子工程学院， 湖北 武汉 430068；2. 湖北工业大学 太阳能高效利用湖北省协同创新中心， 湖北 武汉 430068；3. 武汉征原电气有限公司， 湖北 武汉 430012)

0 引 言

交流能馈型直流电力电子负载是用于测试直流电源的一种装置， 能够将测试后剩余的电能回馈到电网， 不仅能够实现电源测试的自动化， 且相较于能耗型负载， 特别是大功率电力电子负载， 能够极大地节约电能， 因此其具有广阔的应用前景.

一般直流电力电子负载的主电路拓扑采用两级结构， 前级采用DC/DC变换器作为负载模拟部分， 后级则采用DC/AC变换器将电能回馈至电网. 其中DC/DC变换器多采用Boost电路[1-2]或者PWM整流器[3-5]， 因其不具有电气隔离的作用， 故后级逆变器通常需要经过工频变压器并网. 考虑到工频变压器不仅体积大， 而且存在一定的损耗， 故文献[6]和文献[7]的主电路拓扑采用三级结构， 均在Boost电路和DC/AC变换器之间加入一级移相全桥(Phase-Shifted Full-Bridge， PSFB)电路以实现电气隔离. 但因其结构复杂， 效率较低， 所以文献[8]和文献[9]仍采用两级结构. 文献[8]的前级直接采用移相全桥电路， 后级则采用逆变电路， 但其控制的是移相全桥的输出电流来实现负载模拟的功能， 其输入电流断续， 无法模拟输入电流连续恒流的特性. 而文献[9]的测试对象是电流源， 它是控制输入电压来实现负载模拟的功能. 本文研究的直流电力电子负载的测试对象是电压源， 同样采用两级结构， 但与文献[8]和文献[9]不同的是， 前级采用LC滤波电路和移相全桥电路级联作为负载模拟部分. 该部分的LC滤波电路能够保证输入电流连续， 为使控制简便， 对输入电流采用单环控制的方式， 但该部分为四阶电路， 因目前对其研究较少， 所以本文着重对该部分进行研究， 基于已有的PSFB电路的小信号模型[10-13]， 建立负载模拟部分的四阶模型， 再设计合适的PID控制器， 令其达到满意的控制效果.

1 主电路拓扑结构

本文研究的直流电力电子负载的主电路拓扑结构如图 1 所示.

图 1 直流电力电子负载的主电路拓扑结构Fig.1 Main circuit topology of DC PEL

前级采用LC滤波电路和移相全桥电路级联作为负载模拟部分， 后级采用LCL型逆变电路作为能量回馈部分， 两级之间使用容值为10 200 μF的大电容连接， 以便实现解耦控制. 前级负责对输入电流进行单环控制实现负载模拟的功能， 后级则以中间直流母线电压为外环， 并网电流为内环进行控制， 将能量回馈到电网.

2 负载模拟部分的模型分析

负载模拟部分与输入电流为被控对象， 采用单环控制， 控制框图如图 2 所示.

图 2 负载模拟部分的控制框图Fig.2 Control block diagram of load simulation part

从控制框图可以看出， 输入电流对占空比的传递函数是分析系统行为以及设计调节器的基础. 虽然已有PSFB电路的小信号模型， 但并不能直接得到输入电流对占空比的传递函数， 因此有必要在PSFB电路小信号模型的基础上， 先建立负载模拟部分的小信号模型， 再进行分析和设计.

负载模拟部分的拓扑结构如图 3 所示， 被测电源的输出电压为Vg， 输入电感L的作用是使输入电流连续且纹波较小， 输入电容C则是令PSFB电路的输入电压基本保持不变，Lr为谐振电感，Cb为谐振电容，Lf和Cf分别为PSFB电路中的输出滤波电感和滤波电容， 高频变压器T的原副边匝比为n，R为等效负载.

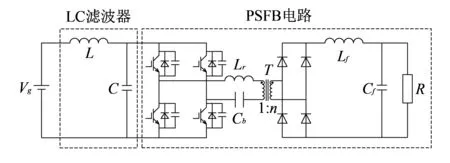
图 3 负载模拟部分的拓扑结构Fig.3 Topology of load simulation part

PSFB电路属于Buck型变换器， 由于存在占空比丢失的现象， 需要在Buck变换器的小信号模型的基础上加以改进. 有效占空比Deff的表达式为

Deff=D-ΔD,

(1)

式中：D为控制器输出的占空比； ΔD是丢失占空比， 其表达式为

(2)

式中：n是变压器原副边匝比；Vc是PSFB的输入电压；Ts是开关周期；Vo是输出电压；ILf是电感Lf的电流.

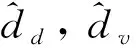
(3)

式中：Rd=4n2Lrfs，fs是开关频率.

将以上三种扰动加入Buck变换器的小信号模型中即可得到较为精确的PSFB电路的小信号模型， 如图 4 所示.

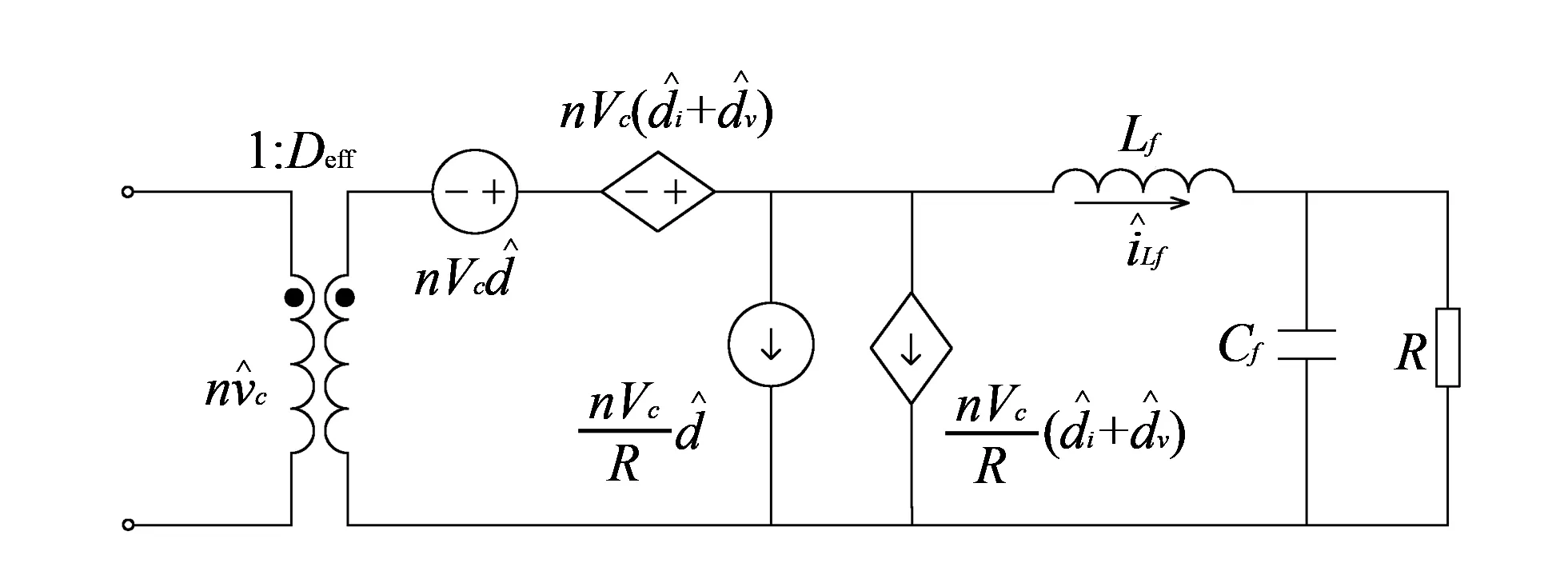
图 4 PSFB电路的小信号模型Fig.4 Small signal model of PSFB circuit

在PSFB电路的小信号模型的基础上加入LC滤波电路， 得到负载模拟部分的小信号模型如图 5 所示.

图 5 负载模拟部分的小信号模型Fig.5 Small signal model of load simulation part

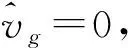
可得输入电流i对占空比d的传递函数为

(4)

式中：

K=n2DeffRVg,

a0=2R,

a1=R2Cf+Lf,

a2=RCfLf,

b0=R2Rd+R3,

b2=R3CL+R3CfLf+R2RdCL+

b4=R3CLCfLf.

3 负载模拟部分的控制

本文所研究的电力电子负载的额定功率为70 kW， 额定输入电压为600 V， 如图 3 所示， 输入电感L的值为1.5 mH， 输入电容C的值为5 600 μF， 输出滤波电感Lf的值为800 μH， 输出滤波电容Cf的值为10 200 μF， 谐振电感Lr的值为12 μH， 隔直电容Cb的容值为120 μF， 开关频率fs为8 kHz， 高频变压器T的原副边的匝比n为1.5. 从输入电流对占空比的传递函数可以看出， 传递函数与有效占空比Deff和等效负载R的值有关.

显然， 系统动态调节过程中， 有效占空比Deff会发生变化. 假设系统工作过程中效率η保持不变， 则有ηVgI=VoIo， 输入电压Vg由被测电源提供， 被测电源是一个恒压源， 在电子负载运行过程中其输出电压一直保持不变； 输出电压Vo即输出滤波电容Cf的电压， 它由后级逆变器控制稳定在600 V， 同样基本保持不变； 因此当改变输入电流I的给定即改变负载模拟的大小时， 输出电流Io会随之改变. 同时， 由R=Vo/Io可知， 移相全桥的等效负载R也会发生变化.

在系统运行过程中， 有效占空比Deff和等效负载R的值不是固定不变的， 为了使设计的控制器具有很好的鲁棒性， 必须保证系统在条件最坏的情形下都能正常工作. 假设系统动态调节过程中Deff的变化范围是0.1～0.9； 当系统工作在10%～100%的额定功率时， 假设系统效率η=1， 则等效负载R的取值范围是5.14～51.4 Ω. 先分别求出: ①Deff=0.1，R=5.14； ②Deff=0.1，R=51.4； ③Deff=0.9，R=5.14； ④Deff=0.9，R=51.4四种极限情形下的传递函数， 分别为G1(s),G2(s),G3(s),G4(s)， 使用MATLAB软件， 画出这四个传递函数的Bode图， 观察和比较这四种情况的Bode图， 找出最坏的情况， 根据最坏的情况的传递函数对系统进行校正， 设计出合适的PID控制器. 这四种情况的Bode图如图 6 所示.

图 6 四个开环传递函数的Bode图Fig.6 The Bode diagram of four open loop transfer functions

对比图 6 的(a)和(b)可知， 以上四种情况的相位裕度均小于0°， 而G4(s)的相位裕度最小， 稳定性最差， 因此只要设计的调节器能保证系统在第四种情况下可稳定工作， 那么系统在其他情况下也能正常工作.

对于一般的系统， 控制器采用PI调节器即可， 但是对于本系统， 仅采用PI调节器不能使系统稳定工作， 需要加入一个微分环节使系统的相位裕度增加， 另外， 为了不影响系统对高频信号的衰减， 并减弱微分环节对干扰的敏感度， 因此采用不完全微分的PID调节器， 其传递函数的一般形式为

(5)

选取7组PID参数， 对G4(s)进行校正后， 系统相应的相位裕度和穿越频率如表 1 所示. 对比第1, 2, 3组数据可知， 比例系数Kp越大， 相位裕度越小， 但穿越频率越大； 对比第2, 4, 5组数据可知， 积分时间常数TI几乎对相位裕度和穿越频率没有影响， 对比第2, 6, 7组数据可知， 微分时间常数Td越大， 相位裕度越小， 但穿越频率越大. 相位裕度关系着系统的稳定性， 而穿越频率越大， 系统的响应速度越快， 为了兼顾系统的动态性能和稳态性能， 选择第2组参数作为控制器参数： 比例系数Kp=0.01， 积分时间常数TI=1/100， 微分时间常数Td=1/150， 小惯性环节的时间常数Tf=0.000 01.

表 1 PID参数对系统性能的影响Tab.1 Effect of PID parameters on system performance

加入校正环节后， 系统的Bode图如图 7 所示.

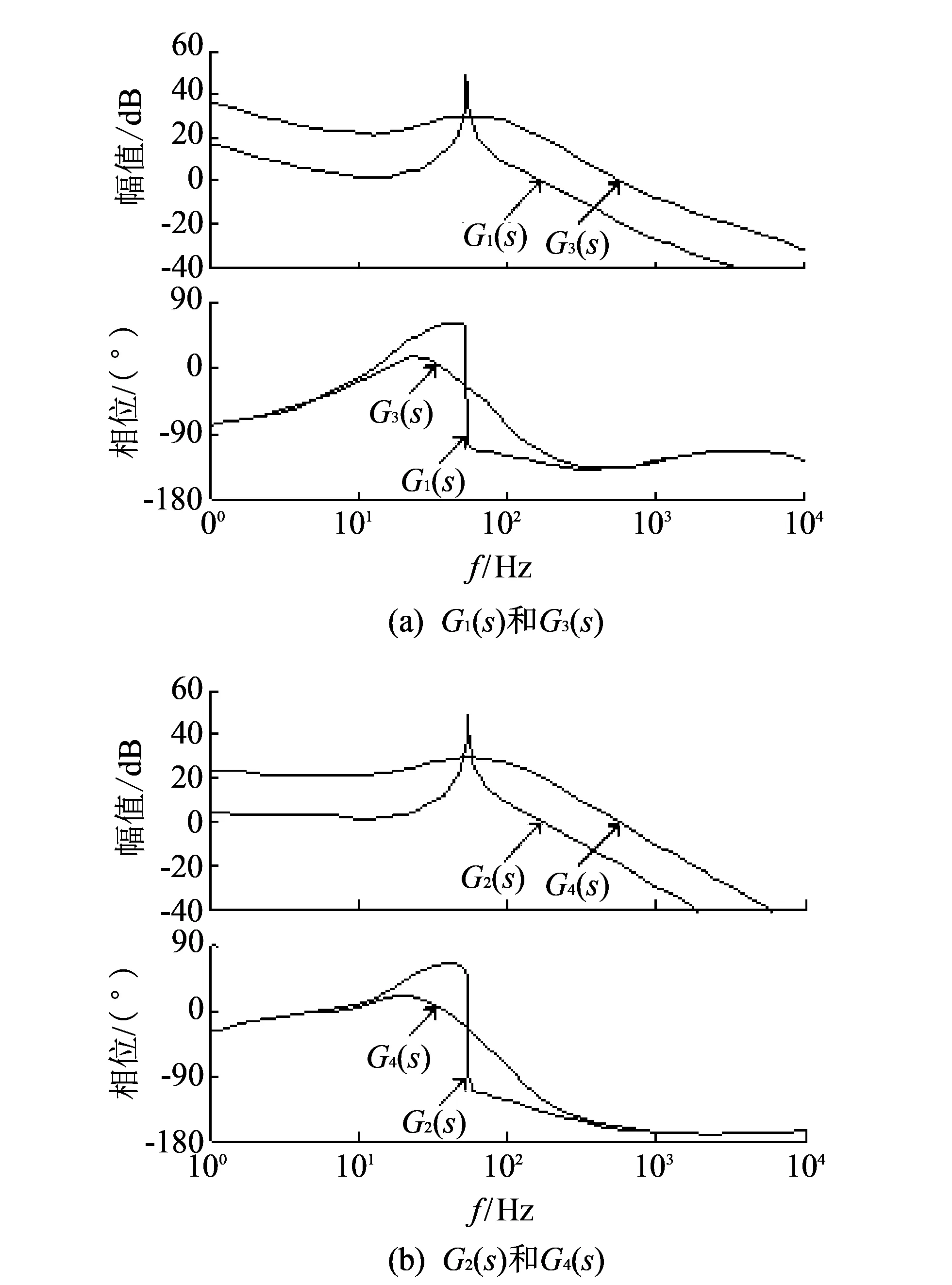
图 7 校正后系统的Bode图Fig.7 The Bode diagram of the corrected system

因为电力电子负载稳定工作时， 后级逆变器的电压外环会将中间直流母线电压即PSFB电路的输出电压Vo始终稳定在600 V， 而输入电压Vg为600 V， 变压器匝比n为1.5， 根据Vo=nDVg可知， 系统稳定工作时， PSFB电路的占空比D基本保持在0.67左右. 虽然系统加入校正环节后， 由图 7 可知，G4(s)的相位裕度虽然只有16.6°， 但这种工作情况只会在负载突增和负载突减的情况下短暂出现， 而其他三种情况下， 系统的相位裕度均在40°以上， 所以设计的PID控制器能使系统稳定工作.

4 系统仿真验证

基于MATLAB搭建负载模拟部分的仿真模型， 模型中的主电路参数和控制器中的PID调节器参数均按第3节的参数进行设置， 对系统在轻载和满载两种情况下的工作状况进行分析.

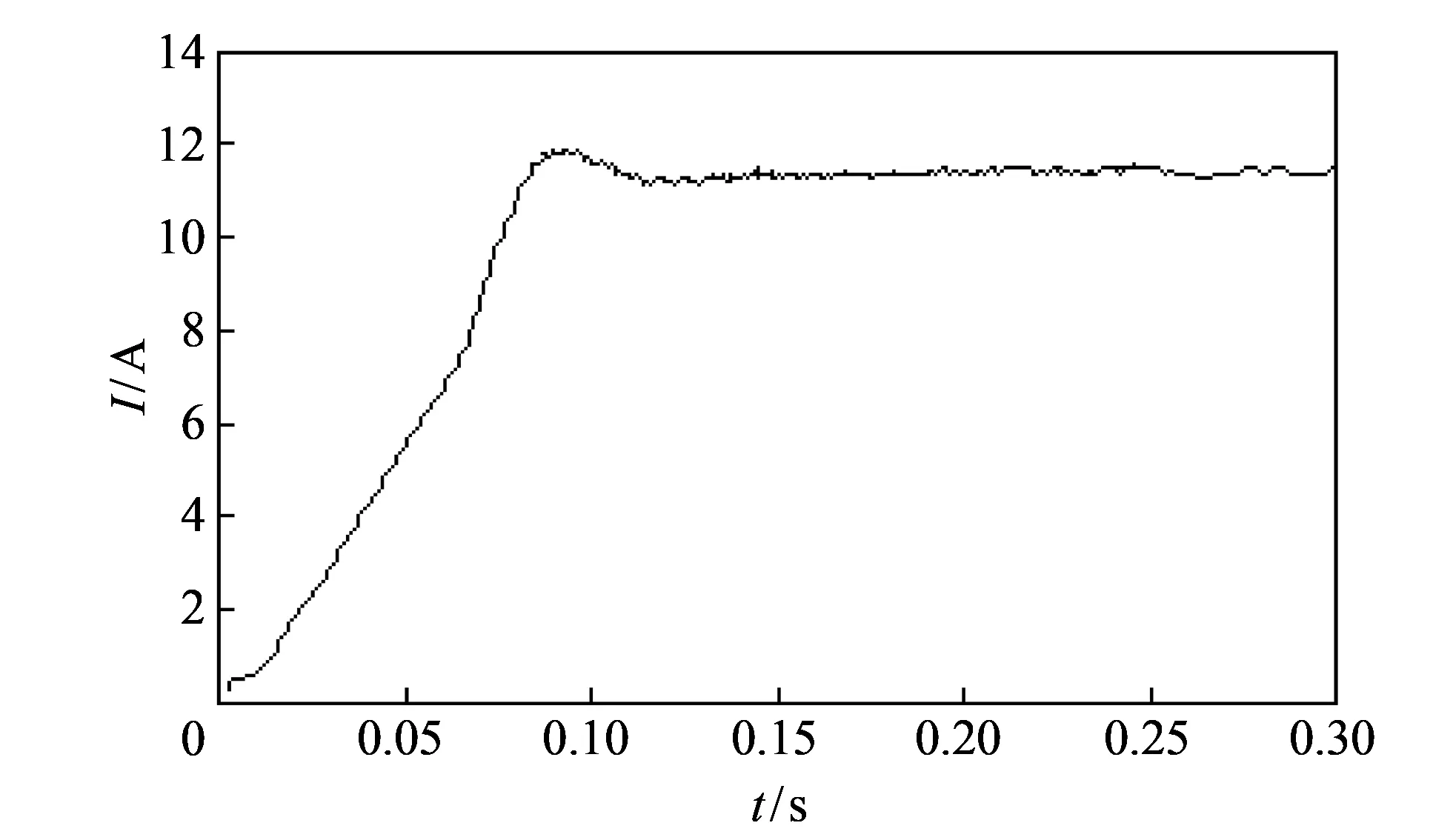
图 8 轻载时的输入电流的波形Fig.8 Waveform of the input current in light load

当电力电子负载工作在100%的额定功率下时， 输入电流I的给定值应设置为116.7 A， 等效负载R应设置为5.14 Ω， 此时输入电流I的波形如图 9 所示.

由图 8 和图 9 可知， 系统在轻载和满载的情况下， 均能稳定工作. 在轻载的情况下， 输入电流的响应时间大约为120 ms， 而满载情况下， 输入电流的响应时间大约为50 ms， 可以看出负载越大， 输入电流的响应越快.

图 9 满载时的输入电流的波形Fig.9 Waveform of the input current at full load

在负载模拟部分的仿真模型基础上加入LCL型逆变器的仿真模型， 搭建出完整的电力电子负载仿真模型， 如图 1 所示， 逆变器的逆变侧电感L1为400 μH， 并网侧电感L2为200 μH， 电容Cc为40 μF， 并网电压为AC380V.

当t=0.25 s时， 给定输入电流I从58.3 A突增到116.7 A时的输入电流I波形， 如图 10 所示.

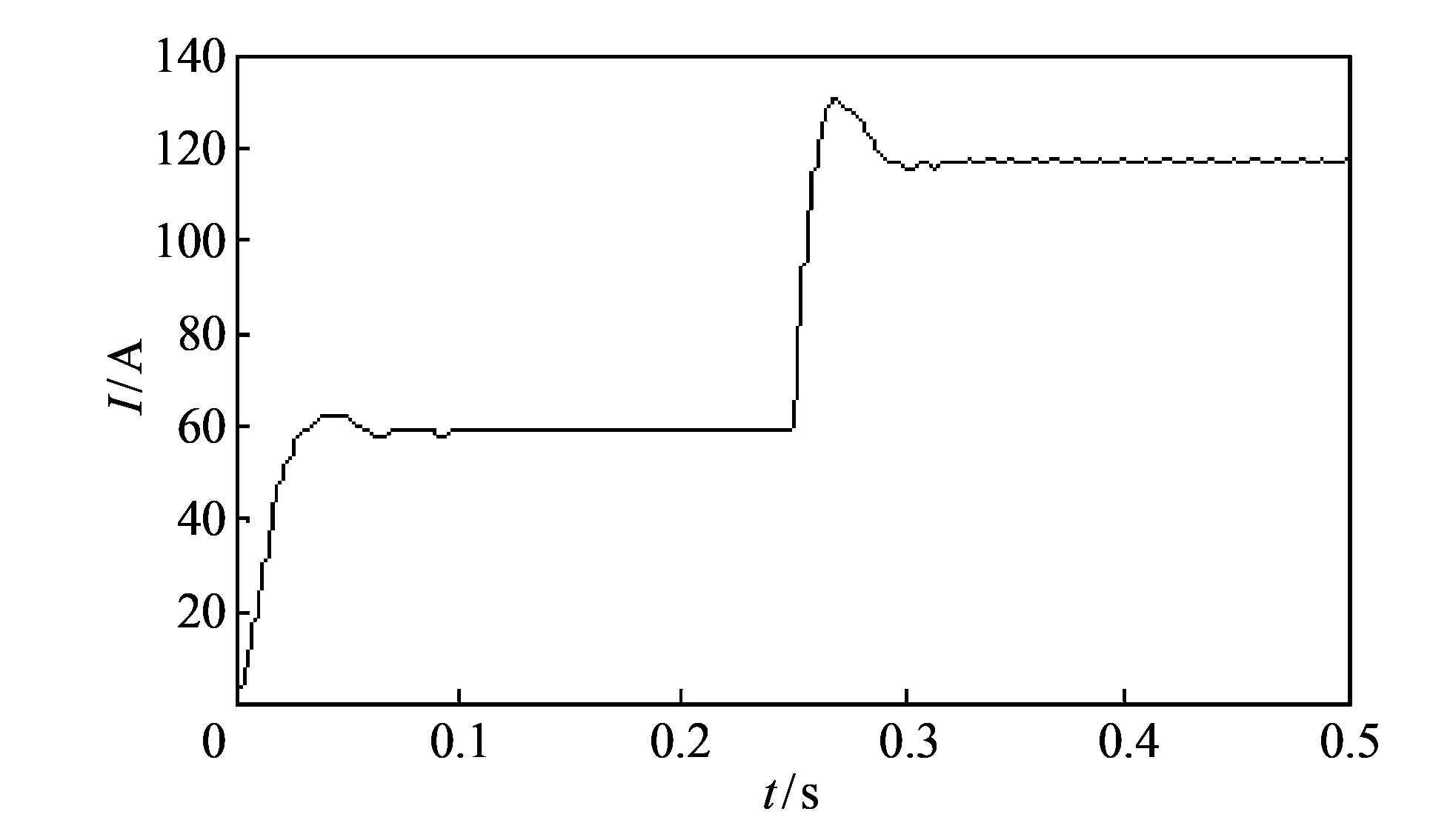
图 10 负载突增的输入电流波形Fig.10 Input current waveform with sudden increased load

当t=0.25 s时， 给定输入电流I从116.7 A突减到58.3 A时的输入电流I波形， 如图 11 所示.

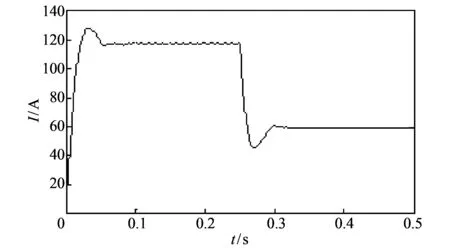
图 11 负载突减的输入电流波形Fig.11 Input current waveform with sudden reduced load

由图 10 和图 11 可知， 前后两级同时工作时， 无论是负载突增还是突减的情况下， 系统均能稳定工作， 输入电流的响应时间较快， 大约50ms就再次达到稳定状态.

5 结 论

针对所提出的电力电子负载的结构， 建立了负载模拟部分的小信号模型， 并推导出输入电流对占空比的传递函数， 在此基础上， 设计出合适的PID控制器， 最后通过仿真实验证明了根据负载模拟部分的小信号模型所设计的PID控制器的控制效果良好， 同时说明所建立的负载模拟部分的小信号模型是合理的.

参考文献：

[1] 刘美茵. 电能回馈型电子负载的研究与实现[D]. 哈尔滨： 哈尔滨工业大学， 2010.

[2] 王成， 廖冬初， 蔡华锋. 直流回馈型直流电子负载的设计与研究[J]. 电测与仪表， 2017， 54(6)： 23-29.

Wang Cheng, Liao Dongchu, Cai Huafeng. Design and research of DC feedback type of DC electronic load[J]. Electrical Measurement & Instrumentation, 2017, 54(6)： 23-29. (in Chinese)

[3] 黄朝霞， 邹云屏， 王成智. 基于PI控制的电力电子负载[J]. 高电压技术， 2009， 35(6)： 1451-1456.

Huang Zhaoxia, Zou Yunping, Wang Chengzhi. Power electronic load based on PI control[J]. High Voltage Engineering, 2009, 35(6)： 1451-1456. (in Chinese)

[4] 齐焱. 单相能馈式电力电子负载的研究[D]. 哈尔滨： 哈尔滨理工大学， 2015.

[5] 强金星. 基于400 Hz逆变器的单相电力电子负载系统研究[D]. 武汉： 华中科技大学， 2012.

[6] 徐勇. 高升压比能量回馈型直流电子负载的设计与实现[D]. 成都： 电子科技大学， 2013.

[7] 陈强， 鞠文耀， 贾中璐. 电能回馈直流电子负载的设计与实现[J]. 电力电子技术， 2011， 45(7)： 108-110.

Chen Qiang, Ju Wenyao, Jia Zhonglu. Design and realization of energy feedback type DC electronic load[J]. Power Electronics, 2011, 45(7)： 108-110. (in Chinese)

[8] 郑连清， 王青峰. 馈能型电子负载的并网控制[J]. 电网技术， 2008， 32(7)： 40-45.

Zheng Lianqing, Wang Qingfeng. Grid-connected control of feedback type electronic load[J]. Power System Technology, 2008, 32(7)： 40-45. (in Chinese)

[9] 张胜高. 基于移相全桥的馈能式直流电子负载设计[D]．济南： 山东大学， 2013.

[10] 林荫宇， 张金奎， 刘洋溢， 等. 移相全桥零电压PWM变换器的建模与仿真[J]. 重庆大学学报(自然科学版)， 2000， 23(2)： 49-52.

Lin Yinyu, Zhang Jinkui, Liu Yangyi, et al. Full bridge zero-voltage-switched PWM converter[J]. Journal of Chongqing University (Natural Science Edition), 2000, 23(2)： 49-52. (in Chinese)

[11] 王海莉， 吴延华. 移相全桥变换器的建模与仿真[J]. 通信电源技术， 2008， 25(5)： 41-42.

Wang Haili， Wu Yanhua. Modeling and simulation of FB ZVS-PWM converter[J]. Telecom Power Technolgies, 2008, 25(5)： 41-42. (in Chinese)

[12] Hu Xuezhi, Nan Guangqun. The research of modeling and simulation for phase-shifted full-bridge ZVS DC/DC converter[J]. Third International Symposium on Intelligent Information Technology Application, 2009(2)： 549-552.

[13] 张卫平. 开关变换器的建模与控制[M]. 北京： 中国电力出版社， 2005.

[14] 阮新波. 脉宽调制DC/DC全桥变换器的软开关技术[M]. 第2版. 北京： 科学出版社， 2013.

[15] 阮新波， 王学华， 潘冬华， 等. LCL型并网逆变器的控制技术[M]. 北京： 科学出版社， 2015.