一类耦合的Euler-Bernoulli梁的渐近稳定性
2018-06-04赵转萍
赵转萍
(山西大学商务学院 基础教学部, 山西 太原 030031)
0 引 言
梁方程是一种双曲方程, 是偏微分方程的重要研究内容之一. 在控制领域, 各式各样的动态反馈产生了大量的含有梁方程的耦合系统[1-2]. 因此, 耦合的梁方程的研究逐渐得到了人们的重视[3]. 与上述文献不同, 本文考虑Euler-Bernoulli梁和抽象系统组成的耦合系统.
首先在有界区间上考虑如下Euler-Bernoulli梁的控制问题:梁的一端是简支的, 另一端有一个动态反馈
(1)
式中:G是 Hilbert 空间上的自伴的严格正算子;z*∈Z是任意给定的非零元素; (w0,w1,z0)是初始状态;w表示振动的梁的位移;z表示抽象的动态控制变量. 容易看出, 不同的空间Z和不同的算子G将产生不同的耦合系统. 当G是n阶正定矩阵时, 系统(1)变成声学结构模型[4-6], 当G是微分算子G=-∂xx时, 系统(1)成为一个梁-热耦合系统[7]. 系统(1)主要考虑线性动态反馈, 因此与文献[8]考虑的问题不同.
在状态空间(2)中考虑系统(1),
(2)
其中,H=L2(0,1), 且
f′(0)=0}.
(3)
系统(1)的能量函数为

(4)
对能量函数求导可得
(5)
由于等式(5)右端没有w的任何信息, 因此用传统的李雅普诺夫函数分析方法来证明系统的稳定性将会变得非常困难. 受文献[9]的启发, 本文将从控制的角度来考虑系统解的适定性和渐近稳定性, 这为偏微分方程的稳定性分析提供了一个新思路.
1 适定性和渐近稳定性
近年来, 有很多文献在研究耦合系统解的适定性和渐近稳定性, 例如[10]和 [11], 然而这些研究大多是基于偏微分方程的方法. 与此不同, 本文将从控制的角度来考虑系统解的适定性和渐近稳定性. 首先, 将耦合系统(1)分解成两部分:控制系统和动态反馈系统. 事实上, 耦合系统(1) 恰好是控制系统
(6)
动态反馈下的闭环系统
u(t)=〈z(t),z*〉Z,
(7)
其中,z满足
(8)
定义算子A∶D(A)⊂L2(0,1)→L2(0,1)为
(9)
其中,A是H=L2(0,1)上的严格正定的自伴算子[12], 并且有如下Gelfand三嵌入
D(A1/2)→H→D(A1/2)′,
(10)

〈A1/2x,A1/2y〉H,∀x,y∈D(A1/2),
(11)
所以, 系统(6)可以写成抽象系统
(12)
Bu=uδ(x-1), ∀u∈U=C,
(13)
这里δ(·)为Dirac分布. 如果定义B的共轭算子B*∈L(D(A1/2),U)为
〈B*z,u〉U=〈z,Bu〉D(A1/2),D(A1/2)′,
∀z∈D(A1/2),u∈U,
(14)
则直接计算可得
B*f=f(1), ∀f∈D(A1/2).
(15)
令F∈L(Z,U)满足
Fz=-〈z,z*〉Z, ∀z∈Z,
(16)
则对任意的u∈U,F*∈L(U,Z)满足F*u=-uz*. 由于z*≠0, 因此
KerF*={0}.
(17)
借助于上面定义的算子, 方程(7)和(8)可以写成
u(t)=-Fz(t)
(18)
和
(19)
所以, 将系统(1)写成了如下抽象系统
(20)
其中,C=BF∈L(D(G1/2),D(A1/2)′),C*=F*B*∈L(D(A1/2),D(G1/2)′) 满足
anomalies over the western Pacific Ocean warm pool and its possible mechanism
〈C*g,z〉Z=〈B*g,Fz〉U=〈g,Cz〉D(A1/2),D(A1/2)′,
∀g∈D(A1/2),z∈Z.
(21)
在状态空间H中考虑抽象系统(20). 如果定义A∶D(A)(⊂H)→H为

(22)
则系统(20)进一步可写成H中的发展方程
(23)
定理1 设G是Hilbert空间Z上自伴的、 严格正的算子, 0≠z*∈Z. 如果G-1在Z是紧的, 则对任意的(w(·,t),wt(·,0),z(0))∈H, 系统(1)在H上存在唯一的C0-半群解. 此外, 该解是渐近稳定的
‖w(·,t),wt(·,t),z(t)‖H→0, 当t→∞.
(24)
证明简单计算可知, 对任意的(f,g,z)∈D(A), 有
Re〈A(f,g,z),(f,g,z)〉H=
〈Cz,g〉D(A1/2)′,D(A1/2)-〈Gz,z〉Z-〈C*g,z〉Z]=

(25)
这说明算子A在H中是耗散的. 对任意的(φ,φ,ψ)∈H, 解方程A(f,g,z)=(φ,φ,ψ)∈H可得
(26)

φ,-G-1(F*B*φ+ψ)).
(27)
因此,A-1存在且在H上有界. 由 Lumer-Phillips 定理[13],A生成H上的C0-压缩半群.
为了证明系统(1)的渐近稳定性, 首先考虑
Ker(B*)∩Ker(λ-A)={0}, ∀λ>0,
(28)
式(28)等价于:对任意的λ>0, 特征方程(29)只有零解
(29)
直接计算可得: 式(29)只有零解是显然的, 从而式(28)成立.
另一方面, 由于G-1在Z中紧, 所以, 式(27)意味着A-1在H中紧. 因此, 由文献 [14]可知, 只需证明算子A在虚轴上没有谱点即可. 事实上, 如果设A(f,g,z)=iω(f,g,z), (f,g,z)∈D(A)且0≠ω∈R. 则
(30)
方程(30)等价于
(31)
方程(31)的第一个方程两边关于f取内积, 同时第二个方程两边关于iωz取内积可得
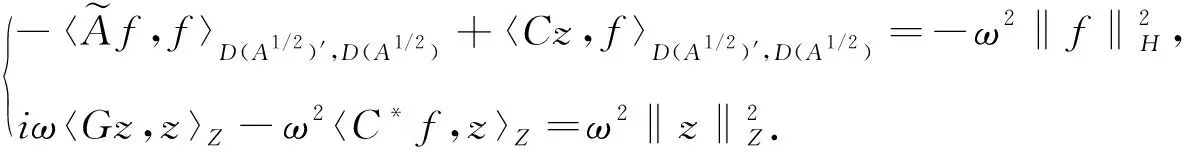
(32)
方程(32)的第一个方程乘以-ω2, 再加第二个方程可得
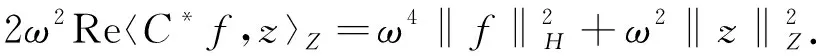
(33)

2 应用举例
由于系统(1)由算子G和Hilbert空间Z决定, 不同的G和Z意味着不同的耦合系统. 下面给出具体的例子来说明这一问题.
例1 如果令G=1,Z=R且z*=1, 则抽象系统(1)变为
(34)
简单计算可知, 上面定义的G和Z满足定理1的所有条件, 因此系统(34)是渐近稳定的. 特别地, 系统(34)对应的半群解为eA1t(w(·,0),wt(·,0),z(0)), 其中系统算子A1定义为
(35)
系统(34)的边界条件称为声学边界条件. 类似问题可查阅文献[15].
例2 令Z=L2(0,1),x∈Z, 定义算子G∶D(G)⊂Z→Z为Gf=-f″, 其中f∈D(G)={f∈H2(0,1)|f(0)=f′(1)=0}, 则系统(1)变为
(36)
与例1类似, 简单计算可知, 上面定义的G是Hilbert空间Z上自伴的、 严格正的算子, 满足定理1的所有条件, 所以系统(36)是渐进稳定的. 此外, 系统(36)对应的半群解为eA2t(w(·,0),wt(·,0),z(0)), 其中系统算子A2定义为
(37)
参考文献:
[1] Wei Guo, Chen Yunlan, Feng Hongyinping. Output feedback stabilization for a Kirchhoff-type nonlinear beam with general corrupted boundary observation[J]. Int. J. Robust Nonlinear Control, 2017, 27(16): 3280-3295.
[2] Zhou Huachen, Feng Hongyinping. Disturbance estimator based output feedback exponential stabilization for Euler-Bernoulli beam equation with boundary control[J]. Automatica, 2018, 91(5): 79-88.
[3] Mercier D, Nicaise S, Sammoury M et al. Optimal energy decay rate for rayleigh beam equation with only one dynamic boundary control[J]. Bol. Soc. Paran. Mat, 2017, 35(3): 131-171.
[4] Abbas Z, Nicaise S. Polynomial decay rate for a wave equation with general acoustic boundary feedback laws[J]. SeMA Journal, 2013, 61(1): 19-47.
[5] Abbas Z, Nicaise S. The multidimensional wave equation with generalized acoustic boundary conditions II: strong stability[J]. SIAM J. Control Optim, 2015, 53(4): 2582-2607.
[6] Abbas Z, Nicaise S. The multidimensional wave equation with generalized acoustic boundary conditions I: strong stability[J]. SIAM J. Control Optim, 2015, 53(4): 2558-2581.
[7] Zhang Qiong, Wang Junmin, Guo Baozhu. Stabilization of the Euler-Bernoulli equation via boundary connection with heat equation[J]. Math. Control Signals Syst, 2014, 26(1): 77-118.
[8] Le Gorrec Y, Zwart H, Ramirez H. Asymptotic stability of an Euler-Bernoulli beam coupled to non-linear spring-damper systems[J]. IFAC-papersonline, 2017, 50(1): 5580-5585.
[9] Feng Hongyinping, Guo Baozhu. On stability equivalence between dynamic output feedback and static output feedback for a class of second order in_nite-dimensional systems[J]. SIAM J. on Control and Optimization, 2015, 53(4): 1934-1955.
[10] Feng Hongyinping, Li Shengjia. The stability for a one-dimensional wave equation with nonlinear uncertainty on the boundary[J]. Nonlinear Anal, 2013, 89(6): 202-207.
[11] Vicente A, Frota C. On a mixed problem with a nonlinear acoustic boundary condition for a non-locally reacting boundaries[J]. Math. Anal. Appl, 2013, 407(2): 328-338.
[12] Tucsnak M, Weiss G. Observation and control for operator semigroups[M]. Basel: Birkhauser, 2009.
[13] Pazy A. Semigroups of linear operators and applications to partial differential equations[M]. New York: Springer-Verlag, 1983.
[14] Luo Zhenghua, Guo Baozhu, Morgul O. Stability and stabilization of infinite dimensional systems with applications[M]. London: Springer-Verlag, 1999.
[15] Wehbe A. Rational energy decay rate for a wave equation with dynamical control[J]. Appl. Math. Lett, 2003, 16(3): 357-364.
