RN上临界p-Kirchhoff型方程非平凡解的存在性
2018-06-04刘进生
王 萍, 刘进生
(太原理工大学 数学学院, 山西 太原 030024)
本文主要利用变分方法, 结合山路引理与集中紧性原理, 研究了RN上带有临界非线性项的p-Kirchhoff型问题
RN上的Kirchhoff型问题
(1)
作为椭圆型方程非局部问题的典型代表, 并且它又在实际生活中被广泛应用, 故而近年来有许多作者研究了其非平凡解的存在性[1-7]. 与此同时, 也有大量作者将问题(2)推广到含有p-Laplace算子Δp的情形, 即所谓的p-Kirchhoff 型问题, 如文献[8-12]研究了p-Kirchhoff问题
(2)
非平凡解的存在性. 文献[13]又研究了更一般的p-Kirchhoff型问题
(3)
非平凡解的存在性与多重性. 但文献[13]的研究方法不适合问题(P)的研究, 因为问题(3)中的非线性项f是次临界的, 而我们所研究的问题(P)中的非线性项含有临界项|u|p*-2u.
本文所使用的方法是文献[6]与[7]研究方法的一个结合与推广. 主要结论为
定理1 假设p2 1)p2 对任意的1≤s≤+∞,|·|s表示通常的Lebesgue 空间Ls(RN)上的范数. 对固定的常数a,m> 0, 可以在W1,p(RN)中引入等价范数, 即u∈W1,p(RN)时, 定义 可以证明, 当u∈W1,p(RN)时, 问题(P)所对应的能量泛函为 (4) 并且I∈C1W1,p(RN),R, 从而由式(4)定义的泛函I的临界点即为问题(P)在W1,p(RN)中的解. 本文中, 由于问题(P)是自治的,结合对称临界原理, 只需在径向对称空间 RN)= {u∈W1,p(RN)∶u(x)=u(|x|)} 中证明I存在非零的临界点即可. 引理1 当p2 证明显然有I(0)=0. 由式(4), 利用Bernoulli 不等式((1+x)α≥1+αx,α>1,x>-1)及Sobolev嵌入定理知, 存在常数C1,C2>0使得 注意到p 根据山路引理及引理 1, 令Γ是E中联结0与e的道路的集合, 即 Γ={g∈C([0,1],E)|g(0)=0,g(1)=e}, 记 (5) 那么c≥α并且I关于c存在临界序列{un}. 若I还满足(PS)c条件, 则c是I的临界值. 为了证明{un}在E中满足(PS)c条件, 需要给出式(5)中c的一个上界并证明{un}在E中是有界的. 记空间D1,p(RN)={u∈Lp*(RN)∶u∈Lp(RN)} 中的Sobolev最佳嵌入常数为S, 注意到p2 (6) 有唯一的正实根, 记为μ. 定义 (7) 那么, 由式(6)容易知道 引理2 若定理1的假设条件成立, 则c 证明对任意的ε,r>0, 取Uε(x)=φ(x)U(x,ε), 其中 直接计算有 (8) 且当p2≥N时, 有 (9) 当p2 (10) 那么 3) 当t′ 则 y′(t)= 由此容易证明y(t)存在唯一的最大值点tε>0, 它满足y′(t∈)=0. 令 注意到 结合式(8)可知, 当ε→0时, 所以, 由式(6)可得F(μ,A0,B0,C0)=0, 而 于是由隐函数定理可知, 在点(μ,A0,B0,C0)附近, 方程F(tε,Aε,Bε,Cε)=0可以确定隐函数 tε=f(Aε,Bε,Cε), 从而由隐函数的连续性知, 当ε→0时,tε→μ, 将其在点(A0,B0,C0) Taylor展开得到 tε=f(A0,B0,C0)+ (11) 于是将函数y(t)中的每一项都在t=μ点Taylor展开, 计算可得,y(tε)=c*+O(εα), 而当t′ 综合(1), (2)及(3)可知在定理1的假设条件下c 引理3 当p2 证明一方面, 因为当n→∞时,I(un)→c,I′(un)→0, 故 (12) 式中:εn→0(n→∞). 另一方面, 仍利用Bernoulli不等式, 容易估计出 (13) 注意到p>1, 故由式(12)及(13)知, {un}是有界的. 定理1的证明只需证明由式(4)定义的泛函I满足(PS)c条件. 假设{un}⊂E, 满足I(un)→c,I′(un)→0. 由引理3知{un}是有界的, 于是对{un}的某个子列, 仍记为{un}, 存在u∈E, 使得 (14) 由集中紧性原理[15], 结合空间E的特性知, 对{un}的某个子列, 仍记为{un}, 存在数η0,v0≥0使得在测度意义下有 |un|p⇀dη≥|u|p+η0δ0, |un|p*⇀dv=|u|p*+v0δ0, (15) 下面证明η0=v0=0. 用反证法. 若η0,v0中至少有一个不为零, 与文献[7]中的证明同理可得, 对固定的v0,η0, 有v0≥(a+bη0)p-1η0, 因此有 (16) 从而η0,v0>0, 再结合收敛性结论(14), 计算得到 (17) 对于函数 故 因此, 由式(17)得到c≥c*, 这与引理2的结论矛盾, 故η0=v0=0. 而由文献[16]可知 (18) 其中 因此 (19) 由I′(un)→0, {un}的有界性以及式(14)可得 o(1)=〈I′(un)-I′(u),un-u〉= (20) 由Hölder不等式, {un}的有界性以及式(19)可得 (21) 又因为un⇀u, 且{un}有界, 故可得 (22) 由文献[17]知存在正常数Cp, 使得对任意的ξ,η∈RN, 有 (23) 因此, 由式(23), Hölder不等式及{un}的有界性知, 存在正常数C使得 (24) 且 (25) 则由式(20)~(25)可得 所以 因此, ‖un-u‖→0, 结合在E中un⇀u, 可以得到在E中un→u. 参考文献: [1] He Xiaoming, Zou Wenming. Existence and concentration behavior of positive solutions for a Kirchhoff equation inR3[J]. Journal of Differential Equations, 2012, 252(2): 1813-1834. [2] Liu Zhisu, Guo Shangjiang. Positive solutions for asymptotically linear Schrödinger-Kirchhoff-type equations[J]. Mathematical Methods in the Applied Sciences, 2014, 37(4): 571-580. [3] Nie Jianjun. Existence and multiplicity of nontrivial solutions for a class of Schrödinger-Kirchhoff-type equations[J]. Journal of Mathematical Analysis and Applications, 2014, 417(417): 65-79. [4] Liu Zhisu, Guo Shangjiang. Existence of positive ground state solutions for Kirchhoff type problems[J]. Nonlinear Analysis: Theory, Methods and Applications, 2015, 120: 1-13. [5] Wu Yue, LiuShibo. Existence and multiplicity of solutions for asymptotically linear Schrödinger-Kirchhoff equations[J]. Nonlinear Analysis Real World Applications, 2015, 26: 191-198. [6] Liu Zhisu, Guo Shangjiang. On ground states for the Kirchhoff-type problem with a general critical nonlinearity[J]. J. Math. Annl. Appl, 2015, 426: 267-287. [7] Liu Jiu, Liao Jiafeng, Tang Chunlei. Positive solutions for Kirchhoff-type equations with critical exponent inRN[J]. J. Math. Annl. Appl, 2015, 429: 1153-1172. [8] Yang Yang, Zhang Jihui. Existence results for a class of nonlocal problems involving p-Laplacian[J]. Boundary Value Problems, 2011, 2011(1): 1-8. [9] Afrouzi G A, Chung N T, Shakeri S. Existence of positive solutions for Kirchhoff type equations[J]. Electronic Journal of Differential Equations, 2013(180): 118-130. [10] Liu Chunhan, Wang Jianguo, Gao Qingling. Existence of nontrivial solutions for p-Kirchhoff type equations[J]. Boundary Value Problems, 2013(1): 1-9. [11] Xiu Zonghu. The Existence of a Nontrivial Solution for a p-Kirchhoff Type Elliptic Equation inRN[J]. Abstract and Applied Analysis, 2013: 1056-1083. [12] Ourraoui A. On ap-Kirchhoff problem involving a critical nonlinearity[J]. Comptes Rendus Mathematique, 2014, 352(4): 295-298. [13] Guo Yuxia, Nie Jianjun. Existence and multiplicity of nontrivial solutions forp-Laplacian Schrödinger-Kirchhoff-type equations[J]. J. Math. Anal. Appl, 2015, 428: 1054-1069. [14] Rabinowitz P H. Minimax methods in critical point theory with applications to differential equations[M]. American Mathematical Soc, 1986. [15] Xuan Benjin. Variational methods-theory and applications[M]. He Fei: University of Science and Technology of China Perss, 2006. [16] Smets D. A concentration-compactness lemma with applications to singular eigenvalue problems[J]. Journal of Functional Analysis, 1999, 167: 463-480. [17] Júlio F, Corrêa S A, Figueiredo G M. On an elliptic equation ofp-Kirchhoff type via variational methods[J]. Bulletin of the Australian Mathematical Society, 2006, 74(2): 263-277.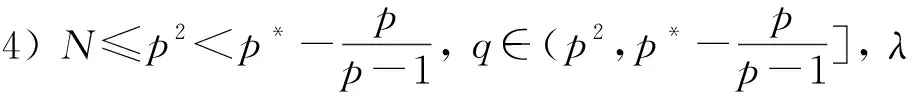
1 基本引理


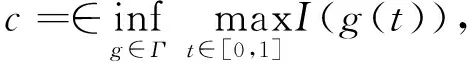



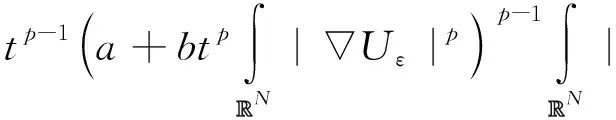

2 主要结论的证明












