概率有限状态机在动态效能评估中的应用

南 熠，伊国兴，王常虹，胡 磊，涂震飚

(1. 哈尔滨工业大学控制科学与工程系，哈尔滨 150080；2. 北京机电工程研究所，北京 100074)

0 引 言

武器作战效能是评价武器性能的重要指标[1-2]，效能评估在武器设计、制造及研发过程中起着重要作用[3-4]，并对武器的采购及作战方案的选择有着重要的参考意义[5-8]。随着武器技术的提升，武器系统的复杂化，各国军队需要采用更加客观、科学的武器性能测试及评价方法，武器作战效能评估得到了越来越多的重视[9]。

随着武器军事信息化技术的发展，武器系统间的相互影响、控制与决策系统的复杂化使得武器作战效能评估越来越困难。武器的作战效能不仅由武器自身性能决定，同时受到战场环境、敌方装备性能以及作战方案的影响[10]。反过来，作战效能评估的准确性影响着武器的制造、研发，以及作战方案的选择。传统的效能评估方法，如ADC法、多属性分析法、层次分析法等[11-12]，从武器自身特性出发，通过分析作战过程中武器自身表现出的可靠性、可用性、作战能力等特性，或对这些特性进行不同的加权来评估其作战效能。这些方法无法处理作战过程中出现的不确定性及模糊因素，所以许多学者提出了模糊评估方法，并将模糊理论与传统效能评估方法结合，提出了模糊层次分析法等[13-15]。同时，为了克服单一评估方法的缺点，将多种理论融合，得到的改进方法更具有针对性[8,16]。

然而，现有的效能评估方法多针对最终完成给定任务的可能性进行静态效能评估，而未对作战过程中实时变化的动态效能进行评估。考虑到作战全过程中，武器在不同阶段体现出的特性会因作战环境因素的变化而变化，文献[14]提出了效能的动态评估。与本文提出的动态效能评估不同，文献[14]分段分析武器的有效性、可靠性等性能，但评估结果也只是最终完成任务可能性的静态效能值，无法看到作战过程中环境变化及对抗因素的改变对武器作战能力的实时影响。

针对现有静态效能评估方法存在的缺点，本文将研究动态效能评估方法，从而帮助实现以下功能需求：

1)直观显示武器作战全过程中外部环境、对抗条件的变化对作战效能的影响程度，从而找到影响武器作战能力的关键因素，为武器的设计研发及采购提供参考；

2)直观显示作战过程中作战方案对作战效能的影响曲线，分析影响武器作战能力的关键作战阶段，从而在实际作战前辅助优化作战方案；

3)在实际作战过程中，实时评估战场信息空间对武器效能的影响，从而帮助进行实时作战方案调整。

为了满足实时战场需求，需要研究快速、准确的动态效能评估方法。基于仿真的方法已被许多先进国家采用[9,17]，该方法的评估准确性高，并能分析所有因素对效能的影响，可以用于动态效能评估。然后对于复杂、庞大的系统，难以建立精确模型，而模型的精确度对仿真结果的可信性影响较大[18]，并且运行一次仿真将耗费大量时间，无法满足实时性要求。另外，仿真方法以定量信息的表达方式为主，系统中重要的定性信息很难表达和获取[6]。

考虑到武器装备、战场环境、作战方案及作战目标这四个战场信息空间存在的不确定性及模糊性，以及对多元信息的处理需求。本文将采用概率有限状态机作为动态效能评估的基本方法，该方法的主要优点为：

1)有限状态机(Finite state machine, FSM)是对基于事件的控制逻辑建模的标准工具[19]，能够直观表示作战过程中，战场信息变化触发引起的武器系统状态改变，从而评估不同状态下的武器作战效能。

2)概率有限状态机(Probabilistic finite state machine, PFSM)可利用经验和直觉处理概率模型[20]，能够以概率的形式量化反映作战过程中，战场信息的不确定性等定性信息对武器作战效能的影响。

3)FSM根据系统工作模式建模，而非针对单次系统运行过程建模，即能够对同一类作战过程建模，满足系统模型包含不同战场信息空间对效能影响的需求。

利用FSM对武器对抗作战进行建模已有一定的应用。文献[19]利用FSM对雷达-导弹对抗体系进行了建模。虽然该文献主要利用该模型对雷达资源进行动态分配，而非动态效能评估，但可以看出该模型能够很好地描述对抗过程中各武器装备状态的动态变化。文献[21]利用PFSM来描述海军航空兵作战过程，并进行了作战效能评估。然而文中模型较为简单，不能很好地反映不同作战任务及作战方案对效能的影响，并未对作战全过程进行动态效能评估，无法分析影响效能的关键因素。

文章将分为以下几个部分对所提出的动态效能评估方法进行介绍。第1节将介绍本文所涉及到的主要概念及定义，包括动态效能评估的概念及λ-动态概率有限状态机(λ-Dynamic probabilistic finite state machine，λ-DPFSM)的定义。第2节将介绍利用λ-DPFSM建立武器对抗作战模型的方法及步骤，并给出动态效能评估的计算方法。第3节将以反舰导弹打击作战为例，动态评估其在不同战场信息下的作战效能，并分析影响其效能的主要因素。最后，第4节将对本文提出的方法进行总结分析。

1 概念及定义

效能评估可定义为对给定系统在一定条件下完成指定任务的能力[16,22-23]，用于描述效能信息的数据形式有许多种，如定量数字信息、区间、概率分布、定性判断信息以及语言变量等形式[1]，本文采用武器系统完成给定任务的可能性概率来描述武器作战效能。

相对于现有效能评估的定义，本文定义动态效能评估为，在给定系统执行指定任务的过程中，从任务开始到任务结束的每一时刻t(t≥t0，t0为任务开始时刻)，对系统完成任务可能性概率随时间变化而变化的函数值E(t)的估计。

对武器作战过程进行动态效能评估，则需对该过程进行建模。本文采用的建模方法是基于PFSM的改进方法，使其能够更好地满足实际需求。对于PFSM不同的学者和机构会根据自己的实际需求对其进行定义[20]。本文将在已有PFSM定义[24-26]的基础上，结合本文需求给出相应定义。而PFSM的基础结构是FSM，本文的建模方法也是从系统的FSM模型建立开始，所以首先将给出FSM的定义。

定义1. 有限状态机为一个四元组G:

G=S,X,Y,f

(1)

式中：

1)S为状态空间的非空有限集；

2)X为输入空间的非空有限集；

3)Y为输出空间的有限集；

4)f:S×X→S×Y为状态转移函数。

从时序角度理解转移函数f为：在第k次状态转移阶段(k∈N)，如果有转移前状态s(k-1)∈S，并有当前输入x(k)∈X，则系统转移为下一个状态s(k)并产生输出y(k)，即：

(s(k),y(k))=f(s(k-1),x(k))

(2)

并有s(0)为系统初始状态。

在FSM中，考虑当前状态及当前输入下，系统按照一定的概率分布转换为不同的下一状态或产生不同的输出时，就出现了PFSM。

定义2. 概率有限状态机为三元组K

K=G,π,I

(3)

式中：

1)G=S,X,Y,f为一个有限状态机;

2)I:S→[0,1]为初始状态概率，表示状态s∈S为初始状态的概率分布，并满足

(4)

3)π:S×X×S×Y→[0,1]为状态转移概率，其中对任意的s∈S，x∈X，s′∈S，y∈Y当π(s,x,s′,y)∈(0,1]时，有(s′,y)∈f(s,x)并满足：

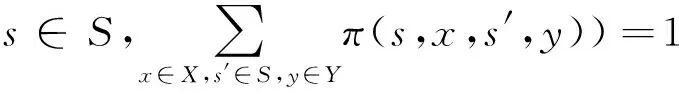
(5)

在PFSM中，考虑输入存在空(用λ表示)时，则会出现λ-PFSM[20]。λ-PFSM的定义与PFSM的定义基本相同，只需在状态机G=S,X,Y,f中的输入空间的非空有限集合X中加入空输入λ即可。

在实际作战过程中，不但需要考虑系统在相同输入下转换为不同后续状态的状态转移概率，如拦截导弹有一定的拦截成功概率；同时需要考虑输入的概率分布情况，如敌方发射拦截导弹的可能性。为了更加贴近实际需求，将定义λ-DPFSM，以满足如下几点：

1) 系统初始状态为我方武器系统准备状态，所以初始状态确定且唯一；

2)系统状态转换中不需要考虑系统输出；

3)系统输入存在一定的概率分布，并用λ表示概率上无输入的情况；

4)实际应用中，在系统当前输入无法匹配某一当前状态的有效输入时，该系统状态保持不变，并称该状态的当前输入为λ；

5)系统的状态转移概率及输入概率分布是动态的，由状态转移时刻的系统环境及参数决定。

定义3. λ-DPFSM是一个五元组D

D=S,X,f,u,π

(6)

式中：

1)S为非空状态空间的有限集；

2)X为包含λ的非空输入空间集合；

3)f:S×X→S为状态转移函数，并对∀s∈S满足：f(s,λ)=s;

4)π:S×X×S×k→[0,1]为第k次状态转移概率，其中k∈N表示当前状态转移的步数，其中对任意的s∈S，x∈X，s′∈S，k∈N当π(s,x,s′,k)∈(0,1]时，有s′∈f(s,x)，并对任意给定s∈S,x∈X,k∈N满足：

(7)

6)u:S×X×k→[0,1]为第k次状态转移时，对应的输入概率，并对任意给定s∈S,k∈N满足：

(8)

可以看出，在λ-DPFSM中，在第k∈N步状态转换时，当前状态s∈S在输入x∈X的作用下转换为下一状态s′∈S的概率Pk(s→s′)为:

Pk(s→s′)=π(s,x,s′,k)×u(s,x,k)

(9)

2 动态效能评估步骤

对武器作战过程进行动态效能评估 (Dynamic efficiency evaluation, DEE)，需要对其进行建模分析，建模过程需要考虑武器性能、战场环境等对作战过程的影响。本文在系统建模时考虑的主要影响因素包括四方面：

1)武器装备信息空间，即武器装备的自身性能，其会影响作战过程中的系统状态、能够对系统状态产生影响的输入，以及状态转移概率；

2)战场环境信息空间，即作战过程中的外部环境条件，其会影响系统输入，从而影响系统状态的转移及转移概率；

3)作战方案信息空间，其会影响单次作战的具体步骤，从而影响系统状态转换过程及转移概率；

4)作战目标信息空间，即打击目标的特性空间，其会影响敌方能够采取的对抗方案，以及对抗能力效果，从而影响系统输入概率及系统状态转移概率。

利用λ-DPFSM方法进行武器作战动态效能评估的主要步骤如图1所示。

1)系统状态及输入提取

根据武器装备信息及战场环境，分析提取系统状态S以及系统输入X。系统状态S描述了武器装备在作战过程中的行为或表现出的特点，如武器是否受到拦截、干扰等。系统输入X代表着武器作战过程中可能遇到的各种地形、天气等环境因素，以及敌方单位可能做出的各种拦截、干扰等对抗措施。

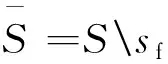
2)建立FSM模型

根据系统输入与系统状态之间的相互影响，确定系统的状态转移函数f:S×X→S，建立武器作战过程的FSM结构模型：

G=S,X,f

描述对抗过程中武器系统状态可能发生的转换。

这里建立的FSM结构模型并不是针对某次作战过程，而是对相同作战模式下同类型武器作战过程的概括。如对于导弹打击目标的过程，都会经历巡航、拦截、干扰、打击目标等一个或多个阶段，对这些阶段进行分析建模，其状态转换结构模型相同，仅经历各阶段的时间顺序或次数由具体作战过程决定。

建立FSM模型过程中，可能需要对系统状态的选取进行调整，以使模型能够体现所有可能对武器作战效能产生影响的事件。所以步骤1与步骤2相互影响，需要进行反复调整，以满足效能评估对模型准确度的需求。

3)将单次作战时序命令输入FSM模型，得到该次作战状态转移时序。

根据某次具体作战中作战目标的特性，设计具体的作战方案，得到该次作战过程的系统输入指令x(k)(k∈N，表示第k次状态转移)，将x(k)代入建立的FSM结构模型中，根据状态转移函数f，可以得到此次作战过程的状态转移时序s(k)(k∈N)，并有：

(10)

式中：s0为系统的初始状态，由武器装备自身特性决定。

同时作战环境、武器属性及目标属性的不同，决定着实际系统输入概率u(s(k-1),x(k),k)→[0,1](k∈N)，及状态转移概率π(s(k-1),x(k),s(k),k)→[0,1](k∈N)。如作战环境及敌方装备的不同决定着敌方是否对友方导弹进行拦截，友方导弹的型号及拦截导弹的型号决定着单次拦截的成功概率，这两个概率共同决定着友方导弹能够突防的可能性。

状态转移概率的准确性影响着效能评估结果的准确性，状态转移概率的获取方法可分为三种：1)理论分析法，2)仿真模拟法，3)专家经验法。搭建系统的数学、物理模型，利用理论分析法获得的状态转移概率值最为精确，然而对于复杂、庞大的系统，建立其精确的数学模型是不实际的。所以，本文利用专家经验及仿真模拟相结合的方法来获得状态转移概率，并根据系统复杂度及专家经验知识分为两种方法：1)对于简单系统，由专家经验给出概率值，并利用蒙特卡洛法[27]，进行少量仿真校验；2)对于专家经验无法给出的概率值，进行大量仿真，利用蒙特卡洛法统计得出。

FSM结构模型能够反映一系列武器作战过程，而状态转移时序则反映单次作战的具体过程，是战场信息对系统状态影响的具体表现。根据状态转移时序则可以对该次作战进行动态效能评估。

4)动态效能评估

在得到状态转移时序的同时，根据实际状态转移概率，可以计算某一事件触发下系统处于不同状态的概率，从而进行动态效能评估。根据系统状态sf的定义，计算某一t时刻(t≥t0，t0为作战过程初始时刻)系统的动态效能评估值E(t)为：

(11)

(12)

式中：k∈N+；P(s0)表示系统处于初始状态s0的概率，并有P(s0)=1；tk表示第k次状态转换的发生时间；Pk(s)表示第k次状态转换后系统状态为s∈S的概率，其计算式为：

(13)

Pk(s′→s)为第k次状态转换中，系统状态从s′转换为s的概率，根据式(9)，对给定s′=s(k-1)，s=s(k)有：

Pk(s′→s)=π(s(k-1),x(k),s(k),k)×

u(s(k-1),x(k),k)

(14)

5)效能影响因素分析

根据动态效能评估的结果，分析影响该次作战效能的主要因素。在实际作战过程中，由于系统无法从状态sf转换为其它系统状态，又Pk(s→sf)≥0，可以看出：

是时间的减函数。另外由于E(tk)∈[0,1]，在作战末期，系统输入对作战效能影响的程度将很难从效能值变化的大小上分析。为了更清楚地分析不同时期系统输入对作战效能的影响程度，本文提出了相对效能值ER(t)，以表征单次状态转换对效能的影响。其计算式为：

(15)

ER(t)可以理解为只考虑当前时段内系统输入对效能的影响而不考虑之前输入的累积作用。所以一般认为,ER(t)的值越小，该时段内系统输入对效能的影响越大。获知影响武器作战效能的关键影响因素后，可以在武器设计阶段提供重要参考，并在作战前辅助优化作战方案。而效能评估结果的准确性及改进作战方案的有效性将利用仿真试验或半实物仿真试验进行校验。

3 反舰导弹作战动态效能评估

本文以反舰导弹为例，给出利用λ-DPFSM方法进行动态作战效能评估的具体步骤，并以某型号导弹打击某型号舰船为例，分析影响其作战效能的主要因素。

1)系统状态及输入提取

导弹打击过程一般包括巡航段和打击段，巡航段又包括高飞定位和低飞巡航；各飞行段都可能遇到敌方拦截及干扰，而高飞定位可能被敌方探测发现，低飞巡航可能会因地势变化而撞击地面；导弹进入打击段后由于已十分接近目标，所以不存在未被敌方探测到的状态。由此，提取系统状态si以及系统输入xi如表1所示。

需要说明的是，在系统的λ-DPFSM模型中，系统的可靠性通过可靠性损失概率体现。在本例中，导弹的可靠性计算于发射阶段，即：P1(s0→sf)=π(s0,x1,sf,1)中包括导弹发射失败概率及导弹的可靠性损失概率。

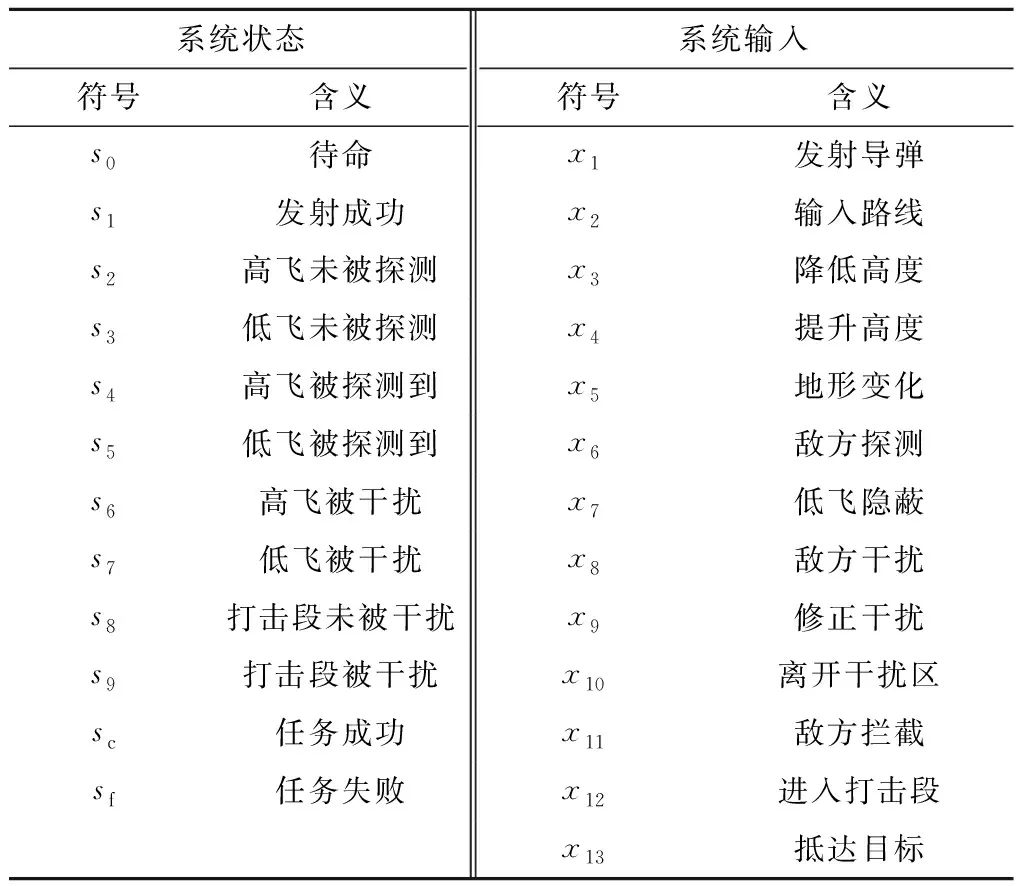
表1 系统符号及含义Table 1 Corresponding meanings of system symbols

2)根据导弹打击目标作战过程中系统输入对系统状态的影响关系，建立FSM结构模型如图2所示，其中,xi=x8,x11;xj=x5,x7,x8,x11。

将状态sf删除以对该模型进行简化，得到的新模型如图3所示。而对模型进行简化则至少需要满足以下两个条件之一：

(1)简化过程中删除的系统状态应为评估需求不关注，且不会影响后续状态转换的状态节点。

(2)若所有节点均为关注节点，则最多可删除一个无后续状态的状态节点，同时可利用下式：

(16)

计算由状态s转换为被删除状态s″的概率，从而减小模型的存储空间。简化后的系统模型不再完全满足式(5)，而是满足:

(17)

3)单次作战状态转移时序

根据实际作战方案，敌友双方武器装备性能，以及对作战环境的分析，可以得到系统的输入时序、输入概率分布，及状态转移概率。将输入时序代入到武器作战FSM结构模型中，可得到单次作战效能转换时序图。导弹打击某型号舰船A的具体作战飞行轨迹如图4所示，相应的状态转移时序如图5所示。

4)动态效能评估

根据动态效能的计算式(11)，在得到状态转移时序图的同时，可以得到该次作战过程中武器作战动态效能评估曲线如图6所示。通过动态效能评估，能够清楚地看到作战过程中系统输入对效能产生的影响，如外部环境变化、敌方对抗措施对友方武器作战效能的影响。

由于FSM结构模型反映一系列武器作战过程，所以评估不同战场信息对武器效能的影响，只需将具体作战过程的输入时序带入同一FSM结构模型中。如利用相同的导弹以相同的飞行轨迹打击无拦截防御系统的舰船B，其状态转移时序及动态效能评估结果分别如图7和图8所示。

从图7～8可以看出，利用武器作战FSM结构模型，评估不同战场信息空间对武器效能的影响，分析影响武器作战效能的关键因素，则需要不断调整战场信息并重新将系统输入带入同一FSM模型进行效能评估。

5)效能影响因素分析

为了快速分析作战过程中影响武器作战效能的关键因素，在进行动态效能评估的同时，计算其相对效能值ER(t)，ER(t)值越小则表示该时段内系统输入对效能的影响越大。以导弹打击A舰船为例，计算其相对效能值ER(t)，与E(t)对比结果如图9所示。从图9可以看出，远程拦截对E(t)值变化的影响最大，但中程拦截处的ER(t)值最小。而实际情况是，在受到干扰时中程拦截的拦截概率略高于远程拦截。可以看到ER(t)值能更准确地反映出影响效能的关键因素。

根据效能影响因素分析结果，在该次作战过程中为了提高导弹的作战效能，则需要重点提高其反拦截能力。为了达到该目标，在武器设计阶段加入了诱饵弹，以干扰敌方拦截弹；并在作战方案设计时尽可能减少巡航段的高飞时间，以降低我方导弹的被探测概率从而减小远程拦截概率。修改作战方案及武器性能后，在同一对抗作战环境下进行动态效能评估结果如图10所示。

从图10可以看出，修改后我方导弹的反拦截能力有较大提升，但由于高飞定位段时间减少，导致导航准确度有所下降，但武器总体作战能力有所提升。

4 结束语

本文提出了动态效能评估的概念，给出了利用λ-DPFSM进行动态效能评估的方法步骤，并以某反舰导弹打击目标为例进行了建模仿真。该评估方法的优点在于：1)以输出效能时间曲线的形式直观反映了武器作战过程中效能的变化程度；2)考虑了四个战场信息空间对效能的影响，并以概率的形式反映了系统中存在的不确定性；3)建立的FSM模型能够反映同一系列武器的作战过程，而不需要针对单次作战进行建模。从仿真结果可以看出，该方法能够实现对武器作战过程进行动态效能评估，并分析影响效能值的关键因素。利用分析结果提出的武器性能改进方案及优化的作战方案，能够有效提高武器作战能力。

参 考 文 献

[1] Yin D, Wang H. An evidential reason approach for operational effectiveness evaluation of weapon system under uncertain[C]. 2010 International Conference on Computer Application and System Modeling, Taiyuan, China, October 22-24, 2010.

[2] 张克, 刘永才, 关世义. 关于导弹武器系统作战效能评估问题的探讨[J]. 宇航学报, 2002, 23(2): 58-66.[Zhang Ke, Liu Yong-cai, Guan Shi-yi. An investigation into the problem of evaluating combat effectiveness for missile weapon systems[J]. Journal of Astronautics, 2002, 23(2): 58-66.]

[3] Li Z, Zhang S, Wang J, et al. Research on description method of operational task oriented to operational effectiveness evaluation[J]. AsiaSim 2012, 2012: 313-321.

[4] Ning X, Yuan J, Yue X, et al. Evaluating of operational effectiveness of electro-optical imaging reconnaissance satellite[C]. The 2nd International Conference on Space Information Technology, Wuhan, China, November 10-11, 2007.

[5] Li Z, Li J, Liu S, et al. Design and implementation of operational effectiveness evaluation simulation system for ECM[C]. The 1st International Conference on Innovative Computing, Information and Control, Beijing, China, August 30-September 1, 2006.

[6] Huang Y, Jiang R, Chi S, et al. Evaluation method of weapon equipment operational effectiveness based on Belief Map[C]. 2011 International Conference on Information Science and Technology, Nanjing, China, March 26-28, 2011.

[7] Li J, Nie C, Wang L. Overview of weapon operational suitability test[C]. 2016 International Conference on Artificial Intelligence and Engineering Applications, Hong Kong, China, November 12-13, 2016.

[8] Xia W, Liu X,Meng S, et al. Efficiency evaluation research of missile weapon system based on the ADC-II model[C]. The 6th International Conference on Machinery, Materials, Environment, Biotechnology and Computer, Tianjin, China, June 11-12, 2016.

[9] Gim Y K, Kang J H. A study on the operational test and evaluation in applying modeling and simulation to guided weapon systems-Focus on Hyun-Gung project[J]. Journal of the Korea Association of Defense Industry Studies, 2013, 20(1): 20-44.

[10] Li Z F, Yuan H, Yang F. SCA based exploratory evaluation of weapon equipment operational effectiveness[C]. The 4th International Conference on Manufacturing Science and Engineering, Dalian, China, March 30-31, 2013.

[11] Shao X F, Chen Q. Complication evaluation of methods of naval battlefield electromagnetic environment based on combat effectiveness[J]. Applied Mechanics and Materials, 2014, 565:233-237.

[12] 杨卓鹏, 郑恒, 角淑媛, 等. 一种导航卫星的系统效能建模与分析方法[J]. 宇航学报, 2017, 38(6): 647-654.[Yang Zhuo-peng，Zheng Heng，Jiao Shu-yuan，et al. A system effectiveness modeling and analysis method of single navigation satellite[J]. Journal of Astronautics, 2017, 38(6): 647-654.]

[13] Xia Z, Xu L, Fan W. Evaluation of operational effectiveness for TWS based on fuzzy probability[C]. The 6th International Symposium on Computational Intelligence and Design, Hangzhou, China, October 28-29, 2013.

[14] Dou J. Ship-to-air missile system operational effectiveness evaluation credibility analysis[C]. 2016 International Forum on Energy, Environment and Sustainable Development, Shenzhen, China, April 16-17, 2016.

[15] Zhao Y P, Li N. The evaluation in weapon operational effectiveness base on fuzzy analytic hierarchy process[C]. The 2nd International Conference on Manufacturing Science and Engineering, Guilin, China, April 9-11, 2011.

[16] 梁金登, 李东旭. 空间武器系统效能评估模型研究[J]. 宇航学报, 2007, 28(5): 1422-1428.[Liang Jin-deng, Li Dong-xu. Research on effectiveness evaluation model of space weapon system[J]. Journal of Astronautics, 2007, 28(5): 1422-1428.]

[17] Huang Y Y. A methodology of simulation and evaluation on the operational effectiveness of weapon equipment[C]. The 21st Chinese Control and Decision Conference, Guilin, China, June 17-19, 2009.

[18] Brennan J F M, DentonA L. COMPASS—the verification and validation of an operational analysis model for use in the prediction of Nimrod MRA4 operational effectiveness[J]. Journal of the Operational Research Society, 2004, 55(4): 413-421.

[19] Seok J, Zhao J, Selvakumar J, et al. Radar resource management: dynamic programming and dynamic finite state machines[C]. The 12th European Control Conference, Zurich, Switzerland, July 17-19, 2013.

[20] Vidal E,Thollard F, De La Higuera C, et al. Probabilistic finite-state machines-part I[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(7): 1013-1025.

[21] 刘小玲, 潘巨辉, 金雷, 等. PFSM 在海军航空兵作战仿真中的应用研究[J]. 系统仿真学报, 2011, 23(5): 853-856.[Liu Xiao-ling, Pan Ju-hui, Jin Lei, et al. Research on application of probabilistic finite-state automata to battle simulation of naval air force[J]. Journal of System Simulation, 2011, 23(5): 853-856.]

[22] Zhou D, Zhang A, Chang H, et al. Research on operational effectiveness of space-based weapon and sensitivity analysis[C]. The 8th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, December 13, 2016.

[23] 周伟, 罗建军, 郝辉. 固体运载火箭多级组合优选多属性评价方法[J]. 宇航学报, 2017, 38(2): 115-122.[Zhou Wei, Luo Jian-jun, Hao Hui. Multi-attribute evaluation method for multi-stage combined optimization of solid rocket[J]. Journal of Astronautics, 2017, 38(2): 115-122.]

[24] Mukherjee K, Ray A. State splitting and merging in probabilistic finite state automata for signal representation and analysis[J]. Signal Processing, 2014, 104: 105-119.

[25] 曹源, 梁华国, 黄正峰, 等. 基于 Markov 链的 FSM 容软错误设计[J]. 宇航学报, 2011, 32(3): 665-670.[Cao Yuan, Liang Hua-guo, Huang Zheng-feng, et al. FSM soft fault-tolerant design based on Markov chain model[J]. Journal of Astronautics, 2011, 32(3): 665-670.]

[26] Zhang F, Cheung T. Optimal transfer trees and distinguishing trees for testing observable nondeterministic finite-state machines[J]. IEEE Transactions on Software Engineering, 2003, 29(1): 1-14.

[27] 金振中, 袁刚, 贾旭山. 防空导弹对机动目标杀伤效果分析[J]. 宇航学报, 2007, 28(5): 1419-1421.[Jin Zhen-zhong, Yuan Gang, Jia Xu-shan. Interception efficiency analysis of antiaircraft missile intercepting a maneuver target[J]. Journal of Astronautics, 2007, 28(5): 1419-1421.]