带有入轨姿态约束的迭代制导算法及应用研究

韩雪颖，马 英，张志国，余梦伦

(北京宇航系统工程研究所，北京 100076)

0 引 言

对我国现役运载火箭来说，在大气层内采用固定程序角飞行，在大气层外飞行段采用摄动制导方法，基本能够满足准确入轨的要求[1]。随着航天领域及相关技术的发展[2]，运载火箭发射任务呈现多样性，对制导精度也提出了更高的要求，摄动制导已经无法满足，需要研究适应能力更强、制导精度更高的自适应制导算法。迭代制导方法是自适应制导诸算法中应用最多的一种[3]。该方法以最优控制理论为基础，根据火箭飞行瞬时状态和终端目标，实时确定出一组最优控制姿态角[4]，具有制导精度高、任务适应性强、箭上飞行软件简单、诸元装订少等优点[5]。1967年，Doris C.Chandler和Isaac E.Smith首先给出了迭代制导方法[6]，该方法在国外得到广泛应用，美国的“土星五号”运载器[7]，欧空局的阿里安火箭、俄罗斯的“能源号”重型运载火箭等都采用了迭代制导技术[8]。国内学者韩祝斋[4]、陈新民、余梦伦[3]、茹家欣[9]等也先后进行了相关研究，并通过仿真证明了迭代制导方法的有效性。目前迭代制导已在我国载人运载火箭及新一代运载火箭上得到成功应用。

传统的迭代制导方法，在发动机推力不可调节的情况下，以终端点的三个速度分量和两个位置分量为约束条件，得到近似处理后的控制角表达式由常值部分和与时间一次项相关的部分相加而成，其中前者为使火箭满足入轨点速度约束所需的部分，后者为在速度约束基础上再使火箭满足入轨点位置约束所需的小量部分。实际上，在运载火箭承担的发射任务中，某些有效载荷对入轨姿态有着较为严格的要求(如对地定向、测控等)，使得运载火箭需要满足一定的入轨姿态约束[10]。在这种约束条件下，传统的迭代制导方法已无法适用。

针对带有入轨姿态约束的运载火箭制导问题，吕新广等[10]提出了一种将传统迭代制导与数值积分相结合的轨迹预测制导方法，能够同时满足入轨姿态约束和轨道参数约束要求，由于多次数值积分计算带来大计算量，需要采取多处理器并行等措施缩短运算时间。张志国等[11]基于轨迹优化理论，研究了应用伪谱法的运载火箭在线制导方法，仿真结果表明该方法在保证入轨精度的同时，可有效处理带入轨姿态约束的火箭制导问题，但需要通过选择合适的基点数量和制导周期平衡制导效率和制导精度的关系。邱丰、宋征宇[12]结合直接配点法[13]和伪谱法[14]，提出了一种基于联立框架的直接法，入轨精度和入轨大姿态约束均能满足，与伪谱法相比，计算效率得到大幅提高。本文在传统迭代制导算法的基础上，针对只能控制发动机的推力方向，而不能改变发动机推力大小的运载火箭，通过在控制角表达式中增加与时间二次项相关的部分，在满足入轨点三个速度约束和两个位置约束的同时，也能实现对入轨俯仰、偏航姿态角的有效控制，且与传统迭代制导相比，计算量增加少，能够满足箭上实时计算需求，适合工程应用。

1 迭代制导问题描述

为简化制导控制方程形式，将运载火箭动力学方程建立在目标点轨道坐标系Os-εηζ，其中坐标系原点Os为地心，Osη轴由地心指向入轨点，Osε轴与Osη轴垂直，且与当地水平面平行，指向运载火箭运动方向，Osζ轴与Osε轴、Osη轴构成右手定则。在目标点轨道坐标系计算的控制角需要通过坐标变换转至发射惯性系中，转换关系参见文献[8]。不考虑大气影响，真空飞行段火箭的动力学方程为

(1)

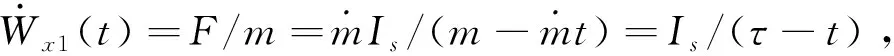
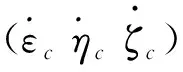
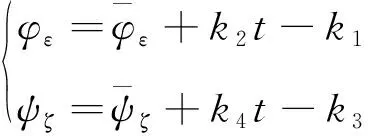
(2)

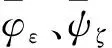
在传统迭代制导算法中，控制角φε、ψζ的表达式均是与时间相关的线性函数，通过控制剩余飞行时间和对k1、k2、k3、k4进行调节，可以实现对入轨点三个速度分量和两个位置分量的有效控制，但没有对入轨姿态进行控制，因此无法满足入轨姿态约束的要求，且在各项干扰作用下，入轨姿态散布较大[1]，这对某些有入轨姿态要求的有效载荷产生一定影响。为此需要研究能够同时满足运载火箭入轨速度、位置和姿态约束的制导算法。

2 有入轨姿态角约束的迭代制导算法

2.1 入轨点有姿态角约束时控制角的表达式

为了实现对入轨姿态角的控制，本文在传统迭代制导算法的基础上，将控制角的最优解经二阶近似展开，得到如下形式的控制角近似解表达式

(3)

式(3)是与时间相关的二次函数，与式(2)相比，增加了两个参数k5、k6，通过对六个参数k1、k2、k3、k4、k5、k6的调节，可以在满足速度与位置约束的同时，也能满足姿态约束。

假设有效载荷对入轨姿态的要求对应火箭在目标轨道坐标下的入轨姿态角为φεc、ψζc，由式(3)可知，其应满足

(4)

在入轨点只有速度约束的情况下，需增视速度为

(5)

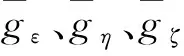
(6)

这是为简化计算所作的近似处理，随着火箭接近入轨点，平均引力所代表的真实性也随之增强，故这种近似处理不会影响入轨精度[3]。

根据欧拉角产生的关系：

(7)

式(7)表明，火箭飞行瞬时，为满足入轨点速度约束产生的控制角是一组瞬时常值。

2.2 有入轨姿态角约束时的迭代制导方程

假设k5t2+k2t-k1、k6t2+k4t-k3均为小量，对小量，有下式成立

(8)

(a)偏航姿态控制方程

将式(3)和式(6)代入式(1)中第三式，得到

(9)

式中：

(10)

将式(8)代入式(10)，得到

(-k3+k4t+k6t2)

(11)

将式(11)代入式(9)，并进行一次积分，得到

(12)

式中：

(13)

(14)

(15)

(16)

对式(12)两边再次积分，得到

(17)

式中：

(18)

(19)

(20)

(21)

联立姿态约束方程(4)中第二式以及式(16)、式(21)，得到

(22)

(b)俯仰姿态控制方程

同样地，将式(3)和式(6)代入式(1)中第二式，并进行两次积分，可得到

(23)

(24)

式中：

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

联立姿态约束方程(4)中第一式以及式(23)、式(24)，得到

(33)

求解式(22)和式(33)可以得到k1～k6，和式(7)一起代入式(3)，可以得到实时计算的控制角。

(c)火箭剩余飞行时间的确定

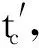
(34)

式中：

(35)

(36)

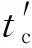
(37)

式(34)和式(37)经制导计算机迭代计算，可以求得满足一定精度要求的剩余飞行时间。

3 仿真校验

以某带助推两级运载火箭发射900 km太阳同步轨道任务为例对本文算法的应用进行仿真分析。根据推质比变化，火箭二级分为大推力工作段和小推力工作段。仿真时选择迭代制导在小推力工作段开始后10 s加入，至发动机关机前5s结束，此时间段内火箭推质比变化较小，发动机工作平稳。标准弹道入轨点程序角φc=-34.7°，ψc=-11.8°。

(1)与传统迭代制导对比

以标准弹道入轨点程序角作为入轨姿态角约束，分别采用传统迭代制导和带有入轨姿态约束的迭代制导进行零干扰弹道计算，得到控制姿态角与标准弹道程序角的对比曲线见图1、图2。考虑火箭各项方法误差，包括火箭质量、质心参数偏差、发动机性能参数偏差、大气参数偏差等，得到两种制导算法入轨点参数偏差的对比情况见表1。

从图1、图2曲线可以看出，与传统迭代制导相比，采用带有姿态约束的迭代制导算法生成的入轨点控制姿态角与入轨姿态约束值之间的偏差更小，同时由于在算法刚加入时刻对终端姿态角估计精度不高，与终端约束值差异较大，表现出的姿态角跳变比传统迭代制导仅由模型简化造成的初始姿态角跳变更大一些。通过姿态角速率限幅等措施，可以对跳变进行适当平缓，确保姿态控制效果。

表1数据表明，采用带有入轨姿态角约束的迭代制导和传统迭代制导算法的入轨点轨道根数偏差水平相当，且前者使入轨姿态角偏差显著减小。

表1 入轨点参数偏差对比Table 1 Comparison of the injection parameter deviation

为了评估采用本文算法对运载能力的影响情况，进行10 000次蒙特卡洛打靶仿真计算，并按照零干扰弹道剩余量进行无量纲化处理，得到末级推进剂剩余量散布对比情况见图3，其中1～10 000次是采用传统迭代制导的情况，10 001～20 000次是采用带有入轨姿态角约束的迭代制导的情况。

由图3可以看出，与传统迭代制导相比，采用本文算法会使火箭末级推进剂剩余量散布略大。数据统计结果表明，以标准弹道入轨点程序角为约束，在正常偏差情况下，采用本文算法，二级安全余量需求将增加5%，相应的运载能力仅损失1%。

(2)故障适应性

为验证本文迭代制导算法在故障工况下的适应性，针对以下典型故障工况进行仿真分析：某一时刻(420 s、520 s)发动机出现故障，推力下降25%。

不考虑入轨姿态约束，采用传统迭代制导得到的零干扰弹道俯仰、偏航程序角曲线见图4、图5。考虑以标准弹道入轨点程序角作为入轨姿态约束，采用带入轨姿态约束的迭代制导得到的零干扰弹道俯仰、偏航程序角曲线见图6、图7。两种算法在故障工况下入轨点轨道参数及姿态偏差的比对情况见表2。

从图4～图7可以看出，两种算法对故障均具有较强的自适应能力，只是在发动机出现推力下降瞬时，控制姿态角均会出现跳变，与标准弹道差异增大，可以通过程序角速率限幅等措施，避免出现瞬时大幅跳变，保证姿态控制平稳。与此同时，采用带有入轨姿态约束的迭代制导能够使零干扰故障弹道下的入轨姿态与理论弹道入轨程序角差异更小。

故障时刻制导方法|ΔT|/s|Δa|/km|Δi|/(°)|Δe||Δφc|/(°)|Δψc|/(°)420 s传统迭代制导124.930.4730.0240.000476.656.59姿态角约束迭代制导125.850.6780.0230.000453.961.49520 s传统迭代制导91.060.5730.0240.000457.436.17姿态角约束迭代制导92.860.6770.0230.000431.701.46

对比表1、表2，故障工况下，采用两种算法均会使火箭飞行时间显著延长。入轨姿态角偏差虽也均有增加，但由于带入轨姿态约束的迭代制导为满足故障工况下的入轨姿态约束，对剩余飞行过程中的姿态进行了一定范围的调整，使该方法下的入轨姿态偏差依然较小。除此之外，两种算法下的入轨参数偏差水平相当，火箭依然能够按预定目标飞行。

相比正常工况，故障工况下采用本文算法后的二级推进剂剩余量散布情况见图8(无量纲化结果)。

统计结果表明，在发动机推力下降25%的故障工况下，二级推进剂剩余量散布相比正常工况更小，且故障时间越早，散布越小。在420s故障工况、520s故障工况下，二级安全余量需求分别减小9%、5%，相应的运载能力分别提升2%、1%，这是由于在故障发生后，采用带有入轨姿态角约束的迭代制导，能够根据火箭当前状态重新进行弹道规划，充分利用了发射高轨任务末级小推力长时间推进的优势，使得二级安全余量需求降低，运载能力反而有所提高。但由于目前该型发动机尚不具备节流能力，故在正常工况下无法利用这个优势提升火箭运载能力。

(3)不同姿态角约束对比

分别设置不同的入轨姿态角约束进行仿真分析，其零干扰弹道下的俯仰、偏航程序角曲线见图9、图10。不同姿态角约束下的入轨点参数偏差见表3。

图9、图10及表3数据表明，对不同入轨点姿态约束，采用带有姿态角约束的迭代制导算法在保证较高精度入轨的同时，也能满足入轨点姿态约束的要求。结果也表明:随着入轨点姿态角约束与标准弹道入轨点程序角差异越来越大，入轨点姿态角偏差有所增大。为满足入轨点姿态约束，入轨位置精度会有所损失，因此，该算法能够适应一定范围内的入轨点姿态角约束，当入轨点姿态约束偏离理论弹道入轨点程序角太大时，会导致入轨精度变差，相应的运载能力损失增大，甚至会使姿态发散。在这种情况下，应该综合权衡有效载荷对入轨点位置约束及姿态约束的具体要求使用该算法，若无法同时满足，可以考虑在火箭末级增加调姿系统等方式，达到同时满足火箭入轨速度、位置及姿态角约束的要求。

入轨点姿态约束|ΔT|/s|Δa|/km|Δi|/(°)|Δe||Δφc|/(°)|Δψc|/(°)φc=-25°ψc=-11.8°9.311.4930.0310.000602.570.92φc=-45°ψc=-11.8°9.481.2170.0310.000632.651.10φc=-50°ψc=-11.8°9.221.5460.0320.000643.801.17φc=-34.7°ψc=-8°8.890.6910.0320.000640.961.33φc=-34.7°ψc=-13°8.970.5620.0320.000621.111.23φc=-40°ψc=-13°9.400.9480.0320.000621.611.28

4 结束语

针对有入轨姿态要求的运载火箭发射任务，本文在传统迭代制导算法的基础上，通过将控制角的表达式近似展开为与时间相关的二次函数，推导出能够满足入轨姿态角约束的迭代制导算法。对某运载火箭发射任务的仿真结果表明，与传统迭代制导算法相比，采用本文推导的迭代制导算法在运载能力损失不多的情况下，可以实现同等水平的入轨精度，同时又能很好地满足入轨姿态约束，对故障的自适应能力较强，且计算量增加少，易于工程实现。

参 考 文 献

[1] 宋征宇. 从准确、精确到精益求精——载人航天推动运载火箭制导方法的发展[J]. 航天控制, 2013, 31(1):4-10. [Song Zheng-yu. From accurate, precise to perfect-manned space promotes the development of guidance method on launch vehicle [J]. Aerospace Control, 2013, 31(1): 4-10.]

[2] 鲁宇. 中国运载火箭技术发展[J]. 宇航总体技术, 2017, 1(3):1-8. [Lu Yu. Space launch vehicle′s development in china [J]. Astronautical Systems Engineering Technology, 2017, 1(3):1-8.]

[3] 陈新民, 余梦伦. 迭代制导在运载火箭上的应用研究[J]. 宇航学报, 2003, 24(5):484-489. [Chen Xin-min, Yu Meng-lun. Study of iterative guidance application to launch vehicles [J]. Journal of Astronautics, 2003, 24(5): 484-489.]

[4] 韩祝斋. 用于大型运载火箭的迭代制导方法[J]. 宇航学报, 1983, 1(1):11-20. [Han Zhu-zhai. An iterative guidance method for the large launch vehicle [J]. Journal of Astronautics, 1983, 1(1): 11-20.]

[5] 李超兵, 吕新广, 王志刚, 等. 一种适用于目标圆轨道的空间变轨迭代制导算法研究[J]. 航天控制, 2015, 33(3):34-37. [Li Chao-bing, Lv Xin-guang. Wang Zhi-gang, et al. Research on Iterative Guidance Algorithm for Spacecraft Orbit Transfer [J]. Aerospace Control, 2015, 33(3):34-37.]

[6] Chandler D C, Smith I E. Development of the iterative guidance mode with its application to various vehicles and missions [J]. Journal of Spacecraft and Rockets, 1967, 4(7):898-903.

[7] Haeussermann W. Saturn launch vehicle′s navigation, guidance and control system [J]. Automatica , 1971, 7(5): 537-556.

[8] 李伟. 基于精确控制解的运载火箭迭代制导自适应性分析研究 [D]. 哈尔滨: 哈尔滨工业大学, 2012. [Li Wei. Research and analysis on iterative guidance self-adaptability of vehicle base on precise control of solution [D]. Harbin: Harbin Institute of Technology, 2012.]

[9] 茹家欣. 液体运载火箭的一种迭代制导方法[J]. 中国科学, 2009, 39(4):696-706. [Ru Jia-xin. An iterative guidance method of liquid rocket [J]. Science in China, 2009, 39(4): 696-706.]

[10] 吕新广, 宋征宇, 巩庆海. 运载火箭轨迹预测制导方法研究[J]. 载人航天, 2013, 19(6):20-24. [Lv Xin-guang, Song Zheng-yu, Gong Qing-hai. Research on trajectory prediction guidance for launch vehicle [J]. Manned Spaceflight, 2013, 19(6):20-24.]

[11] 张志国, 余梦伦, 耿光有, 等. 应用伪谱法的运载火箭在线制导方法研究[J]. 宇航学报, 2017, 38(3):262-269. [Zhang Zhi-guo, Yu Meng-lun, Geng Guang-you, et al. Research on application of pseudo-spectral method in online guidance method for a launch vehicle [J]. Journal of Astronautics, 2017, 38(3): 262-269.]

[12] 邱丰, 宋征宇. 采用联立法求解大姿态终端约束的上升段轨迹优化[J]. 宇航学报, 2017, 38(1):18-25. [Qiu Feng, Song Zheng-yu. Large terminal attitude constrained trajectory optimization of ascent stage via simultaneous method [J]. Journal of Astronautics, 2017, 38(1): 18-25.]

[13] 邱丰, 宋征宇. 基于联立框架的轨迹优化算法[J]. 航天控制, 2015, 33(2):9-15. [Qiu Feng, Song Zheng-yu. A trajectory optimization algorithm based on simultaneous strategies[J]. Aerospace Control, 2015, 33(2): 9-15.]

[14] 杨希祥, 张为华. 基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究[J]. 宇航学报, 2011, 32(1):15-21. [Yang Xi-xiang, Zhang Wei-hua. Rapid optimization of ascent trajectory for solid launch vehicles based on gauss pseudo-spectral method[J]. Journal of Astronautics, 2011, 32(1): 15-21.]

[15] 吴楠, 程文科, 王华. 运载火箭迭代制导方法的改进研究[J]. 动力学与控制学报, 2009, 7(3) :279-282. [Wu Nan, Cheng Wen-ke, Wang Hua. An improved iterative guidance method for launch vehicle[J]. Journal of Dynamics and Control, 2009, 7(3) :279-282.]