一种用于非合作目标惯性指向轴位置捕获的绕飞方法

刘 涛，王 勇，解永春，胡锦昌

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点试验室,北京 100190)

0 引 言

随着人类航天活动的深入开展，对航天器在轨服务和空间碎片清理等任务的研究方兴未艾。在轨服务和空间碎片清理任务多需要对非合作航天器进行交会操作，所谓非合作航天器是指不能提供有效合作信息的航天器。为对非合作航天器进行详查或沿特定方向对其进行抵近操作，追踪航天器需要围绕非合作航天器进行绕飞机动。绕飞可分为基于相对运动特性的自然绕飞以及受控的快速绕飞[1], 根据绕飞过程中追踪航天器与目标航天器是否处于一个轨道平面，又可将绕飞运动分为共面绕飞和异面绕飞。由于受控快速绕飞的周期可控，绕飞面可任意设计，所以更适用于在轨服务等任务。Straight[2]和Yoshihiro等[3]研究了近圆多脉冲快速绕飞，通过等时间间隔施加脉冲，使追踪航天器在圆形相对轨道上环绕目标航天器。Hari等[4]提出了滑移制导方法，采用直线进行接近轨道规划，通过多脉冲控制逐渐靠近轨道系中的目标位置。张庆展等[5]研究了航天器任意方位的快速绕飞与视线指向的建模与控制问题。王功波等[6]给出了连续小推力条件下的一种快速圆编队设计方法。杨乐平等[7]基于CW方程，针对绕飞观测任务，讨论了数种可用的自然绕飞轨迹设计方法。谭天乐[8]则针对大椭圆轨道航天器相对控制问题，采用幂级数法对系统相对动力学方程进行了近似求解，并设计了状态反馈制导律用于航天器循迹绕飞的控制。此外，谭天乐还针对一般轨道航天器相对运动问题，直接求解相对运动解析解，以获得相对状态的预期偏差。通过广义逆变换构造关于预期偏差的全状态反馈控制器，形成一套可用于绕飞控制的相对制导律[9]。

目前，多数绕飞问题均在目标航天器轨道系中进行讨论，控制目标为形成特殊的绕飞轨道或捕获轨道系中的某一目标位置。实施空间碎片抓捕等非合作目标交会任务时，必须首先明确非合作目标的姿态运动规律以及外形特征，即需要对非合作目标航天器进行近距离详查。无控非合作目标航天器的姿态运动比较复杂，但其姿态角动量矢量保持惯性定向，采用角动量矢量指向为基准可清晰描述姿态运动。因此，追踪航天器可通过捕获非合作目标航天器在惯性空间某一指向轴(如角动量矢量方向)上的目标位置，并对目标进行持续观测以获得相关参数，必要时还可沿该惯性指向抵近目标并进行抓捕等操作。近圆轨道近距离相对位置控制多基于CW制导进行设计，而CW方程在轨道系中描述相对运动。与捕获轨道系中的位置点不同，惯性空间轴上的位置在轨道系中是变化的。若采用直线接近方式接近目标位置，接近过程中追踪航天器可能会距离目标航天器过近而存在轨迹安全性隐患，为此需要对接近轨迹进行特殊设计以确保轨迹安全。

本文提出一种适用于非合作目标惯性指向轴位置捕获任务的绕飞控制方法。该方法依据初始相对位置和目标位置确定绕飞坐标系；在绕飞坐标系中，为确保接近过程的轨迹安全，分别采用扇形和直线方式设计了两类接近轨迹规划策略。通过计算制导时刻追踪航天器与目标位置间的夹角，大角度时采用扇形接近轨迹规划策略，小角度时采用直线接近轨迹规划策略，规划得到过渡目标位置，并采用CW制导进行过渡目标位置的接近控制，进而逐渐接近目标位置；在交会过程中，为保持相对测量敏感器始终有效测量，还设计了姿态指向控制律使追踪航天器本体x轴始终指向目标。

论文中主要涉及惯性J2000.O系、RVD系和绕飞系共三种坐标系，坐标系原点均为目标航天器质心，通过上标区别不同坐标系中的矢量坐标，依次标记为ri，rr，rf,而矢量表示的下标用于标识矢量的具体物理含义。

1 基于CW制导的相对轨道控制

近地轨道目标航天器多运行于近圆轨道。以目标航天器轨道系作为参考系，在相对距离远小于轨道高度时，可采用CW方程描述追踪航天器相对目标航天器的轨道运动。

首先定义相对运动坐标系Or-xyz(RVD坐标系)：其原点Or为目标航天器的质心，z轴指向地心，y轴垂直于z轴，指向轨道角速度方向，x轴与z轴和y轴构成右手系。

在RVD系中，CW方程的具体形式为[7]：

(1)

式中:ωt为目标航天器轨道角速度，ui(i=x,y,z)为三轴加速度。

以相对位置和相对速度为状态量

其中,Xr表示相对位置，Xv表示相对速度。由于CW方程为线性定常系统，可以求解得到转移方程为

(2)

式中：

Φrv(t,t0)=

φ=ωt(t-t0)

在针对近圆轨道目标航天器的相对轨道控制任务中，普遍采用基于CW方程的CW制导作为近距离交会的轨道控制策略。已知当前相对状态X(t0),目标位置XT,转移时间Δt时，CW制导描述为：

Φrr(t0+Δt,t0)Xr(t0))

(3)

(4)

2 绕飞任务

整个绕飞任务分为捕获惯性指向轴目标位置绕飞、位置保持控制、返回RVD系保持点绕飞和绕飞阶段姿态指向控制等四方面进行设计。

3 捕获惯性指向轴目标位置绕飞

3.1 确定绕飞坐标系

(5)

RVD系到绕飞坐标系的姿态阵为：

(6)

式中:Ci(·),i=x,y,z表示绕i轴定轴转动得到的姿态阵。

3.2 规划过渡目标位置

将当前位置和目标位置转换到绕飞系中：

(7)

(8)

(a)扇形接近轨迹规划

首先，设定绕飞平均角速度为ωf=π/tπ(rad·s-1)，tπ为绕飞相位角为180°时的设计时长，通常可选为0.1～0.5个轨道周期，本文设定为0.3个轨道周期。进而得到本次绕飞的总时长Δtf=θf/ωf。

规划得到的过渡目标位置为：

(9)

(b)直线形接近轨迹规划

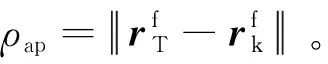
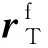
若需要采用指数函数对接近过程中的相对距离进行规划时，设定接近过程中的相对距离满足ρ(t)=ρkeaapt，其中aap为时间常数，依据终端条件进行确定，即aap=ln(ρT/ρk)/Δtf。可得过渡目标位置的相对距离为ρTk=ρkeaapΔtfk，对应的转移时间为Δtfk=δρ/vap，进而求解过渡目标位置

(10)

其中，Δρ按照下式计算：

(11)

Δρ需要满足0<Δρ≤ρap。此外，当ρT与ρk接近时，会使由式(11)得到的Δρ过小。为确保接近进程的快速性，若Δρ<δρ，则取Δρ=δρ。

(c)确定过渡目标位置

完成(a)或(b)的规划设计后，将规划得到的绕飞系中的过渡目标位置转换到RVD系中

(12)

(13)

其中，Cr,i(t)为t时刻惯性系到RVD系的姿态阵，可由目标器定轨结果得到。

3.3 制导计算

Φrr(tk+Δtfk,tk)Xr(tk))

(14)

进而可以确定需要施加的速度增量为：

(15)

4 位置保持

由于惯性指向轴上的目标位置在RVD系中是变化的，所以追踪航天器在绕飞过程中需要实时依据相对状态导航值进行判断。当接近目标位置时，自主转入位置保持。为进行位置保持控制，首先计算目标位置在当前RVD系中的坐标：

(16)

依据当前相对状态求解与目标位置的误差：

(17)

采用双积分模型对三轴相对位置运动进行近似描述，则可以采用相平面控制或PID控制进行位置保持控制律设计。本文采用相平面控制进行控制器设计[10]，相关设计参数见表1。

表1 位置保持控制相平面参数Table 1 The phase plane parameters for relative position holding

表1中，KX为抛物线斜率参数。三轴参数相同。

5 返回RVD系保持点绕飞

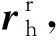
6 绕飞阶段姿态指向控制

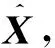
(18)

(19)

据此，追踪航天器本体系到目标指向坐标系的姿态阵为

(20)

再根据惯性姿态Cbc,i，得到惯性系到目标指向系的姿态阵为CT,i=CT,bcCbc,i。

采用姿态误差四元数计算控制参数，即：

(21)

其中，四元数乘法的定义见文献[11]。将俯仰和偏航轴姿态控制到0即可保证本体+x轴指向目标，进而得到俯仰和偏航轴姿态控制参数：

(22)

(23)

其中，qbc,T(2)表示qbc,T的第2个元素。滚动轴作为指向轴，该轴的控制目的为消除不必要的自旋转动，故滚动轴姿态采用角速度阻尼方式进行设计，具体控制参数为

(24)

式中:Δt为控制周期，ωbc,i为追踪航天器的惯性角速度。

采用PID+PWM喷气控制进行姿态指向控制器设计[12]。

7 数学仿真

表2 目标航天器的初始轨道Table 2 The initial orbit elements of target spacecraft

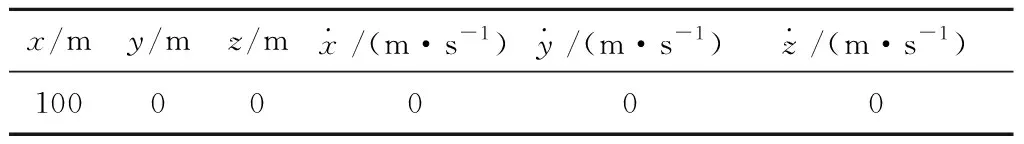
表3 初始RVD系相对状态Table 3 The initial relative states in RVD frame

态动力学采用刚体转动动力学模型。

仿真结果见图2～图9。由图2和图3可知，惯性轴目标位置捕获绕飞中，由于初始夹角大，所以第1～6过渡目标位置均采用扇形方式进行规划得到，仅第7过渡目标位置采用了直线方式进行规划，并且整个绕飞过程中相对距离始终大于20 m(见图8)，这确保了绕飞轨迹的安全性；图5和图6表明惯性轴目标位置保持控制中，追踪航天器始终能够跟踪RVD系中变化的目标位置；图7表明返回绕飞控制中，第1个过渡目标位置采用了扇形规划方式，其余5个过渡目标位置由于夹角较小均采用了直线规划方式，且绕飞过程中的相对距离也始终大于20 m(见图8)；由图8可知，整个任务中，两航天器间相对距离始终大于20 m且相对距离变化平滑，表明采用指数函数进行相对距离规划的良好性能。而α和β角均小于1°，表明激光雷达光轴始终精确指向目标，追踪航天器本体角度速也较小(见图9)，表明姿态指向控制的优良性能。最后，表4和表5给出了目标捕获绕飞过程和返回保持点绕飞过程中，位置控制速度增量分别为0.829 (m/s)和0.380 (m/s)，合计为1.209 (m/s)。

表4 惯性轴位置捕获绕飞各次制导脉冲(RVD系)Table 4 The guidance impulses of fly-around to capture the position on inertial axis in RVD frame

表5 返回保持点绕飞各次制导脉冲(RVD系)Table 5 The guidance impulses of fly-around to holding position in RVD frame

8 结束语

在轨服务和空间碎片清理等任务多需要对非合作航天器进行交会操作。为对非合作航天器进行详查、沿特定方向抵近目标，往往需要追踪航天器捕获非合作航天器在惯性空间某一指向轴上的目标位置。本文提出一种适用于非合作目标惯性指向轴位置捕获任务的绕飞控制方法。该方法分别采用扇形和直线方式设计了两类接近轨迹规划策略，依追踪航天器与目标位置间的夹角选择具体的接近轨迹规划策略，规划得到过渡目标位置，并采用CW制导进行过渡目标位置的接近控制，逐渐接近目标位置；在交会过程中，还设计了姿态指向控制律使追踪航天器x轴始终指向非合作目标。本文所提出的方法对实际工程设计具有参考价值。

参 考 文 献

[1] 邬树楠.接近空间目标的追踪航天器控制方法研究[D].哈尔滨:哈尔滨工业大学,2012.[Wu Shu-nan. Research on control of chaser spacecraft with proximity to space target[D]. Harbin：Harbin Institute of Technology，2013.]

[2] Straight S D. Maneuver design for fast satellite circumnavigation[D].Ohio:Air Force Institute of Technology, 2004:1-5.

[3] Yoshihiro I, Akira I. Optimal impulsive relative orbit transfer along a circular orbit[J].Journal of Guidance, Control, and Dynamics, 2008,31(4): 1014-1027.

[4] Hari B H, Myron T, David D B. Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular orbit[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, Canada, 2001.

[5] 张庆展,曾占魁,靳永强,等.空间快速绕飞与视线指向的建模与控制[J].宇航学报,2014,35(3):324-330. [Zhang Qing-zhan,Zeng Zhan-kui,Jin Yong-qiang,et al. Modeling and control on fast fly-around and line of sight pointing[J]. Journal of Astronautics, 2014,35(3):324-330.]

[6] 王功波,孟云鹤,郑伟,等.快速绕飞卫星空间圆编队设计方法[J].宇航学报,2010,31(11):2465-2470.[Wang Gong-bo,Meng Yun-he,Zheng Wei,et al. Fast fly around satellite space circle formation design[J]. Journal of Astronautics, 2010,31(11):2465-2470.]

[7] 杨乐平,朱彦伟,黄焕.航天器相对运动轨迹规划与控制[M].北京：国防工业出版社,2010:185．

[8] 谭天乐.椭圆轨道交会、悬停与绕飞的全状态反馈控制[J].宇航学报,2016,37(7):811-818.[Tan Tian-1e. Full state feedback control of rendezvous，hovering and fly-around in elliptical orbit[J]. Journal of Astronautics,2016,37(7):811-818.]

[9] 谭天乐,武海雷. 轨道交会、悬停及绕飞控制的解析解方法[J].宇航学报,2016,37(11):1333-1341.[Tan Tian-1e,Wu Hai-lei. Analytical solution method for orbit rendezvous，hovering and fly-around control[J]. Journal of Astronautics, 2016,37(11):1333-1341.]

[10] 周建平.空间交会对接技术[M].北京：国防工业出版社,2013:192-197.

[11] 章仁为.卫星轨道姿态动力学与控制[M]. 北京:北京航空航天大学出版社, 1998:145-147.

[12] 王寨,李铁寿,王大轶.探月卫星变轨时的姿态控制研究[J].航天控制,2005,23(1):11-14.[Wang Zhai,Li Tie-shou,Wang Da-yi.Attitude control during lunar satellite orbit maneuver[J].Aerospace Control,2005,23(1):11-14.]