初中学生在不等式部分的学习问题探究

汪秀云

(福建省南平市浦城县仙阳中学 353409)

不等式部分内容是初中数学教学的重要组成部分，也是初中数学的教学难点，很多学生在学习中存在诸多问题，一是因为该部分知识本身难度所致，还有一方面是学生首次接触不等式，在解题方法和知识理解上有所欠缺，这些都导致了初中生在不等式部分学习困难的情况.

一、初中生不等式部分知识学习维度

1.记忆学习维度

记忆是学生学生学习的基础，通过该维度的学习，学生能够对不等式的概念、不等式的关系和不等式的性质进行记忆，能够知道不等式符号的改变条件.能够达到这一学习维度的学生，一部分学生能够解决一些不需要推理的问题，能够借助不等式的定义来求解问题，如例1之类的问题.还有一部分学生能够解决一些关于不等式程序性记忆要求较高的问题，这类问题不需要过多的推理，只要通过去分母、移项就可以完成求解，如例2之类的问题.

例1：从下列式子中挑选出不等式：-5x<0;5x+5>0;x=-8;y≠8;x-7≥0.

对于这样的问题只需要根据不等式的定义，一个一个往里套就可以，只要不符合条件要求的都可以舍去.

例2 解不等式：2x-2≥4x.

2.解释学习维度

3.探究学习维度

探究性学习是学生学习达到一定高度，能够解决一些非常规的问题，能够对某一数学问题进行创造和改造，创造性的解决某一数学问题.首先，能够从问题背景中找出蕴含的数学不等式关系，找出解题的突破口.其次，能够根据题目信息，建立不等式模型.例如，某服装厂有甲布料38米、乙布料26米，打算用这些布料制作A、B两款衣服，其中A款衣服需要甲布料0.5米，乙布料1米，可以产生45元的利润；B款衣服需要甲布料0.9米，乙布料0.2米，可以产生30元的利润；其中生产A款衣服的数量为x，两种款式获得的总利润为y.

(1)写出x、y的关系方程，并写出x的取值范围.

(2)该批次需要生产多少A款的衣服才能够使的服装厂的利润最大化？最大利润是多少？

干预前两组心理状态评分均差异无统计学意义（P>0.05），干预后观察组的HAMA与HAMD评分均显著低于对照组（P＜0.05），见表 2。

这个问题从本质上来说就是一个建立函数模型、解决函数模型的过程.

二、初中生不等式部分学习存在的问题

1.不等式关系方面

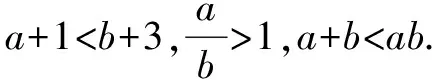
2.不等式性质方面

不等式的性质主要包括三个方面，第一，在不等式两侧都加上或者减去同一个整式，不等式的不等号方向不变；第二，在不等式两侧同时乘以或者除以一个正数，不等式的不等号方向不变；第三，在不等式两侧同时乘以或者除以一个负数，不等式的不等号方向改变.通过学生在平时的练习发现，学生对于该部分知识的掌握相对较好，仅有极少数学生对该部分知识掌握存在问题，由此可见，该部分知识难度相对较低.从存在的问题来看，这极少数的学生对不等式性质的理解不够透彻，仅仅停留在不等式的基本性质的记忆上，对于等式的性质和不等式之间的性质不能够灵活转化，知识的迁移能力较差.例如下列练习题：

下列不等式变形的依据是：

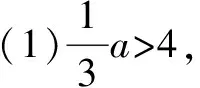
(2)a-9>0,得出a>9

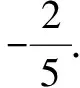
例：如果a

在证明B不等式的时候，学生往往只顾着两侧乘以b去约分，忘了b<0这一先决条件，导致出错，证明C存在的问题和B一样，都忽视了字母中隐含的符号关系.

3.不等式解集方面

在这一方面，学生存在的主要问题就是对“一个解”、“唯一解”、“解集”、“解”的把握不准确.尤其是在“解”和“解集”的概念上，没有把握好.造成这一因素的主要原因就是学生对这些概念把握不到位，另外，不等式的解与方程的解相类似，学生没有准确的把握两者之间的区别，这才导致了错误的产生.

4.不等式组方面

涉及到该部分知识的问题，一般情况下对学生的计算能力要求较高，在平时的练习中，出现问题的学生主要是计算错误.有的学生在移项的时候没有改变不等号的方向，还有些学生就是对不等式性质把握不当，应用过程中出现问题.

例如：解下列不等式组，并在数轴上表示出来.

5.一元一次不等式和一次函数方面

通过对学生平时的练习可以看出，学生对于该部分不等式的求解更偏向于运用代数的思维来做，尽管有些问题只需要通过函数图像就可以明显的看出，学生依然选择复杂的代数法.如果学生采用函数图像的方法来求解，就需要仔细认真，尤其是在符号变化上要注意.相比较于函数图像法来求解，代数法不涉及到不等号的变换问题，学生出错的几率更低一些.

例1 一次函数y=2x-4交x轴与(2，0)一点，那么一元一次不等式y≤0的解集是？

A.x≤2 B.x<2

C.x≥2 D.x>2

在利用函数图像法解这一题的时候，部分学生在将坐标系中y<0时，x的取值范围转化为代数时出现错误，图像中的解集是x≤2,当换成代数时不等号的方向却反了.

初中学生对于不等式部分知识的学习可以分为三个理解水平，学生的记忆和解释学习水平较高，但是探究性学习水平较低，导致学生在解决常规性问题的时候能够游刃有余，一旦涉及到创新性问题就不知从何下手.另外，学生在不等式部分的学习中经常存在迁移错误、表征错误和取之错误的问题，这些问题涵盖了不等式部分的所有内容，需要教师在教学中加以重视.

参考文献：

[1]彭明菊.关注过程·丰富经验·提升品质——以“不等式的概念”教学为例[J].新教育,2014(02):51-52.

[2]闫建明.浅谈关于方程(组)、不等式(组)、函数等初中数学模型的教学及应用[J].新课程学习(中),2013(04):46-47.