三维波浪作用下钢吊箱围堰下放过程受力研究

黄 博, 段伦良, 祝 兵

(西南交通大学土木工程学院, 四川 成都 610031)

随着大型跨海桥梁工程的蓬勃发展,钢吊箱围堰在修筑深水承台中得到了广泛的运用.复杂的海洋环境对跨海桥梁钢吊箱围堰的准确定位以及下放安全性带来了巨大的挑战.近年来,国内外学者对钢吊箱围堰进行了大量研究.文献[1]中基于文氏谱以及线性谐波叠加法完成了波浪频谱与波浪时程的转换,得到了钢吊箱的动力响应,通过动力分析结果与特征波法、规范静力法对比,建议在波浪荷载作用下,动力分析结果应在静力计算结果基础上乘以一个放大系数.文献[2]中针对地震作用下钢吊箱结构进行了响应谱分析,结果表明钢吊箱在地震作用下位移和应力均较小,验证了其安全可靠性.文献[3]中分析了钢吊箱在风荷载作用下的动力响应,得出钢吊箱在脉动风压对结构动力响应的影响较小的结论.文献[4]中针对围堰所受的残余空隙压力进行了数值模拟,对长期波浪作用下围堰稳定性以及围堰支撑结构的设计进行了改善和优化.文献[5]中等研究了波浪作用下不同吃水深度的圆端形吊箱围堰所受波浪力的作用,结果表明，圆端形吊箱围堰随着吃水深度的增加,围堰所受纵向力呈上升的趋势、垂向波浪力减小.目前,钢吊箱围堰的研究主要是针对其结构动力特性.在跨海大桥建设中,波浪荷载已经成为决定钢吊箱围堰施工安全性的主要荷载,波浪荷载对桥梁结构作用的研究[6-12]较多,而在围堰下放过程中所受波浪荷载的相关研究较为缺乏.本文研究不仅考虑了围堰动态下放过程对所受波浪力影响,同时也考虑了钢护筒的存在对周围波浪场的影响,与以往研究处于不同淹没深度时单纯围堰波浪力计算相比,更符合工程实际.

文中通过建立钢吊箱围堰下放过程中波浪与围堰相互作用的三维数值模型,以某座在建的跨海桥梁3#墩施工所采用的哑铃型钢吊箱围堰为背景,研究了处于下放过程的钢吊箱围堰周围波浪场的变化、围堰受力与处于固定淹没深度处围堰受力的比较以及不同波浪特性对下放过程的钢吊箱哑铃型围堰受力的影响.

1 数值模型

基于CFD软件通过求解RANS方程和k-ε方程建立三维数值波浪-围堰相互作用模型,采用VOF(volume of fluid)流体体积法捕捉自由液面.模型建立过程中,钢吊箱围堰尺寸参照某在建跨海大桥3#墩哑铃型钢吊箱围堰,详细尺寸如图1所示.

图1 围堰几何尺寸(单位:m)Fig.1 Dimensions of the cofferdam (unit: m)

图1中：L为围堰长度；B为围堰宽度.哑铃型钢吊箱围堰下放施工过程:首先在预定位置打下钢护筒,然后在钢护筒上设置吊挂牛腿来吊装围堰进而控制围堰的下放,在钢护筒与围堰之间通过钢架连接.整个围堰下放过程始终处于控制之中,假设围堰在下放过程中始终是做匀速运动,淹没深度为0≤h≤12.88 m.由于钢护筒与围堰之间具有可靠连接,围堰与钢护筒是一个整体,下放过程中受波浪力作用时的位移较小,将钢吊箱围堰作为刚体做匀速下放运动.图2为波浪-围堰相互作用的数值模型计算域布置.围堰在波浪作用时间内匀速下放直到最终淹没深度，其中：L=84.8 m；B=37.8 m；水深d=26.5 m；围堰高度h0=16 m.

1.1 数学模型

对于不可压缩三维波浪模型,流体运动的控制方程主要包括连续性方程和动力方程,由于CFD软件采用FAVOR网格处理技术,其控制方程中加入了面积分数和体积分数,具体形式为

(1)

(2)

(3)

(4)

式中:ux、uy、uz分别为x、y和z方向的速度;Ax、Ay、Az分别为x、y和z方向可流动的面积;VF为可流动的体积分数;ρ为水密度;Gx、Gy、Gz分别为x、y和z方向的重力加速度;fx、fy、fz分别为x、y和z方向的粘滞力加速度.

(a) 计算域布置

(b) 三维数值水槽布置图2 波浪-围堰相互作用Fig.2 Sketch of wave-cofferdam interactions

选用k-ε模型实现湍流封闭,引入面积参数和体积参数后的k-ε方程为

PT+GT+DT-εT,

(5)

(6)

式中：kT为紊动能;εT为紊动耗散率;PT为速度梯度引起的湍动能k的产生项;GT为由浮力所产生的紊动动能的产生项;C1、C2、C3为修正系数，C1=1.44，C2=1.92，C3=0.20.

基于CFD软件利用速度入口法建立三维波浪模型,坐标轴取波浪传播方向为x轴,垂直于波浪传播方向为y轴,水深方向(垂向)为z轴.数值水槽边界条件设为:入口边界处输入流速条件;出口边界设置出流条件,且在出口边界之前设置消波区[13],防止波浪在边界处发生反射;自由液面处波浪压力相对值为0,采用VOF法捕捉自由液面[14];前后为对称边界,边界处各物理量的相对梯度为0,使数值水槽侧向的宽度不会对数值模拟结果准确性产生影响;底部及结构物表面采用固壁边界.

2 模型验证

本文在数值模型验证部分首先进行波浪传播稳定性验证,然后将本文结构物模型替换成大型圆柱,进行数值模拟与实验结果对比验证,最后进行模型网格收敛性验证.

图3给出了无结构物时数值波浪水槽造波以及波浪传播效果图,此时，波高H=2 m,周期T=6 s，Stokes 5阶波浪在800 m区域内传播到30 s时的波面，图中：xw为水槽在x方向各点位置；Hw为30 s 时对应于每个点的波面高程.

图3 30 s时波面图Fig.3 Water surface at 30 s during wave transportation

由图3可以看出,在波浪传播过程中,数值水槽中波浪传播稳定,且在消波区范围内消波效果显著,能有效避免波浪在边界处发生反射.

为验证本文模型对结构物所受波浪力模拟的准确性,采用本文数值水槽模型模拟波浪作用下固定竖直截断圆柱所受的波浪力,并与文献[15]的波流水槽内进行竖直截断圆柱受波浪力作用的物理实验结果进行对比验证.

实验水槽长宽高分别为69.0、2.0、1.8 m,水深为1.0 m,圆柱半径为15. 0 cm, 淹没深度为50.0 cm,圆柱模型距离造波机30.0 m,圆柱上端连接测力天平,当圆柱处入射波稳定后,进行采样,反射波到达圆柱之前完成采样.本文进行了6种工况的数值模拟,实验结果与数值计算结果对比如表1所示，表中：a为圆柱半径；g为重力加速度；A1为波幅；Fx为水平波浪力；Fy为竖直波浪力.

由表1可以看出,数值计算结果与实验结果吻合较好,说明本文建立的数值模型可以有效的计算结构物在波浪场中所受的波浪力.

表1 数值计算结果与实验结果的比较Tab.1 Comparison between numerical results and experimental data kN

图4给出了不同网格尺寸比例下围堰下放过程中所受水平波浪力最大值的变化.验证过程中相关参数取值如下:d=26.5 m；H=4 m,T=8 s,数值水槽长宽高分别为800、300、50 m,哑铃型围堰中心放置在x=400 m、y=150 m处.从图4可以看出，本文模型网格密度选择合理.

图5为本文所采用的数值模型y-z平面的网格划分.

图4 不同网格尺寸比例对应的最大水平波浪力Fig.4 Variations of horizontal wave force versus different meshsizes

图5 数值模型y-z平面的网格划分Fig.5 Sketch of mesh generation for the y-z plane of the numerical model

3 工程应用

基于上述模型进一步研究处于下放过程的哑铃型围堰受力变化情况以及不同波浪特性对下放过程的钢吊箱哑铃型围堰受力的影响.围堰在整个波浪作用过程中匀速下放,淹没深度取值为0≤h≤12.88 m,波浪采用Stokes5阶波.模型网格采用图4中所示网格尺寸,时间步长取值为0.01 s.

3.1 围堰下放过程中周围波浪场的变化

图6给出了钢吊箱围堰下放过程中,波浪压力场在1个周期内的变化,H=4 m,T=8 s，图中，t为围堰下放时间；t0为钢吊箱围堰下放的初始时间.

由图6(a)可以看出，围堰在下放过程中会造成周围波浪场的分布变化,因此，单纯研究处于固定淹没深度时围堰所受波浪力不够准确,考虑围堰在下放过程中所受波浪力才符合工程实际.

图6(b)可以看出，当围堰下放以及波浪与围堰相互作用共同导致波峰作用在围堰上时,在围堰迎浪侧会发生涌浪现象,且在哑铃型围堰中部以及围堰形状变化的地方,周围波浪容易发生破碎.

图6(c)和(d)所示,在波峰经过围堰之后,在围堰的背浪侧(哑铃型围堰尾部)由于围堰形状的影响,会产生波浪压力场变化相对较大的区域.

图7给出了围堰下放过程中某一时刻波浪场中流速矢量的分布.由图7中可以看出,由于围堰的下放产生的波动以及波浪作用在围堰迎浪侧而发生的反射波会在围堰前端与将要作用在围堰上的波浪发生相互作用,造成围堰前端波浪爬高和破碎以及贴近围堰表面的漩涡产生.由于哑铃型围堰形状的变化,会在围堰尾部产生漩涡,使得压力发生变化.

因此,在钢吊箱哑铃型围堰下放过程中,围堰迎浪侧需要进行适当的防护措施,防止波浪爬高及破碎的波浪荷载作用造成围堰的破坏,在围堰尾部形状变化较大的区域采取适当防护,避免漩涡产生压力差引起的破坏.

(a) t=t0(b) t=t0+T/4(c) t=t0+T/2(d) t=t0+3T/4图6 围堰周围波浪压力场随时间变化Fig.6 Variations of the wave pressure around the cofferdam over time

图7 围堰周围流速矢量分布Fig.7 Distributions of velocity around the cofferdam

3.2 围堰下放过程中所受波浪力的变化

在实际工程中,围堰拼装完成后会由钢护筒上的吊索下放到指定标高,在围堰下放过程中,由于围堰尺寸相对较大,波浪对围堰的作用力对围堰的下放的稳定性以及围堰结构的安全性影响较大,研究钢吊箱围堰下放过程中所受波浪力的变化情况对围堰的设计以及下放过程中的施工安排和防护措施具有较大的意义.本文基于此模型研究了钢吊箱哑铃型围堰下放过程中与处于固定深度时的围堰所受波浪力的进行对比.

图8给出了H=4 m、T=8 s、围堰以固定速度从h=0下放到h=12.88 m过程中围堰的受力及围堰处于h=6.44,12.88 m时围堰所受波浪力的变化.

由图8(a)可以看出，在围堰下放过程中第1个周期内所受水平力较小,此时围堰所受波浪力是由围堰下放引起的周围波浪场变化,进而产生的水平力,因此水平力较小.当波浪到达并作用在围堰上时,水平力剧增,此时随着围堰下降,波浪力在两个周期内变化不大,因为此时下放深度较浅,波浪部分作用在围堰上.随着围堰继续下放,在两个周期内,波浪全部作用在围堰上,波浪力增大.当围堰继续下放直到最终位置时,此时围堰淹没深度的较大,露出水面部分减少,围堰所受波浪力达到最大值.相比较于处于下放状态的围堰受力情况,围堰处于固定淹没深度时,其所受波浪力变化较为平缓,且由于固定围堰对周围波浪场的影响较小,计算所得水平波浪力与处于下放过程的围堰受力相比,最大波浪力值较小.因此,考虑下放过程中围堰所受波浪力更符合工程实际,所得计算结果更准确.

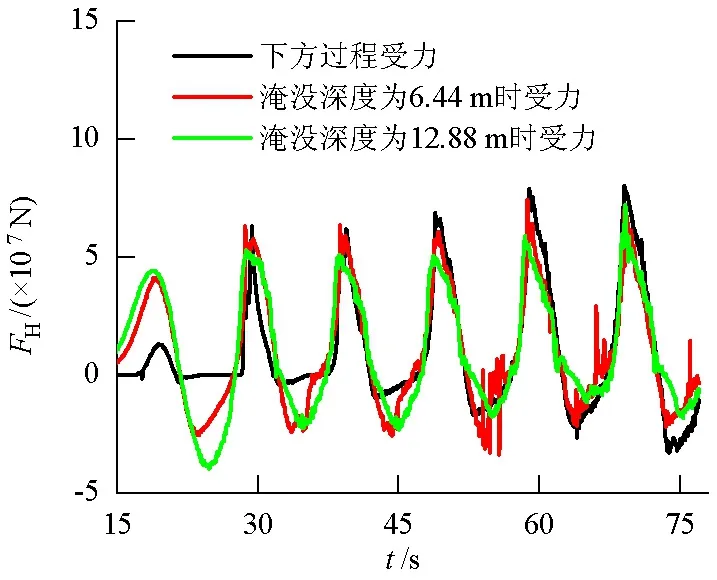
(a) 围堰所受水平力(FH)

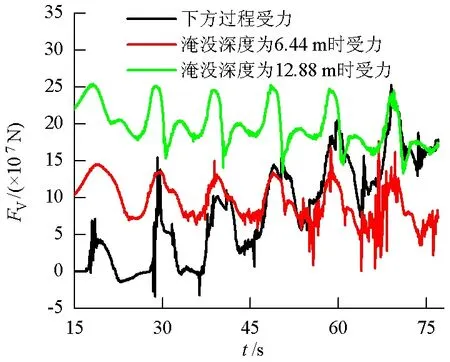
(b) 围堰所受竖直力(FV)图8 不同工况下钢吊箱围堰所受波浪力的变化Fig.8 Variations of wave forces on the steel-suspending-cofferdam under different conditions

综上所述,水平波浪力在围堰下放过程中会达到最大值,但在下放开始阶段,水平力存在一个突变的阶段,且考虑下放过程所得波浪力较固定深度围堰波浪力大10%.因此,施工过程中应考虑到围堰下放对水平力的影响以及水平力的突变所带来的围堰下放安全问题.

由图8(b)可以看出，竖直力随着围堰的下放是逐渐增大的,是符合实际情况的.围堰刚接触水面时,竖直力的负值可能是因为水表面张力的影响.随着围堰的下放,竖直力呈现增大的趋势,围堰和钢护筒的存在以及围堰下放对周围波浪的影响则会使竖直力的增大出现波动,并且在波谷处波动较明显.h=6.44 m的围堰由于淹没深度较小,其所受波浪力波动较大；h=12.88 m的围堰因淹没深度较大,波动较为稳定.

由图8(b)还可以看出，3个不同工况下波浪力曲线均在相应阶段有部分重合,说明计算结果准确.

综上所述,下放过程中围堰所受竖直波浪力变化剧烈程度介于两个不同淹没深度工况之间,计算结果更符合工程实际,对钢吊箱围堰施工控制更具有参考价值.同时,围堰下放过程中水平方向所受波浪力的数值变化以及竖直方向所受波浪力的波动所造成的下放精度和稳定性控制难度的增加是围堰设计和施工中重点需要关注的问题.

3.3 波浪特性对下放过程中围堰所受水平波浪力的影响

众所周知,波浪特性对结构物受力影响较大,波高直接影响作用于围堰表面的波浪压力,周期则通过影响波长和波速进一步影响围堰表面的波浪压力.本文研究了在围堰下放过程中所受波浪力的变化,基于此模型进一步探讨波浪特性对下放过程中钢吊箱哑铃型围堰所受波浪力的影响.

图9和图10分别为围堰所受最大水平力随波高的变化(T=8 s)和随周期的变化(H=4 m).由于此类钢吊箱围堰在竖直方向采用吊索进行下放,下放过程中水平波浪荷载对围堰下放稳定性和安全性影响较大,而水平波浪荷载中,则以围堰主迎浪面的波浪荷载为主(x方向).由于围堰迎浪面面积较大且是波浪直接作用面,相较于围堰侧面(y方向)受力较大.经过数值计算,迎浪面波浪荷载最大值约为侧向波浪荷载最大值的100倍.因此,此部分围堰所受水平波浪力的研究只涉及迎浪面波浪荷载(x方向).以上所采用的波浪特性值参考该围堰附近海域波浪特性实测统计值.

从图9中可以看出,在波浪周期及水深一定的情况下,随着波浪高度的增加,波浪能量的增大,围堰下放过程中所受最大水平力呈现逐渐增大的趋势,且当H>4.5 m时,水平力增幅变大.因此,根据围堰施工附近海域所测波浪参数情况,在大浪天气条件下,应避免围堰下放施工或在施工过程中采取相应防护措施,避免发生水平力过大所造成的围堰破坏,围堰内部钢护筒的破坏以及围堰下放稳定性安全问题.

从图10中可以看出,在波浪高度及水深一定的情况下,在一定范围内(T=6～8 s)随着波浪周期的增加,围堰下放过程中所受最大水平力呈现增大的趋势,但增大的幅度逐渐减小.因此,在钢吊箱围堰施工时,应考虑波高和周期两者共同对围堰下放中所受水平波浪力的影响.

图9 围堰所受最大水平力随波高变化Fig.9 Variations of maximum horizontal wave force on cofferdam versus wave heights

图10 围堰所受最大水平力随周期的变Fig.10 Variations of maximum horizontal wave force on cofferdam versus wave periods

4 结 论

本文基于CFD软件建立了三维波浪下钢吊箱哑铃型围堰下放过程的模型,通过此模型分别研究了钢吊箱围堰下放过程中周围波浪场的变化、围堰下放过程中所受波浪力的变化以及波浪特性对下方中的围堰所受水平波浪力的影响,根据本文研究结果,得到如下结论：

(1) 本文所建立的数值模型准确可靠,可据此分析钢吊箱围堰下放过程中波浪场的变化以及围堰下放过程中波浪与围堰相互作用.

(2) 围堰和钢护筒的存在以及围堰下放过程均会对周围波浪场产生显著的影响;围堰前端以及尾部波浪场变化较大,是围堰结构破坏最容易产生的部位.

(3) 考虑围堰下放过程所得的波浪力较固定淹没深度的围堰所受波浪力更为准确,更加符合工程实际.施工过程中应考虑到围堰下放对水平力的影响以及水平力的突变所带来的围堰下放安全问题.同时,围堰下放过程中竖直力的波动所造成的下放精度和稳定性控制难度的增加也是围堰设计和施工中重点需要关注的问题.

(4) 随着波浪高度和波浪周期的增大,围堰在下放过程中所受最大水平力呈现增大的趋势,但随着周期的增大,水平力增大幅度逐渐减小.

[1] 徐伟,徐赞云,吴佳云. 随机波浪力下超大型钢吊箱围堰动力响应分析[J]. 沈阳工业大学学报,2012,34(4): 461-468.

XU Wei, XU Zanyun, WU Jiayun. Dynamic response analysis on ultra-large steel suspension box cofferdam under random wave force[J]. Journal of Shenyang University of Technology, 2010, 34(4): 461-468.

[2] 谢小松,徐伟,宋灿,等. 深水高桩承台哑铃状钢吊箱在地震作用下的响应分析[J]. 结构工程师,2005, 21(6): 43-45.

XIE Xiaosong, XU Wei, SONG Can, et al. Responseanalysis of elevated pile foundation dumbbell-shapesteel suspending cofferdam in deep water under seismicaction[J]. Structural Engineers, 2005, 21(6): 43-45.

[3] 徐伟,宋灿,骆艳斌,等. 深水高桩承台钢吊箱在风荷载作用下的动力性能分析[J]. 工业建筑,2007,37(7): 82-84.

XU Wei, SONG Can, LUO Yanbin, et al. Analysisof dynamic property of elevated pile foundation steelsuspending cofferdam in deep water under wind load[J]. Industrial Construction, 2007, 37(7): 82-84.

[4] XU Fei, LI Shucai, ZHANG Qianqing, et al. Analysis and design implications on stability of cofferdam subjected to water wave action[J]. Marine Georesources & Geotechnology, 2016， 34: 181-187.

[5] 祝兵,康啊真,邢帆,等. 三维波浪与圆端形吊箱围堰相互作用的数值模拟[J]. 桥梁建设,2013,43(6): 82-87.

ZHU Bing, KANG Azhen, XING Fan, et al. Numerical simulation of interaction between three-dimensional wave and round-end boxed cofferdam[J]. Bridge Construction, 2013, 43(6): 82-87.

[6] 方庆贺. 跨海近岸桥梁极端波浪作用研究[D]. 哈尔滨:哈尔滨工业大学,2012.

[7] 康啊真,祝兵,邢帆. 基于坐标和IBM的大型圆柱波浪力数值模拟[J]. 西南交通大学学报,2014,49(2): 233-239.

KANG Azhen, ZHU Bing, XING Fan. Numerical simulation of wave force on large circular cylinder based on coordinate and immersed boundary method[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 233-239.

[8] 刘浪,杨万理,李乔. 深水桥梁墩水耦合抗震分析方法研究[J]. 西南交大学报,2015,50(3): 449-453.

LIU Lang, YANG Wanli, LI Qiao. Seismic analysis method of deep-water bridge pier and water coupling[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 449-453.

[9] 陶建华,刘连武. 波浪和水流对大直径圆柱的共同作用力[J]. 水动力学研究与进展,1993,8(3): 265-272.

TAO Jianhua, LIU Lianwu. Wave-current forces on alarge vertical cylinder[J].Journal of Hydrodynamics,1993, 8(3): 265-272.

[10] GHAMRY E I. Wave forces on a dock[R].Berkeley： University of California, Hydraulic Engineering Laboratory, 2006.

[11] DOUGLASS S L, CHEN Q, OLSEN J M, et al. Wave forces on bridge decks[R]. Washington D. C.: Federal Highway Administration, Office of Bridge Technology, 2006.

[12] XIAO H, HUANG W, TAO J, et al. Numerical modeling of wave-current forces acting on horizontal cylinder of marine structures by VOF method[J]. Ocean Engineering, 2013, 67(3): 58-67.

[13] LARSEN J, DANCY H. Open boundaries in short wave simulations-a new approach[J]. Coast Eng., 1983, 7(3), 85-97.

[14] HIRT C W, NICHOLSB D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. J. Comput. Phys., 1981, 39: 201-225.

[15] 赵海涛,滕斌,李广伟,等. 竖直截断圆柱一阶波浪力的实验研究[J]. 中国海洋平台,2003,18(4): 12-17.

ZHAO Haitao, TENG Bin, LI Guangwei, et al. An Experimental study of first-harmonic wave force on vertical truncated cylinder[J]. China Offshore Platform, 2003, 18(4): 12-17.