基于温度比拟法的隧道衬砌水压精细化模拟分析
2018-06-01邹育麟
邱 月, 何 川, 何 聪, 邹育麟, 胡 炜
(1. 西南交通大学交通隧道工程教育部重点实验室, 四川 成都 610031; 2. 中铁二院工程集团有限责任公司, 四川 成都 610031; 3. 四川省铁路产业投资集团有限责任公司, 四川 成都 610031)
近些年,随着山区路网的丰富和完善,穿越高压富水地区的隧道不断增多,“以堵为主,限量排放(堵水限排)”的设计理念逐渐被接受和广泛使用[1],如何确定衬砌外水压力成为影响隧道施工与运营安全的关键[2].目前,计算衬砌外水压力的方法主要有折减系数法、理论解析法以及数值分析方法等[3-5].折减系数法主要用于水工隧道,在交通隧道中局限性较大[6];理论解析法一般针对环状(或等效后为环状)的结构体系进行计算,大多用于衬砌外水压力的简单二维平面问题分析[7];数值分析法目前应用最为广泛,但考虑流固耦合效应时,计算用时较长.
为提高计算效率,本文采用基于ANSYS热分析模块的温度比拟法,通过温度场模拟单一渗流场,在不考虑流固耦合效应的情况下,实现了衬砌水压的快速计算.文献[8-9]中分析了温度场与渗流场的基本理论、微分方程、初始条件和边界条件的相似性,为该法求解渗流问题提供了依据,并通过对土坝渗流问题的求解,证明了该法可以解决复杂边界、多种介质的渗流问题;文献[10]中提出现有较为成熟的渗流分析软件由于缺少用户自定义参数化语言,不能二次编程,导致渗流参数的调整设计和反分析有很大的限制和不便,而ANSYS的参数化设计语言(APDL, ANSYS parametric design language)则能为此提供有力的工具;文献[6,11]中大量计算得出温度比拟法与FLAC3D流固耦合分析法的计算误差在15%以内,能够满足工程需要.
隧道衬砌水压的计算,采用退化的轴对称解相对简单,较为常用.然而,温度比拟法与轴对称解的计算误差几何,能否在精细化的数值计算中有效应用都尚不明确.因此,本文分别使用温度比拟法、轴对称解和流固耦合法计算隧道在开挖未支护、施作衬砌以及围岩注浆3种工况下衬砌外水压力的分布规律,对比其计算误差,验证比拟法的可行性;同时,对高速公路典型双车道马蹄形断面建立围岩-注浆圈-防排水系统三维精细化模型,研究衬砌外水压力在隧道横断面和纵断面上的分布规律,并采用相同边界条件下的FLAC3D流固耦合分析法计算验证.
1 温度比拟法的实现
由于渗流场与温度场在物理特性、基础理论、初始条件、微分控制方程以及两类边界条件上均有高度的相似性,如果把对应的参数进行等值替换,渗流场和温度场则可以相应的转换,即渗流计算可以用温度比拟法替代完成[8,12].但该法不能与围岩、结构应力进行耦合分析,若只针对水压的计算问题,则具有较强的替代性.
采用温度比拟法进行渗流场计算分析时,需对计算做以下假设:
(1) 假设隧道围岩为均质、连续、各项同性介质,不考虑地层构造应力;
(2) 渗流属于恒定流且满足达西定律;
(3) 地下水位恒定,不因隧道开挖排水、排水管排水而改变.
2 验证温度比拟法的精度
由于渗流场的控制方程与温度场相同,且ANSYS的热分析模块以该理论为基础,因而,温度比拟法可视为一种偏微分方程的数值解法,在理论层面上,使用温度场的计算功能来实现渗流场计算是可行的.但考虑到有限元分析软件并非直接求解偏微分方程获取计算结果,而是通过大量迭代完成.因此,为验证温度比拟法在数值求解中的精度,在相同的计算假设、流体力学参数以及边界条件下,采用深埋隧道的退化轴对称解与圆形隧道的温度比拟法对隧道在开挖未支护、施作衬砌以及围岩注浆3种工况下的计算结果进行对比.轴对称解[4,13-14]的计算示意如图1所示,计算方法见式(1).
考虑到实际工程的边界条件与理论轴对称解有所不同[4],选取基于FLAC3D的流固耦合法模拟实际渗流场,并重新建立与之对应的ANSYS分析模型,再次将3种工况下的计算结果进行对比.

图1 深埋隧道退化轴对称模型示意Fig.1 Axis-symmetric model of the deep buried tunnel

(1)
式中:F为衬砌外水压力;γ为水的重度;H为地下水水头;kl为衬砌渗透系数;kg为注浆圈渗透系数;km为围岩渗透系数;r0为衬砌内径;rg为注浆圈外径;rl为衬砌外径;kl、kg和km均可替换为相应的导热系数.
2.1 温度比拟法与轴对称解比较
2.1.1计算模型
数值计算采用SOLID70单元模拟围岩、衬砌和注浆圈,计算模型如图2所示,衬砌内半径r0=5.0 m,外半径rl=5.3 m,厚度0.3 m,注浆圈厚度h=5 m.地下水位恒定,衬砌内侧为自由水面,水头高度为0.

图2 数值计算模型Fig.2 Tunnel geometry used in the numerical simulations
2.1.2开挖未支护时计算结果比较
隧道开挖未支护时,分别计算km=2×10-4~2×10-7cm/s,H=20~100 m时,rl=5.3 m处(即施作衬砌后衬砌外侧对应位置)的围岩水压.以H=20 m为例,围岩水压分布如图3所示.经计算,地下水水头恒定时,围岩水压的分布不随围岩渗透系数改变,因此,仅给出不同地下水水头时,rl=5.3 m 处衬砌对应位置围岩的水头值,如表1所示.
由图3及表1可得如下结论:
(1) 由两种方法得到的渗流场分布规律基本相同,即衬砌对应位置的水头值不随围岩渗透系数改变,仅随地下水水头高度的增长出现缓慢增长.隧道开挖未支护时,只要地下水排导通畅,渗流达到稳态后,衬砌对应位置的水头值较小.
(2) 温度比拟法可由云图直观得出水压的均匀层状分布规律,并能反应地下水由外向内的渗流方向.
(3) 温度比拟法和轴对称解的计算结果在地下水水头较低(H=20 m)时相等,增大水头高度后,两种方法的误差增大,但最大误差(H=100 m)仅为0.333%.
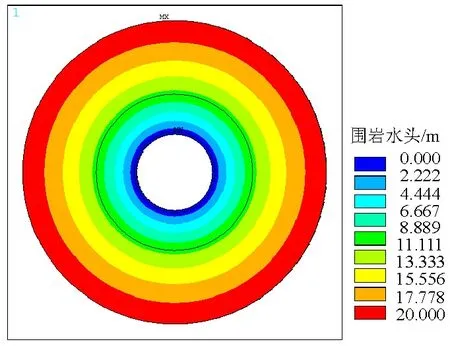
图3 H=20 m工况下开挖未施作衬砌时水压分布Fig.3 Distribution of water pressure after excavation under H=20 m
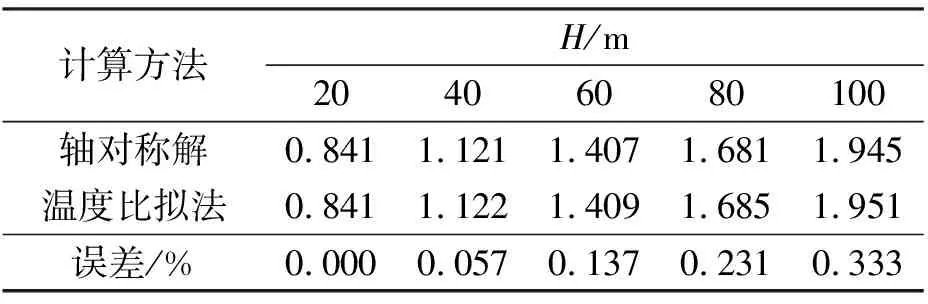
表1 开挖未支护时衬砌外侧水头值Tab.1 Water pressure of the lining after excavation under different operation conditions m
2.1.3施作衬砌后计算结果比较
隧道施作衬砌后能有效阻止地下水的排放、承担外水压力,但由于衬砌背后防排水系统的存在,也需考虑衬砌结构具有一定的透水性.本次计算取kl=1×10-6~1×10-8cm/s,km=2×10-4cm/s,各工况下衬砌外侧的水头值见表2.H=20 m,kl=1×10-6cm/s时,衬砌外水压力分布如图4.
由图4及表2可得如下结论:
(1) 两种方法得到的计算结果基本相同,由图4可知,施作衬砌会影响围岩水压的整体分布,由隧道开挖未支护时的均匀层状分布变为两段式分布,水压从衬砌内侧到衬砌外侧显著增长.与隧道开挖未支护时相比,施作衬砌后,衬砌外水压力明显增大.
(2) 施作衬砌后,衬砌渗透系数相同时,衬砌外水压力随地下水水头的增大而增大;地下水水头相同时,衬砌外水压力随衬砌渗透系数的减小而增大.
(3) 温度比拟法和轴对称解的计算结果误差随地下水水头的增大而增大,但最大误差(H=100 m)仅为0.275%.
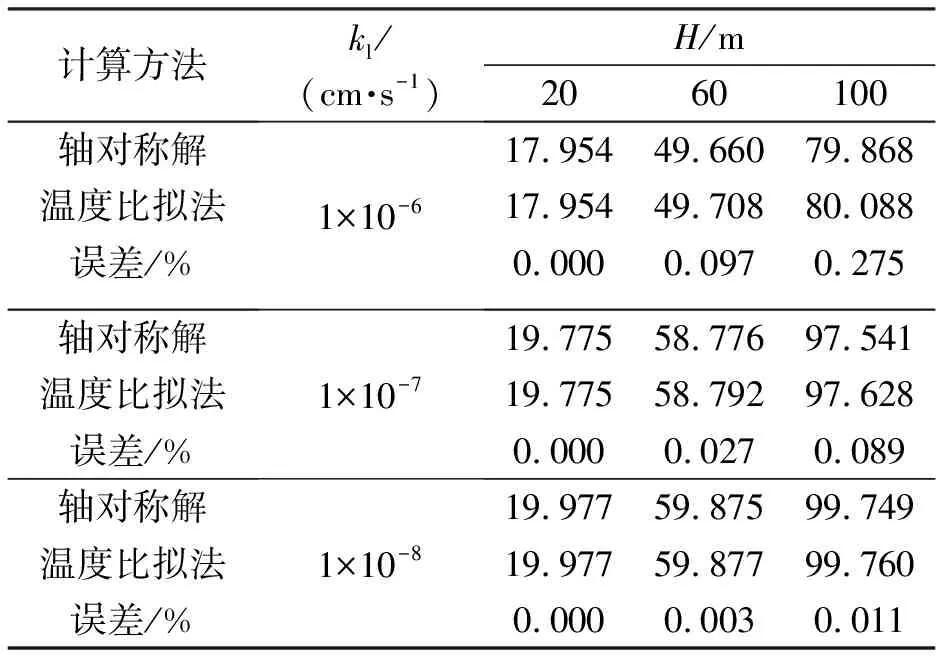
表2 施作衬砌后衬砌外侧水头值Tab.2 Water pressure of the lining after lining construction under different operation conditions m

(a) 整体模型
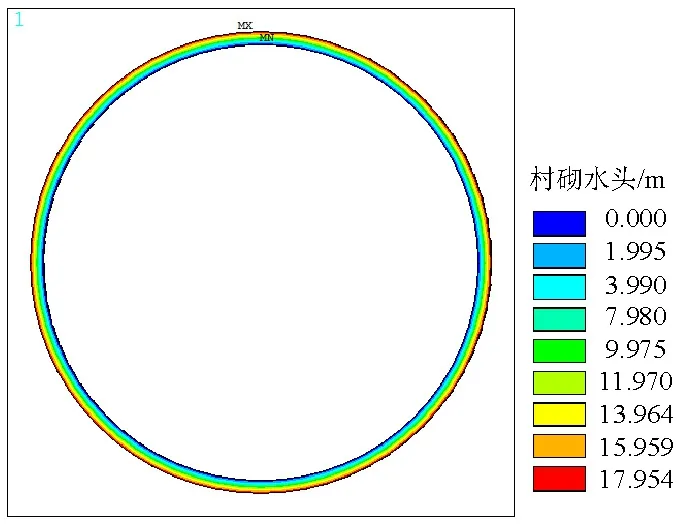
(b) 衬砌图4 H=20 m工况下施作衬砌后水压分布Fig.4 Distribution of water pressure after lining under H=20 m
2.1.4围岩注浆后计算结果比较
在“堵水限排”体系中,注浆圈能够改变围岩的渗透性能,增加地下水在渗流过程中消耗的能量,起到加固围岩、堵水消能的作用[15-16].当km=2×10-4cm/s,kl=1×10-6cm/s,h=5 m时,各工况下衬砌外侧的水头值见表3.H=20 m,kg=4×10-6cm/s时,模型整体、注浆圈以及衬砌水压分布如图5所示.由图5及表3可得如下结论:
(1) 与以上工况相同,两种方法的计算结果较为吻合,注浆圈能够和衬砌结构共同承载地下水压力,与仅施作衬砌相比,围岩注浆后,衬砌外水压力减小.并且,温度比拟法还能清楚显示在围岩和衬砌之间形成了一个水压的过渡缓冲区.
(2) 围岩注浆后,注浆圈渗透系数相同时,衬砌外水压力随地下水水头的增大而增大;地下水水头相同时,衬砌外水压力随注浆圈渗透系数的减小而减小.
(3) 温度比拟法和轴对称解的计算结果误差随地下水水头的增大而增大,但最大误差(H=100 m)仅为0.062%.
针对不同的断面形式,文献[6,17-18]中利用等效周长法实现了马蹄形、方形等断面和圆形断面之间的转化,拓展了轴对称解的适用范围.但对于更为复杂的断面形式,如连拱隧道,温度比拟法能不受断面形式的限制,依照实际工程建立模型.ANSYS的二次开发语言还可高效实现工程参数的调整,为后续设计提供便利.
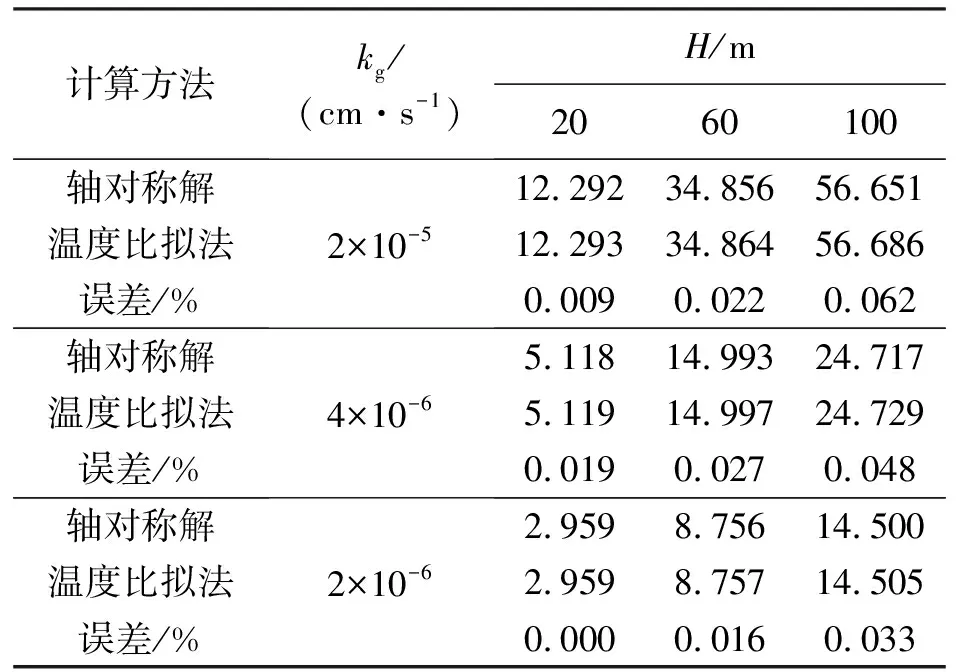
表3 围岩注浆后衬砌外侧水头值Tab.3 Water pressure of the lining after grouting under different operation conditions m
2.2 温度比拟法与流固耦合法比较
2.2.1计算模型
自隧道轴线起向两侧及上下边界各取100 m宽度,模型上边界和衬砌内侧为自由水面,地下水位恒定,隧道水平轴线处H=100 m.r0=5.0 m,rl=5.3 m,h=5 m,km=2×10-4cm/s,kl=1×10-6cm/s,kg=4×10-6cm/s.各结构选取SOLID70单元进行模拟,围岩参数取值见表4.
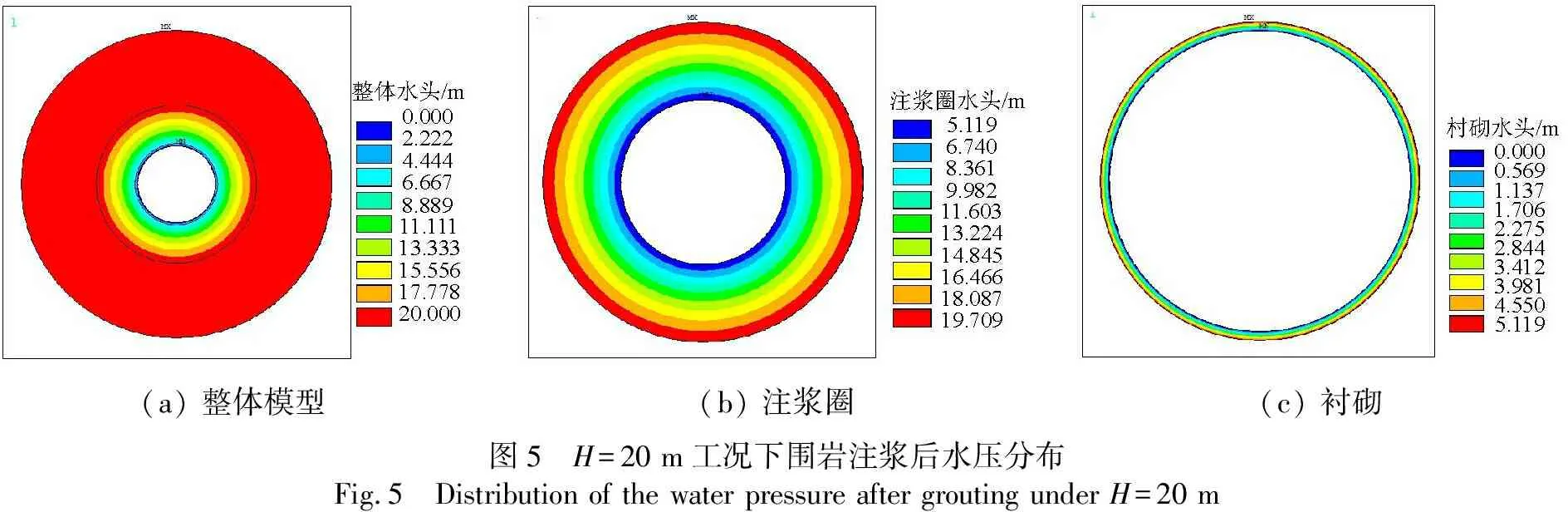
(a) 整体模型(b) 注浆圈(c) 衬砌图5 H=20 m工况下围岩注浆后水压分布Fig.5 Distribution of the water pressure after grouting under H=20 m

表4 围岩参数Tab.4 Parameters of the rock
2.2.2计算结果比较
计算仍考察隧道在开挖未支护、施作衬砌以及围岩注浆3种工况下衬砌外侧(rl=5.3 m处)的水头值,计算结果及其误差如表5所示.
由表5可得,温度比拟法与流固耦合法的计算结果误差在拱顶处最大,为14.8%,在边墙处最小,为1.5%.在既定的计算假设下,能够满足工程需要,且计算用时较短.

表5 各工况下衬砌外侧水头值比较Tab.5 Comparison of the water pressure of the lining under different operation conditions m
3 三维精细化计算实例
3.1 计算模型及参数
选取高速公路隧道典型双车道马蹄形断面,建立围岩-注浆圈-防排水系统三维精细化模型,分别计算注浆前、后衬砌水压在隧道横、纵断面上的分布规律,各计算参数为:隧道净宽11 m,净高8.68 m,衬砌厚度0.5 m,注浆圈厚度5 m.计算模型由隧道中心点向两侧及上下表面各取约5倍洞径宽度,为50 m(图6(a)).纵向建立3环环向排水管,相邻两环构成一个排水区间,间距10 m,地下水通过环向、纵向排水盲管以及中央排水沟进行排导(图6(b)),该模型较为详细地反应了当前公路隧道防排水系统的真实情况.以上各结构选取SOLID70单元进行模拟(图6(c)),围岩参数沿用表4取值,由于实际工程计算无法将围岩直接视为均质体,因此,围岩及结构物使用等效渗流系数通过工程类比和经验取值确定[19-22],如表6所示.
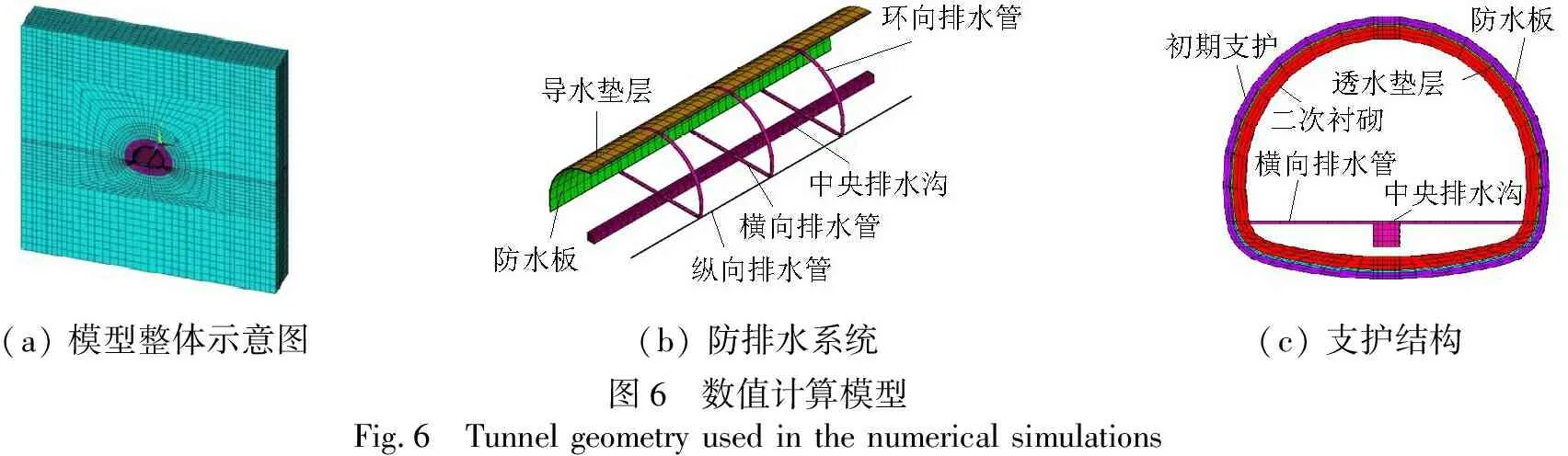
(a) 模型整体示意图(b) 防排水系统(c) 支护结构图6 数值计算模型Fig.6 Tunnel geometry used in the numerical simulations
3.2 计算结果分析
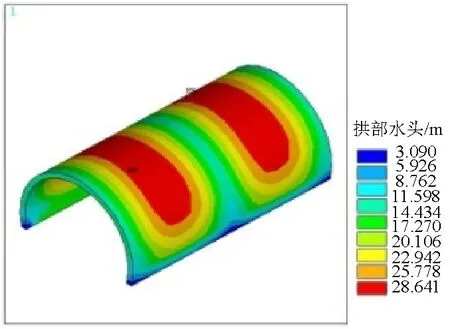
由于注浆前、后衬砌水压分布的规律相似,仅代表性地选取地下水水头H=60 m时,衬砌中部两排水节间在注浆之前的水压分布规律,如图7所示.注浆前、后衬砌各关键部位在横断面和纵断面上的水压值见图8.

表6 围岩及结构物等效渗透系数Tab.6 Permeability coefficient of the rock and structure cm/s
(a) 拱部

(b) 仰拱图7 二次衬砌水压分布Fig.7 Distribution of water pressure of the second lining
由图7、8可得如下结论:
(1) 注浆前、后衬砌外水压力的纵向分布规律均受环向排水管位置的影响.纵向排水管以上的部位,衬砌水压呈现周期性分布,每个排水区间形成一个分布周期,周期长度为相邻两环向排水管的间距(本次计算为10 m);而纵向排水管下方的仰拱,由于并没有设置环向排水管,衬砌水压沿纵向基本保持不变.
(2) 纵向排水管以上即拱部水压在每个周期上的分布规律为:在排水节间中部水压最大,在环向排水管处水压最小.
(3) 衬砌水压在横断面的分布规律受纵向排水管位置的影响.由于纵向排水管设在拱脚处,因此,横断面水压呈现倒葫芦形,在拱脚处最小,在拱顶和仰拱处较大.
(4) 围岩注浆后,衬砌外水压力明显减小,但折减幅度存在差异.其中,拱顶水压折减幅度最大,约为55%;仰拱水压折减幅度最小,约为45%.可见,注浆圈能够起到“堵水消能”的作用,有效降低二衬背后的水压,提高结构的安全性能.

(a) 注浆前纵断面水头值

(b) 注浆后纵断面水头值
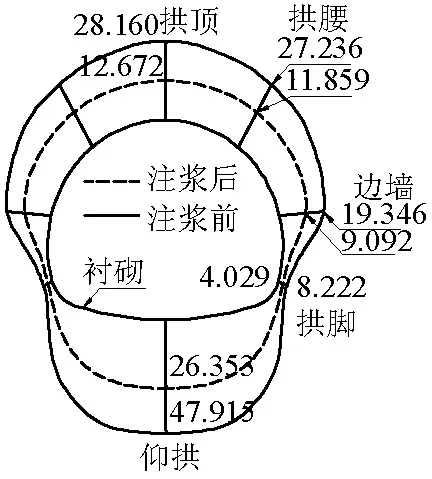
(c) 注浆前、后横断面水头值(单位:m)图8 二次衬砌水压变化规律Fig.8 Change rule of water pressure of the second lining
另外,虽然排水管处水压较小,但其作为地下水的排导通道,一旦堵塞,将导致横断面其它部位的水压急剧增大;同时,隧道拱部由于直接受到围岩来水的作用,如若出现排水不畅或施工质量等问题,必然导致衬砌结构承受较大的偏压水头,造成衬砌在运营期出现渗漏水.因此,保障排水系统的施工质量以及运营期间的疏通维护至关重要.针对排水节间中部水压较大的问题,建议通过围岩注浆、加密环向排水管、加大排水管直径以及预留排水管引排衬砌背后的地下水等措施削弱排水节间中部的水压峰值,改善衬砌的受力性能,确保隧道结构的安全.
3.3 与FLAC3D计算结果比较
为验证温度比拟法在三维精细化模型中的准确可靠性,采用基于FLAC3D的流固耦合法计算相同边界条件下衬砌水压的分布规律,计算结果对比见表7.由表7可知,三维计算时,温度比拟法快速、高效的优势更为明显,两种方法计算的衬砌水压最大误差出现在仰拱处,为14.5%.
可见,温度比拟法可良好地解决较为复杂的实际工程问题.该法作为单一渗流场的分析方法,虽不能考虑流固耦合效应以及时间对渗流场的影响,但能不受模型单元尺寸的限制大量节省计算时间、大幅提高计算效率,直观反应渗流场的分布规律,并且计算误差能够满足工程需要,不失为一种快速、准确、便捷求解衬砌外水压力的方法.

表7 衬砌外侧各部位的水头值Tab.7 Water pressure of the lining in different parts m
4 结 论
针对山岭隧道“堵水限排”体系,通过研究隧道开挖未支护、施作衬砌以及围岩注浆3种工况下衬砌外水压力的变化规律,将温度比拟法的计算结果与理论解析法轴对称解以及流固耦合法进行对比,验证了温度比拟法在单一渗流场计算中的精度,进而针对高速公路隧道典型双车道马蹄形断面建立围岩-注浆圈-防排水系统三维精细化模型,研究注浆前、后衬砌外水压力在隧道横断面和纵断面上的分布规律,得到如下有益结论:
(1) 温度比拟法与轴对称解计算的衬砌水压相比,结果误差随地下水水头的增大而增大,最大误差仅为0.333%;与流固耦合法相比,最大误差为14.8%.在既定的计算假设下,满足工程精度,不受模型单元尺寸的限制且节省了大量的计算时间,为求解衬砌外水压力提供了一种高效、准确、便捷的方法.
(2) 针对圆形深埋隧道,开挖未支护时,围岩水压呈现均匀层状分布,施作衬砌后变为两段式分布,衬砌外水压力明显增大,围岩注浆后,注浆圈在围岩和衬砌之间可形成一个水压过渡缓冲区,使衬砌外水压力减小.
(3) 针对双车道高速公路马蹄形断面隧道的围岩-注浆圈-防排水系统,衬砌外水压力的纵向分布规律受环向排水管间距的影响,在纵向排水管以上呈周期性分布,周期长度为相邻两环向排水管的间距,水压在排水节间中部最大,在环向排水管处最小;纵向排水管以下则基本保持不变.衬砌外水压力的横向分布规律受纵向排水管位置的影响,呈现倒葫芦形,在拱脚处最小,在拱顶和仰拱处较大.
[1] 王建宇. 对隧道衬砌水压力荷载的讨论[J]. 现代隧道技术,2006,43(增刊1): 67-73.
WANG Jianyu. Discussion of the tunnel lining water pressure load[J]. Modem Tunnelling Technology, 2006, 43(Sup.1): 67-73.
[2] 任旭华,陈祥荣,单治钢. 富水区深埋长隧洞工程中的主要水问题及对策[J]. 岩石力学与工程学报,2004,23(11): 1924-1929.
REN Xuhua, CHEN Xiangrong, SHAN Zhigang. Water problems and corresponding countering measures in projects of deep-lying long tunnels location in water-rich regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(11): 1924-1929.
[3] 中华人民共和国水利部. SL279—2002水工隧洞设计规范[S]. 北京:中国水利水电出版社,2002.
[4] 王建宇. 隧道围岩渗流和衬砌水压力荷载[J]. 铁道建筑技术,2008(2): 1-6.
WANG Jianyu. Problems on external water pressure on tunnel lining[J]. Railway Construction Technology, 2008(2): 1-6.
[5] 王建秀,杨立中,何静. 深埋隧道外水压力计算的解析-数值法[J]. 水文地质工程地质,2002,29(3): 17-19.
WANG Jianxiu, YANG Lizhong, HE Jing. The simulation of deep tunnel external water pressure by analytical-numerical method[J]. Hydrogeology and Engineering Geology, 2002, 29(3): 17-19.
[6] 郑波. 隧道衬砌水压力荷载的实用化计算研究[D]. 成都:中国铁道科学研究院,2010.
[7] 王建宇. 再谈隧道衬砌水压力[J]. 现代隧道技术,2003,40(3): 5-10.
WANG Jianyu. Once more on hydraulic pressure upon lining[J]. Modern Tunnelling Technology, 2003, 40(3): 5-10.
[8] 许玉景,孙克俐,黄福才. ANSYS软件在土坝渗流稳定计算中的应用[J]. 水力发电,2003,29(4): 69-71.
XU Yujing, SUN Keli, HUANG Fucai. Application of ANSYS in the earth dam seepage flow stability computation[J]. Journal of Hydroelectric Engineering, 2003, 29(4): 69-71.
[9] 李耀柱,林钢. 基于ANSYS温度场模拟的均质土坝稳定渗流数值计算[J]. 水运工程,2009(2): 48-51.
LI Yaozhu, LIN Gang. Computation of stable seepage flow of homogeneous earth dam based on the ANSYS function of temperature field method[J]. Protection and Waterway Engineering, 2009(2): 48-51.
[10] 贺晓明,李智录,王淑贤. 利用ANSYS热分析模块分析渗流场问题的探究[J]. 工程地质计算机应用,2005(4): 26-29.
[11] 张政. 岩溶地区公路隧道渗漏水处治原则研究[D]. 成都:西南交通大学,2014.
[12] 蒋进. 高压富水地层山岭隧道衬砌受力机制探讨与结构设计[D]. 重庆:重庆交通大学,2012.
[13] 郑波,王建宇. 圆形隧道围岩与衬砌渗透力解析解[J]. 武汉理工大学学报:交通科学与工程版,2011,35(1): 19-23.
ZHENG Bo, WANG Jianyu. Analytical solutions for seepage forces of circular tunnel surrounding ground and lining[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2011, 35(1): 19-23.
[14] 王秀英,王梦恕,张弥. 山岭隧道堵水限排衬砌外水压力研究[J]. 岩土工程学报,2005,27(1): 125-127.
WANG Xiuying, WANG Mengshu, ZHANG Mi. Research on regulating water pressure acting on mountain tunnels by blocking ground water and limiting discharge[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 125-127.
[15] 王秀英,王梦恕,张弥. 计算隧道排水量及衬砌外水压力的一种简化方法[J]. 北方交通大学学报,2004,28(1): 8-10.
WANG Xiuying, WANG Mengshu, ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J]. Journal of Northern Jiaotong University, 2004, 28(1): 8-10.
[16] 庄宁,朱合华,杨向东,等. 高水压下隧洞合理断面形状研究[J]. 地下空间与工程学报,2005,1(5): 713-716.
ZHUANG Ning, ZHU Hehua, YANG Xiangdong, et al. Research on proper cross section shape of high water pressure tunnel[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(5): 713-716.
[17] 王志杰,何晟亚,袁晔,等. 基于等效周长法研究隧道衬砌水压力荷载及内力[J]. 铁道科学与工程学报,2015,12(3): 577-583.
WANG Zhijie, HE Shengya, YUAN Ye, et al. Study on water pressure load and internal force of tunnel lining based on the method of equivalent perimeter alternative[J]. Journal of Railway Science and Engineering, 2015, 12(3): 577-583.
[18] 何明磊,胡磊,孟祥磊. 隧道衬砌水压力荷载及内力研究[J]. 铁道标准设计,2014,58(2): 79-83.
HE Minglei, HU Lei, MENG Xianglei. Research on water pressure load and internal force of tunnel lining[J]. Railway Standard Design, 2014, 58(2): 79-83.
[19] 邱月,何聪,邹育麟,等. 富水隧道基于温度比拟法的合理注浆参数研究[J]. 铁道科学与工程学报,2016,13(4): 723-729.
QIU Yue, HE Cong, ZOU Yulin, et al. Study on the appropriate parameters of grouting circle for tunnel base on temperature analogy method in water-enriched region[J]. Journal of Railway Science and Engineering, 2016, 13(4): 723-729.
[20] 中华人民共和国水利部. GB50487—2008水利水电工程地质勘查规范[S]. 北京:中国水利水电出版社,2009.
[21] 邹育麟. 高速公路营运隧道渗漏水防治与维护综合技术研究[D]. 成都:西南交通大学,2015.
[22] 何聪. 高压富水地区隧道渗流场分析与衬砌抗水压力对策研究[D]. 成都:西南交通大学,2015.
