颤振临界风速计算值与试验值的一致性
2018-06-01李志国廖海黎
伍 波, 王 骑, 李志国, 廖海黎
(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 西南交通大学风工程四川省重点实验室, 四川 成都 610031)
随着桥梁建造技术的进步和桥梁跨度的显著增加,桥梁的颤振显得越来越重要,而如何准确计算桥梁的颤振临界风速又是大跨度桥梁乃至超大跨度桥梁设计时最需要解决的问题.至今为止,国内外已经对桥梁颤振计算方法做了相当多的研究,也取得了丰硕成果.现在比较常用的颤振分析方法,主要包括:复特征值法(complex eigenvalue analysis, CEV)[1]、Masumoto提出的分步分析方法[2]、时域分析方法[3]、双模态耦合闭合解法[4].这些方法涉及的自激气动力,皆源于Scanlan等[5]在1971年提出的以颤振导数表示的气动力模型,由此派生出来的颤振导数识别方法[6-8]也在理论上具有相当高的精度.
尽管颤振导数的识别方法和颤振分析方法的准确性已在薄平板算例及机翼算例中得到了很好的验证,理论本身的正确性是毋庸置疑的.但对于桥梁颤振计算来说,即使在小振幅情况下,理论计算结果与风洞试验测试值之间总会存在或多或少的差异,尤其在断面较钝或攻角较大的情况下,这种差异更加明显.Argentini等[9]针对某大跨度悬索桥进行全桥气弹模型试验及多模态复特征值颤振分析,结果显示即使在考虑了全模态(full-set)的情况下,颤振临界风速计算结果与试验结果仍有一定差别.丁泉顺[10]对不同攻角下江阴大桥的颤振分析结果显示,小攻角下,颤振风速理论计算结果与试验结果保持一致,而在3°攻角下,计算值与试验值的差异明显增大.Ge等[11]针对H型断面及箱形断面进行二维颤振分析,结果显示H型断面的计算误差明显大于箱形断面.这样的差异性曾被认为是气动力的高次谐波效应引起.但王骑等[12-13]在扁平箱梁和矩形断面的强迫振动风洞试验研究中发现,在小振幅条件下,两种断面均没有观察到显著的高次谐波分量,即便是在中等振幅条件下(扭转角达到10°),其自激气动力中的高次谐波分量比重仍然不大,由此可知,造成此差异性的原因还另有他解.
为了详细研究桥梁颤振临界风速计算值和试验值之间的差异性,并发现其中可能的原因,本文以扁平箱梁为研究对象.首先利用强迫振动风洞试验获得断面颤振导数,并基于不同的动力参数组合计算获得了不同工况下颤振风速.其次采用常规的弹簧悬挂节段模型风洞试验技术,选取与计算相同的动力参数组合,测试并获得同一模型在不同风攻角下的不同颤振特性,包括临界风速、振幅比和相位角,并与计算结果进行对比.结果表明,0°风攻角下计算值和试验值一致性较好,而3°和5°风攻角下计算值和试验值有较大的差异性.最后基于计算的和试验的颤振因子对比以及颤振因子与颤振相位角成正变的特性,推断出在攻角较大时,耦合相位角可能会对颤振导数产生不可忽略的影响,从而导致颤振风速计算值和试验值产生差异.
1 风洞试验参数与计算方法
1.1 强迫振动试验及颤振导数识别
本文以某扁平箱梁断面为对象,制作了缩尺比为 1∶80 的节段模型,模型长度为1.1 m,宽度为0.4 m,梁高为0.041 m,高宽比为9.7.模型断面如图1所示,强迫振动风洞试验如图2 所示.

图1 试验模型断面Fig.1 Cross-Section of model

图2 强迫振动风洞试验Fig.2 Forced vibration testing for section model
利用强迫振动试验装置,通过记录模型在不同风速及不同风攻角下的竖向及扭转单自由度运动的气动自激力和位移,识别模型在不同工况下的颤振导数.试验中采取的振动频率为2.5 Hz,竖向试验振幅为10 mm,扭转试验振幅为2°.竖向和扭转运动引起桥梁断面自激气动力分别为
(1)
(2)

试验时的折算风速V=U/(fb),其中,f为强迫振动频率,Hz,折算风速范围从4~20.
1.2 颤振计算方法
本文选择双模态耦合闭合解法[4]进行颤振临界风速计算.该方法不仅能够简便和精确地计算桥梁的颤振临界风速,也可求解出模态频率、阻尼及相位等参数随着折减风速的变化.同时,由于该方法将颤振风速表示为动力部分和气动部分的乘积,使得研究中可以单独量化这两部分的影响,有利于分析导致颤振风速计算值和试验值出现差异的原因.该计算方法具体表达式为
(3)
(4)
(5)
(6)
式中:Uc为是颤振临界风速;ωs1和ωs2分别为竖向运动和扭转运动的圆频率;m为主梁单位长度等效质量;r为等效质量的惯性半径;γ为表征颤振导数影响的系数,本文称为颤振因子,反应了气动力变化对颤振的影响;ξs2为扭转运动的结构阻尼比,%;υ=ρb4/I,I为单位长度等效质量惯性矩;D为表征弯扭振型相似度的因子,对于节段模型试验D=1.
根据耦合颤振闭合解简化计算方法[4],最终的颤振风速则是式(3)的风速值曲线和式(7)的风速值曲线的交点.
(7)

此外,还可以通过风洞试验获得的颤振风速和试验系统动力参数反算出颤振因子,本文称为试验颤振因子,如式(8).
(8)
式中:Ucs为颤振临界风速试验值.
利用上述颤振计算方法及测量得到的颤振导数,即可计算不同动力参数组合下的颤振临界风速,主要的计算工况如表1所示.利用强迫振动试验装置得到的决定颤振临界风速的4个关键颤振导数如图3所示.

表1 颤振性能计算及测试工况Tab.1 Calculating and testing cases for flutter
注:fh、ft分别为系统竖向频率及扭转频率,Hz;M、Im分别为系统总质量及质量惯性矩,kg、kg·m2;
ξs1为系统竖向阻尼比,%;η为系统的弯扭频率比.
1.3 自由振动试验模型及工况
制作了缩尺比为 1∶50 的节段模型进行弹簧悬挂节段模型风洞试验.试验在XNJD-1第二试验段的均匀流场中进行(试验段截面尺寸为2.4 m×2.0 m,最大试验风速为45 m/s),采用可模拟二自由度耦合运动(竖向运动及扭转运动)的弹簧悬挂系统进行不同风攻角下的节段模型颤振性能测试.

(a) H3(b) A∗1(c) A∗2(d) A∗3图3 试验断面不同攻角下4个关键颤振导数的测试结果Fig.3 Flutter derivatives of the girder under different angle of attacks
为了较详细地反映颤振风速计算值和试验之间的差异,试验中通过改变配重的质量及质量惯性矩来改变试验系统的Scruton数[14]并满足与计算工况相同的动力参数组合.
2 计算结果和试验结果的对比

从表2中可以看出:对于0°攻角,颤振临界风速试验值与计算值之间具有良好的吻合度;对于工况1~6,不同动力参数下颤振折算风速最大计算误差为4.9%,其试验值为8.35,计算值为7.96,对应的为工况3,最小计算误差为0.12%,计算值为8.63,试验值为8.62,对应的为工况1;0°攻角下的计算结果表明,利用颤振导数计算的颤振临界风速和颤振频率,无论在何种动力参数条件下,均能够和风洞试验值高度吻合.
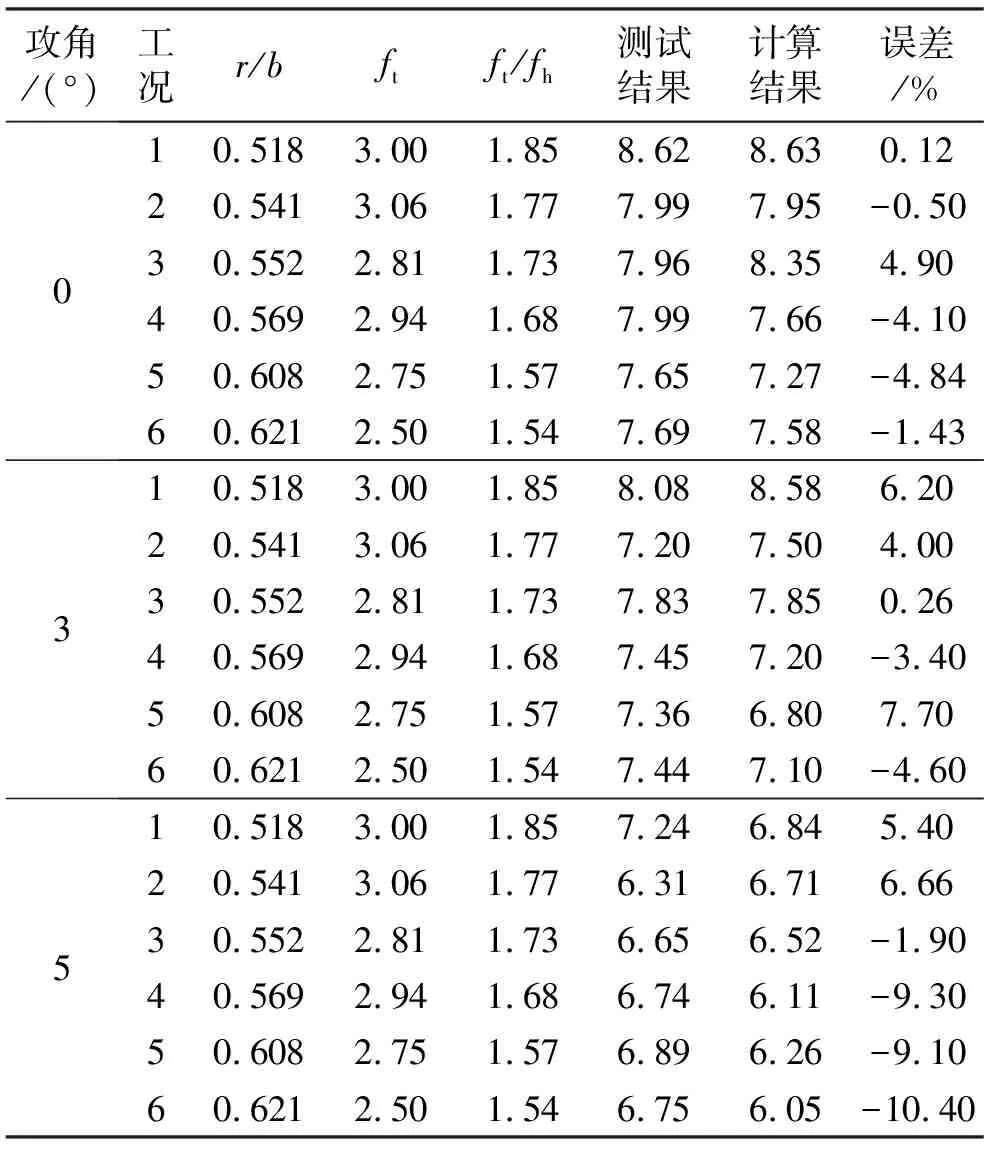
表2 颤振临界风速试验值与计算值的对比Tab.2 Comparison of calculated results and tested results of critical flutter speed
随着攻角增大,计算结果与实验结果的吻合度逐渐降低.从图3可以看出:在3°攻角,工况5下颤振折算风速计算值和试验值分别为6.80和7.37,最大差异达到7.7%;工况1下对应的计算和试验差异为6.2%;在5°攻角下,两者间的差异进一步增大;工况6下的计算折减风速为6.05,试验折减风速为6.75,误差达到了10.4%,对于5°攻角下的其他测试工况,计算值和试验值的差异性也很明显,如工况4的差异为9.3%,工况5的差异为9.1%,工况2的差异为6.66%,工况1的差异为5.4%.
由此可以得出,在有攻角的情况下,除了颤振临界风速本身较攻角0°下的值有显著降低外,临界风速的计算结果与试验结果间的差异也显著增加,尤其在5°攻角下,该差异达到最大.需要说明的是,在有风攻角的条件下,这样的差异在其他桥梁断面的风洞试验数据中可以找到[9-11].
3 颤振风速差异的原因分析
3.1 差异离散性的量化
由于在不同风攻角下相同试验工况的动力参数是相同的,因此可以推知颤振临界风速的差异性不是由动力参数的改变引起的,而是由气动力的变化引起的.基于此,采用式(3),可以将动力参数的影响与气动参数的影响分离开.根据现有颤振理论,颤振导数只与断面的气动外形有关,因此只要在相同风攻角下,无论结构的动力参数如何改变,颤振导数均保持不变,那么颤振因子的值会保持稳定,同时试验颤振因子和理论颤振因子的值应保持一致.基于此推论,通过分析颤振因子的值是否保持一致以及其理论值和试验之间的差异,就可推测出引起颤振临界风速差异的原因.
采用实测的颤振导数,结合式(4)可以获得理论上的γ,由此可量化气动力对颤振的影响;利用每个工况所对应的系统动力参数,结合节段模型试验所获得的颤振临界风速,采用式(8)可反算出各个工况对应的试验颤振因子γs.为了分析颤振因子数值的稳定性,再定义参数C1和C2用以表征颤振因子在不同工况下的相对变化,其表达式如下所示:
(9)
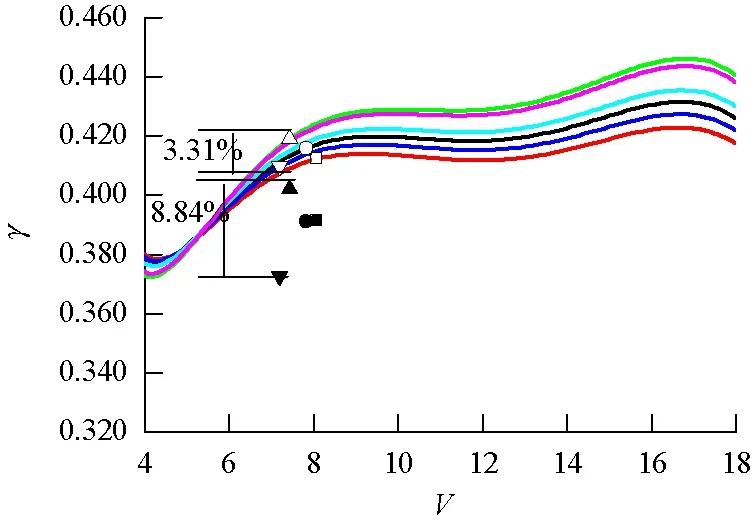
计算和试验条件下的颤振因子和对应的C1和C2值如表3所示.从表3可以看出:对于颤振导数计算获得的理论颤振因子,无论在哪个攻角下,都比较集中和稳定,彼此间差异值C1基本都在2%以下;对于试验风速反算的颤振因子γs以及差异值C2,除了在攻角0°下颤振导数的值稳定外(C2<5%),在攻角3°和5°下,C2都超过了5%.如在0°攻角时,颤振因子分布在[0.407,0.426]之间,C2最大为4.5%;在攻角3°条件下,颤振因子分布在[0.372,0.409]之间,C2增大到8.8%,折算风速区间也缩短为[7,8];攻角5°时,颤振因子分布在[0.336,0.381],C2上升到了11.8%,对应的折算风速区间缩短为[6,7].图4则直观给出了颤振因子的计算值和测试值的相对变化.图4中所示理论曲线为利用式(4)和颤振导数计算得到的不同折算风速下的颤振因子曲线,空心点为相应工况的颤振临界状态对应的颤振因子计算值γs;图中实心点为相应工况在试验颤振临界风速处利用式(8)反算得到的颤振因子γs。
在攻角0°下,试验颤振因子与计算的颤振因子保持一致,各个颤振因子也均被包围在理论颤振因子随折算风速变化的曲线中.但在攻角3°和5°下,试验颤振因子明显偏离了理论曲线,在颤振折算风速区间内的离散性显著高于理论曲线的离散性.

表3 颤振因子计算值与试验反算值对比Tab.3 Comparison of calculated results and tested results
由于系统的动力参数不会对颤振因子产生显著影响,由此还可以推知,在攻角3°和5°条件下,发生颤振时作用在模型上的实际气动力明显受到了某个因素的影响,导致颤振导数受到了影响.颤振过程中,能够影响颤振风速的有振幅、结构阻尼比和运动相位角3个因素.
3.2 振幅的影响
图5列举出了工况1对应的颤振临界状态下扭转运动和竖向运动的时程曲线.

(a) 风攻角0°
(b) 风攻角3°

(c) 风攻角5°

图4 颤振因子试验值与计算值对比Fig.4 Comparison of RC of flutter factors
从图5中可以看出,竖向运动和扭转运动的位移均很小,扭转振幅均在1°以内,竖向振幅在2 mm以内.其他未列举工况的振幅也在此范围内.根据Noda等[14]对于宽高比为13的矩形断面颤振导数的试验研究结论,在3°以内的扭转运动下和6.5 mm的竖向运动下,测试断面的颤振导数值保持不变.由此可以得出,试验中的颤振振幅不会影响颤振导数的取值.再讨论高次谐波的影响:根据王骑等[12]的强迫振动风洞试验结论,扁平箱梁在8°扭转振幅以内和20 mm竖向振幅以内,气动力中没有明显的高次谐波分量存在,由此排除了高次谐波分量对颤振的影响.

图5 颤振响应时程图Fig.5 Time-history response of flutter
3.3 结构阻尼比的影响

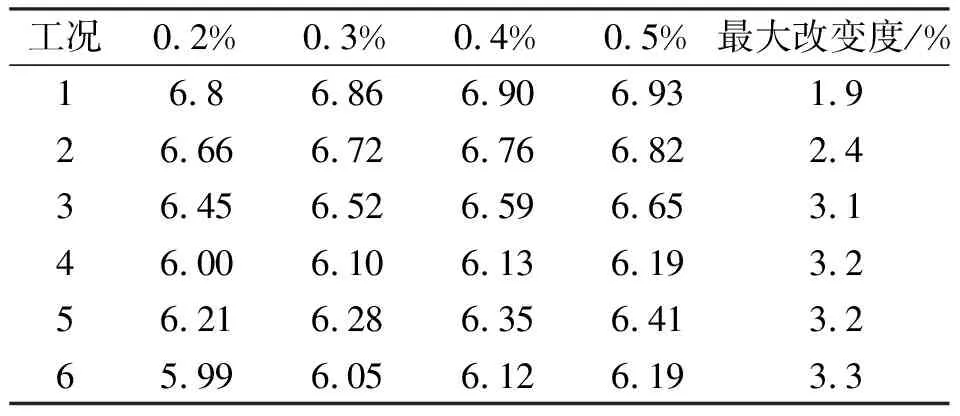
表4 不同结构阻尼比下颤振临界风速计算结果Tab.4 Critical velocities under different damping ratios m/s
结构阻尼比从0.2%变化到0.5%,颤振临界风速的最大相对变化仅为3.3%,对应的颤振因子最大变化值也为 3.3%.由此可知,结构阻尼比的显著变化不会引起颤振风速的显著变化,使其离散性显著增加,因此阻尼比不是扁平箱梁颤振临界风速试验值与计算值产生较大差异的原因.

表5 不同结构阻尼比下颤振因子计算结果Tab.5 Flutter factors under different damping ratios
3.4 相位角的影响
最后讨论颤振时相位角的影响.图6给出了在不同的攻角下,颤振因子及相位差随风攻角的变化曲线.从图6中可以看出:在攻角0°时,颤振因子几乎不随相位差的变化而变化,其所对应的相位差集中在区间[-0.55,-0.35],跨度为0.2;在攻角3°时,相位差集中在区间[-0.5,-0.25],跨度为0.25;在攻角5°时,相位差集中在区间[-0.45,0.03],跨度为0.5.因此可以得到这样的结论:随着攻角增大,发生颤振时的相位差变化区间增大,且在攻角3°和5°条件下,相位差越大,颤振因子的值越大,即颤振因子与相位差成正变关系.
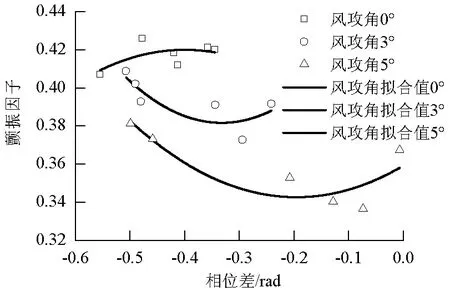
图6 颤振因子及相位差关系图Fig.6 Comparison of flutter factor and phase difference
基于以上分析可以得到:颤振时模型断面所受到的自激气动力受到了相位差影响而发生了变化,并由此引起了颤振导数的变化,即颤振时模型对应的实际颤振导数不同于单自由度振动下测试的颤振导数.事实上,早在1993年,颤振运动相位角对自激气动力的影响就被Matsumoto等[15]在风洞试验中发现和证实.2015年,Lee等[16]通过机翼的强迫振动试验证实了相位角对气动力的显著影响.2016年,Liao等[17]和Wang等[13]分别基于数值计算和强迫风洞试验,发现了同频耦合运动中的扁平箱梁和矩形断面的自激气动力是随着耦合相位角的变化而变化的,且不等于两个单自由度下气动力的叠加.
因此可以推测,在攻角3°和5°下,由于颤振时相位角的变化导致的颤振导数变化可能是计算颤振风速和试验颤振风速产生差异的原因.
4 结论和建议
通过对比扁平箱梁在不同攻角下颤振临界风速的理论计算分析与风洞试验验证,发现了大攻角下两者存在较大的差异,得到如下主要结论:
(1) 在攻角0°下,颤振临界风速计算值及试验值吻合,对于不同的测试工况,两者差异均在5%以内,但随着攻角增大,计算值与试验值间的误差也增大,在攻角5°下最大达到10.8%.
(2) 在攻角3°和5°下,通过对理论颤振因子和试验颤振因子差异的分析,可以推断出耦合颤振条件下,相位角的变化可能引起了颤振导数的变化,从而导致计算颤振风速和试验值产生差异.
基于本文所取得的各项研究数据和结论,提出如下建议:有必要进一步开展大攻角条件下弯扭耦合颤振相位差对扁平箱梁断面颤振导数带来的影响,以修正大攻角下的颤振临界风速.
[1] WILDE K, FUJINO Y, MASUKAWA J. Time domain modeling of bridge deck[J]. Structural Engineering Earthquake Engineering, 2010, 13(2): 93-104
[2] MASUMOTO M. Aerodynamic damping of prisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59(2/3): 159-175.
[3] CHEN X, MASUMOTO M, KAREEM A. Time domain flutter and buffeting response analysis of bridges[J]. Journal of Engineering Mechanics, 2000, 126(1): 7-16.
[4] CHEN X. Improved understanding of bimodal coupled bridge flutter based on closed-form solution[J]. Journal of Engineering Mechanics, 2007, 133(1): 22-31.
[5] SCANLAN R, TOMKO J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, 1971, 97: 1717-1737.
[6] SARKAR P P, JONES N P, SCANLAn R H. Identification of aeroelastic parameters of flexible bridges[J]. Journal of Engineering Mechanics, 1994, 120(8): 1718-1742.
[7] MATSUMOTO M, NIIHARA Y, KOBAYASHI Y, et al. Flutter mechanism and stabilization of bluff bodies[C]∥Proceedings of the Ninth ICWE. New Delhi: Wiley Eastern Limited, 1995: 827-838.
[8] CHEN X, KAREEM A. Efficacy of the implied approximation in the identification of flutter derivatives[J]. Journal of Engineering Mechanics, 2004, 130(12): 2070-2074.
[9] ARGENTINI T, DIANA G, ROCCHI D, et al. A case-study of double multi-modal bridge flutter: Experimental result and numerical analysis[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 151: 25-36.
[10] 丁泉顺. 大跨度桥梁耦合颤抖振响应的精细化分析[D]. 上海:同济大学,2001.
[11] GE Y J, XIANG H F. Computational models and methods for aerodynamic flutter of long-span bridges[J]. China Civil Engineering Journal, 2008, 96(10/11): 1912-1924.
[12] 王骑,廖海黎,李明水,等. 大振幅下薄翼和流线型箱梁的气动迟滞研究[J]. 实验流体力学,2013,27(1): 32-37.
WANG Qi, LIAO Haili, LI Mingshui, et al. Aerodynamic hysteresis of thin airfoil and streamline box girder under large amplitude oscillation[J]. Journal of Experiment in Fluid Mechanics, 2013, 27(1): 32-37.
[13] WANG Qi, LIAO Haili, LI Mingshui, et al. Coupling and nonlinearity and span-wise correlation in aerodynamic force of a rectangular cylinder[C]∥The 8th International Colloquium on Bluff Body Aerodynamics and Applications. Boston: [s.n.], 2016: 1-8.
[14] NODA M, UTSUNOMIYA H, NAGAO F, et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1): 101-11.
[15] MASUMOTO M, SHIRAISHI N, SHIRATO H, et al. Aerodynamic derivatives of coupled/hybrid flutter of fundamental structural sections[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1/2/3): 575-584.
[16] LEE T, SU Y Y. Surface pressures developed on an airfoil undergoing heaving and pitching motion[J]. Journal of Fluids Engineering, 2015, 137(5): 051105.
[17] LIAO H, WAN J W, WANG Q, et al. Numerical study on nonlinear and motion coupling effects on self-excited force of a bridge deck[C]∥The 8th International Colloquium on Bluff Body Aerodynamics and Applications. Boston: [s.n.], 2016: 1-8.
