湍流积分尺度对高层建筑风荷载影响的大涡模拟

祝志文, 邓燕华

(湖南大学土木工程学院, 湖南 长沙 410082)

结构抗风研究中,无论是风洞试验还是数值模拟,准确模拟大气边界层的湍流特性是保证研究结果可信的必要条件.早期的研究主要关心风速剖面和湍流强度剖面,以期得到与大气边界层相似的风速和湍流强度.卢占斌等[1]的风洞试验研究表明,湍流强度主要改变风压脉动值的大小和能量在各频谱范围的分布,湍流积分尺度的增大将使风压系数平均值的绝对值和均方根值均降低.JR等[2]研究矩形桥梁断面在风速和湍流强度不变的前提下,湍流积分尺度对风压系数平均值和均方根值、弯矩谱峰值的影响.Nakamura和Ozono[3]指出,当湍流积分尺度小于2D(D为结构特征长度)时,可以忽略其对湍流流态的影响;当大于2D时,湍流积分尺度增大,将对风压系数平均值产生显著影响.Li和Melbourne[4]研究湍流积分尺度在2.8D～7.8D范围内对结构风效应的影响,随湍流积分尺度的增加,小尺度湍流脉动运动量降低,压力系数峰值呈现增大趋势,当湍流积分尺度长度达到5D时出现降低现象.

风洞试验中要准确测定湍流积分尺度和保持湍流强度不变的前提下调整其值绝非易事.本文利用大涡模拟研究湍流积分尺度对高层建筑风荷载的影响.大涡模拟入口脉动风场生成的方法主要包括随机流生成技术(random fow generation， RFG)、离散和合成随机流生成法(discretizing and synthesizing random flow generation， DSRFG).文献[5]研究指出,RFG方法通过湍动能和耗散率求湍流积分尺度,DSRFG方法通过调整湍流积分尺度来调整流场特性,具有接近真实流的优点,但计算费用是RFG的fmax倍(fmax为采样频率的最大值),且普通计算机难于实现,只能在超算中心或超大集成机群上完成.本文通过调整湍流积分尺度,提高RFG计算精度,从而规避DSRFG方法中的不足.

1 数值模型

1.1 几何模型和测点布置

高层建筑模型采用CAARC (commonwealth advisory aeronautical research council)建筑,缩尺比为 1∶300,缩尺后的几何尺寸:长(Dy)152 mm×宽(Dx)102 mm×高(H)610 mm.竖向设8个测点层,各层高度见图1.

每个测点层设20个测点,测点总数160个.定义来流风速垂直于截面长边,测点1～5、6～10、11～15和16～20所在的面分别为迎风面、上侧面、背风面和下侧面,见图2.

1.2 计算域及网格划分

顺流向(x轴向)入口至模型中心的距离为7.5H,模型中心至出口的距离为15H,上下侧面距模型中心均为3.5H,模型顶部到上边界的距离为6H,计算得到的堵塞率为0.6%,显著小于风洞试验堵塞度上限值3%.

1.3 边界条件设定

边界条件设置为:入口设为速度,出口为自由流出口,地面和模型表面均为无滑移壁面,其他均为对称边界，模型壁面和地面的首层网格高度均为2×10-4Dx.

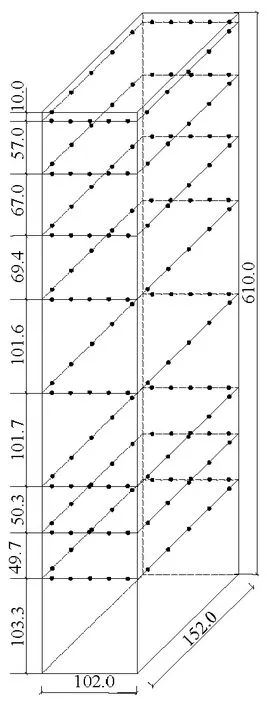
图1 测点层分布Fig.1 Arrangement of pressure layers

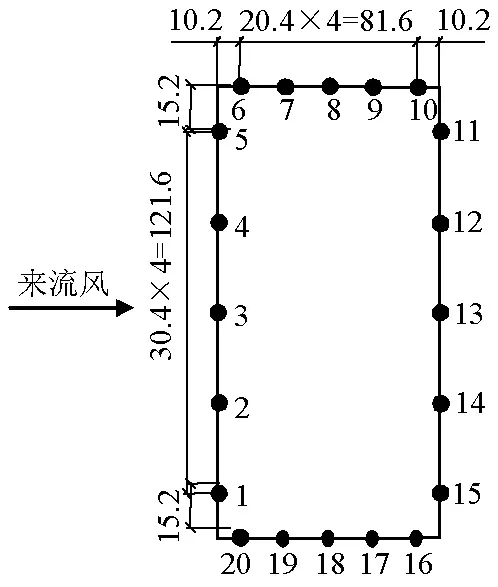
图2 测点平面布置Fig.2 Cross-section arrangement of pressure points

1.4 湍流模型

本文基于LES (large eddy simulation)湍流模型开展CFD (computational fluid dynamics)模拟,其控制方程为

(1)

(2)

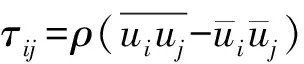
Cij=pij+Dij+Φij-Eij,

(3)

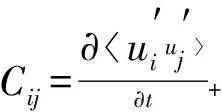
(4)

pij=-

(5)

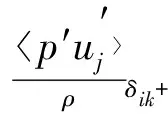
(6)

(7)

(8)

式中：Cij为雷诺应力在平均运动轨迹上的增长率;为湍动能的生成项;pij为雷诺应力通过平均运动的变形率向湍流脉动输入平均能量,当其大于0时，平均运动向脉动运动输入能量,湍动能增大，反之,湍动能减小；Dij为雷诺应力扩散项;Φij为再分配项,在湍流脉动各分量间起调节作用,实现能量的转移;Eij为湍动能耗散项；表示相应变量的系综平均值(即在给定的边界条件下一切可能运动状态的算术平均)；u下标的i、j和k为速度各方向的分量;u′下标的i、j和k为脉动速度各方向的分量;x下标的i、j和k为坐标轴x的i、j和k方向;p′为压强脉动值;ν是流体运动黏度;

采用Simple算法进行压力速度耦合,动量方程采用中心差分离散.每个时间步最大迭代20次,经时间无关性检查,确定时间步长b=0.000 5 s.

1.5 计算参数设置

为后续更好地与文献试验结果进行比较,入口风速和湍流强度均选用文献[7]的B类地貌风洞试验结果,风速为

U=12.98(z/1.167)0.16.

(9)

湍流强度为

I=0.085(z/1.167)-0.21.

(10)

湍流积分尺度Lu参照文献[8]并计入缩尺比后得到,即

Lu=1.054z0.5.

(11)

湍动能K和湍动能耗散率ε均参照文献[19],即

K=1.2(UI)2,

(12)

ε=0.090.75K1.5/(φLu),

(13)

式(9)～(13)中:

z为距地面高度；

φ为湍流积分尺度调整系数.

本文保持风速和湍流强度不变,将φ分别设置为0.4和1.0,得到相应的湍流积分尺度长度与钝体特征尺度长度之比k1=2.17和k2=5.42.将上述参数通过Fluent用户自定义函数(user defined function, UDF)导入Fluent软件.

2 数据处理

平均风压系数和脉动风压系数按文献[7]定义,其它气动参数按式(14)～(15)定义.

(14)

(15)

式(14)～(15)中:

Cd和Cl分别为平均阻力系数和升力系数;

CMx和CMy分别为顺风向和横风向基底弯矩系数平均值;

UH和Dy分别为模型顶部平均风速和模型迎风面宽度;

FD、FL分别为基底阻力和升力;

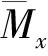
3 计算结果比较与分析

3.1 基底气动力的对比

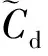
从表1可以看出,本文LES模拟结果与文献结果总体上趋于一致,模拟获得的气动力均方根值比风洞试验值小,但平均值与试验值吻合较好,模拟结果与文献[12]的数值模拟结果较接近.

表1 模拟结果与文献结果的比较Tab.1 Comparison of simulation results with other available

3.2 表面风压系数

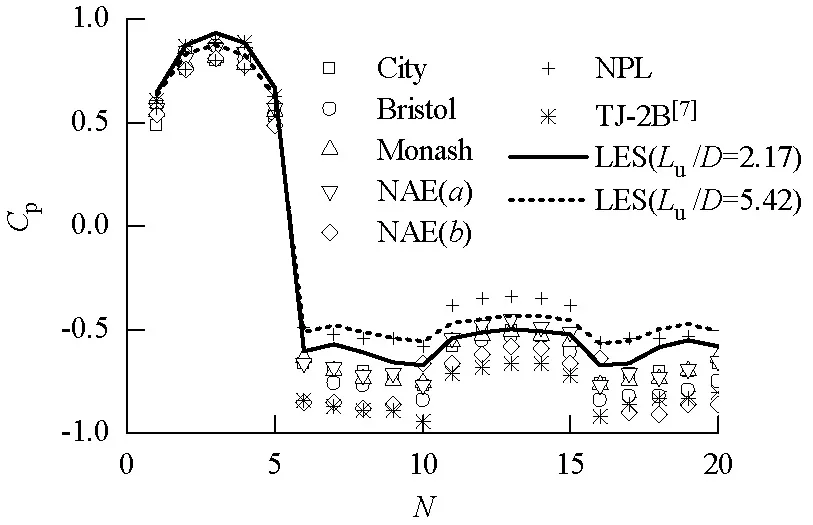
图3给出了2/3H高处的测点风压系数平均值Cp和均方根Cprms,图中,横坐标N为监测点编号,具体布置见图2.用机构名称中的关键词代表其机构名称,分别为:City代表City University, Bristol University of Bristol; Monash代表Monash University; NAE代表National Aeronautical Establishment(a、b分别表示该机构采用的两种大气边界层的模拟方法);NPL代表Nmional Physical Laboratory; TJ-2B代表同济大学TJ-2建筑风洞B类地貌风场.LES为本文的大涡模拟结果,具体数据及试验方法参见文献[7].

从图3可知,不同文献给出的风压系数平均值和均方根均存在一定差别,特别是风压系数均方根.本文计算的风压系数平均值和均方根值无论在正压区还负压区,均与风洞试验值存在一致性,表明湍流模型的选择和计算参数的设置均是可靠的.湍流积分尺度对风压系数有不同程度的影响(图3(a)).正压区风压系数平均值随湍流积分尺度增大而增大2%～5%,即湍流积分尺度对正压区风压系数平均值的影响很小.在负压区,随湍流积分尺度的增大,平均风压系数绝对值减小,侧面平均风压系数绝对值降低12%～17%,背面降低13%,即湍流积分尺度主要对侧面和背面风压系数的影响显著,这与文献[3]的结论一致.与文献[10]中City、Bristol、Monash、NAE和文献[7]的风洞试验结果相比,湍流积分尺度调整系数φ=0.4 时,平均风压系数与其结果较一致,尤其是侧面和背面.

(a) 2/3H高度处平均风压系数

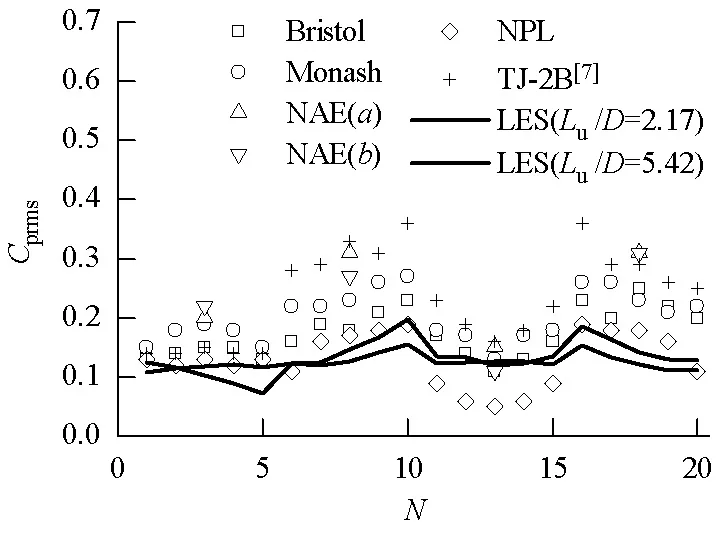
(b) 2/3H高度处风压系数均方根图3 湍流积分尺度对风压系数的影响Fig.3 Influence of turbulence integral lengths on wind pressure coefficients

图3(b)可知,无论是正压区还是负压区,风压系数均方根值均随湍流积分尺度的增大而降低,且角部降幅最大,这可能是受流体的分离与附着的影响.迎风面除角部显著降低外,其他测点风压系数均方根相差很小,侧面和背面最大降幅分别为15%和10%.湍流积分尺度调整系数φ=0.4时,模拟值与试验结果更一致,即湍流积分尺度的增大将降低风压脉动性.

综上分析可知,随湍流积分尺度的增大,除迎风面风压系数平均值较风洞试验结果略大外,其他部位均偏小,且风压系数均方根值降低,这与文献[1]的试验结果一致.分析其原因,从式(8)可知,增大湍流积分尺度,若保持湍流强度不变,湍动能的耗散率将降低.文献[4]指出,增大湍流积分尺度将减少小尺度的脉动运动量.Richardson[4]认为小尺度的脉动是将湍动能向热能的转变,所以湍动能耗散率的降低和小尺度脉动运动减少势必造成系统能量不平衡,要维持平衡将迫使湍动能增大,即提高耗散率.由式(7)可知,湍动能增大的物理表现是湍流强度的提高,由式(3)中的pij项可知,湍流强度的提高必须增大平均运动的变形率,平均运动的变形率向湍流脉动输入平均能量,这将导致平均速度减小,以致出现迎风面平均风压系数随湍流积分尺度的增大而略降现象(图3(a)).因湍流积分尺度增大导致湍流强度提高,文献[13]的研究指出,湍流强度的提高分流剪切流附着性提前出现,涡脱强度降低,空气夹带能力减弱,这将导致负压区的平均风压系数绝对值和风压系数均方根均减小(图3).侧面风压与分离流的附着、来流风速和湍流强度有关,背面风压受旋涡结构、旋涡分布等有关,受来流风速和湍流强度的影响很小.

3.3 气动力沿高度的变化

为研究湍流积分尺度对阻力的影响,计算了不同湍流积分尺度的测点层高度z处的平均阻力系数,见图4.

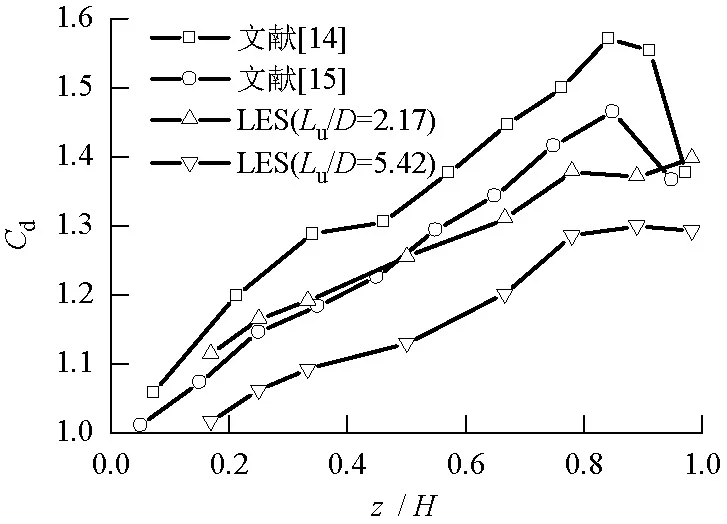
图4 层平均阻力系数沿高度变化Fig.4 Mean drag coefficient of the layer at different height

由图4可知:平均阻力系数沿高度的变化与文献[14]和文献[15]风洞试验结果基本一致,且模拟结果与文献[14]更接近，沿高度方向风速逐渐增大,平均阻力系数也逐渐增大，至0.85H处,顶部受三维流态的影响,其值出现降低现象[14]，相比风洞试验,数值模拟受三维流态的影响偏小,这可能是两者的边界条件不同所致；湍流积分尺度越大,平均阻力系数越小,且沿高度方向变化,降幅5%～10%,其原因是阻力包括迎风面来流风与壁面的碰撞和背面旋涡脱落产生的负压,湍流积分尺度的增大虽然使得迎风面风速略增,但背面分离流附着性增强,负压绝对值减小,以致阻力系数总体上表现为降低.

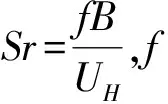
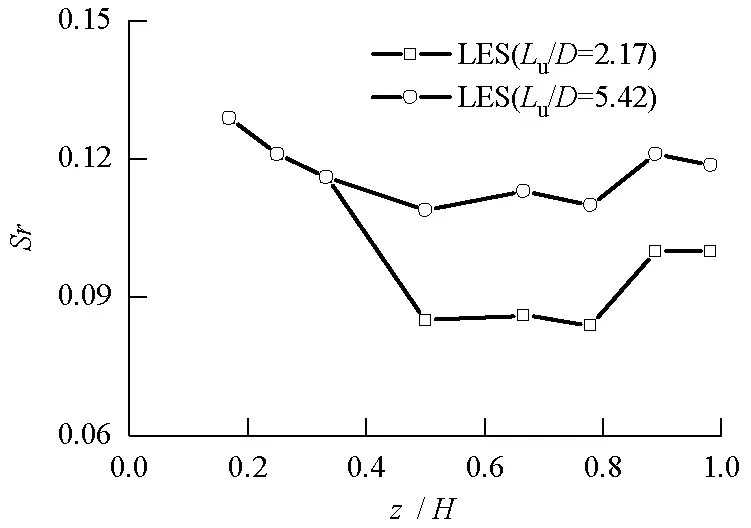
图5 斯托罗哈数(Sr)沿高度变化Fig.5 Strouhal number at different height

由图5可知,湍流积分尺度并没有改变Sr沿高度变化趋势.湍流积分尺度越大,Sr沿高度增大相对越小,0.4H高度以下两者相差很小,0.4H至0.9H其值降低了约30%,0.9H以上其值降低了约20%,可见湍流积分尺度越大,涡脱落频率越低.

结合图4和图5可知：在1/3H以下,湍流积分尺度对测点层平均阻力系数和斯托罗哈数的影响不明显;当高度大于1/3H时,其影响越来越明显,这是因为风速沿高度逐渐增大,底部虽然湍流强度大,但风速偏小.可见湍流积分尺度对高层建筑风荷载有明显的影响,且风速越大,影响越显著.

3.4 流线分析

为获得不同湍流积分尺度下的绕流特征,利用CFD的优势,获得2/3H高处x-y平面的流线图;为重点研究细部绕流特性,选取了关键部位流线图进行分析,见图6.

由图6可知:

与φ=1相比,当φ=0.4时,迎风面剪切分离流距侧面越远,旋涡的尺度更大,侧面和背面均存在大尺度旋涡,表现为较强的涡脱性,尾流宽度大;当φ=1时,虽然旋涡的尺度小,但尾流宽度小,剪切分离流在侧面和背面均表现较好的附着性.

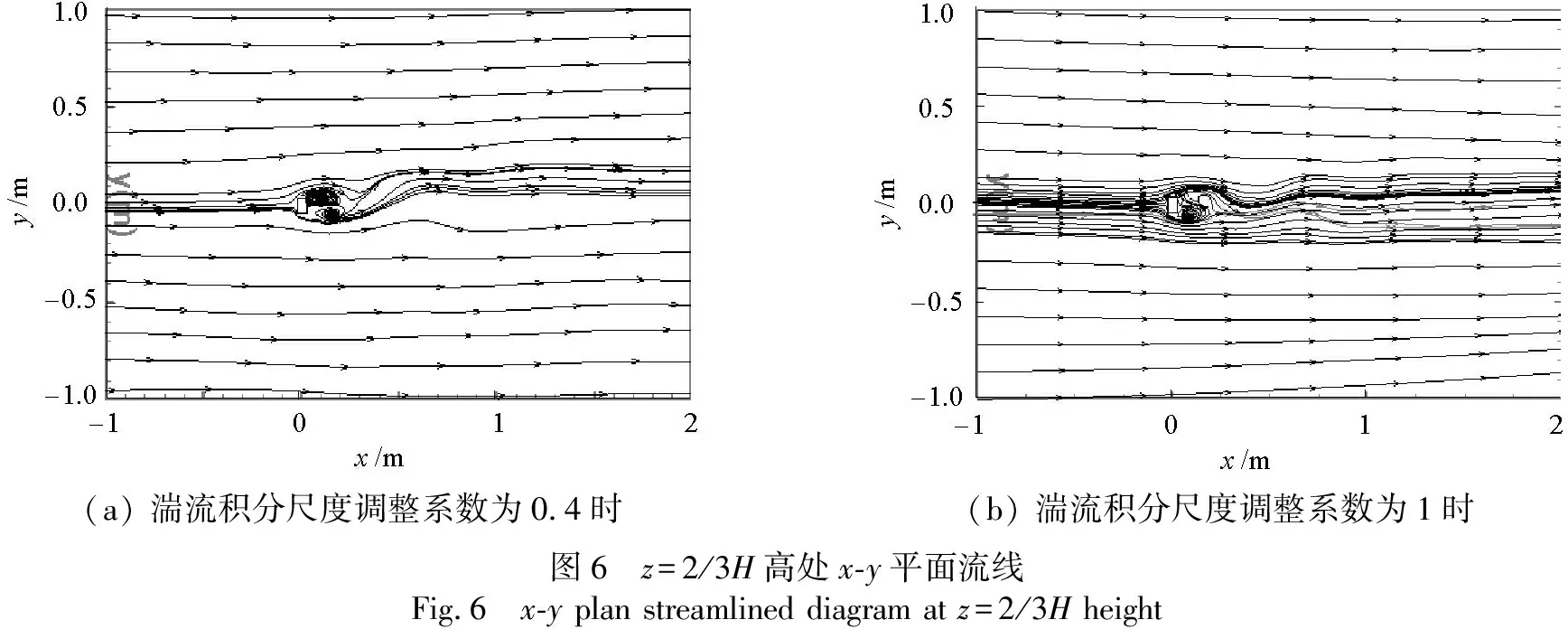
(a) 湍流积分尺度调整系数为0.4时(b) 湍流积分尺度调整系数为1时图6 z=2/3H高处x-y平面流线Fig.6 x-y plan streamlined diagram at z=2/3H height

3.5 频谱比较与分析

以下进一步研究湍流积分尺度对基底力矩谱的影响,见图7(图中:横坐标为斯托罗哈数;纵坐标中σMz、σMx和σMy分别为基底扭矩均方根、基底顺风向弯矩均方根和基底横风向弯矩均方根,SMz(f)、SMx(f)和SMy(f)分别为基底扭矩功率谱密度、顺风向基底弯矩功率谱密度和横风向基底弯矩功率谱密度.

由图7(a)可知，随湍流积分尺度增大,基底扭矩谱的峰值减小,但降幅很小，频带明显变窄,高频段幅值降低,原因是增大湍流积分尺度,伴随小尺度脉动运动量减少[4],附着提前出现(见图6),这不但导致紊流对扭矩的贡献降低,而且改变了能量在各频域带的分布,谱频带变窄.

由图7(b)可知，顺风向基底弯矩谱峰值不明显,谱频带较宽,不同湍流积分尺度的顺风向弯矩谱发展趋势基本一致，湍流积分尺度越大,高频段幅值越低,这是由于湍流积分尺度的增大导致背面旋涡脱落强度降低所致.

由图7(c)可知，随湍流积分尺度增大,横风向基底弯矩谱峰值基本不变,但涡脱频率降低、高频段的幅值减小,低频段幅值略显升高趋势,原因是随湍流积分尺度的增大,大尺度的脉动运动相对增多和小尺度脉动减少[4].

Richardson[4]认为:

大尺度湍流脉动是蓄能池,小尺度湍流脉动将湍动能转变成热能进行耗散,即能量主要集中在大尺度的湍流脉动上,所以低频段出现能谱升高、高频段幅值降低的现象;其次,横风向基底弯矩主要来源于漩涡脱落诱发的气动力,紊流对其也有一定贡献.随湍流积分尺度的增大,湍流强度增大,侧面风压系数绝对值减小也有关.

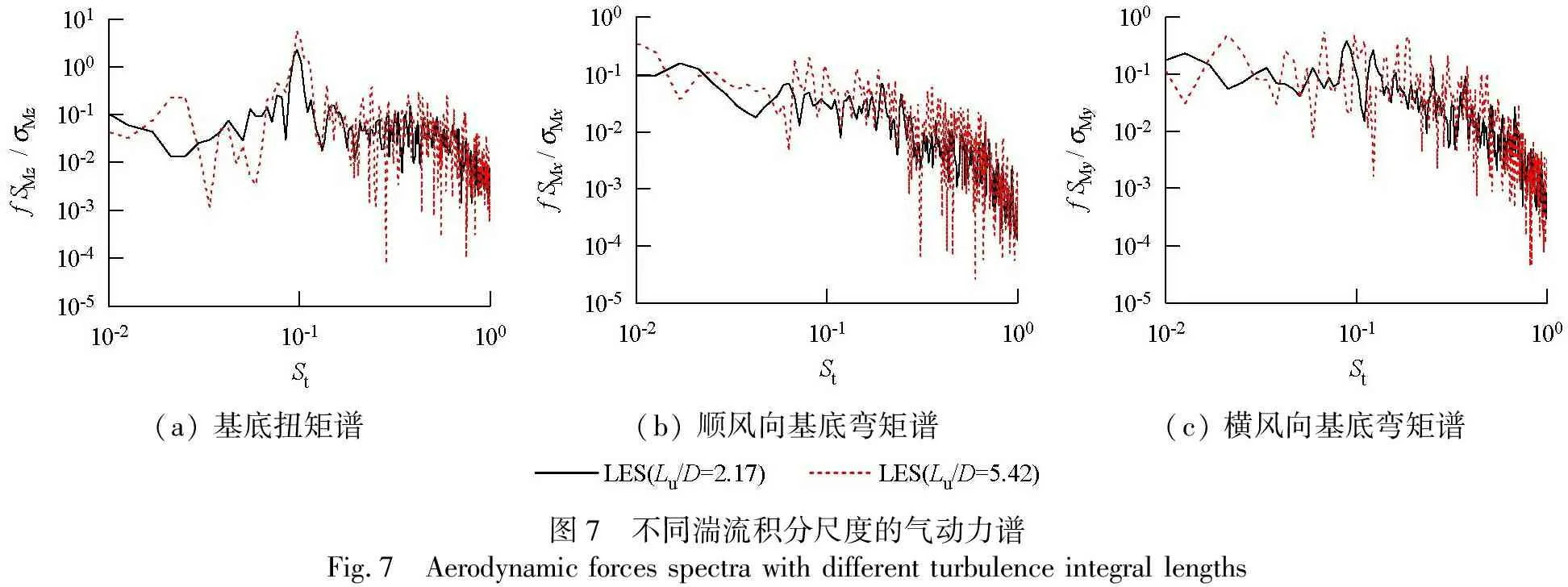
(a) 基底扭矩谱(b) 顺风向基底弯矩谱(c) 横风向基底弯矩谱图7 不同湍流积分尺度的气动力谱Fig.7 Aerodynamic forces spectra with different turbulence integral lengths

3.6 相关性

相关系数是两个随机变量存在线性依赖的一种测度,湍流积分尺度对气动力相关性的影响是一个值得重视的问题,本文定义模型高度方向上任意两层气动力时程或同一水平面上模型表面任意两点压力时程r、s的相关系数为

(16)

式中:r=1,2,…,R；s=1,2,…,n;CoVF(zr,zs)为高度zr和zs风力协方差;σF(zr)和σF(zs)和分别为高度zr和zs的风力根方差;n(或R)为模型测点层数.

3.6.1水平相关性

以第五层测点(即H=406 mm)为例进行风压水平相关性分析,按照式(11)计算迎风面、上侧面和背面各自面内中间测点与其它测点的风压相关系数,见图8.图中：x为距中点的距离,迎风面下部为负,上部为正;侧面左边为负,右边为正;背面上部为负,下部为正;d为测点所在面的边长.由图8可知：两测点的距离越大,风压相关系数越小;相同距离测点相关系数值表现为迎风面的最大,背风面最小；相关系数随湍流积分尺度增大而减小,且测点间距越大,差异越明显；随测点距离的减小,不同湍流积分尺度计算得到的相关系数的差值呈现降低趋势,且不同的面存在较明显差异.

迎风面湍流积分尺度小时,风压水平相关曲线表现良好的对称性(图8(a)),这表明旋涡分布更均匀.随湍流积分尺度的增大,风压水平相关系数最大降幅为4.5%, 可见湍流积分尺度对迎风面风压相关性的影响很小.侧面风压水平相关曲线表现为湍流积分尺度越小,风压水平相关曲线对称性越差,尤其在下风向更突出,甚至出现骤降现象.随湍流积分尺度的增大,侧面上风向风压水平相关系数的增幅很小,但下风向增幅达到15%～25%(图8(b)).这是由于湍流积分尺度小时湍流强度也小,侧面旋涡脱落性强,风压脉动性强(图3),以致风压相关性差，且由于侧面上下风向旋涡尺度和旋涡强度不同(图6),所以脉动风压不同步,以致相关性较差,甚至出现骤降.

由图8(c)可知:不同湍流积分尺度背面风压相关系数相差5%～10%,这与背面风压与背面旋涡的尺度、结构及分布的影响有关,受来流风速和湍流强度的影响相对较小.虽然增大湍流积分尺度会导致湍流强度增大,但湍流强度的变化对背面风压的影响很小.

可见风压水平相关性受湍流积分尺度的影响较大,由于湍流积分尺度的增大,湍流强度增大,侧面分离剪切流在侧面提前附着,导致侧面和背面的平均风压系数绝对值和脉动值均降低,风压的相关系数提高.

3.6.2竖向相关性

以第4层测点为基准,计算不同湍流积分尺度时各测点层升力相关系数(RL)和阻力相关系数(RD),见图9.

由图9可知:在0.8H以下,不同湍流积分尺度的测点层升力和阻力相关系数的差值很小,可不考虑其对相关性的影响;随高度的增加,湍流积分尺度的影响逐渐增大,值得注意的是层升力相关系数的变化很小,层阻力相关系数的增幅颇为明显,尤其是靠近建筑物顶部,最大增幅约50%,这可能受顶部三维流态的影响所致[14].虽然湍流积分尺度对0.8H高度以上的层阻力相关系数影响明显,但影响范围有限,可以认为湍流积分尺度对气动力的竖向相关性的影响很小,建议不予考虑.

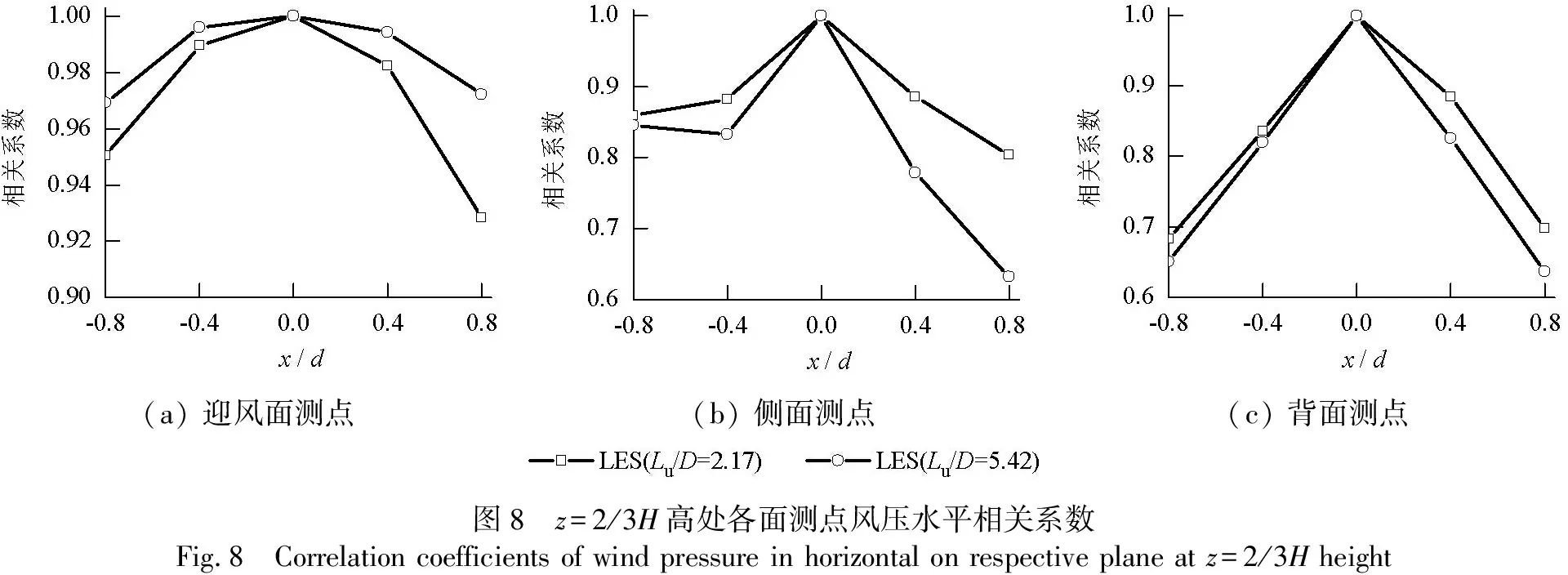
(a) 迎风面测点(b) 侧面测点(c) 背面测点图8 z=2/3H高处各面测点风压水平相关系数Fig.8 Correlation coefficients of wind pressure in horizontal on respective plane at z=2/3H height

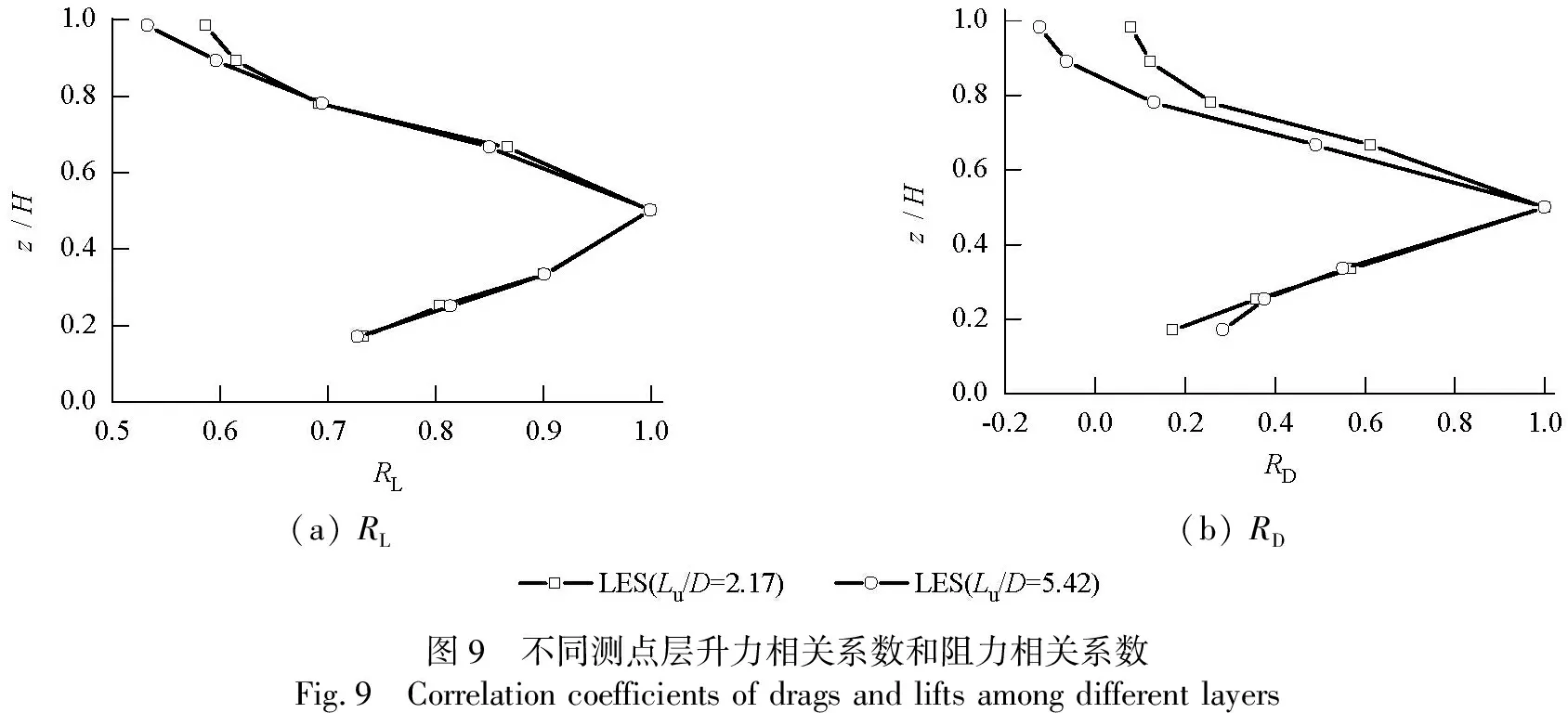
(a) RL(b) RD图9 不同测点层升力相关系数和阻力相关系数Fig.9 Correlation coefficients of drags and lifts among different layers

4 结 论

本文采用大涡模拟的方法,在入口处保持速度、湍流强度、湍动能不变的前提下,研究了湍流积分尺度对高层建筑风荷载的影响,得到以下结论:

(1) 增大湍流积分尺度会使得各面的风压系数均方根均降低,迎风面平均风压系数略增,侧面和背风面平均风压系数绝对值均减小.湍流积分尺度为k1时的模拟结果与试验值更吻合.

(2) 随湍流积分尺度的增大,平均运动的变形率向湍流脉动输入平均能量,导致平均风速略降，湍流强度略增;横风向漩涡脱落频率减小;基底扭矩谱和横风向基底弯矩谱的峰值及高频段谱幅值均呈降低趋势.B类地貌湍流积分尺度调整系数为0.4时,计算精度更高,计算结果与文献实验值更吻合.

(3) 随湍流积分尺度的增大,测点层阻力系数平均值和斯托罗哈数均沿高度方向呈降低趋势,高度1/3H以下时表现不明显,但1/3H以上时影响逐渐增强.

(4) 湍流积分尺度的增大,会导致湍流强度增大,侧面和背面剪切分离流附着性提前出现,旋涡脱落能力减弱,表现为斯托罗哈数值降低，负压区风压得以恢复,风压水平相关性增强,但对竖向风压相关性的影响很小.

[1] 卢占斌,魏庆鼎. 网格湍流CAARC模型风洞实验[J]. 空气动力学学报,2001,19(1): 16-23.

LU Zhanbin, WEI Qingding. An experiment on a CAARC model in grid turbulent flow[J]. Acta Aerodynamica Sinica, 2001,19(1): 16-23.

[2] JR F L H, KAREEM A, SZEWCZYK A A. The effects of turbulence on the pressure distribution around a rectangular prism[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 77-78(98): 381-392.

[3] NAKAMURA Y, OZONO S. The effects of turbulence on a separated and reattaching flow[J]. Journal of Fluid Mechanics, 1987, 178: 477-490.

[4] LI Q S, MELBOURNE W H. The effects of large scale turbulence on pressure fluctuations in separated and reattaching flows[J].Journal of Wind Engineering and Industrial Aerodynamics.1999, 83(1/2/3): 159-169.

[5] Huang S H, Li Q S, Wu J R. A general inflow turbulence generator for large eddy simulation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(10): 600-617.

[6] 张兆顺,崔桂香,许晓春. 湍流大涡模拟的理论与应用[M]. 北京:清华大学出版社,2005: 4-42.

[7] 罗盘. 基于标准模型的风洞试验研究[D]. 上海:同济大学土木工程学院,2004.

[8] TAMURA Y, OHKUMA T, KAWAI H, et al. Revision of AIJ recommendations for wind loads on buildings[C]∥Structures Congress. Nashville: [s.n.], 2004: 1-10.

[9] LAKEHAL D. Application of thek-εmodel to flow over a building placed in different roughness sublayers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 73(1): 59-77.

[10] MELBOURNE W H. Comparison of measurements of the CAARC standard tall building model in simulated model wind flows[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1980， 6(1): 73-88.

[11] OBASAJU E D. Measurement of forces and base overturning moments on the CAARC tall building model in a simulated atmospheric boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics,1992, 40(2): 103-126.

[12] 杨有根. 高层建筑的抗风实测分析与大跨度屋盖的风致响应研究[D]. 长沙:湖南大学,2007.

[13] 苏万林,李正农. 湍流对超高层建筑风压幅值特性影响的研究[J]. 地震工程与工程振动,2016,36(3): 118-126.

SU Wanlin, LI Zhengnong. Research of turbulent effects on characteristics of wind pressure amplitude on tall buildings[J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(3): 118-126.

[14] 唐意. 高层建筑弯扭耦合风致振动及静力等效风荷载研究[D]. 上海:同济大学土木工程学院,2006.

[15] 陈建兰. 矩形截面高层建筑风荷载试验研究[D]. 武汉:华中科技大学,2005.