基于粒子群算法的3D印花网版对位的移动平台误差补偿

李 培，李培波，谢 瑶，孙以泽

(东华大学 机械工程学院，上海 201620)

随着丝网印刷技术的发展，高精度3D印花技术应运而生。 高精度3D印花的图案厚度要求在0.8 mm以上，需多块网版叠印、套印数十次，因此多块网版的对位成为一个难题，也是决定印花质量的关键。传统的人工对版已不能满足要求，对版机在一定程度上解决了这一问题。三自由度移动平台应用在对版机上可实现网版的对位，但由于几何参数误差、动态误差等因素的存在，导致对版机的对位精度往往不能满足实际要求。 对位精度主要由三自由度移动平台的精度决定，因此需对三自由度移动平台进行误差分析及补偿，以提高对位精度。

粒子群优化算法可用于寻找多参数非线性模型(目标函数)的全局极值点，其步骤为：(1)初始化结构参数和粒子群算法参数; (2)根据目标函数计算适应度值; (3)计算个体极值和全局极值; (4)比较适应度值的大小; (5)更新粒子速度和位置，寻找更优解，直到完成所设定的迭代次数[1-2]。

本文以3D印花网版对位的综合误差为目标函数，利用粒子群优化算法寻找最优解，减少综合误差，提高对位精度。

1 误差模型

建立并联机构输出误差模型的方法主要有矢量法[3-4]和误差独立作用原理法[5]。对滚珠丝杆的误差研究多以单驱动机构为对象，采用矩阵法得到末端执行构件的输出误差模型[6]。 本文研究的三自由度移动平台为多滚珠丝杆并联机构，借鉴上述方法，对其建立输出误差模型，并在此基础上建立3D印花网版对位的综合误差模型。

1.1 三自由度移动平台的结构

三自由度移动平台的结构如图1所示。 该机构由3台驱动电机驱动，驱动电机固定在定平台上，通过联轴器与滚珠丝杠连接，并通过丝杠螺母驱动滑座移动。 动平台与4个交叉滚子轴承连接，滑座分为上中下3部分，上面部分与交叉滚子轴承连接，下面部分固定在定平台上。3台电机的组合驱动可以使动平台实现两个方向的平移以及在其平面内的旋转，因此，该机构具有三个自由度。

1.2 等效结构简图

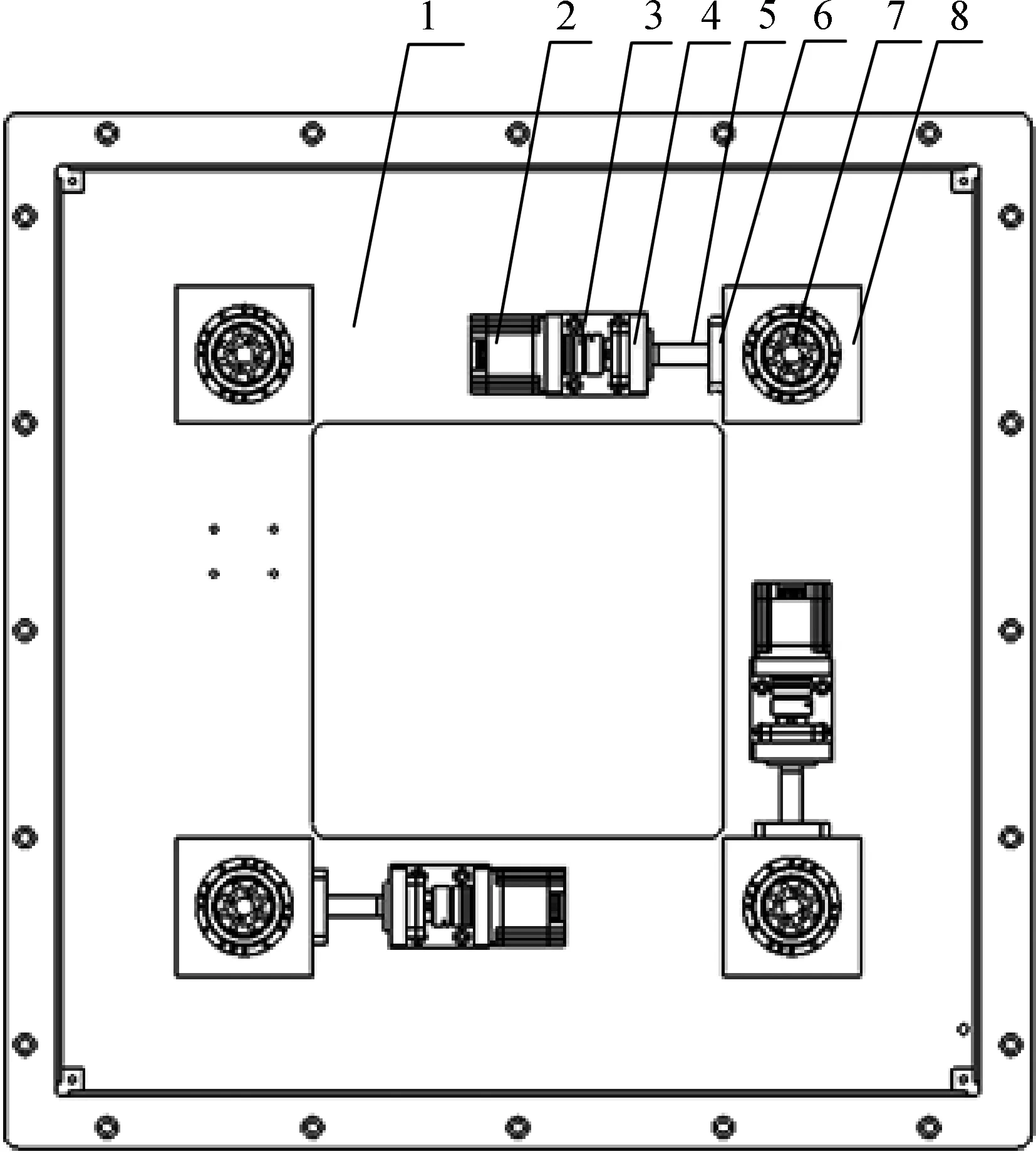
1—定平台; 2—驱动电机; 3—联轴器; 4—丝杆支座; 5—滚珠丝杠; 6—丝杠螺母; 7—交叉滚子轴承; 8—滑座图1 三自由度移动平台结构图Fig.1 Structure diagram of three degrees of freedom mobile platform

建立坐标系O-xyz，其中xOy面固定在定平台上。 该三自由度移动平台具有沿x轴方向和y轴方向平移的自由度，还有绕z轴旋转的自由度。 电机驱动滚珠丝杆，使丝杆螺母在丝杆上移动，同时带动动平台，因此，该驱动机构可以看做可伸缩的驱动杆或可移动的滑块。 将3台驱动电机分别旋转180°，对于相同的动平台位置和姿态，丝杆螺母的位移相同，仅仅是电机的旋转方向相反。 综上所述，该三自由度移动平台的等效结构简图如图2所示。

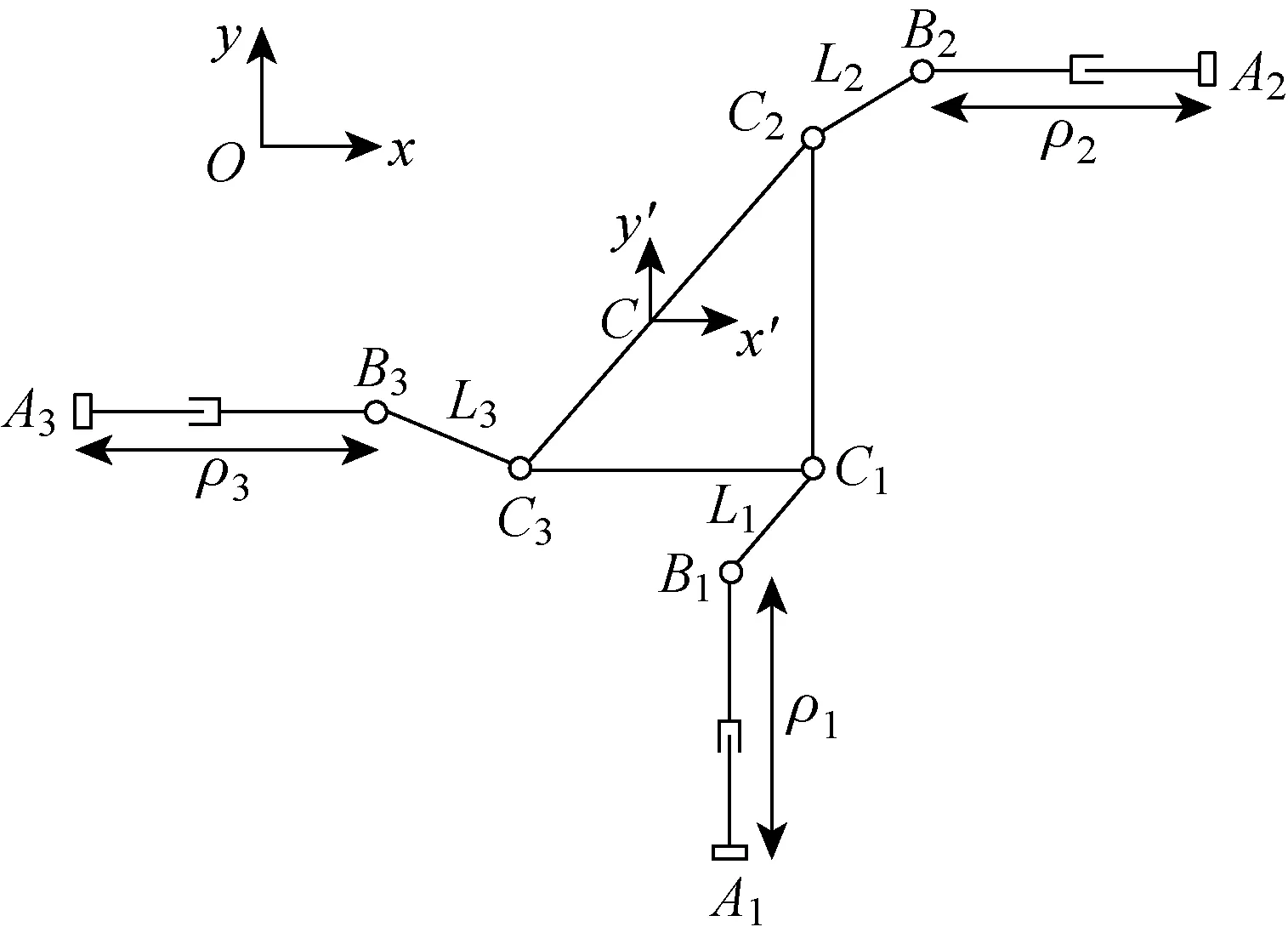
图2 三自由度移动平台等效结构简图Fig.2 Equivalent structure diagram of three degrees of freedom mobile platform

1.3 三自由度移动平台的误差模型

如图2所示，建立坐标系Oxy和Cx′y′，其中Oxy面固定在定平台上，Cx′y′面固定在动平台上。 驱动杆首端(滑块初始位置)为Ai点(i=1，2，3)，动平台上安装孔的位置为Ci点(i=1，2，3)，C1、C2、C33点组成等腰直角三角形，其外接圆圆心为坐标原点C，x′轴平行于C3C1，y′轴平行于C1C2。 等腰直角三角形C1C2C3的直角边长度为a，即动平台上安装孔间距，则C1、C2、C33点在坐标系Cx′y′中的坐标为

(1)

动平台的位置及姿态可用式(2)矩阵描述。

(2)

式中：xC、yC为C点在固定坐标系Oxy中的坐标;θ为x轴与x′轴之间的夹角。

坐标系Oxy到坐标系Cx′y′的齐次变换矩阵R可表示为

(3)

根据式(3)，点Ci在坐标系Oxy中的坐标(xCi，yCi)可写成：

(4)

(5)

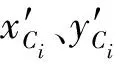
根据各点坐标之间的关系，点Ci在坐标系Oxy中的坐标(xCi，yCi)也可写成：

xCi=xAi+ρicosαi+Licosβi

(6)

yCi=yAi+ρisinαi+Lisinβi

(7)

式中：xAi、yAi为点Ai在坐标系Oxy中的坐标;ρi为驱动杆AiBi的长度，即驱动进给量;αi为驱动杆AiBi与x轴之间的夹角;Li为连杆BiCi的长度;βi为连杆BiCi与x轴之间的夹角。

由式(4)～(7)得：

(8)

(9)

对式(8)和(9)进行微分并整理得：

(10)

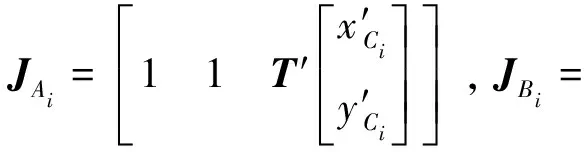
(12)

代入式(12)得：

JAδP=JBδe

(13)

则该三自由度移动平台的输出误差模型为

(14)

1.4 3D印花网版对位的综合误差模型

3D印花网版的4个角均有一个校准点，呈中心对称分布。 网版对位的基本原理是：计算机采集任意对角的两个校准点图像，分析得到其位置信息，并控制三自由度移动平台将两个校准点移动到指定位置，实现网版的对位。 校准点的位置准确度决定了网版的对位精度。 校准点的理论位置与实际位置如图3所示。

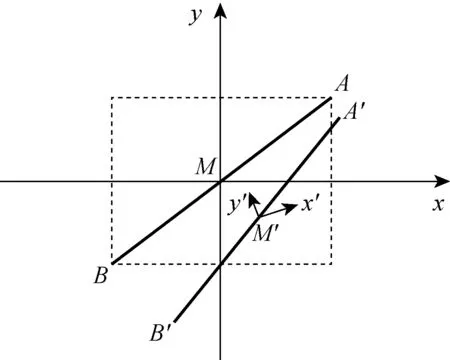
图3 校准点的理论位置与实际位置Fig.3 Theoretical position and actual position of calibration point

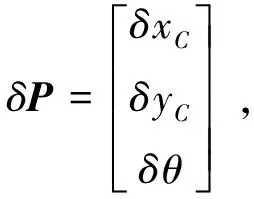
(15)

A点和B点在坐标系Mxy中的坐标分别为(b/2，c/2)和(-b/2，-c/2)，其中，b、c分别为对角两校准点之间的距离在x轴方向和y轴方向上的分量。则A′点和B′点在坐标系Mxy中的坐标为

(16)

(17)

则3D印花网版对位的综合误差ΔP可表示为：

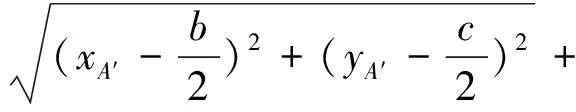
(18)

2 三自由度移动平台的运动学标定

运动学标定是指通过测量系统的输出量辨识出误差模型中各几何参数的实际值。 常用的并联机构标定方法有外部标定法和自标定法两种，其中，自标定法根据标定中采用的运动学模型的不同，又可分为基于逆解的标定和基于正解的标定[7-9]。 本文采用基于逆解的自标定法得到三自由度移动平台几何参数的实际值。

2.1 三自由度移动平台的逆解模型

将式(8)和(9)移项后两边平方再相加消除变量βi(i=1，2，3，下同)，得到运动学方程组为

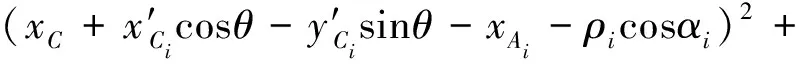
(19)

将式(19)整理得：

(20)

解得：

(21)

式中：

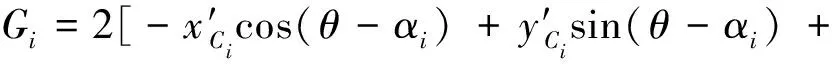
由式(21)可知，每一个驱动杆长(即驱动进给量)有两个解，所以在给定动平台位姿的情况下，可以求出8组驱动进给量的解，对应着机构的8种控制模式。 经分析可知，本文所述机构的等效逆解模型为

(22)

2.2 标定方法及结果

本文应用激光跟踪测量法测量动平台的实际位姿，在滑座上安装位移传感器，测量滑座的实际位移，得到驱动进给量的实际值。

手动模式下使动平台处于多个不同的位姿，通过激光跟踪系统以及位移测量系统测得三自由度移动平台的多组位姿实际值以及驱动进给量实际值。 由式(22)可知，共有18个未知量，而测得的每组数据可列3个方程，因此，至少需要测量6组数据才能求解出所有未知量。 测得的数据如表1所示，将数据代入逆解模型，应用最小二乘法解得各几何参数实际值，如表2所示。

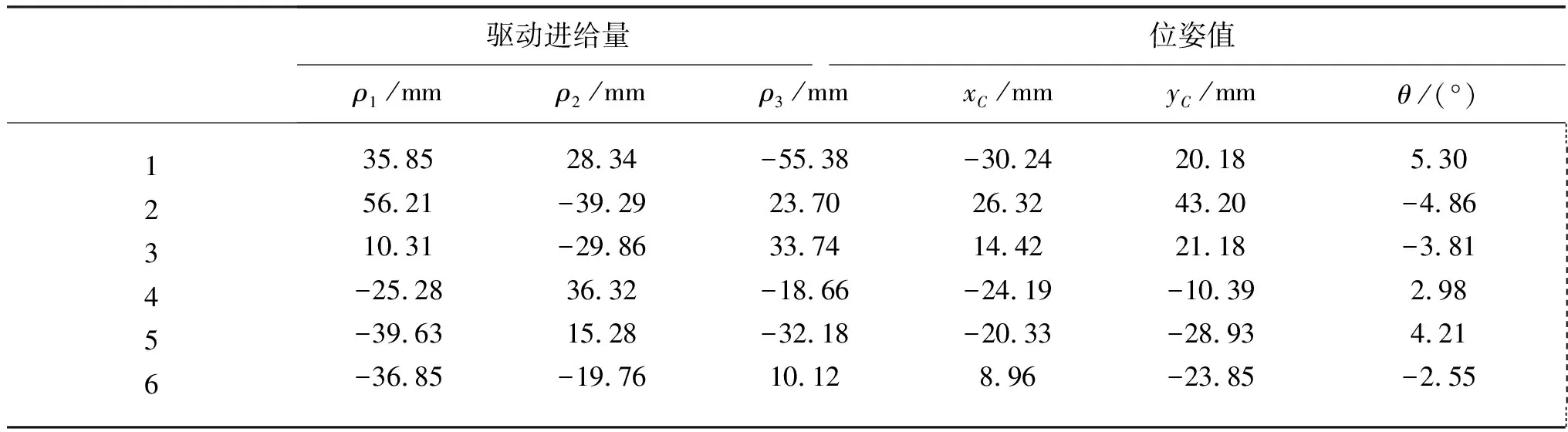
表1 驱动进给量和动平台位姿测量值Table 1 Measured values of the drive feed rates and the position and pose of the mobile platform

表2 几何参数实际值Table 2 Actual values of the geometric parameters

3 基于粒子群优化算法的误差补偿

3.1 粒子群优化算法

由式(18)可知，3D印花网版对位的综合误差模型包含驱动杆长误差δρi(i=1，2，3)，因此可给驱动进给量一修正量Δρi，使驱动杆长误差为δρi+Δρi，以减小综合误差。 综合误差模型是一个多输入的非线性模型，本文将误差补偿转化为多参数组合优化问题，通过粒子群优化算法寻优各驱动杆参数，以补偿误差。

设定三自由度移动平台3根驱动杆长度的取值范围为ρimin≤ρi≤ρimax(i=1，2，3)，即粒子的搜索空间。 算法随机产生的粒子在空间内飞行搜索，并根据自己和同伴的飞行经验调整自己的飞行。 每个粒子在飞行过程中搜索到的最优位置为个体极值点，整个群体搜索到的最优位置为全局极值点，每个粒子通过个体极值点和全局极值点更新自己，经过多次迭代，找到最优解[10]。 粒子按式(23)和(24)更新自己的速度和位置。

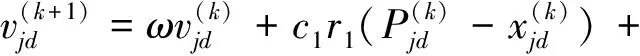
(23)

(24)

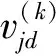
每个粒子都有一个由被优化的目标函数决定的适应度值，由它对粒子进行评价。 本文以3D印花网版对位的综合误差模型(式(18))为目标函数，结合式(14)、(16)、(17)，并将δρi用δρi+Δρi代替，得到只含有参数Δρi的目标函数。

3.2 仿真分析

粒子群优化算法的参数设定如下：粒子总数m=40，学习因子c1=c2=2，惯性系数ω=0.8。 综合误差优化值与迭代次数的关系如图4所示。

图4 综合误差优化值与迭代次数的关系图Fig.4 Relationship between the optimal value of the synthetic error and the number of iterations

由图4可知，当迭代次数n≥4次时，综合误差趋于稳定，因此本文选取迭代次数n=4。 至此，粒子群优化算法的参数设置完毕，机构几何参数采用通过运动学标定得到的实际值。 利用Matlab软件进行仿真，可得到各支链驱动进给量的修正量和综合误差的优化值，分别如图5和6所示。 为了更直观地观察修正量和补偿效果，本文假定动平台的旋转角θ=5°，驱动进给量ρ1=ρ2=ρ3。

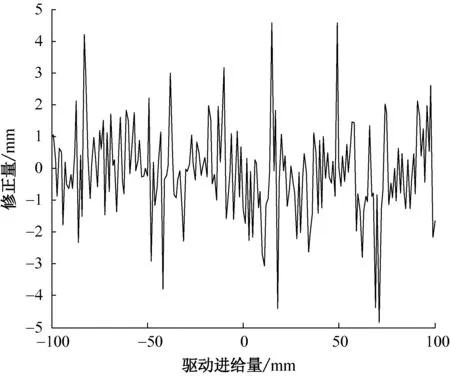
(a)支链1

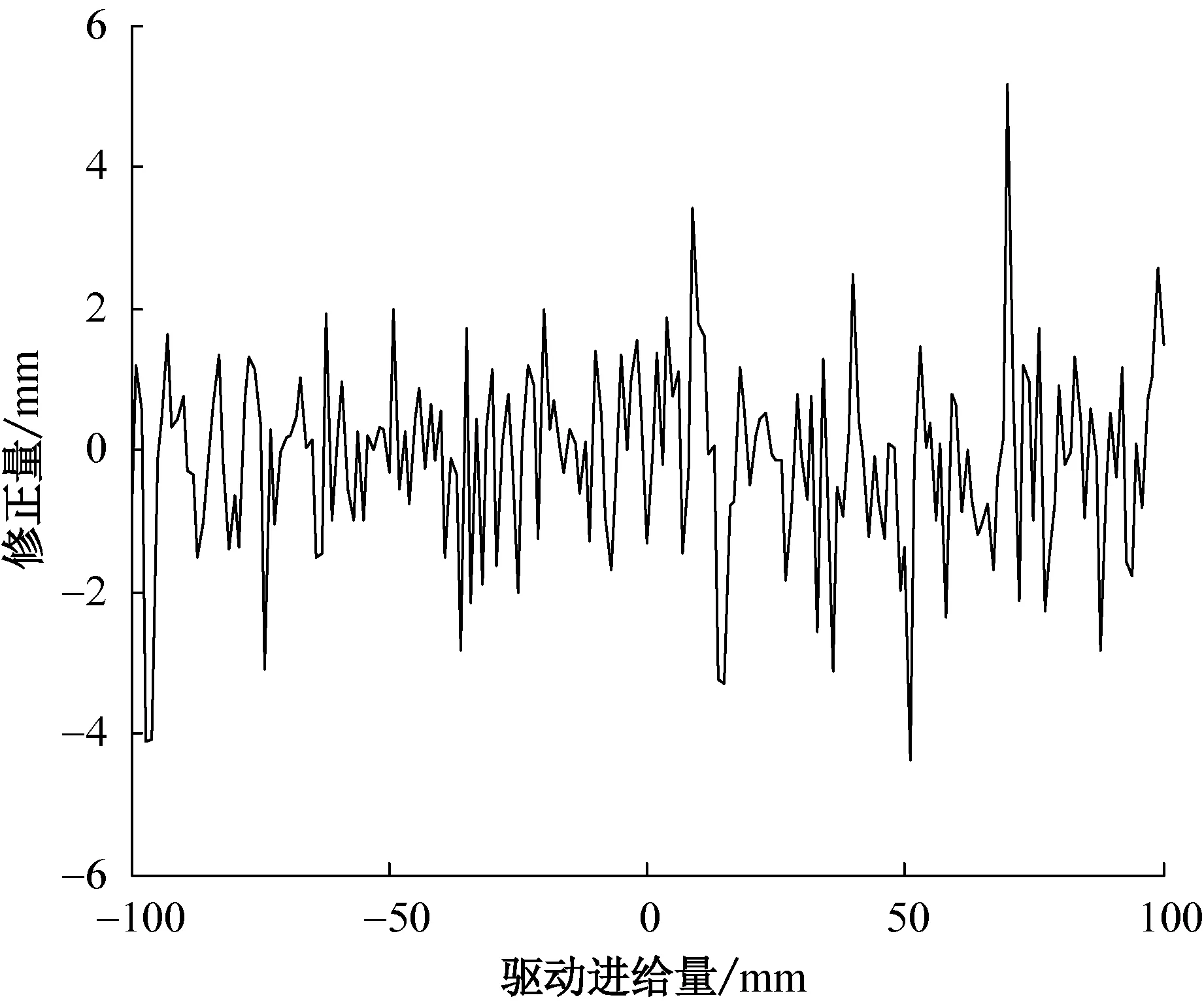
(b)支链2

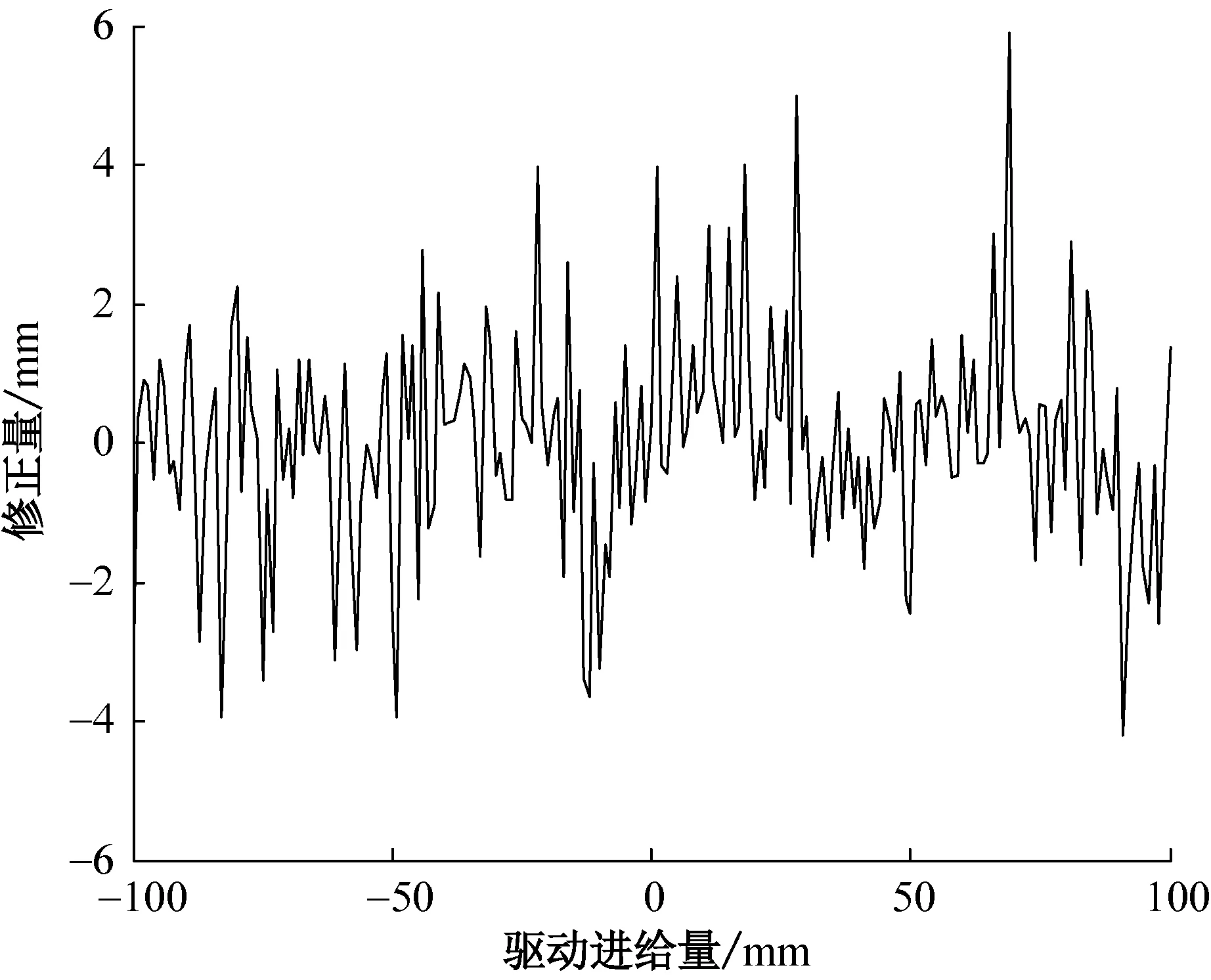
(c)支链3图5 各支链驱动进给量的修正量Fig.5 Corrected values of each branch drive feed rate

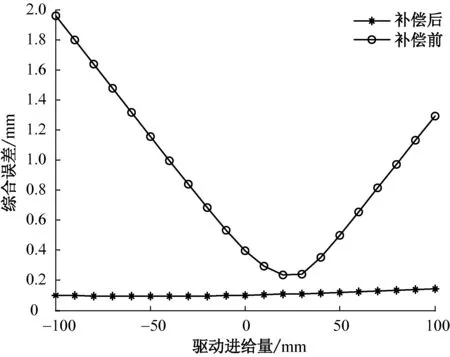
图6 综合误差的补偿效果图Fig.6 Compensating effect diagram of the synthetic error

由图5可知：对于不同的驱动进给量，3D印花网版对位的综合误差不同，因此进给量的修正量也不同; 3个支链驱动进给量的修正量范围均为-6～6 mm，但各不相同。

由图6可知：补偿前，3D印花网版对位的综合误差范围为0.21～1.96 mm，补偿后，综合误差保持在0.10 mm左右，即利用粒子群优化算法补偿误差的效果是显著的; 对于不同的驱动进给量，补偿后的综合误差接近于一恒定值。由此，一套网版对位的综合误差几乎相同，这可极大地减小对位误差引起的印刷质量问题。

3.3 试验验证

根据本文所述方法，改进对版机的控制方式，并使用改进后的对版机进行试验，以验证粒子群优化算法对三自由度移动平台对位误差的补偿效果。 对于3D印花而言，一套网版对应着一个完整的图案，印刷前将它们依次放置在对版机上进行对位，如图7所示。 对位完成后，将它们依次放置在印花机上进行印刷，每块网版印刷一层子图案。 从第二块网版开始，每块网版印刷结束后，将图案放置在显微镜下观察，并用测量装置测量相邻两层子图案之间的最大偏移量，即最大误差。 按照上述试验内容完成3组试验，驱动进给量的修正量和最大偏移量的测量结果如表3所示。

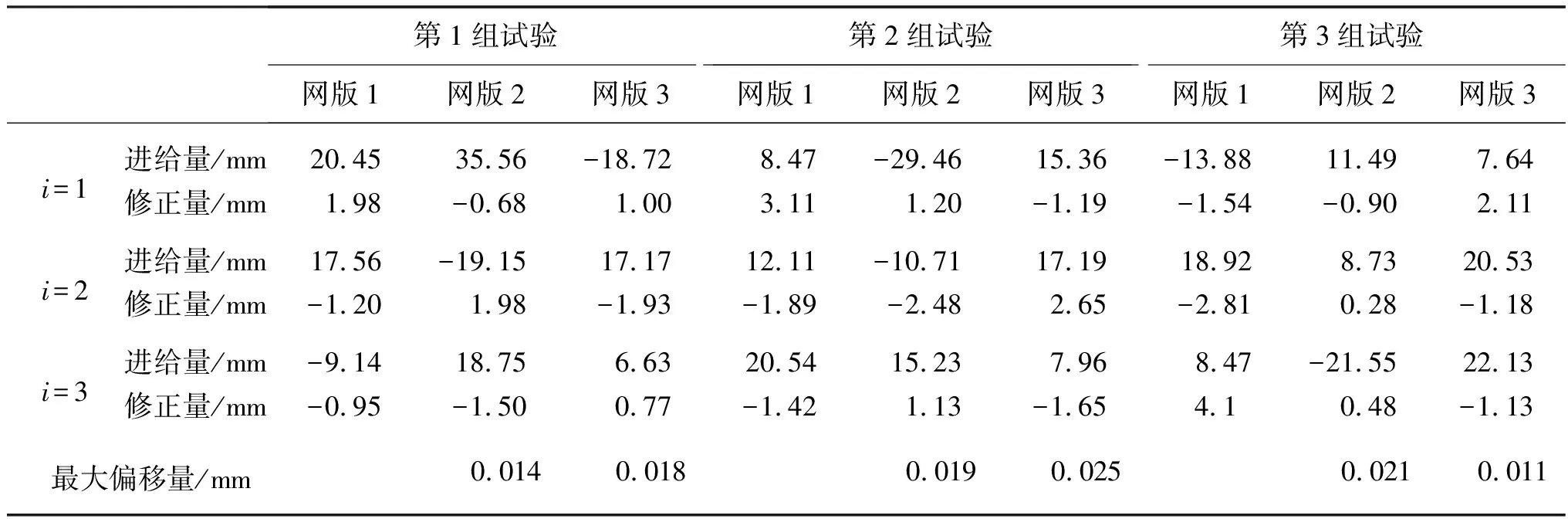
表3 驱动进给量的修正量和最大偏移量的测量结果Table 3 Corrected values of drive feed rates and measured result of maximum offset

由表3可知，利用改进后的对版机进行网版对位，并将网版放置在印花机上印刷，得到的印刷图案的相邻两层子图案之间的最大偏移量不超过0.03 mm，精度完全符合实际要求，与本文的仿真结果基本吻合。

4 结 语

本文为提高对版机的对位精度，对其关键机构——三自由度移动平台进行了误差分析与补偿。 首先建立了动平台的输出误差模型以及3D印花网版对位的综合误差模型。 在误差模型的基础上，利用粒子群优化算法进行误差补偿，该方法使用的几何参数值是通过运动学标定得到的实际值。 仿真的结果表明：进给量的修正量范围为-6～6 mm; 补偿前，综合误差范围为0.21～1.96 mm，补偿后，综合误差保持在0.10 mm左右。最后通过试验验证了粒子群优化算法对误差的补偿效果，试验结果与仿真结果基本吻合。因此，利用粒子群优化算法进行误差补偿，可明显减少3D印花网版对位的误差，使对版机精度符合实际要求。

参 考 文 献

[1] 谢平，杜义浩，田培涛，等. 一种并联机器人误差综合补偿方法[J]. 机械工程学报，2012，48(9): 43-49.

[2] 孔凡国，黄伟.基于粒子群算法的并联机构结构参数优化设计[J].机械设计与研究，2006，22(3)：16-18.

[3] 陈修龙，赵永生，邓昱. 新型并联机器人坐标测量机误差建模与仿真[J]. 计算机集成制造系统，2008，14(3): 477-486.

[4] GONG J，SHI W，SONG X. Analysis and compensation of the tip pose error in 6-PSS parallel mechanism[J]. Metalurgia International，2013，18(4): 264-267.

[5] 李兴山，蔡光起. 三自由度混联机床的机构误差分析与仿真[J]. 组合机床与自动化加工技术，2011(3): 19-22.

[6] 孙先锋，阎开印，丁国富，等. 滚珠丝杠综合误差对机床定位精度的分析[J]. 机械，2008，35(11): 45-47.

[7] 刘红军，龚民，赵明扬. 一种四自由度并联机构的误差分析及其标定补偿[J]. 机器人，2005，27(1): 6-9.

[8] SUN X Y，XIE Z J，SHI W K，et al. Error analysis and calibration of 6-PSS parallel mechanism[J]. Computer Integrated Manufacturing Systems，2012，18(12): 2659-2666.

[9] MAJARENA A C，SANTOLARIA J，SAMPER D，et al. Kinematic calibration of a 2-DOF spatial parallel mechanism[C]// American Institute of Physics Conference Series. 2012: 233-241.

[10] 潘峰，陈杰，辛斌，等. 粒子群优化方法若干特性分析[J]. 自动化学报，2009，35(7): 1010-1016.