融合主体偏好的铁路全生命周期指标评价

李彦瑾，罗 霞，朱 颖

(1. 西南交通大学 交通运输与物流学院，四川 成都 610031；2. 中铁二院集团有限责任公司，四川 成都 610031)

0 引 言

目前，我国已逐渐改变铁路项目完全由政府投资主导的局面，采用项目法人制，通过市场化运作实现全生命周期的规划、建设与管理。由于铁路项目是一个多主体参与、多阶段关联的综合复杂系统，为了提高工程项目投资的经济回报率，实现可持续发展的目标，规避各类风险，需从整体出发提出一套更好地衡量与评价铁路项目全生命周期的新型指标体系。

但是，现有全生命周期理论在工程领域的研究仍处探索阶段，理论支撑较少。对铁路项目的评价方法研究也主要集中在：铁路选线设计和安全运营评价两方面。在选线设计上：A. V. MOHAN等[1]、XIE Xiaoling等[2]等利用三维GIS技术对铁路工程设计环节进行仿真，再通过BIM平台对该线路全生命周期的经济效益进行评估；Y. HASSAN等[3]、SONG Tong等[4]等则在欧美发达国家高铁成网、不同速度列车混行背景下，通过对铁路现有设计方案评价分析，从系统工程角度提出高铁生命周期内实施选项设计评价的体系框架。

在安全评价方面，随着我国低碳交通与可持续发展理念的推广，基于全生命周期的评价理论开始逐步运用在铁路碳排放和安全系数测算上。如付延冰等[5]将高铁生命周期分为基础设施建造、运营和回收3个阶段，并以京沪高铁为例，分析了高速铁路在建造、运营2个阶段碳排放的特点；冯旭杰等[6]从高铁全生命周期的视角，基于机械做功构建运营、维护2个阶段的高速列车安全指数测算模型，并据此分析高速铁路在投入运营后的各项安全评价指标特征。

然而，以上研究虽然弥补了我国在铁路全生命周期评价理论方面的空白，但没有考虑不同阶段下，铁路项目各参与主体对不同评价目标的偏好特性，无法对多个铁路方案在全生命周期视角下进行综合比选与分析。故为了量化多主体参与条件下的铁路项目全生命周期评价特点，首先将铁路项目分为设计、施工与运营等3个阶段，按照各阶段主体参与率大小选出参与主体，根据主体偏好特性得到它们在经济效益、环境影响与安全性能等3个子目标上的偏好程度，再结合现有铁路项目全生命周期的指标体系，构建多目标指标评价模型并设计拉格朗日乘子算法求解，最后以贵广铁路案例验证模型的有效性与实用性。

1 全生命周期阶段划分

对于不同类型的铁路项目，一般需经历：调查、规划、评估，确定项目投资；勘察、选址、设计、施工；设备安装、试车；竣工验收，交付使用；日常运营，运营养护等阶段。由于各阶段间的相互影响，为保证项目在整个生命周期的健康发展，将铁路项目的全生命周期分为3个阶段：决策设计阶段、施工建设阶段、运营维护阶段[7]。各阶段主要任务如表1：

表1 铁路生命周期各阶段主要任务Table 1 Primary mission at each stage in railway life cycle

2 各阶段主体偏好分析

2.1 参与主体分类

在阶段划分的基础上，铁路项目的主体可分为3类：市场性主体、社会性主体和政府性主体[7]。其中，政府性主体占据主导地位，它将铁路项目具体授权给市场性主体，由市场性主体进行设计、施工和运营等活动，并将服务提供给社会性主体，最终由社会性主体通过实践，将评价反馈给政府性主体，作为铁路项目评价的指标和依据。三大主体的关系[7]如图1：

图1 铁路建设项目三大主体Fig. 1 Three subjects in railway building project

2.2 各阶段参与主体

各阶段参与主体，是指能影响项目的决策、活动或结果的个人、群体及组织。考虑到铁路建设项目各方利益者的关系，笔者认为通过建立合同或者非合同关系，主动或者被动参与铁路建设项目的个人、群体及组织均包含在铁路建设项目三大主体内。

结合《铁道部关于发布铁路基本建设管理程序及职责分工的通知》(铁计函[2014]393号)文件，笔者按决策设计、施工建设、运营维护3个阶段分别选取铁路建设项目的参与主体。各参与方及其参与率按(铁计函[2014]393号)文件所设数值而定，如表2：

表2 铁路建设项目各阶段参与方的参与率Table 2 Participation rate of participants at each stage in railwaybuilding project %

注：主体参与率指在铁路项目全生命周期内，各主体对项目的影响或贡献度大小。如参与率为80%，指该主体在这一阶段参与了铁路项目80%的具体事项，或该主体在这一阶段的80%时间内对铁路项目进度产生影响。

考虑到各阶段涉及的政府部门，设计单位和社会团体等参与方较多，各个环节联系较为紧密。故在项目运作的实际过程中，往往是参与度最高的主体具有较高的话语权和决定权。基于此，以“集体决策、分工合作”的原则，假定各阶段参与率前三位的主体对该阶段的铁路项目运作与具体实施具有最大程度的决定权，并将直接影响项目各单位的分工和各环节的具体实施情况，而其余参与方起着监督，配合等作用，与参与主体共同完成相应的工作或任务。故根据参与率大小，每个阶段的参与主体(参与率)如下：

1)决策设计阶段

铁路总公司(97.03%)、政府部门(96.11%)和勘察设计单位(89.63%)。

2)施工建设阶段

建设单位(94.07%)、施工单位(92.96%)和监理单位(89.41%)。

3)运营维护阶段

铁路总公司(97.03%)、监理单位(89.44%)和政府部门(88.52%)。

通过阶段划分与参与率的比较，可得到铁路项目全生命周期内各阶段的参与主体并为指标体系构建提供基础。

3 铁路多目标指标评价体系构建

3.1 指标的选取

铁路项目常用评价目标有经济效应、环境影响与安全性能等，由于铁路项目的统计指标非常繁杂，难以在全生命周期内获得统一口径的数据，故往往采用Vague集约简备选指标集合[8]，获得与经济效应、环境影响和安全性能3个评价子目标最相近的指标。而笔者选用《中国铁道百科全书(运输与经济)》的评价指标集如下[9]：

表3 评价指标集Table 3 Evaluation index set

3.2 指标体系构建

根据评价指标集合构建指标体系，一般做法是采用层次分析法，根据评价结果对单个指标的设置和整个指标体系的结构进行调整，反复数次，以获得一个较为满意的指标体系。针对铁路项目系统规模大、子系统多、系统内部各种关系复杂等特点，应依据不同阶段下不同目标的指标进行多层次、多目标的结构设计。笔者基于既有研究，将指标体系分为：目标层、类目标层、类别层和指标层等4个层次，并采用下图2层次结构表示[6]。

图2 指标体系示意Fig. 2 Schematic diagram of index system

4 多主体偏好综合评价

通过以上分析，对铁路建设方案的综合评价工作分两步完成：某阶段主体偏好信息的确定；全生命周期指标的评价。

4.1 基于阶段特性的多主体偏好分析

设多目标评价问题有f1(x)，f2(x)，…，fm(x)等m个目标，对目标fk(x)分别给以权重系数λk(k=1,2,...,m)，构建一个新的目标函数如下：

(1)

计算所有方案的F(x)值，从中找出最大值的方案，即为最优方案。在多目标评价问题中，由于各个指标的量纲不同，应先将指标值变换成效用值或无量纲值，再用线性加权和法计算新的目标函数值并进行比较。

4.1.1 模型变量整理

归纳铁路全生命周期里各阶段特性的3(m=3)个子目标：“经济效益(G1)”、“环境影响(G2)”、“安全性能(G3)”。设g1,g2,…,g11,g12分别表示速度目标值、线路长度、…、事故发生率、安全建设费等12个约简指标变量。若某目标铁路项目有3(i=3)个备选方案(分别记为方案A1，方案A2，方案A3)，则指标变量汇总如表4：

表4 建设项目方案评价指标参数说明Table 4 Instructions of evaluation parameters in building schemes

上述变量aij(i=1,2,3j=1,2,…12)构成决策矩阵，评价准则函数如式(2)：

(2)

式中：E(Ai)为第i个方案的最后评价值；λk为第k个子目标的权重，k=1,2,3。

4.1.2 指标数值预处理

考虑到各个指标值的数值大小与量纲不同，因此对它们按相同量纲的列进行归一化处理[9]，令：

(3)

将所有指标值消除量纲并统一到区间[0，1]内。

4.1.3 评价模型构建

记第Gk1个子目标对第Gk2个子目标相对重要性的估计值为Gk1k2(k1,k2=1,2,3)，并近似地认为该值等于这两个目标的权重值之比λk1/λk2。当决策者对Gk1k2(k1,k2=1,2,3)的估计一致时，Gk1k2=λk1/λk2，否则Gk1k2≈λk1/λk2，即Gk1k2λk2-λk1≠0。故选择1组权重λ=(λ1,λ2,λ3)，使得：

(4)

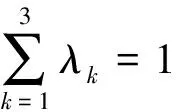
4.1.4 评价模型求解[10]

引入拉格朗日乘子α将带有约束条件的极值问题转化为无约束极值问题，构建拉格朗日目标函数如式(5)：

(5)

首先对拉格朗日目标函数Z′求λk2(k2=1,2,3)的偏导：

(6)

利用不完全归纳法，当k1=1,2,...,n时，分别有：

k1=1时

(7)

k1=2时

(8)

k1=3时

3-2G33λ3+α=0

(9)

……

k1=n时

(10)

令k1=1,2,3(即n=3时)，通过对式(10)在此条件下的恒等变形与合并同类项。

(11)

令λ=(λ1,λ2,λ3)，m=(-α,-α,-α)。将式(11)按k1=1,2,3以矩阵行形式展开：

(12)

得出Hλ=m。引入单位列向量e=(1,1,1)T，推导测出Hλ*=me，进而

λ*=-αH-1e

(13)

(14)

因此得到优化问题最优解：

(15)

由于最优解λ*与第Gk1个子目标对第Gk2个子目标的相对重要性估计值Gk1k2(k1,k2=1,2,3)有关，而Gk1k2值由铁路建设方案的阶段主体(参与主体)决定。因此，设在铁路全生命周期的特定阶段下，3个参与主体(X1、X2、X3)在该阶段的主要参与率分别为：τ1,τ2,τ3(其中τi∈[0.8,1.0])，各主体采用“专家打分法”对建设方案的3个子目标：“经济效益”、“环境影响”、“安全性能”在特定阶段下的相对重要度进行评估，其相关矩阵分别为：G1,G2,G3。故最终的相对重要性估计值Gk1k2，可由式(16)计算确定：

(16)

将最优解带入评价准则函数

E(Ai)=λ*×b

(17)

E*(Ai)[1×12]=(λ(1),λ(2),λ(3),λ(4),λ(5),λ(6)⋮λ(1),λ(2),λ(3)⋮λ(1),λ(2),λ(3))×b

(18)

其中，各子目标的指标偏好率相互间以“⋮”符号分割表示。

4.2 全生命周期的铁路多主体偏好综合评价

对于铁路建设方案Ai，其全生命周期有3个阶段，需分别采用基于阶段特性的多主体偏好分析方法进行评价与汇总。

4.2.1 决策设计阶段

该阶段参与主体为：铁路总公司(97.03%)、政府部门(96.11%)和勘察设计单位(89.63%)。它们对子目标：“安全性能”、“环境影响”、“经济效益”的相对重要度矩阵取值存在偏好差异，故分别设为：(G1)′,(G2)′,(G3)′，而矩阵内的具体取值按“专家打分法”给出(数值均为四舍五入)。

计算最终的相对重要度估计值Gk1k2′：

(19)

由式(19)可得：

4.2.2 施工建设阶段

该阶段参与主体为：建设单位(94.07%)、施工单位(92.96%)和监理单位(89.41%)。各个主对子目标相对重要度矩阵(G1)″,(G2)″,(G3)″，具体取值为

计算最终的相对重要度估计值Gk1k2″，可得：

4.2.3 运营维护阶段

该阶段参与主体为：建设单位(97.03%)、施工单位(89.44%)和监理单位(88.52%)。各个主对子目标相对重要度矩阵(G1)‴,(G2)‴,(G3)‴,具体取值为

计算最终的相对重要度估计值Gk1k2‴，可得：

将得到的Gk1k2′、Gk1k2″、Gk1k2‴带入式(16)、式(15)计算出各阶段的(E*(Ai)[1×12])′、(E*(Ai)[1×12])″、(E*(Ai)[1×12])″，并按各阶段在铁路建设项目全生命周期内的比重0.5,0.25,0.05汇总得到方案Ai的指标偏好评价值。

E*(Ai)=50%×E′(Ai)+25%×E″(Ai)+25%×E‴(Ai)

(20)

在这里，E*(Ai)为1×12的行向量，内部数值可定量反应方案Ai在全生命周期的指标偏好大小。最后分别计算不同建设方案的E*(Ai)值，并选取其中的最大值：

(21)

作为最终的决策选取方案。

5 案例分析

以贵广铁路为案例，采用《新建铁路—贵阳至广州线总体设计方案》、《新建铁路—贵阳至广州线调整初步设计》以及《新建铁路—贵阳至广州线调整可行性研究报告》数据，对多主体影响下的铁路综合评价方法进行分析与验证。

通过资料分析与整理得到贵广线3个研究报告书，并分别简记为方案1、方案2、方案3。其相应评价指标汇总如表5：

表5 3个方案评价指标量化汇总Table 5 Summary of quantitative evaluation index of 3 schemes

将各项指标利用式(3)进行归一化处理，方案Ai评价准则层E(Ai)的计算如式(22)：

(22)

故模型待解未知参数为H-1,由式(9)计算可得；其内部的Gk1k2由各阶段主体偏好下的相对重要度矩阵Gk1k2′、Gk1k2″、Gk1k2‴分别予以计算。因此得到全生命周期各阶段的矩阵(H)′,(H)″,(H)‴及其逆矩阵如下。

1)决策设计阶段

2)施工建设阶段

3)运营维护阶段

带入方程组式(22)，计算12个指标在各阶段下的权重数值E′(Ai)、E″(Ai)、E‴(Ai)，并由式(20)

得出衡量3个方案全生命周期指标权重的评价准则层E*(Ai)如表6。

从表6看出，3个方案各自的指标偏重特点是鲜明的。方案1对速度目标值(0.442)、平均周转量(0.509)、平均上座率(0.493)等指标比较偏重；方案2对线路长度(0.616)、坡度系数(0.864)等指标比较偏重；而方案3偏重坡度系数(0.864)指标，对其他指标考虑较少。因此，选择方案1兼顾因素较多，相比方案2与方案3,能够使铁路线路经过的城市区域范围内达到对经济、环境和安全等目标的效应最大化。故笔者所选方案与实际建设启用方案一致，验证了指标体系及评价方法的有效性。

6 结 语

基于阶段特性构建铁路全生命周期指标体系，再融合主体偏好信息定量评价各指标的偏好大小。通过贵广铁路的多方案设计思路，验证了笔者所提方法的有效性。研究结果旨在为不同铁路参与方在自身偏好特性下进行规划、设计方案比选提供决策参考。

由于笔者是在经济、环境和安全3个目标出发构建评价指标，但铁路建设项目在设计、施工等环节还有土建工程等重要技术指标。因此筛选选线与工程设计指标是下阶段研究方向。

参考文献(References)：

[1] MOHAN A V, K N KRISHNASWAMY, Marketing programs across different phases of the product life cycle: an exploratory study in the Indian machine building sector[J].AsiaPacificJournalofMarketingandLogistics, 2006,18(4): 354-373.

[2] XIE Xiaoling, SIMON M. Simulation for product life cycle management [J].JournalofManufacturingTechnologyManagement, 2006, 17(4): 486-495.

[3] HASSSAN Y, GIBREEL G. Evaluations of highway consistency and safety: practical application [J].JournalofTransportationEngineering, 2000, 23(3): 244-260.

[4] SONG Tong, ZHOU Yan. Automaticsynthesis of fault tree for control systems based on system analysis [J].SystemsEngineeringTheoryMethodologyApplications, 2005, 14(6): 515-516.

[5] 付延冰,刘恒斌,张素芬. 高速铁路生命周期碳排放计算方法[J]. 中国铁道科学,2013,34(5)：140-144.

FU Yanbing, LIU Hengbing, ZHANG Sufang. Calculation method for carbon dioxide emission in the life cycle of high-speed railway [J].ChinaRailwayScience, 2013,34(5): 140-144.

[6] 冯旭杰,孙全欣,冯佳,等. 高速铁路既有停战方案优化模型. [J] 交通运输工程学报,2013,13(1):84-90.

FENG Xujie, SUN Quanxin, FENG Jia, et al. Optimization model of existing stop schedule for high-speed railway [J].JournalofTrafficandTransportationEngineering, 2013,13(1): 84-90.

[7] American Project ManagementInstitute.AGuidetotheProjectManagementBodyofKnowledge[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2013.

[8] MAEDA H, MURAKAMI S. The use of a fuzzy decision-making method in a large-scale computer system choice problem [J].FuzzySetsandSystems, 1993, 54(3): 235-249.

[9] 沈庆衍. 中国铁道百科全书(运输与经济)[M]. 北京：中国铁道出版社,2001：433-440.

SHEN Qingyan.EncyclopediaofChinaRailwaysTransportation&Economy

[M]. Beijing: Publishing of China Railways, 2001: 433-440.

[10] 杨长根. 基于多目标决策模型的铁路主要技术标准选择 [J]. 铁道工程学报,2013,30(8):62-67.

YANG Changgen. Selection of main technical standards for railway based on the mufti-objective decision-making model [J].JournalofRailwayEngineeringSociety, 2013,30(8): 62-67.