考虑地层岩性及地质构造的区域边坡岩体完整程度预测

易 武，王 鸣，于冬升，韩晶晶，张金团

(1. 三峡大学 土木与建筑学院，湖北 宜昌 443002;2. 湖北长江三峡滑坡国家野外科学观测研究站，湖北 宜昌 443002; 3. 贺州学院 建筑工程学院，广西 贺州 542899)

0 引 言

岩质边坡失稳具有爆发突然，危害巨大的特点，预测预报极其困难，并且岩质层状边坡在山区公路边坡以及三峡库区非常普遍，因此对于岩质边坡的稳定性问题需要重点关注[1-3]。岩体完整程度与岩质边坡的稳定性密切相关，而边坡不同的稳定性现状对于在该区域开展工程项目或进行规划建设时显得尤为重要，因此开展岩质边坡完整程度预测是关乎岩质边坡稳定性的一项重要基础性研究。

传统的岩体完整程度的确定主要是通过波速计算或裂隙统计得到的，工作量较大，而对于区域面积较大的范围，由于受到条件及资源约束无法完全通过实地调查得到，因此，笔者利用GIS的空间分析功能，在实地调查采集到的有限基础数据的条件下，建立数学模型,并考虑到地层岩性以及地质构造对岩体完整程度的影响,对研究范围内的其他区域岩体完整程度进行预测，该方法可以大大降低统计工作量。

1 区域概况

1.1 地理位置

研究范围位于三峡库区秭归县沙镇溪镇，地处长江干流右岸，支流青干河以及锣鼓洞河左岸(见图1)。

图1 研究区域地理位置Fig. 1 Geographical location of the studied area

1.2 研究范围及地质特征

通过实地调查得知，研究区域内覆盖层较薄，主要表现为岩质边坡的的范围可以划分为一、二、三区(见图2)，并且均表现为顺向坡。一区主要出露侏罗系中下统聂家山组基岩，岩性主要为厚及巨厚层砂岩、薄层和厚层泥岩，坡度15°～35°，二区主要出露侏罗系中下统聂家山组基岩，岩性主要为厚层砂岩、薄层和厚层泥岩，坡度20°～35°，三区主要出露侏罗系下统香溪组和三叠系中统巴东组基岩，岩性主要为厚及巨厚层砂岩、薄层和厚层泥岩，坡度20°～40°[2-6]。

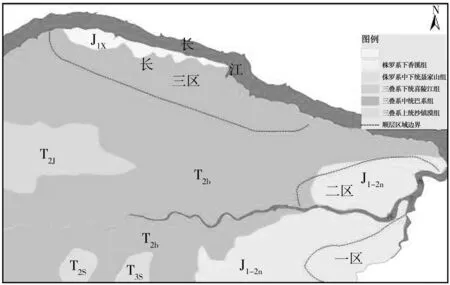
图2 岩质边坡空间分布Fig. 2 Spatial distribution of rock slope

2 影响因子处理

2.1 地层岩性因子

通常在确定岩体完整程度时，主要与岩体结构面发育程度有关，而最直观的体现就是岩体节理裂隙的发育状况。显然，不同的地层岩性，其成分、结构、胶结物及胶结类型等均有差异，而且，风化节理、构造节理等次生节理的形成往往由于岩体成分结构构造等呈现差异化，故在研究岩体完整程度时，有必要考虑地层岩性。

由图2可见, 顺层边坡一区位于锣鼓洞河左岸，二区位于青干河左岸，主要分布侏罗系中下统聂家山组岩层，岩性主要为中到强风化的泥岩与粉砂岩互层，三区位于长江右岸，主要分布三叠系中统巴东组岩层，三区上游局部出露侏罗系下统香溪组，岩性主要为泥岩、砂岩夹泥灰岩地层。此类地层最大的特点是岩层软硬相间。岩体稳定性与岩石抗压性能和抗剪能力密切相关，为此，参考谷德振教授“岩体质量系数”概念，建立评价区域岩体坚固性能的“岩体坚固系数”，即

Z=M·f·S

式中：M为地层单层平均厚度(绝对值，下同)；f为岩层软弱结构面或软弱夹层的平均摩擦系数；S=Rb/100，Rb为岩层平均饱和抗压强度。

上述岩体坚固系数是建立在大量实验数据和数理统计基础之上，地层单元岩体坚固系数值越大，岩体抗压以及抗剪强度越高，岩体稳定性也就越好，因此以岩体坚固系数大小作为地层岩性影响因子的输入值分配的依据，按照不利于边坡稳定性的岩性赋值越大原则，在ArcGIS中将其赋予对应时代的岩性栅格像元值，见图3。

图3 研究区域岩性分类值Fig. 3 Lithological classification of the studied area

2.2 地质构造因子

区域内地质构造复杂，鉴于其对边坡稳定性影响方式，将以距离大小用来衡量地质构造对边坡稳定性的影响程度，在ArcGIS系统中，采用欧式距离进行制图计算，欧式距离给出的是每个像元到最近源(在这里指地质构造要素)的距离，对于像素单元，通过用xmax于ymax作为三角形两直角边来计算斜边距离方法，确定其与最近源的欧氏距离，如图4。

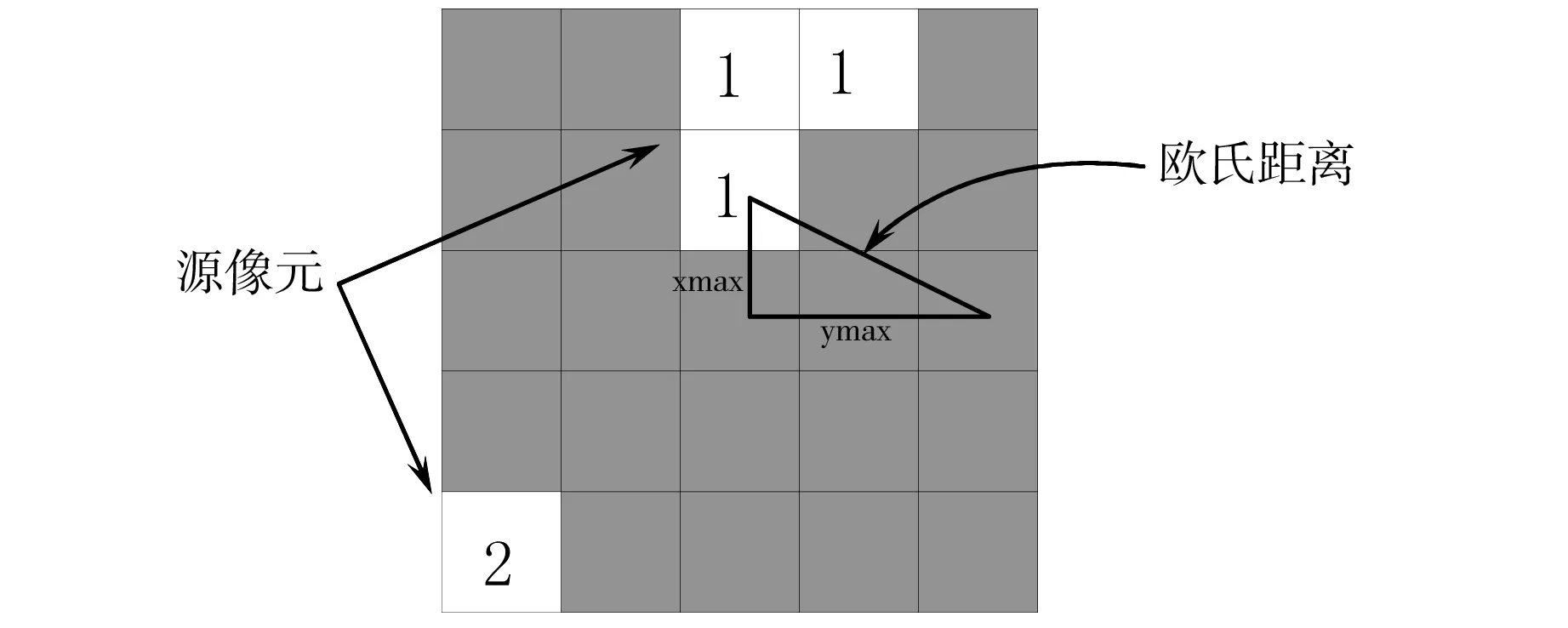
图4 栅格像元欧式距离计算示意Fig. 4 Schematic of the Euclidean distance calculation of grid pixels

同样，为便于计算显示，将所有像元至地质构造要素的欧氏距离分为15个等级，具体分类间隔采用自然断点法分类，自然断点法主要是基于数据本身的固有自然分组，对分类间隔进行识别，并对所有相似值进行归类，使得各类分组的差异性最大，图5为最终的地质构造分类。

图5 地质构造欧式距离分类Fig. 5 Euclidean distance classfication of geological structure

3 区域岩体完整程度预测

3.1 岩体完整程度定义

参考GB 50021—2001《岩土工程勘察规范》(2009年版)中关于岩体完整程度等级的定性划分标准，对研究范围内岩质边坡的岩体完整程度等级进行划分[1]，具体分类标准见表1。

表1 岩体完整程度等级定性划分标准Table 1 Standard for qualitative classification of rock mass integritydegree

(续表1)

完整程度结构面发育程度组数/组平均间距/m主要结构面的结合程度相应结构类型较破碎2～31.0～0.4结合差裂隙块状或中厚层≥30.4～0.2结合好或一般中薄层状结构破碎≥30.4～0.2结合差裂隙块状≤0.2结合一般或差碎裂状结构

3.2 加权叠加预测模型

经实地调查，根据表1规则，可以确定每个调查点的岩体完整程度值，此时为离散值栅格，为了便于计算分析，采用克里金插值求解得到整个研究区域的连续的岩体完整程度值栅格，作为基础栅格，并标准化，最后加权叠加基础栅格和标准化地层岩性以及地质构造影响因子这3个栅格图层，得到最终的研究区域岩体完整程度预测[7-10]。

对区域内岩质边坡的岩体完整程度预测主要是基于区域栅格单元进行，采用加权叠加方法进行计算。假设Xi,j为第i个因子的区域栅格里第j个像元值，其中i=(1,2,…,m)，j=(1,2,…,n)，又设yt为第t个区域栅格单元的叠加像元值，t=(1,2,…,n)，其计算公式如下：

yt=λ1·X1,t+λ2·X2,t+…+λi·Xi,t

(1)

式中：λi为第i个因子的权重值；Xi,j为标准化之后的栅格像元值。

对于权重值，采用相关系数法进行确定。利用MATLAB软件提取研究区域因子栅格单元值，存储为因子矩阵，并以基础栅格作为参考因子，假设参考因子变量为X0(t)，则Xi(t)为第i个变量因子的区域栅格里第t个像元值,i=(1,2,…,m)，t=(1,2,…,n)，则影响因子两两相关系数γ计算公式为

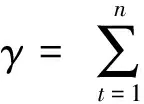
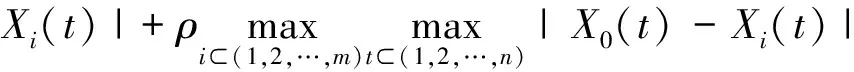
(2)

式中：ρ为分辨率系数，一般可取0.5。

设基础栅格系数为1，并将与另外两个影响因子计算得到的相关系数进行归一，MATLAB求解得到的因子最终相关系数见表2。

表2 因子相关系数Table 2 Factor correlative coefficients

3.3 模型预测

受条件所限，在开展野外实地调查测量时仅仅只能沿调查线路可以到达的范围进行，并选取236个调查点，总共测量到437条节理裂隙的相关数据，具体的节理裂隙调查点分布见图6。

图6 裂隙调查点分布Fig. 6 Distribution of fissure survey points

依据调查点测量得到的系列数据，可以根据表1的分类标准，确定每个调查点的岩体完整程度等级，由于篇幅所限，这里只列举10个调查点的调查统计数据，如表3。

表3 部分调查点调查统计Table 3 Survey and statistics of some survey points

为了得到整个研究范围的边坡岩体完整程度，这里利用已知的236个基础调查点，采用克里金插值(Kriging)计算得到基于调查点的整个范围岩体完整程度状况，即基础栅格。具体计算结果经标准化之后见图7。

图7 基础栅格Fig. 7 Basic grid

现在采用上述加权叠加预测模型，将地层岩性以及地质构造因子进行加权叠加得到图8的预测结果，为了了解预测结果的准确性，将该研究范围内已知滑坡点叠加至图8。由图8可知，整个研究范围内边坡岩体的完整程度从完整到破碎均有分布，并且从计算结果可知，长江干流边坡岩体完整程度要明显差于支流边坡，深色区域如木鱼包滑坡范围，台子湾东滑坡区段，红石溪滑坡区段等，表明该部分边坡岩体完整程度非常差，呈破碎状。

图8 加权叠加对照Fig. 8 Weighted superposition chart

而且从图8可以发现，预测结果为深色的区域，比如木鱼包滑坡范围，台子湾东滑坡区段，红石溪滑坡区段等，即边坡岩体完整程度较差区域均存在已知滑坡灾害点，特别是大岭电站滑坡已于2014年发生滑动。综上预测结果结合已知滑坡灾害点对照图可知，该预测结果符合实际情况。

4 结 语

笔者基于GIS空间分析软件，通过建立顾及多因子的加权叠加模型，对秭归沙镇溪镇部分区域内的岩质边坡岩体完整程度进行预测，得到了很好的效果，以有限的调查样本数据实现整个区域的岩体完整程度预测，并综合考虑了地层岩性以及地质构造的影响，这为实现区域岩质边坡的稳定性分析提供了更为简便实用的方法。

参考文献(References)：

[1] 易武，孟召平，易庆林. 三峡库区滑坡预测理论与方法[M].北京:科学出版社,2011:55-56.

YI Wu, MENG Zhaoping, YI Qinglin.TheoryandMethodofLandslidePredictioninTheThreeGorgesReservoir[M]. Beijing: Science Press, 2011: 55-56.

[2] 孙玉科，古迅. 赤平极射投影在岩体工程地质力学中的应用[M].北京:科学出版社，1980.

SUN Yuke, GU Xun.TheApplicationofStereographicProjectionintheRockMassEngineeringGeologyinMechanics[M]. Beijing: Science Press, 1980: 58-71.

[3] 李远耀，殷坤龙，程温鸣. R/S分析在滑坡变形趋势预测中的应用[J].岩土工程学报,2010,32(8):1291-1296.

LI Yuanyao, YIN Kunlong, CHEN Wenming. Application of R/S method in forecast of landslide deformation trend[J].ChineseJournalofGeotechnicalEngineering, 2010, 32(8): 1291-1296.

[4] 戴自航,卢才金.边坡失稳机理的力学解释[J]. 岩土工程学报,2006,28(10):1192-1197.

DAI Zihang, LU Caijin. Mechanical explanations on mechanism of slope stability[J].ChineseJournalofGeotechnicalEngineering, 2006, 28(10): 1192-1197.

[5] 戴福初. 从土的应力应变特性探讨滑坡发生机理[J].岩土工程学报,2000,22(1):127-130.

DAI Fuchu. Analysis of landslide initiative mechanism based on stress-strain behavior of soil[J].ChineseJournalofGeotechnicalEngineering, 2000, 22(1): 127-130.

[6] 谭万鹏，郑颖人，王凯. 考虑蠕变特性的滑坡稳定状态分析研究[J]. 岩土工程学报,2010,32(2):5-8.

TAN Wanpeng, ZHENG Yinren, WANG Kai. Stable state of landslides considering creep properties[J].ChineseJournalofGeotechnicalEngineering, 2010, 32(2): 5-8.

[7] 李邵军，KNAPPETT J A，冯夏庭. 库水位升降条件下边坡失稳离心模型试验研究[J]. 岩石力学与工程学报, 2008,27(8)：1586-1593.

LI Shaojun, KNAPPETT J A, FENG Xiating. Centrifugal test on slope instability influenced by rise and fall of reservoir water level[J].ChineseJournalofRockMechanicsandEngineering, 2008, 27(8): 1586-1593.

[8] 贾官伟，詹良通，陈云敏. 水位骤降对边坡稳定性影响的模型试验研究[J]. 岩石力学与工程学报, 2009, 28(9)：1798-1803.

JIA Guanwei, ZHAN Liangtong, CHEN Yunmin. Model test study of slope instability induced by rapid drawdown of water level [J].ChineseJournalofRockMechanicsandEngineering, 2009, 28(9): 1798-1803.

[9] 刘礼领, 殷坤龙. 暴雨型滑坡降水入渗机理分析[J]. 岩土力学, 2008, 29(4): 1061-1066.

LIU Liling, YIN Kunlong. Analysis of rainfall infiltration mechanism of rainstorm landslide[J].RockandSoilMechanics, 2008, 29(4): 1061-1066.

[10] 章广成，唐辉明，胡斌. 非饱和渗流对滑坡稳定性的影响研究[J]. 岩土力学, 2007, 28(5): 965-970.

ZHANG Guangcheng, TANG Huiming, HU Bin. Study of influence of unsaturated seepage on stability of landslide[J].RockandSoilMechanics, 2007, 28(5): 965-970.