基于改进VIKOR法的交通规范编制序列的研究

乔建刚，程 璨

(河北工业大学 土木与交通学院，天津 300401)

交通规范编制序列是指根据交通发展需求确定相关交通规范的编制时间计划，这对统筹安排规范的制定、全面提升交通运输标准化水平、促进交通运输科学发展都具有十分重要的作用。

目前，国内外对规范编制方面的研究较少。石彦琴等[1]用层次结构和三维坐标表示了农业工程建设标准体系的构架；孙智等[2]基于标准维度序列优先规则，提出了构建工程建设标准体系的新方法；舒印彪等[3]根据中国现行电力系统安全稳定相关标准的不足，指出未来发展方向。这些研究者从不同方提出各行业规范的规划建设，但都未从编制序列方面进行研究。目前，规范制定序列的确定多采用专家座谈方式，受参与人员主观因素的影响较大，因此采用一种科学的决策方法对规范编制序列进行系统安排，对提高规范制定的专业性和效率具有实际意义。

1 交通规范编制序列算法

1.1 多属性决策VIKOR法

多属性决策的具体方法较多，侧重方面也有所区别。国内外学者主要针对各种方法改进和不同领域应用进行了研究[4-8]。考虑到通过问卷形式参与决策的专家数量较多，且由于各专家对待规范编制序列问题的侧重点不尽相同，所以可把参与调查的专家作为一个属性集，以此为基础进行多属性决策，以确定交通规范编制序列。这样一来模糊分析、法灰色聚类等确定各属性权重方法在此便不再适用。而TOPSIS法和VIKOR法根据不同规范相对理想解和非理想解距离对方案的优劣进行排序方法可适用于此。

多准则妥协解排序(VIKOR法)是南斯拉夫学者S.OPRICOVIC等[9]提出的一种基于理想点解的折衷排序法。其基本思想是在确定正理想解和负理想解基础上，根据各方案评价值与理想方案接近程度对方案进行优选排序。

从综合角度来说，VIKOR法采用了Lpj-mertic发展而来的聚合函数，如式(1)：

(1)

式中：1≤p≤∞；j=1,2,…,J表示备选方案个数；测度Lp为方案aj到理想解的距离。

1.2 二元语义

由于规范编制序列问题的复杂性和不确定性，以及决策主体的主观因素影响，各专家往往不能给出一个具体的编制年份，而是使用自然语言(如：急需、不需要等)的形式来表达自己意愿。近年来不确定语言多属性决策问题已引起了许多学者重视。杨山亮等[10]和A.SHEMSHADI等[11]分别提出了采用直觉和梯形模糊数扩展VIKOR法的多属性群决策模型，但模糊数计算方法繁琐且与语言变量对应关系存在主观性；刘培德等[12]和李磊等[13]分别针对指标权重未知多属性决策问题和铁路突发事件应急预案评估问题，将语言评估值转化为二元语义参与计算，这较好解决了语言转换过程的失真问题。综上所述，专家们将自然语言转化为二元语义信息，并应用于VIKOR法中。

二元语义是西班牙学者F.HERRERA等[14]于2000年首次提出的。其语言评价信息与二元语义之间转化、比较和距离关系可利用以下定义和规则：

定义1：设S为预先设定好的由奇数个元素l构成的有序自然语言评价集；β是一个位于[0,l-1]中的数。则与β对应的二元语义可由式(2)得到：

Δ：[0，l-1]→S×[-0.5,0.5]

Δ(β)=(si,ai)

(2)

式中：i=round(β)，round为四舍五入取整算子；ai=β-i，a∈[-0.5, 0.5]。

则存在逆函数Δ-1，将二元语义转换成相应的数值，如式(3)：

Δ-1：S×[-0.5,0.5]→[0，l-1]

Δ-1(si,ai)=i+ai=β

(3)

定义2：假设(si,ai)、(sk,ak)为两个二元语义，关于二元语义之间的比较有如下规定：

若i>k，则(si,ai)>(sk,ak)；

定义3：设(sδ,aδ)、(sγ,aγ)为两个二元语义，则其距离如式(4)：

d(sδ,aδ),(sγ,aγ)=Δ-1(sδ,aδ)-Δ-1(sγ,aγ)

(4)

1.3 二元语义改进VIKOR算法

根据以上论述，用二元语义可改进VIKOR法，使其适用于交通规范的编制序列确定。通过二元语义的定义1，可解决专家评价的自然语言信息转化问题，构建专家评价矩阵，用于VIKOR法中；通过二元语义的定义2，可确定理想解和负理想解；通过二元语义的定义3，可分别计算VIKOR法中最大群体效应值S、个体遗憾最小值R和所有备选方案的折衷值Q，并根据所得结果进行排序，最后根据Q值得变化及VIKOR中的折衷方案确定交通规范编制序列。

2 二元语义改进VIKOR法的应用

天津地区濒临渤海，其中天津港是我国北方的第一大港，具有港口货运量大、堆积物品多、重型车量多、降雨量大、对周围环境影响大等特点；天津市内河流较多，货运和客运量较大，跨河桥梁数量多、种类差别大；加之天津地区具有多雨多雾、空气中盐分含量大、多分布有软土地基等地区特征。针对这些特点，笔者对22项待编标准进行了调研分析。

待编制的22项规范用ai表示，对水运行业不同专业方向的42位同等水平专家进行调研，构成属性集B={bj}，j=1,2,…,42，且专家决策权重相同。

2.1 第1步

专家按“急需1年”～“急需5年”、“一般”、“暂缓”和“不需要”等标准对各规范编制时序进行评价，根据式(2)将专家语言评价值转化为二元语义形式，构建二元语义评价矩阵，如式(5)：

(5)

式中：基本语言评价集S=(s0=“不需要”，s1=“暂缓”，s2=“一般”，s3=“急需”，s4=“十分急需”)；其中，s3对应“急需3～5年”，s4对应“急需1～2年”。

2.2 第2步

在确定正理想解和负理想解时，其标准是一致的，故正负理想解相应就是在确定语言评价集情况下最高级和最低级评价所对应的二元语义。

利用定义2确定正负理想解，如式(6)：

(6)

2.3 第3步

根据式(3)、(4)，计算所有规范最大群体效应值S和个体遗憾最小值R，如式(7)：

(7)

2.4 第4步

计算所有备选方案的折衷值Qi，如式(8)：

(8)

就规范编制序列问题而言，群体效应应占主要位置，但考虑到个体可能会根据实际经验得出不同结果，也要适当减小个体遗憾。因此笔者计算了υ=0.7和υ=0.8这两种情况，结果如式(9)、(10)：

(9)

(10)

2.5 第5步

确定排列顺序，按Ri值从小到大排序，方案排在前面的比后面的需要更早制定标准。并将排序后的Ri值绘制成散点图。分别就υ=0.7和υ=0.8所得Q值进行排序，得表1；排序后的Qi值绘制成图1。

表1 Q值排序(υ=0.7、υ=0.8)Table 1 Q values sorting table (υ=0.7,υ=0.8)

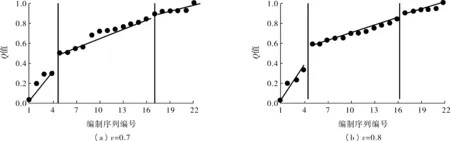
图1 Qi值排序散点图Fig. 1 Qi value sorting scatter plot

2.6 第6步

根据Q值得变化及VIKOR折衷方案确定交通规范的编制序列规划。

张志刚[15]结合城市交通发展战略规划和轻重缓急原则，提出规范编制的时间分为近期、中期和长期的规划原则。笔者引用此方法确定了交通规范编制序列。

由表1和图1可发现：当υ=0.7和υ=0.8时，序列顺序除2与4对调外，其他完全相同，总体变化规律也基本一致。笔者分析不同υ值差异：当υ=0.7时，在序列8、9之间出现了一个较大跳跃，其对应规范为18和20，专家评价统计如图2。

图2 规范18和规范20专家评价结果Fig. 2 Expert evaluation results of standard 18 and 20

可发现：这两者差距不大，规范20出现较大跳跃是因为相较规范18存在两个“不需要”评价。说明υ=0.7与υ=0.8相比较，其过度考虑个体遗憾最小情况，出现了一定偏差，因此取υ=0.8情况下的排序确定水运规范编制序列是合适的。

根据Ri变化规律：序列1～4以相似斜率远离理想解，序列4与序列5之间出现一个较大跳跃，考虑VIKOR法折衷解确定方法，因此把序列1～4所对应的规范归入近期计划；同理，把序列5～16所对应规范归入中期计划；17～22所对应规范归入长期计划。最终得到了天津水运规范编制序列，如表3。

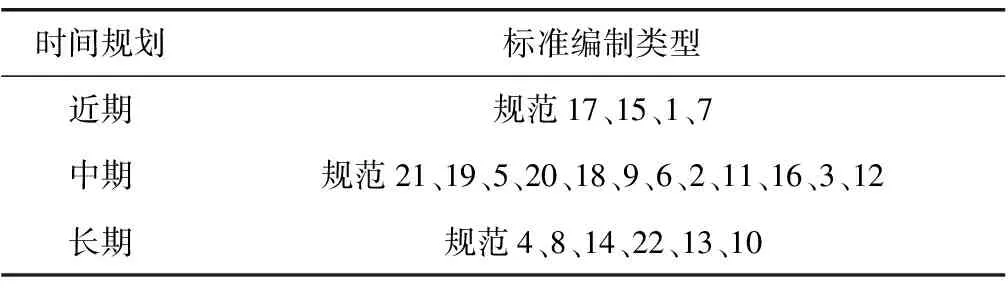
表3 天津水运规范编制序列Table 3 Compilation sequence of water transportation in Tianjin

3 TOPSIS法比较分析

为验证模型可行性和实用性，笔者采用二元语义改进TOPSIS法(逼近理想解)对文中决策矩阵进行分析，并与VIKOR算法结果进行比较。在TOPSIS法中，利用各规范标准与理想解和非理想解相对贴近度c确定规范序列，c值越大则说明时序越早，见图3。

图3 c值排序散点图Fig. 3 c value sorting scatter plot

根据c值斜率变化，可看出序列1～4斜率相近，将其对应规范列入近期计划，之后斜率变化不大，但序列16和17的c值差相对较大，故以其为分界点分别将其对应规范列入中期和长期计划。对比基于二元语义的TOPSIS法和VIKOR法所得结果完全一致，说明改进VIKOR法完全可行。这两种方法不同编制时间计划间斜率及差值比较见图4。

由图4可看出：相比TOPSIS法，VIKOR法不同序列间斜率变化率更加明显，提高率达到了70.8%；其差值更大，提高率达86.4%和76.0%。VIKOR法能更显著区分不同序列间的区别，对规划制定者而言辨识度更高，而且VIKOR法中关于折衷解定义，使规范编制时间规划更加科学。同时VIKOR法在时序制定过程中可根据评估情况和专家水平不同，设置不同的决策机制系数υ，考虑群体效益和个别遗憾相互妥协，得到更为合理的编制序列。

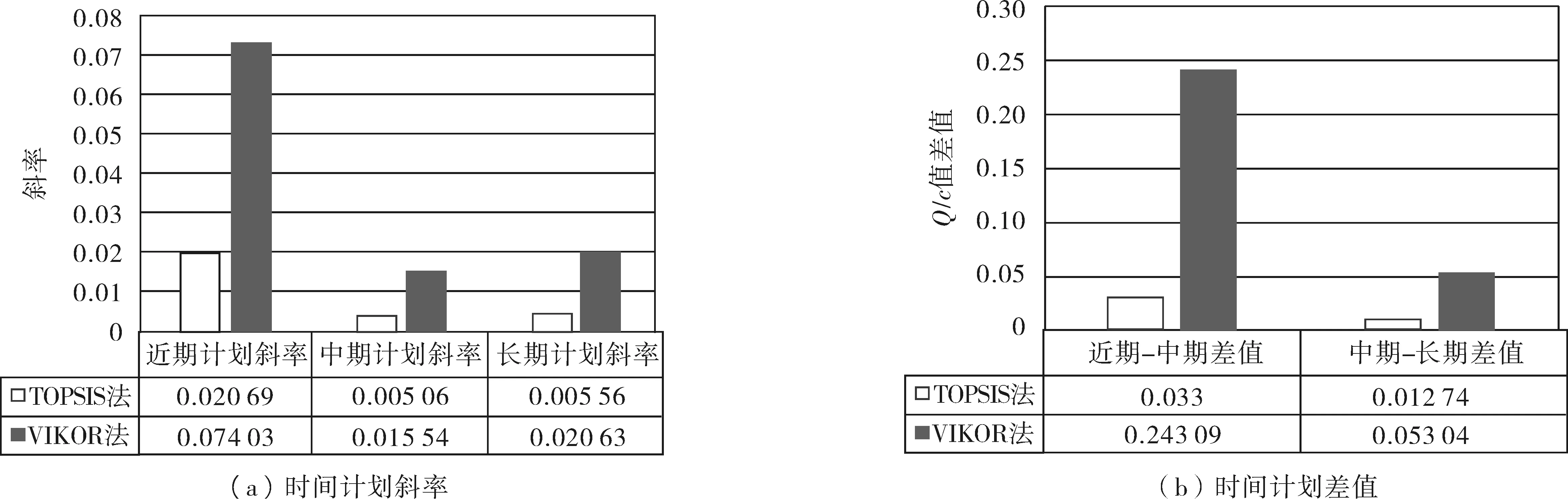
图4 两种方法对比Fig. 4 Comparison of two methods

4 结 语

笔者提出了采用二元语义改进VIKOR法确定交通规范编制序列的思路。用二元语义将专家语言评价进行转化，使其可用于计算，之后根据各规范距离理想解和非理想解的距离，结合VIKOR折衷解确定方法和规范编制时间计划，得到交通规范编制序列。

以天津地区水运规范编制序列为例，确定了规范编制序列，并使用TOPSIS法进行验证和对比分析，验证了该方法准确性和实用性，为各地区交通标准编制序列的确定提供了一种新方法。

参考文献(References)：

[1] 石彦琴，赵跃龙，李笑光，等.中国农业工程建设标准体系构架研究[J].农业工程学报，2012，28(5)：1-5.

SHI Yanqin, ZHAO Yuelong, LI Xiaoguang, et al. Infrastructure of standard system for agricultural engineering construction in China [J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2012, 28(5): 1-5.

[2] 孙智，张守健.工程建设标准体系的复杂性研究[J].土木工程学报，2012，45(增刊2)：277-283.

SUN Zhi, ZHANG Shoujian. Research on the complexity of construction standard system [J].ChinaCivilEngineeringJournal, 2012, 45 (Sup2): 277-283.

[3] 舒印彪，汤涌，孙华东.电力系统安全稳定标准研究[J].中国机电工程学报，2013，33(25)：1-8.

SHU Yinbiao, TANG Yong, SUN Huadong. Research on power system security and stability standards [J].ProceedingsoftheCSEE, 2013, 33 (25): 1-8.

[4] HWANG C L, YOON K.MultipleAttributeDecisionMaking[M]. New York: Springer-Verlag, 1981.

[5] 梵治平，陈发动，张晓.基于累计前景理论的混合型多属性决策方法[J].系统工程学报，2012，27(3)：295-301.

FAN Zhiping, CHEN Fadong, ZHANG Xiao. Method for hybridmultiple attribute decision making based on cumulative prospect theory [J].JournalofSystemsEngineering, 2012, 27(3): 295-301.

[6] 杨玉中，张强，吴立云.基于熵权的TOPSIS供应商选择方法[J].北京理工大学学报，2006，26(1)：31-35.

YANG Yuzhong, ZHANG Qiang, WU Liyun. Technique for order preference by similarity to ideal solution based on entropy weight for supplier selection [J].TransactionsofBeijingInstituteofTechnology, 2006, 26(1): 31-35.

[7] 袁宇，关涛，闫相斌，等.基于混合VIKOR方法的供应商选择决策模型[J].控制与决策，2014，29(3)：551-560.

YUAN Yu, GUAN Tao, YAN Xiangbin, et al. Based on hybrid VIKOR method decision making model for supplier selection [J].ControlandDecision, 2014, 29(3): 551-560.

[8] 罗圆，姚令侃，魏永幸.铁路选线方案比选指标权重确定及灵敏度分析[J].重庆交通大学学报(自然科学版)，2015，34(6)：73-78.

LUO Yuan, YAO Lingkan, WEI Yongxing. Weight determination and sensitivity analysis of scheme comparison index in railway location [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34 (6): 73-78.

[9] OPRICOVIC S, TZENG G H. Extended VIKOR method in comparison with outranking methods [J].EuropeanJournalofOperationalResearch, 2007, 178(2): 514-529.

[10] 杨山亮，王鹏，李革，等.基于直觉模糊VIKOR方法的装备优选群决策模型[J].系统仿真学报，2015，27(9)：2169-2175.

YANG Shanliang, WANG Peng, LI Ge, et al. Group decision making model for weapon selection using extended VIKOR method under intuitionistic fuzzy environment[J].JournalofSystemSimulation, 2015, 27(9): 2169-2175.

[11] SHEMSHADI A, SHIRAZI H, TOREIHI M, et al. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting [J].ExpertSystemswithApplications, 2011, 38(10): 12160- 12167.

[12] 刘培德，关忠良.一种基于二元语义的混合型多属性决策方法[J].控制与决策，2009，24(7)：1074-1077.

LIU Peide, GUAN Zhongliang. Hybrid multiple attribute decision making method based on 2-tuple [J].ControlandDecision, 2009, 24(7): 1074-1077.

[13] 李磊，王富章.基于改进多准则妥协解排序(VIKOR)法的铁路应急预案评估研究[J].中国安全科学学报，2012，22(8)：29-35.

LI Lei, WANG Fuzhang. Research on evaluation of railway emergency plan based on improved VIKOR method [J].ChinaSafetyScienceJournal, 2012, 22(8): 29-35.

[14] HERRERA F, MARTINEZ L. A 2-tuple fuzzy linguistic representation model for computing with words [J].IEEETransactionsonFuzzySystems, 2001, 8(6): 746-752.

[15] 张志刚.基于聚类分析方法的地方标准规划序列研究[J].交通标准化，2014，42(12)：169-172.

ZHANG Zhigang. Planning order of local standards based on clustering analysis method [J].TransportationStandardization, 2014, 42(12): 169-172.