中小学数学思想方法的有效衔接—以特殊与一般思想在小学几何教学中的运用为例
2018-05-31广东省广州市天河区棠下小学赵加永
广东省广州市天河区棠下小学 赵加永
《义务教育数学课程标准》指出:“学生要理解和掌握基本的数学知识与技能,还要体会和运用数学思想和方法,获得基本的数学活动经验.”新的课程标准突破了只重视“双基”的局限性,初次把数学思想作为义务教育阶段,尤其是小学数学教育的基本目标,强调数学思想的重要性.笔者一直潜心研究数学思想在小学数学中的应用,本文以特殊与一般思在小学几何教学中运用为例进行介绍.
一、特殊与一般思想简介
数学思想是指人们对数学理论和内容的本质的认识,是数学科学发生、发展的根本.数学思想蕴涵在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括而成的数学观点.特殊与一般思想是数学思想中一个非常重要的思想方法,它可以从特殊问题开始,经过分析、比较、归纳、抽象、概括,提炼出一般规律,然后去解决实际问题.而对于难以求解的一般问题,也可以把一般问题特殊化,发现解决问题的途径,进而解决一般问题.
二、特殊与一般思想在小学几何教学中的运用
特殊与一般思想在初中几何学习中占据非常重要的地位,但是它在小学几何教学中运用却不多.为了做好中小学几何教学的衔接,在小学教学中遇到可以利用特殊与一般思想解决问题时,教师一定要抓住弥足珍贵的机会.
(一)挖掘特殊与一般思想在小学几何教材编写中的渗透
1.人教版教材中探究长方形的面积运用了由特殊到一般的思想.教材中通过任取几个1平方厘米的正方形,拼成不同的长方形,数出长方形的长、宽、面积,学生对几个特殊长方形的数据分析、比较,归纳出长方形的面积公式.
2.长方体的体积、圆环的面积也是利用由特殊到一般的思想总结出相应的公式.
3.六年级上册新增内容“外方内圆”和“外圆内方”中,求正方形和圆之间部分的面积,六年级下册数学思考,都是对特殊与一般思想的直接运用.
(二)重视特殊与一般思想在课堂教学中的渗透
1.把特殊与一般思想写进教学目标
制定精准的教学目标是上好一堂课的基础,教学过程的设计要围绕着教学目标开展.因此,教学上述内容时,要把特殊与一般思想写进教学目标,要把它与知识技能目标一样重视,只有这样才能把思想方法的运用落到实处.
2.在知识的形成过程中体现特殊与一般思想方法
小学数学学习的一大特点是很多法则、性质、公式、定律等,是通过实验、观察、猜想、类比、归纳等非演绎推理方法获得的.学生经历和体验了这些知识的形成过程,有利于理解所学知识及其背后的原理,有利于提炼概括数学思想方法,提高学生的思维水平和思想方法方面的数学素养.
例如:人教版六年级数学下册100页《4.数学思考》

第一要让学生操作体验图形变化的过程.学生可以从2个点开始连线,逐渐增加点数,边连线边思考每增加1个点,线段增加的条数和线段总条数的变化,然后填写表格,写出算式.
第二要寻找规律,用明确的语言符号和图式表示变化的规律.每增加1个点,线段增加的条线就是点数减1,而线段总条数就是从1依次连加到点数减1的自然数之和.因此,我们知道了点数,就可以从1开始,依次加到点数减1的自然数,所得的和就是总线段数.这样就从几个特殊的情况,归纳概括出一般情况总线段数与点数之间的关系.
第三用字母简洁扼要的表示一般规律.n个点连成线段的条数:1+2+3+4+…+(n−2)+(n−1)或n×(n−1)÷2.
最后是运用阶段,利用归纳出的一般规律解决问题,可以轻松求出12个点、20个点,甚至是100个、1000个点能连成线段的条数.
学生经历操作、观察、归纳、提炼解决问题的过程,亲身体验用特殊与一般思想解决问题,使他们学会了一种解决问题的方法,为日后的学习打下一个扎实的基础.
(三)练习中要灵活运用特殊与一般思想解决数学问题
1.利用特殊化的思想解决填空题、选择题或判断题中的疑难问题例如:如图,长方形的面积为35平方厘米,左边直角三角形的面积为5平方厘米,右上角直角三角形的面积为7平方厘米,那么中间三角形(阴影部分)的面积是____平方厘米.
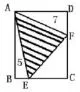
图1
分析因为长方形的面积为35平方厘米,不妨假设AB=5厘米,AD=7厘米,因为S△ABE=5平方厘米,所以BE是2厘米,EC是5厘米,同理:DF是2厘米,CF是3厘米,S△ECF是7.5平方厘米,阴影部分面积:35−(7+5+7.5)=15.5(平方厘米)
本题如果利用常规的解题方法,小学生无从下手,总感觉缺少条件,没有几个学生能正确求解,但是根据已知条件,利用特殊化的方法赋予长方形长、宽具体数值,问题可以得到轻松解决.
2.利用特殊到一般思想解题
例如:求一个十六边形的内角和是多少度?
分析对于学生来说,十六边形画起来都很困难,求它的内角和就更困难了.所以,学生先画最简单的三角形、四边形、五边形等特殊的多边形,研究内角和与边数之间的关系,归纳总结出多边形的内角和公式,然后再用公式求出十六边形的内角和.
三、结语
德国数学家希尔伯特曾说过:“问题是数学的心脏,方法是数学的行为,思想是数学的灵魂.”拥有了灵魂,学生就掌握数学学习的真谛,数学素养就能不断提升,就能为中学的学习打下扎实的基础.
[1]教育部基础教育课程教材专家工作委员会组织编写:《义务教育数学课程标准(2011年版)》,北京师范大学出版集团,2012年2月出版.
[2]吴增生.数学思想方法及其教学策略初探[J].数学教育学报,2014,23(03):11-15.
[3]王永春.小学数学与数学思想方法.华东师范大学出版社,2017年,第10页.
[4]http://www.aoshu.com/e/20120910/504d581526fc5.shtml
