“一个折叠问题中两个角大小比较”的再思考*

江苏省盱眙中学(211700) 董培仁

问题在图1的 △ABC中,边AB=25、AC=40,高AD=24,沿高AD将△ABC折成如图2的几何体,试考虑∠BAC与∠BDC大小关系.

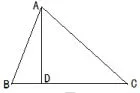
图1

一、学生的思考

学生给出的结论大都是∠BAC＜∠BDC.

图2

不少学生是这样看的:在图2中,因为AD⊥BD,AD⊥CD,所以AD⊥平面BCD,∠BDC是∠BAC正投射到平面BCD得到的,显然应该有∠BAC＜∠BDC.有学生将图2中△ABC“平放”到平面BCD上 (如图3),连接AD并延长交BC于E.由于三角形的一个外角大于不相邻的一个内角,则∠BDE＞∠BAE,∠EDC＞∠EAC,所以∠BDC＞∠BAC.

图3

二、教学的处理

为了纠正学生错误,我们在讲解时用“极端化”方法进行了处理,即:当折的幅度很小(接近图1情形)时,∠BDC接近180°,显然∠BAC＜∠BDC;而当折的幅度很大(接近B在DC上的图4情形)时,∠BDC接近0°,显然∠BAC＞∠BDC.因此,∠BAC与∠BDC谁大谁小是不确定的.

图4

上面的处理,并没有给出两个角大小关系转换具体情形,虽学生不得不接受结论,但不能理解两个角大小转换的原因.

为让学生理解,我们通过计算两个角的余弦进行处理.

在图2中,Rt△ABD的斜边AB=25,一直角边AD=24,则另一直角边Rt△ACD的斜边AC=40,一直角边AD=24,则另一直角边DC=32.设BC=d,由于DC−BD＜BC＜DC+BD,则BC=d∈(25,39).由余弦定理:由得222d2=205950,即则当时,cos∠BAC＞cos∠BDC,即∠BAC＜∠BDC;当时,cos∠BAC=cos∠BDC,即∠BAC=∠BDC;当时,cos∠BAC＜cos∠BDC,即∠BAC＞∠BDC.因此,∠BAC与∠BDC的大小是不确定的.

三、问题的再思考

我们给出了“极端化”和求余弦值的两种解法后,学生不得不承认∠BAC与∠BDC的大小是不确定的这个结论.但一些喜欢思考的同学多次与我探讨这个问题,始终不明白直观体验到那么明显的关系怎么就是错误的,原因到底在哪里?

事实上,学生对图的形状与相应数据没有对应好.为让学生的“弯子”能绕过来,我们参照学生的“平放”法,在学校的江苏省“数字化高中课程基地”里进行了试验.

在图5中作DH⊥BC,垂足为H,连接AH.由于AD⊥平面BCD,则AD⊥BC,又DH⊥BC,AD∩DH=D,所以BC⊥平面ADH,故BC⊥AH.再将△ABC“平放”到平面BCD上(如图6),则AH⊥BC且D在AH上.我们将图6中AB、AC、BD、DC、AE(过D、H)做成骨架,且D、H在骨架AE上都可以滑动,移动B、C点(始终有AE⊥BC).由于BC∈(25,39),我们就考察B与C两点距离d在(25,39)范围内变化时,∠BAC与∠BDC的大小关系.

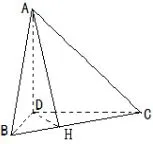
图5

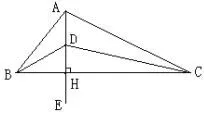
图6

d在(25,39)范围内变化时,会出现三种情况:H在BC之间、H与B重合、H在CB的延长线上.

图7

由条件及前面的计算已知AB=25,AD=24,BD=7,AC=40,AD=24,DC=32,d=BC∈(25,39).

若H在BC之间 (如图7(1))时,∠DBH是锐角,则BD2+BC2＞DC2得所以d＜39.此时∠BDH是△ABD中∠BDA的外角,则∠BDH＞∠BAD,同理∠CDH＞∠CAD,则显然有∠BAC＜∠BDC.

若H与B重合 (如图7(2))时,显然有∠BAC＜∠BDC.

若H在CB的延长线上(如图7(3))时,易知25＜d＜情况比较复杂,下面进行具体分析.由于H在BC之间、H与B重合两种情形都有∠BAC＜∠BDC,因此两个角大小转换应该在“H在CB的延长线上”这种情形中发生.

学生得出错误结论的原因:一是只想到了“H在BC之间”这一种情形;二是虽然有的想到了三种情况,但认为“H在CB的延长线上”这种情形下仍只有∠BAC＜∠BDC.

对于错误一的纠正,要引导学生考虑∠DBC＞90°、∠DBC=90°的情况,再进一步进行处理.

对于错误二的纠正,考虑到学生对“H在CB的延长线上情形中,图的形状与相应数据没有对应好,我们先引导学生从图形的模型变化中进行体验,再用数的形式进行推导与计算.

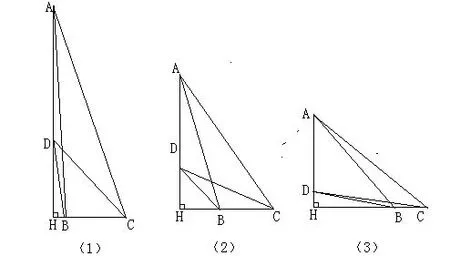
图8

我们在图6的骨架中,移动B、C点(D、H在骨架AE上滑动,始终有AE⊥BC),让BC逐渐变小,学生就会体验到两个角的大小就会出现三种情形变化:∠BAC＜∠BDC(如图8(1)),∠BAC=∠BDC(如图8(2)),∠BAC＞∠BDC(如图8(3)).

为了让学生理解形的变化与数量的变化保持一致,先看下面的一个问题:

如图9,∠MON=90°,点A、B在射线OM上,其中OA=a,OB=b(b＞a＞0),点C是在射线ON上的动点,当∠BCA取得最大值时,求OC的长.

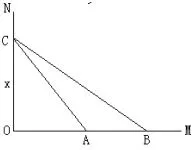
图9

设OC=x,则可 得 tan∠BCA= tan(∠OCB−∠OCA) =即 tan∠BCA=我们知道:上是增函数,在上是减函数;y=tanx在上增函数.因此容易知道:时,x越大,tan∠BCA越大,所以∠BCA越大;时,x越大,tan∠BCA越小,所以∠BCA反而越小.故当时,∠BCA取得最大值.

因此,“H在CB的延长线上”情形中(如图7(3)),虽然A在D的上方,并不总有∠BAC＜∠BDC,而是有对应图8中的三种情形.

事实上,由于25＜d＜39,结合上面余弦定理计算的结果,数形对应如下(如图10):

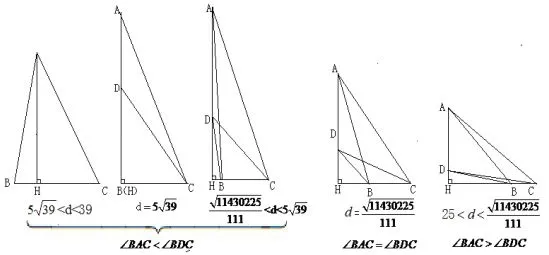
图10

当25时,∠BAC＞∠BDC;当d=时,∠BAC=∠BDC;当时,∠BAC＜∠BDC.

在后来的交流中,那些提出疑问的学生接受了上面对问题的处理.这也让我们体会到:在问题处理中,数形之间不能切合时,若只从一个角度进行思考,虽然能得出解答,但并没有让学生真正理解,难以达到应有的教学效果.因此,不能为了解决问题,只用“数解形”或用“形解数”,而是要让两者在真正地结合.这就要求我们在教学中,让“做”与“算”建立协作体,对于学生不理解的“算”,要通过技术手段“做”出来让学生看,同样对于学生不理解的“做”时,要通过“算”出来帮助理解,让两者全方位、多角度、深层次交互作用,达到真正地切合,才能让教学效果最优化.