数学命题:让“变”生长在教材母题上—一道七年级期末测试题的命制与启示

广东省珠海市金鼎中学(519085) 吕尧华

笔者有幸参与了2017年珠海市七年级第二学期期末数学试题的整个命制过程且担任命题组长.全卷共20道小题,下面笔者结合试卷中的第18题的命制过程,谈谈对“教材母题”改造的具体做法和命题启示.

一、命题的过程

第18题命题起始制定双向细目表时对这道题目的定位是:(1)有关“第五章相交线与平行线”的几何综合题;(2)既要控制难度又要考察学生解决几何问题的能力.

基于以上定位,确定命制此题的切入点:先选择合适的“母题”,经过一番思考后,确定以下这道题目作为命制第18题的“母题”.

教材母题:(课本第37页第13题)

(1)如图1,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,DE//BA,DF//CA.求证:∠FDE=∠A.

(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.求证:AC//BD.

图1

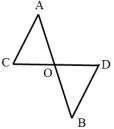
图2

第18题的雏形如图3,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,AG与DE的延长线交于点G,∠1=∠3,∠2=∠4,∠5=∠B.

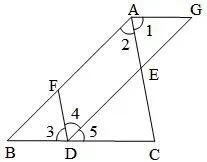
图3

(1)求证:AG//BC;

(2)若AC平分∠BAG,∠C=65°,求∠5的度数.

与命题组的老师商讨后,对第18题的雏形有如下修改意见:

主题干表述冗长,是否可以精简文字?

主题干中已知条件“相等的角的数量”有些多,是否可以去掉一组?

图形中角多、线段多,有些复杂,能否简化图形?

基于以上意见,我对雏形做了如下一番改造:针对“图形中角多、线段多”的问题,我的解决办法是去掉“线段DF”使原有图形中的两个“A”图形变为一个“A”图形以达到简化图形的目的,把∠1与∠2合并成∠BAE,把∠4与∠3合并成∠BDE,以达到减少角的目的,得第18题的第一稿 :

如图4,已知∠1=∠B,∠BAE=∠BDE,AC与DE相交于点F.

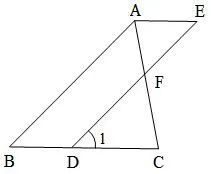
图4

(1)求证:AE//BC;

(2)若AC平分∠BAE,∠C=65°,求∠1的度数.

与命题组的老师再次商讨后,对第18题的第一稿的修改意见:本题的第(2)问与试卷第13题重复考察运用平行线的性质求角度问题,而且问题设置偏简单,没有达到命题起始的定位:既要控制难度又要考察学生解决几何问题的能力.

于是,对第18题的第一稿再做如下改造:我尝试将第(2)问中的已知条件“AC平分∠BAE”变成求证的结论,然后运用“分析法”逆向推理发现已知条件“∠DFC=∠C”,得第18题的第二稿 :

如图5,已 知∠1 =∠B,∠BAE=∠BDE,AC与DE相交于点F.

图5

(1)求证:AE//BC;

(2)若∠DFC=∠C,求证:AC平分∠BAE.

此时第18题“基本”大功告成,为什么说是“基本”,请大家火眼金睛比较“第18题的第二稿”与“第18题的终稿”有什么不同?

第18题的终稿如图6,已知∠1=∠B,∠BAE=∠BDE,AC与DE相交于点F.

图6

(1)求证:AE//BC;

(2)若∠DFC=∠C,求证:AC平分∠BAE.

细心的读者会发现,“图形”有细微的差别,第(2)问中已知“∠DFC=∠C”,所以在画图形时应该准确的体现出来,初一的学生刚刚接触几何证明,不要在题目设计上迷惑学生,给学生解答题目设置障碍.

二、命题的启示

证明题的考核目标在于考查学生的逻辑推理能力.初一学生对几何证明的要求不能过高,因此命题时要注意:

(1)控制证明题试题的难度;

(2)选择学生熟悉的基本的几何图形;(第18题是基本图形“A”字图形与“X”图形的组合图形)

(3)预设多种论证方式.(第18题设计了两种证法,证法1用“同旁内角互补”,结合图形利用“平角”来证AE//BC;证法2用“内错角相等”来证AE//BC.此题的两种证法都运用了数学中的演绎法和分析法.)

如果我们在命题时,让题目之根扎在教材中,再让“变”生长在教材母题上,那么这种寓“变”于教学之中的方法,不但可以以少胜多,而且可以培养学生的探索精神和创新精神,还可以促使学生爱学数学.所以教师在平时教学中要多关注教材中的重点例题、习题,然后由这些题目出发,让“变”生长在教材母题上,由浅入深,由此及彼,让学生越来越对数学感兴趣,越来越爱上数学,变得越来越聪明!