下单翼布局飞机不同整流减阻特性研究

张礼，高正红

(西北工业大学 航空学院，西安 710072)

0 引 言

在气动布局设计中，增升减阻是不断追求的目标，常规布局[1-2]是飞机气动布局[3]形式中最成熟的布局形式，能充分发挥机翼的气动特性。飞机气动阻力中的干扰阻力决定了飞机各部分之间的相互影响，其中最主要的是机翼和机身之间的相互干扰。客机因布置客舱和起落架的需要采用下单翼布局，下单翼是指机翼位于机身下部的纵向相对位置关系。下单翼常规布局飞机的机翼和机身之间较严重的干扰引起附面层堆积，导致气流分离，致使全机阻力增加，因此，有必要通过减弱机翼机身结合处附面层的堆积来减小飞机阻力。Hugo Gagnon等[4]和S. Peign等[5]对减阻进行了探索；M.Drela[6]对升力体机身进行了研究；R.Rudnik等[7]、F.Grand等[8]、Li Chunna等[9]以及Fabien Gand等[10]对机翼机身结合处的流动进行了实验和数值模拟；郭民[11]、Amal Abeysinghe等[12]、John C.Vassberg等[13]、Aakash Narender等[14]对机翼机身结合处的整流装置进行了设计；Xu Shenren等[15]对机翼机身结合处的整流装置进行了优化。但上述研究工作均未对机翼机身结合处安装整流装置对飞机纵横航向特性的影响进行研究。

战斗机对机身与发动机进气道之间因附面层堆积造成分离的解决措施是通过附面层隔道或DSI(Diverterless Supersonic Inlet)进气道来实现，如图1所示。附面层隔道是在进气道和机身间产生气流的通道，通过增加该处气流速度来减弱机身和进气道间的附面层堆积；而DSI进气道则是通过鼓包把进气道和机身间的附面层外推，在气流的作用下该处附面层不易堆积，从而减小飞机阻力。

图1 附面层隔道与DSI鼓包

客机的机翼机身结合处因附面层堆积造成的分离与战斗机进气道与机身间因附面层堆积造成的分离类似。因此，本文借鉴战斗机通过DSI进气道使用鼓包处理附面层的方法，通过对客机机翼机身结合处整流鼓包的外形设计将机翼机身结合处附面层外推，在气流作用下减弱机翼机身结合处的附面层堆积，实现整流减阻；并对几种整流减阻方案进行数值模拟分析，研究整流鼓包对飞机气动特性和纵横航向特性的影响，以期为下单翼常规布局飞机的机翼机身整流减阻提供参考。

1 几何外形和计算网格建模

以所建立的近似于737-800飞机的外形为基础进行整流减阻设计，该飞机巡航状态为0.78Ma，2°迎角，高度11 km。

在建模前对不同整流方案外形进行分析：NM, 没有整流；ZHL1，机翼机身结合处整流，整流包的截面外形外凸(整流包截面形状的上部分和下部分外凸)；ZHL2，机翼机身结合处整流，整流包的截面外形外凸(整流包截面形状的上部分和下部分内凹)；ZHL3，机翼机身结合处加机身腹部整流，整流包的截面外形外凸。三种不同整流方案的比较如表1所示。

为了对比分析的准确性，排除其他因素的影响，三种整流外形均采用相同的上部控制边界、整流前部边界、整流后部边界、展向整流[11]边界。根据文献[11]，前部整流的范围确定为0.15c，后部整流范围为0.3c(c为机身机翼结合处机翼弦长)，为了确保整流罩和机翼的适应度，整流罩的纵向截面应与机翼的剖面形状接近。B样条控制整流罩截面外形，边界线控制边界，通过几何外形参数化造型建立三种不同整流罩下的飞机外形，如图2所示。

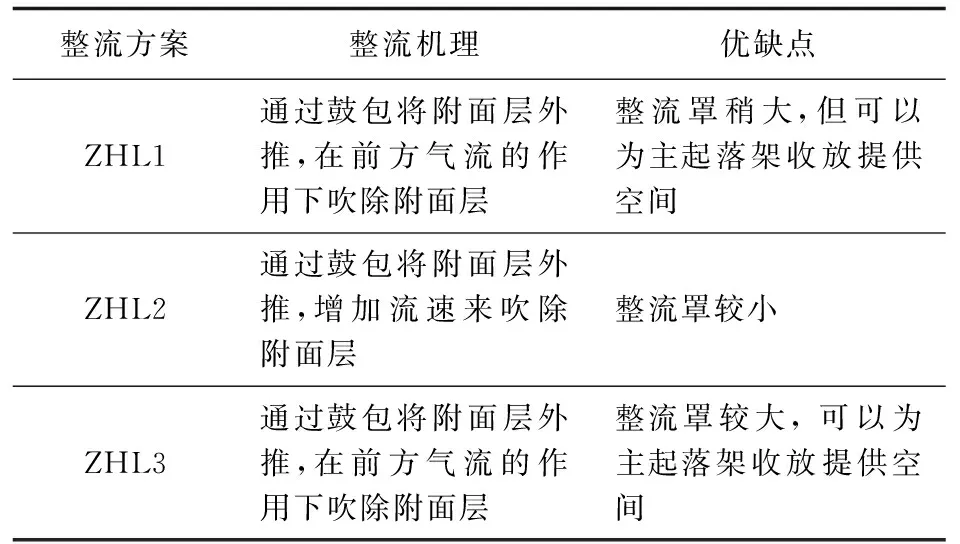
表1 三种整流方式的特点

(a) NM

(b) ZHL1

(c) ZHL2

(d) ZHL3

计算网格采用多块结构网格，为了减小网格对计算结果的影响，NM、ZHL1、ZHL2、ZHL3采用相同的外流场网格分布，物面网格在整流罩曲率变化较大的地方进行了不同程度的加密，其余地方网格相同。三种不同整流罩下的飞机气动网格分布，如图3所示。

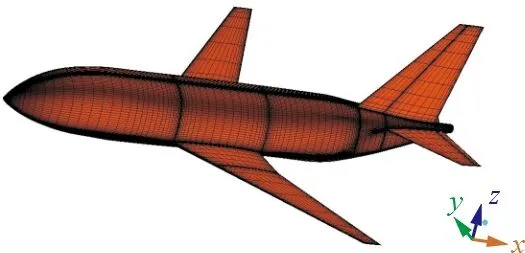
(a) NM

(b) ZHL1

(c) ZHL2

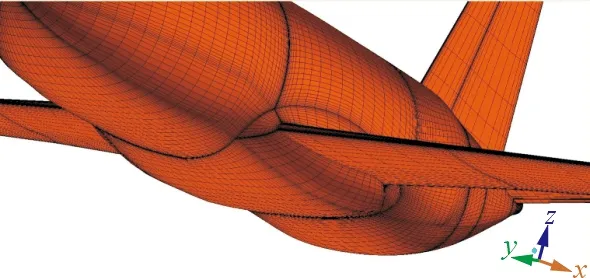
(d) ZHL3

2 计算方法

计算方程采用考虑粘性的N-S方程，直角坐标系下的三维可压非定常N-S方程的守恒积分表达式为

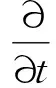
(1)

式中：Q=(ρ,ρu,ρv,ρw,ρe)T，为守恒向量，ρ，(u,v,w)，e分别为密度、直角坐标系的速度分量、单位质量气体的总通量；∂V为某一固定区域的边界；n为边界的外法向量；F为矢通量，可以分解为对流矢通量Fc和粘性矢通量Fv两部分，即F=Fc-Fv。

为了较真实地模拟飞行器流场的复杂流动，需利用考虑粘性的N-S方程求解。受到计算机条件的约束，直接求解N-S方程还只限于少数简单流动的情况。实际工程中通常采用雷诺平均N-S方程(RANS)方法，其主要思路是将满足动力学方程的瞬时运动分解为平均运动和脉动运动两部分，脉动运动对平均运动的贡献通过雷诺应力项来模化，即通过湍流模型来封闭雷诺平均N-S方程，使之可以求解。根据湍流的理论知识、实验数据或直接数值模拟结果，给出雷诺应力的各种经验和半经验的本构关系，从而使湍流的平均雷诺方程封闭。

按照对模型处理的出发点不同，可以将湍流模型分为两大类：一类为雷诺应力模型，另一类为涡粘性封闭模型。受计算条件的限制，雷诺应力模型由于计算量大，应用范围受到限制。在工程中广泛采用涡粘性模型，它仿照粘性的思路提出，假设雷诺应力项为

(2)

当平均速度应变率确定后，六个雷诺应力只需确定一个涡粘性系数vt就可以完全确定，且涡粘性系数各向同性，可以通过附加的湍流项来模化。为了使控制方程封闭，在引入附加湍流项后，需要求解与附加湍流数目相同的附加微分方程。根据要求解的附加微分方程的数目，一般可将湍流模型划分为三类：零方程模型，典型代表为Baldwin-Lomax模型；一方程模型，典型代表为Spalart-Allmaras模型；两方程模型，典型代表为k-ε模型和k-ω模型。此处计算采用k-ε湍流模型。

3 计算结果与分析

整流前部的整流范围为0.15c, 后部整流范围为0.3c，得到的结果如图4所示，可以看出：在-4°～4°迎角范围内，升力系数随迎角线性变化，在α=4°以后出现了非线性；ZHL1、ZHL2、ZHL3相比没有整流外形NM，升力系数有不明显下降,以2°巡航迎角为例，分别下降0.91%、0.6%、3%，ZHL3升力损失最严重。

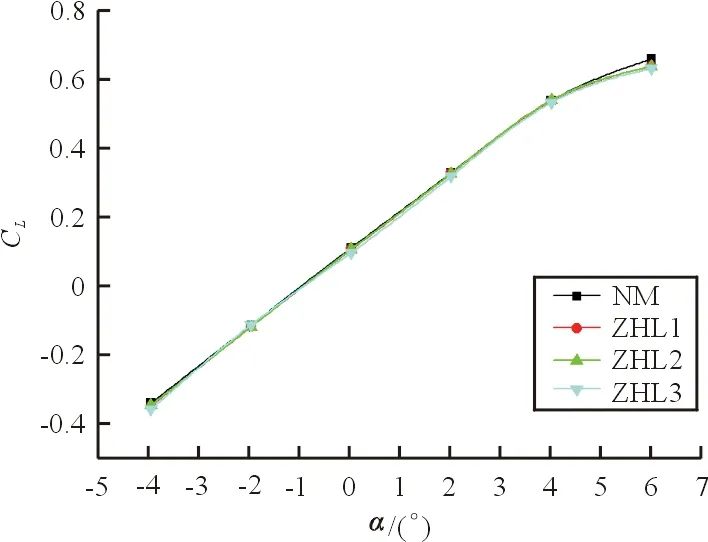
图4 升力系数随迎角的变化曲线

阻力系数随迎角的变化曲线如图5所示，可以看出：ZHL1、ZHL2、ZHL3阻力系数均小于未整流外形NM，达到了整流减阻的目的；α=2°时，相对于未整流外形，三种整流方式阻力系数分别减小5.7%、7.3%、7.4%。

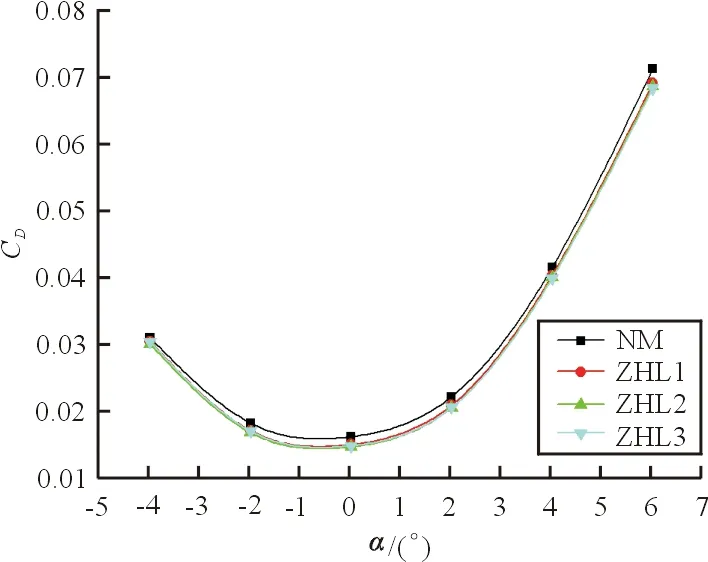
图5 阻力系数随迎角的变化曲线

俯仰力矩系数随迎角的变化曲线如图6所示。

图6 俯仰力矩系数随迎角的变化曲线

从图6可以看出：在-4°～4°迎角范围内，未整流外形(NM)、整流外形(ZHL1、ZHL2、ZHL3)均是纵向静稳定的，且静稳定度相同，在1.5°迎角附近达到力矩为0；在相同迎角下，整流外形相对于未整流外形低头力矩稍大；在4°迎角以后出现了勺形区[13]，且整流外形相对于未整流外形勺形区更显著。

NM、ZHL1、ZHL2、ZHL3均在2°迎角附近达到最大升阻比，故本文将2°迎角作为巡航状态是合适的。升阻比随迎角的变化曲线如图7所示，可以看出：ZHL1、ZHL2、ZHL3相比NM升力系数有少许降低，但阻力系数下降更多，总的来说方案ZHL1、ZHL2、ZHL3升阻比均有不同程度的增益，分别为5.4%、7.4%、4.7%，表明本文的整流减阻方案具有现实可行性。

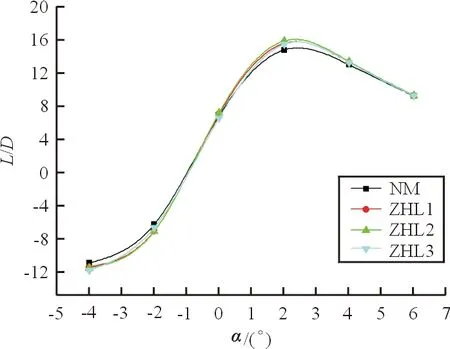
图7 L/D随迎角的变化曲线

飞机的极曲线如图8所示，可以看出：在小于升力系数0.55时，相同升力系数对应的阻力系数均是整流外形小于未整流外形，达到了整流减阻的效果；而在升力系数大于0.55时，由于非线性的影响，效果并不明显。

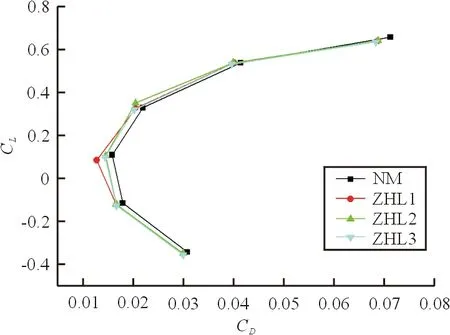
图8 极曲线

滚转力矩系数随迎角的变化曲线如图9所示，可以看出：整流外形相对于未整流外形，有更小的滚转力矩，整流有减小飞机滚转的作用，且整流、未整流外形有相同的滚转力矩随迎角的变化趋势。

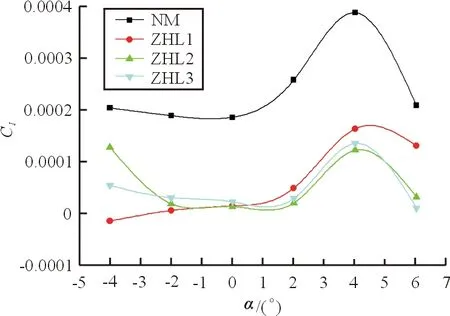
图9 滚转力矩系数随迎角的变化曲线

偏航力矩随迎角的变化曲线如图10所示，可能看出：未整流外形偏航力矩较小，而整流外形有较大的偏航力矩，有增大偏航力矩的趋势，且三种整流外形随迎角变化趋势基本相同，只是ZHL2变化较剧烈。此处未计算偏航力矩随侧滑角的变化, 也没有从航向静稳定度进行分析。

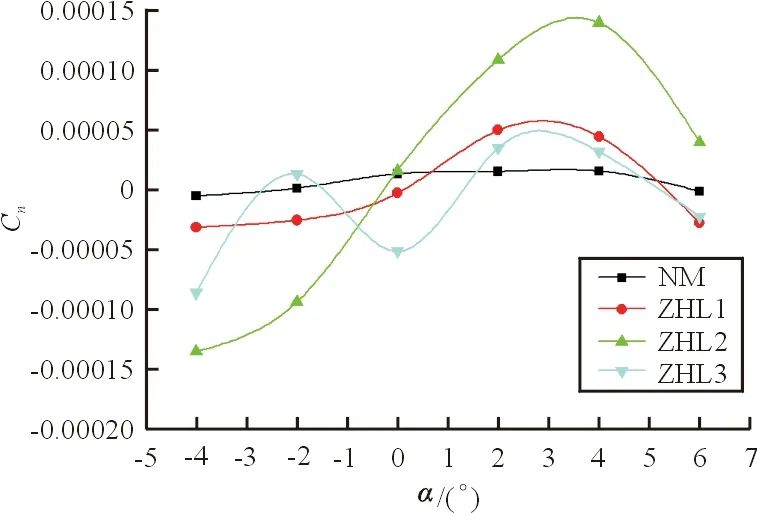
图10 偏航力矩系数随迎角的变化曲线

机翼展向不同剖面的压力分布如图11所示，由于机翼采用弱激波超临界翼型，剖面压力分布具有显著的屋顶状压力分布形态。本文采用的超临界翼型，其上表面后缘向下有一定的弯度，且下表面后缘的内凹并不严重，弥补了传统超临界翼型带来的较大低头力矩，但升力有一定的损失。力矩特性和升阻特性是一对难平衡的矛盾组合体，如何权衡成为应用超临界翼型需考虑的问题。

(a) 机翼16%半展长处剖面的压力分布

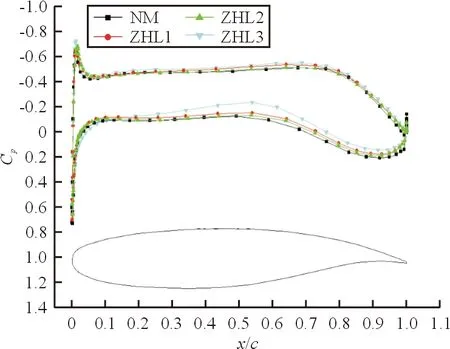
(b) 机翼20%半展长处剖面的压力分布

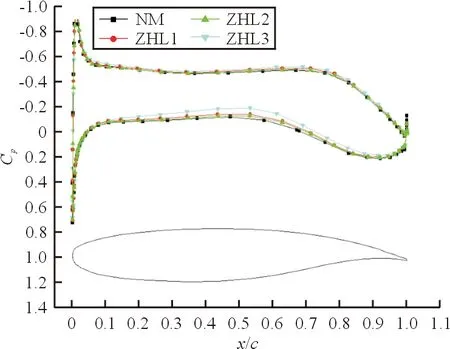
(c) 机翼26%半展长处剖面的压力分布

从图11可以看出：由于机翼机身的相互干扰，内翼剖面前缘的升力损失较大，沿展向远离机翼机身结合处机翼剖面升力逐渐恢复，整流对机翼剖面压力分布的影响沿展向逐渐减小。从图11(a)可以看出：三种整流方案的机翼剖面上表面压力相对于未整流外形有更大的负向压力，对应的流速增大，这对减弱机翼机身结合处附面层堆积有利；而在下表面则有较小的升力(除ZHL3在前缘稍大)，相应下表面流速减小。ZHL3 对机翼剖面的压力分布影响较大，在剖面下表面中部的升力损失较多，即ZHL3相比其他两种整流方案升力损失较多的原因。综上所述，整流对机翼剖面压力分布的影响趋势沿展向逐渐减小。

4 结 论

(1) 本文的整流减阻方案达到了减小阻力的效果，但升力稍有损失，总体来说升阻比有所提高。ZHL2相比其他两种整流方案升力损失最小，减阻效果好，升阻比增益最大，且整流罩最小；ZHL3减阻效果比ZHL1好，但升力损失较多，升阻比相差不大；ZHL3相比其他两种整流方案升力损失较大，主要是由于ZHL3使机翼下表面升力损失较多所致。

(2) 整流对纵向静稳定度没有影响，但使低头力矩有所增大，勺形区加剧；整流能减小滚转力矩，有增大偏航力矩的作用。

(3) 本文针对下单翼布局飞机机翼机身整流的建模计算分析对机翼机身的翼身融合设计具有一定的参考作用。

[1] 李为吉. 飞机总体设计[M]. 西安: 西北工业大学出版社, 2004.

Li Weiji. Aircraft preliminary design[M]. Xi’an: Northwestern Polytechnical University Press, 2004.(in Chinese)

[2] Raymer D P. Aircraft design: a conceptual approach[M]. 5th ed. USA: AIAA Education Series, 2012.

[3] 方宝瑞. 飞机气动布局设计[M]. 北京： 航空工业出版社, 1997.

Fang Baorui. Aircraft aerodynamic layoutdesign[M]. Beijing: Aviation Industry Press, 1997.(in Chinese)

[4] Hugo Gagnon, David W Zingg. Euler-equation-based drag minimization of unconventional aircraft configurations[J]. Journal of Aircraft, 2016, 53(5): 1363-1365.

[5] Peign S, Epstein B Robust. Drag minimization of aerodynamic wings in engineering enviroment[J]. Journal of Aircraft, 2006, 43(3): 1195-1204.

[6] Drela M. Development of the D8 transport configuration[C]. 29th AIAA Applied Aerodynamics Conference. 2010: 2011-3790.

[7] Rudnik R, Sitzmann M. Experimental investigation of the wing-body juncture flow on the DLR-F6 configuration in the ONERA SAMA facility[C]. 27th AIAA Applied Aerodynamics Conference. 2009: 22-25.

[8] Grand F, Monnier J C. Experimental study of the corner flow separation on a simplified junction[J]. AIAA Journal, 2015, 53(10): 2869-2877.

[9] Li Chunna, Ye Zhengyin. Simulation of flow separationat the wing-body junction with different fairings[J]. Journal of Aircraft, 2008, 45(1): 258-266.

[10] Fabien Gand, Vincent Brunet. Experimental and numerical investigation of a wing-body junction flow[J]. AIAA Journal, 2012, 50(12): 2711-2719.

[11] 郭民. 民机翼身整流影响分析与设计研究[J]. 航空计算技术, 2010, 40(3): 10-11.

Guo Min. Impact analysis and design of civil aircraft’fairings[J]. Aeronautical Computing Technique, 2010, 40(3): 10-11.(in Chinese)

[12] Amal Abeysinghe, Julia Whitmire. QTD2(quiet technology demonstrator 2) main landing gear noise reduction fairing design and analysis[C]. 28th AIAA Aeroacoustics conference. 2010: 2007-3456.

[13] John C Vassberg, Anthony J Sclafani, Mark A DeHaan. A wing-body fairing design for the DLR-F6 model: A DPW-Ⅲ case study[C]. 23rd AIAA Applied Aerodynamics Conference. 2005: 4730.

[14] Aakash Narender Singh, Vijay Kumar Govindarajan. Kn-owledge based design methodology for generic aircraft windshield and fairing-a conceptual approach[C]. 51st AIAA Aerospace Sciences meeting. 2013: 0469.

[15] Shenren Xu, Sebastian Timme. Wing-body junction optimization with CAD-based parameterization including a moving intersection[J]. Aerospace Science and Technology, 2017, 79(8): 543-551.