功能梯度材料热传导的统计多尺度边界元分析

黄志强，韩要闯，聂玉峰

(1.西北工业大学 理学院，西安 710072) (2.太原科技大学 应用科学学院，太原 030024)

0 引 言

功能梯度材料[1]是一种在材料的制备过程中通过连续地控制各组分含量的分布使材料宏观特性在空间位置上呈现梯度变化的非均质多相复合材料。由于功能梯度材料的结构和性能呈连续变化，不存在明显的界面，其热力学性能和物理性能也呈梯度变化趋势，满足了结构元件不同部位对材料使用性能的不同要求，进而达到优化结构整体使用性能的目的。面对不断增长的工程应用需求，如何有效表征功能梯度材料的细观结构并建立细观结构与宏观热传导性能之间的定量关系，已成为材料科学与工程领域的重要课题。

研究功能梯度材料宏观等效性能的细观力学解析方法众多，包括Eshelby等效夹杂理论[2]、自洽模型[3]、广义自洽模型[4]、Mori-Tanaka模型[5]、微分法[6]、变分法[7]和n点界[8]等，上述模型均对材料微结构进行了大量简化以减少计算规模，故不能充分反映材料的真实微观结构特征。M.Jabbari等[9]采用直接方法分析了一维和二维稳态功能梯度空心圆筒热传导和热弹性问题；A.Alibeigloo[10]采用傅里叶级数法推导了物性参数沿厚度方向呈指数函数变化的温度场解析解；陶光勇等[11]采用解析法研究了功能梯度材料板在稳态梯度温度场下的热应力分布状况；Shao Z S等[12]利用级数求解法给出了功能梯度圆筒稳态温度场的解析解。采用解析法研究功能梯度材料热传导问题已取得了一些研究成果，但是由于功能梯度材料的非均匀性，利用解析法研究其热传导问题具有很大的局限性。Cao Leilei等[13]采用基本解有限梯度元方法求解了功能梯度材料的稳态热传导问题；王鲁等[14]采用有限元法研究了功能梯度热障涂层在循环状态下的瞬态温度分布。由于功能梯度材料性能的不均匀性，直接使用有限元等传统数值方法时需要非常精细的网格去捕捉功能梯度材料的局部特征，这将导致计算规模的大幅增加、求解困难。因此，建立一种针对功能梯度材料的高效可行的数值算法是十分必要的。

近年来，基于均匀化方法[15]的多尺度分析方法被成功应用于预测不同复合材料结构的物理和力学性能[16-19]。Li Youyun等[16]通过引入随机样本单胞模型，提出了基于有限元方法的统计多尺度分析方法，用于预测颗粒或孔洞随机分布复合材料的热传导性能。考虑到功能梯度材料微结构的随机性，多尺度计算结果呈现很大的发散性，必须进行大量样本的计算，最后给出统计意义上的结果，才能真实地反映随机复合材料的宏观整体导热性能。此外，功能梯度材料中颗粒数量巨大，尺寸较小，且体积分数随着位置变化而变化，结构十分复杂，有限元体网格剖分难度大；同时，为了更好地逼近材料微观结构，需要数量巨大的有限元网格，导致计算规模庞大。与有限元方法不同，边界元方法只需要在功能梯度材料各相材料的界面上进行网格剖分[20]，网格数目少，划分难度小，边界元方法在求解功能梯度材料导热问题上具有显著优势。

本文针对功能梯度材料的稳态热传导问题，描述功能梯度材料微结构的表征方法，建立宏观等效材料参数的多尺度边界元计算模型并给出统计意义下的多尺度算法，并研究颗粒随机分布功能梯度材料的热传导性能。

1 统计多尺度分析模型

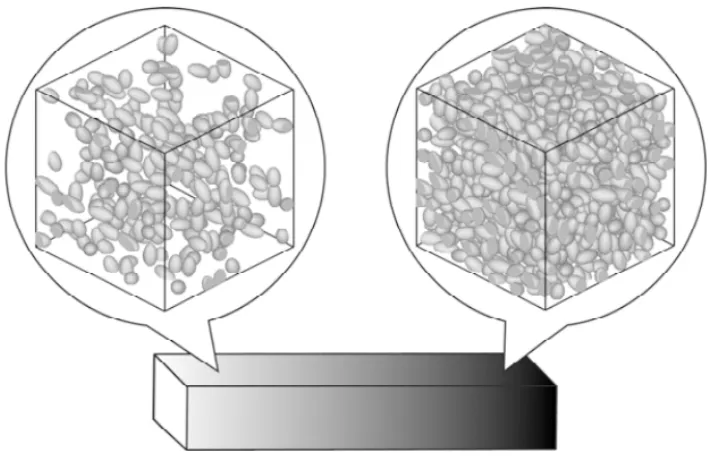
图1 功能梯度材料的细观结构

(1)

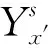
根据上述细观结构表征，考虑随机分布复合材料结构的稳态热传导方程为

(2)

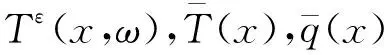
Tε(x,ωs)=T0(x,y,ωx′)+εT1(x,y,ωx′)+

ε2T2(x,y,ωx′)+…

(3)

由于y=x/ε，则存在链式法则：

(4)

将式(3)～式(4)带入式(2)，并整理成ε幂级数的形式，可得：

(5)

通过比较式(5)两端ε不同幂次的系数，根据偏微分方程理论可分别定义T0和T1，则温度场的多尺度渐进展开式可定义为

(6)

(7)

(8)

(9)

利用上述期望的均匀化系数，可以定义功能梯度材料结构的均匀化热传导方程：

(10)

2 统计多尺度边界元算法

由于功能梯度材料中颗粒数量大、满足随机性分布且体积分数随着位置而变化，其微观单胞结构十分复杂，为了有效求解定义在单胞Yx′上的单胞函数，采用有限元方法时需要大量的体网格来逼近单胞结构，计算规模巨大。此外，由于颗粒分布的随机性，必须进行大量样本的计算，最后计算出统计意义上的结果，才能真实地反映随机复合材料的宏观整体性能。因此，采用有限元算法求解期望均匀化系数时计算规模巨大。而边界元方法在求解该问题时只需要在各组分材料的边界上进行网格离散，使得整体网格数量大幅减少，有效地降低了计算规模。假设功能梯度材料中基体和颗粒的热传导性能满足各向同性，则基于边界元方法的统计多尺度算法如下：

(1) 根据给定的概率分布模型P(x)(x∈Ω)，在结构Ω上选择M个点xi(i=1,2,…,M)。

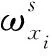
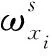
(11)

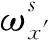
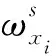
(12)

式中：c(y)为与边界有关的常量(对于光滑边界取值1/2)；v为单位法向量。

进一步对式(12)等号右端的第三项采用径向积分，可得：

(13)

式中：r(p,y)为p点和y之间的距离。

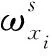
(14)

式中：φi(y)为径向基函数；Φ为径向基函数插值矩阵。

然后采用径向积分方法将区域积分转换为边界积分，即

(15)

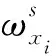
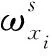
(16)

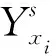
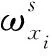
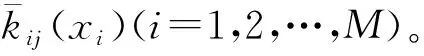
3 算例分析

为了验证统计多尺度边界元方法预测功能梯度材料热传导性能的有效性，取圆球颗粒Al作为增强相颗粒的Al/Al2O3功能梯度材料，Al和Al2O3的热导率分别为211.07和38.27 W/mK，圆球颗粒在基体内均匀随机分布且体积分数随着位置从0～25%线性变化。由于颗粒分布的随机性，数值计算结果会受此影响，即使颗粒的分布模型完全相同，计算结果也会因样本的不同而有所差别。因此，一次样本的计算结果无法完全反映随机复合材料的宏观特性，必须进行大量样本的计算，再最终计算出统计意义上的结果，才能真实反映随机复合材料的宏观整体性能。算例中的计算结果均由随机抽样50次统计所得。

选取不同样本数量时的等效导热系数计算结果如图2所示，可以看出：随着样本数量的增加，计算结果分散性越来越小。

图2 样本数量对等效导热系数的影响

分别使用多尺度有限元和多尺度边界元方法计算等效导热系数的数值结果与实验结果的比较如图3所示，可以看出：在功能梯度材料内部有效热传导系数随着位置的变化呈上升趋势，两种多尺度方法均给出了稳定的预测曲线，与实验数据[22]符合较好。

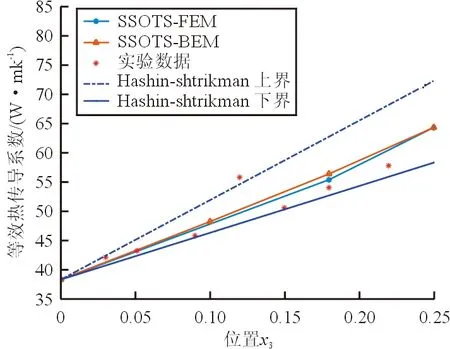
图3 等效导热系数数值结果与实验数据比较

多尺度有限元网格与多尺度边界元网格数目的比较如图4所示，可以看出：边界元网格数目远少于有限元网格数目，采用多尺度边界元算法可以大幅节约计算成本，减少计算量。特别地，针对随机复合材料模拟需要大量取样的特性，多尺度边界元算法节约的计算量是相当可观的。

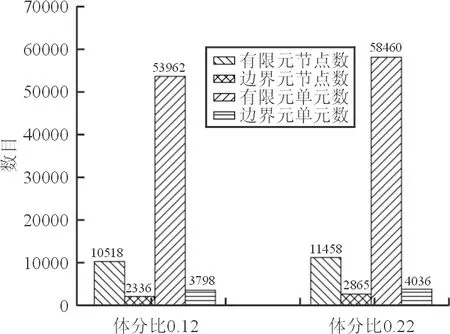
图4 有限元网格与边界元网格数比较

从图3～图4可以看出：统计多尺度边界元方法可以用较少的计算时间得到满意的结果，是一种预测功能梯度材料热传导性能的高效率、高精度的数值方法。

4 结 论

(1) 使用统计多尺度边界元方法预测了颗粒随机分布功能梯度材料的等效导热系数，数值结果与实验结果的比较表明了多尺度边界元模型的正确性和算法的有效性。

(2) 针对具有大量颗粒随机分布且结构和性能在空间位置上呈现梯度变化的功能梯度材料的热传导问题，统计多尺度边界元算法可以用较少的计算时间得到满意的结果，是一种高效率、高精度的数值算法。

[1] 孙兰. 功能材料及应用[M]. 成都: 四川大学出版社, 2015.

Sun Lan. Functional materials and applications[M]. Chengdu: Sichuan University Press, 2015.(in Chinese)

[2] Eshelby J D. The determination of the elastic field of an ellipsoidal inclusion and related problems[J]. Proceedings of the Royal Society, 1957, 2: 267-396.

[3] Budiansky B. On the elastic moduli of some heterogeneous materials[J]. Journal of the Mechanics and Physics of Solids, 1965, 13(4): 223-227.

[4] Kerner E H. The electrical conductivity of composite media[J]. Proceedings of the Physical Society, 1956(69): 802-808.

[5] Mori T, Tanaka K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica, 1973, 21(5): 571-574.

[6] Mclaughlin R. A study of the differential scheme for composite materials[J]. International Journal of Engineering Science, 1977(15): 237-244.

[7] Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials[J]. Journal of the Mechanics and Physics of Solids,1963, 11: 86-93.

[8] Torquato S. Random heterogeneous materials: microstructure and macroscopic properties[M]. New York: Springer, 2002.

[9] Jabbari M, Sorabpour S, Eslami M R. General solution for mechanical and thermal stresses in a functionally graded hollow cylinder due to nonaxisymmetric steady-state loads[J]. Journal of Applied Mechanics, 2003, 70: 111-117.

[10] Alibeigloo A. Exact solution for thermo-elastic response of functionally graded rectangular plates[J]. Composite Structures, 2010, 92(1): 113-121.

[11] 陶光勇, 郑子樵, 刘孙和. W/Cu梯度功能材料板稳态热应力分析[J]. 中国有色金属学报, 2006, 16(4): 694-700.

Tao Guangyong, Zheng Ziqiao, Liu Sunhe. Analysis of steady thermal stress in plate of W/Cu functionally graded material[J]. The Chinese Journal of Nongerrous Metals, 2006, 16(4): 694-700.(in Chinese)

[12] Z S Shao, L F Fan, T J Wang. Analytical solutions of stresses in functionally graded circular hollow cylinder with finite length[J]. Key Engineering Materials, 2004(261/263): 651-656.

[13] Cao Leilei, Wang Hui, Qin Qinghua. Fundamental solution based graded element model for steady-state heat transfer in FGM[J]. Acta Mechanica Solida Sinica, 2012, 25(4): 377-378.

[14] 王鲁, 吕广庶, 王富耻, 等. 功能梯度热障涂层热负荷下的有限元分析[J]. 兵工学报, 1999, 20(1): 51-54.

Wang Lu, Lu Guangshu, Wang Fuchi, et al. Finite element analysis for functionally gradient thermal barrier coatings under thermal loads[J]. Acta Armamentarii, 1999, 20(1): 51-54.(in Chinese)

[15] Bensoussan A, Lions J L, Papanicolaou G. Asymptotic analysis for periodic structures[M]. Rhode Island: American Mathematical Society, 2011.

[16] Li Youyun, Long Shuyao. A finite element model based on statistical two-scale analysis for equivalent heat transfer parameters of composite material with random grains[J]. Applied Mathematical Modelling, 2009, 33(7): 3157-3165.

[17] Han Fei, Cui Junzhi, Yu Yan. The statistical second-order two-scale method for thermomechanical properties of statistically inhomogeneous materials[J]. Computational Materials Science, 2009, 46: 654-659.

[18] Dong Hao, Cui Junzhi, Nie Yufeng. Second-order two-scale computational method for nonlinear dynamic thermo-mechanical problems of composites with cylindrical periodicity[J]. Communications in Computational Physics, 2017, 21(4): 1173-1206.

[19] Yang Zihao, Ma Liang, Ma Qiang. Multiscale nonlinear th-ermo-mechanical coupling analysis of composite structures with quasi-periodic properties[J]. CMC-Computers Materials & Continua, 2017, 53: 219-248.

[20] 高效伟, 王静, 彭海峰, 等. 高等边界单元法: 理论与程序[M]. 北京: 科学出版社, 2015.

Gao Xiaowei, Wang Jing, Peng Haifeng, et al. Advanced boundary element method: theory and program[M]. Beijing: Science Press, 2015.(in Chinese)

[21] Yu Yan, Cui Junzhi, Han Fei. The statistical second-order two-scale analysis method for heat conduction performances of the composite structure with inconsistent random distribution[J]. Computational Materials Science, 2009, 46(1): 151-161.

[22] Neubrand A, Becker H, Tschudi T. Spatially resolved thermal diffusivity measurements on functionally graded materials[J]. Journal of Materials Science, 2003, 38(20): 4193-4201.