全局灵敏度分析的支持向量机方法

张航，李洪双

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016)

0 引 言

结构系统不确定性分析问题主要包括两个方面：结构输出性能的可靠性分析(Reliability Analysis)和输入随机参数的灵敏度分析(Sensitivity Analysis)。其中，灵敏度分析主要是指分析各输入变量的不确定性对结构系统性能响应量的影响[1]。灵敏度分析通常分为局部灵敏度分析[2]和全局灵敏度分析[3]。局部灵敏度分析定义为输入变量取名义值时功能函数对该变量的偏导数[2]，其不能反映输入变量的整个不确定性范围对输出响应不确定性的影响；全局灵敏度分析则可以从输入变量的整个定义范围来衡量该变量对输出不确定性的贡献程度，在工程实际问题上应用更为广泛。

在众多全局灵敏度研究中，最典型的两类方法：一是以A.Saltelli[3]和I.M.Sobol[4]为代表的基于方差的灵敏度分析方法；二是以E.Borgonovo[5]和M.H.Chun等[6]为代表的矩独立灵敏度分析方法。在结构可靠性分析中，通常采用失效概率来评估其可靠性，而在结构可靠性设计中，则更关心输入变量对结构可靠度或失效概率的影响程度的大小。因此，如果能在得到失效概率的同时得到输入变量对失效概率的灵敏度排序是研究人员所期望的。Li L等[7]提出了基于失效概率的全局灵敏度分析方法，并推导了其与基于方差的灵敏度指标之间的关系，为可靠性评估与全局灵敏度分析建立了重要联系。

目前，基于失效概率的全局灵敏度分析的求解方法主要有两种——数值模拟方法[7]和代理模型方法[8]。Wei P等[9]给出了三种计算基于失效概率的全局重要度的数值模拟法，包括直接蒙特卡罗法、重要抽样法(Importance Sampling，简称IS)和截断重要抽样法(Truncated Importance Sampling，简称TIS)。对于航空航天等领域中大型的、复杂的、隐式的结构灵敏度问题，直接蒙特卡洛方法其输出响应通常需要采用有限元软件得到，计算量大且计算效率较低。重要抽样法和截断重要抽样法，虽然计算效率较高，但是设计点个数及其位置的求解困难，致使重要抽样函数难以确定[10]，同时还需要大量的样本量进行计算。代理模型方法仅需少量样本构建近似模型来描述输入输出关系，之后基于代理模型，直接计算灵敏度指标，该方法可有效避免数值模拟方法需要调用大量有限元计算的问题，极大地提高了计算效率，且其计算精度仅依赖于代理模型本身的近似精度。在结构可靠性设计与灵敏度分析领域，常用的代理模型方法有响应面法[11]、Kriging模型[12]和支持向量机[13]等，其中支持向量机因其具有较强的小样本学习能力和泛化能力，已被广泛应用于工程结构设计和分析中。

目前，虽然对支持向量机理论的相关研究较多，但将其作为代理模型应用于结构灵敏度分析的研究却比较少。因此，本文通过基于支持向量机代理模型的方法对结构进行灵敏度分析，并对所建立的方法进行计算精度和效率方面的验证，以期为失效概率全局灵敏度分析提供一种新的可选方法。

1 基于失效概率的全局灵敏度指标

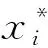
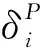
(1)

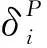
式(1)中灵敏度指标涉及到的两个失效概率PfY和PfY|xi，可通过数值模拟方法求解。

PfY可改写为

=E(IF)

(2)

式中：Rn为n维变量空间；IF为指示函数，当g(x)≤0，其值为1，反之，其值为0。

同理，PfY|xi可改写为

PfY|xi=E(IF|xi)

(3)

将式(2)～式(3)代入式(1)，可得

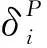
=Var[E(IF|xi)]

(4)

结合全方差公式和式(2)，可以定义基于失效概率的矩独立灵敏度指标为

(5)

式中：Si为主效应。

(6)

式中：x～i为输入变量x中除去xi的其他分量的集合。

2 基于支持向量机的全局灵敏度分析

2.1 支持向量机方法

支持向量机方法(Support Vector Machine，简称SVM)是基于结构风险最小化原则，并建立在统计学习理论的VC维理论的一种机器学习方法。其基本思想为： 对于线性不可分的样本，通过非线性映射φ(·)可以隐式地将欧式空间Rn中的训练数据x映射到高维特征空间Z，从而在高维特征空间上线性可分，如式(7)所示。

Rn→Z,x→φ(x)

(7)

输入向量与输出响应可表示为

(8)

式中：N为训练样本数；wi和b为SVM控制参数；φi(x)为映射所需的函数。

对于任意样本点x，SVM决策函数可以用该点与训练样本之间的映射函数内积<φ(xi)·φ(x)>表示

(9)

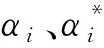
SVM控制参数根据结构风险最小化来确定，通过引入拉格朗日乘子，构造与原始问题对偶的非线性规划问题并求解得到。

当非线性映射φ(x)满足Mercer条件时，可用核函数K(xi,x)代替该内积运算，常用核函数为径向基核函数K(xi,xj)=exp(-‖xi-xj‖2/δ2)，δ为径向基宽度。

因此，式(9)可表示为

(10)

2.2 支持向量机近似模型的构建

综上可知，SVM模型可近似为输入变量x=(x1,x2,…,xn)与输出响应Y的关系，其表达式为

(11)

式中：e为误差。

(12)

训练样本的选取对支持向量机近似模型的精度具有重要影响。对于结构灵敏度问题而言，各随机变量通常服从某一种概率分布。逆变换法是目前应用最为广泛的随机变量产生方法。令随机变量xi的累积分布函数为FX(xi)，根据定义，FX(xi)∈[0,1]，令ui为区间[0,1]上均匀分布的随机数，则由逆分布函数F-1(ui)求得随机变量xi为

xi=F-1(ui)

(13)

直接MCS方法根据随机变量的概率分布进行抽样，可能多次抽样都不出现失效点，而不包含失效点的SVM训练样本集不能全面获取极限状态函数的信息，难以保证近似精度。因此采用拉丁超立方抽样方法在d维[0,1]区间得到样本点后，不采用逆变化方法得到xi，而是将其映射到区间[μi-mσi,μi+mσi]中，以获得更多的失效样本点，从而构建更高精度的代理模型。其中μi和σi分别为随机变量xi的均值和标准差。m值的大小应保证样本中包含一定数量的失效样本点。

为了避免不同量纲的输入变量对SVM训练结果的影响，有必要对样本点进行数据预处理，归一化公式为

(14)

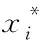
2.3 全局灵敏度指标的求解

采用支持向量机方法代替MCS方法求解全局灵敏度的步骤如下：

(1) 根据输入变量的概率密度函数fX(x)生成两组样本——N×n的随机样本矩阵A和B。其中，N为样本数目，数量为几百到几千不等；n为输入变量的维数。这两组样本可通过简单随机抽样、拉丁方抽样、Sobol序列抽样[15]得到，一般多采用Sobol序列抽样。矩阵阵A和B可表示为

(15)

(16)

(2) 得到另一组N×n的样本矩阵Ci(i=1,2,…,n)，其中Ci的第i列来自于矩阵A，其余的n-1列来自于矩阵B。

(17)

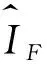
(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

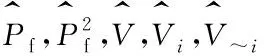
(26)

(27)

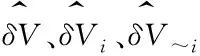
(28)

(29)

(30)

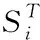
3 算例分析

为了验证本文所提出的方法的性能，对两个数值算例和一个工程算例进行分析。将蒙特卡洛法的结果作为精确解，通过对比失效概率和灵敏度指标的计算结果，以及所使用的样本量来衡量方法的计算精度和计算效率。

3.1 算例1

考虑一个结构系统，其极限状态函数为：

(31)

式中：x1,x2和x3均服从标准正态分布。

使用直接蒙特卡洛法，全局灵敏度排序为：x3>x2>x1。将此结果作为参照解。

分别采用直接蒙特卡洛方法(MCS)、交叉熵方法[16](Cross Entropy Method，简称CE)、支持向机结合蒙特卡洛方法(SVM-MCS)计算输入变量的灵敏度指标。SVM训练样本点为200，映射参数m取4，SVM控制参数采用交叉验证方法获得。基于100次独立运算得到灵敏度指标及失效概率的均值如表1所示。灵敏度主指标计算结果的箱线图如图1所示。

表1 算例1计算结果对比

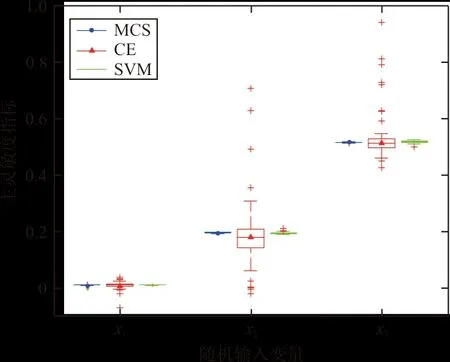
图1 算例1主灵敏度指标箱线图

从表1可以看出：本文所提方法与参照解吻合较好，比CE方法更接近参照解，证明了所提方法的有效性；而且本文所提方法调用极限状态函数的次数也远少于MCS方法和CE方法，表明SVM-MCS方法的计算效率更高。

从图1可以看出：CE方法的数据方差更大，同时有较多的异常数据点，而MCS和SVM-MCS方法明显方差更小，且非常接近，表明所提方法的鲁棒性较高。

综上所述，输入随机变量的灵敏度排序为x3>x2>x1，因此，若能减少输入变量x3的不确定性，便可有效降低结构系统的失效概率。

3.2 算例2

考虑一个包含三角函数的Ishigami函数[17]，其表达式为

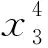
(32)

式中：x1,x2和x3相互独立且都服从(-π,π)的均匀分布，令a=5,b=0.1。

同样采样三种不同的方法计算灵敏度指标，分别独立计算100次。SVM训练样本点为300，映射参数m取4，SVM控制参数采用交叉验证方法获得，计算结果如表2所示(表2计算结果是基于100次独立运算得到灵敏度指标及失效概率的均值)。灵敏度主指标计算结果的箱线图如图2所示。

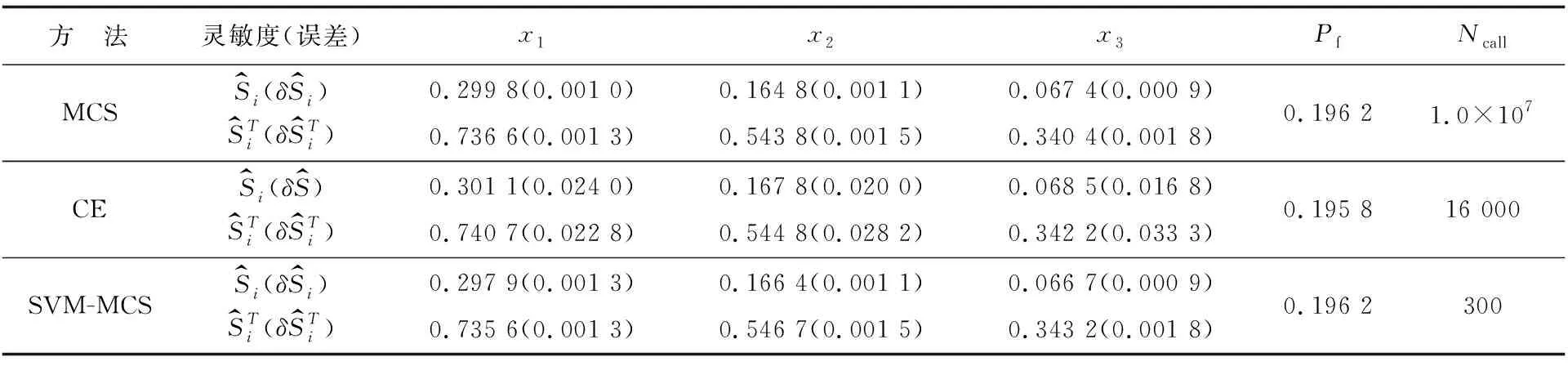
表2 算例2计算结果对比

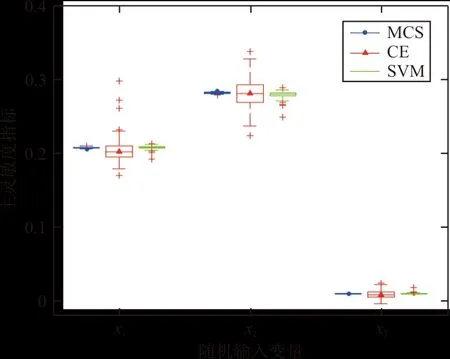
图2 算例2主灵敏度指标箱线图

从表2可以看出：本文方法计算结果、计算误差与参照解更为接近，而CE方法计算结果虽然也较为接近，但其计算误差较大。

从图2可以看出：本文方法的方差较小，具有较高的稳定性。

综上所述，输入随机变量的灵敏度排序为x2>x1>x3，因此，若能减少变量x2的不确定性，便可有效降低极限状态函数的失效概率。

3.3 算例3

考虑如图3所示的九盒段机翼结构[16]，该结构由64个杆单元与42个板单元构成，材料为铝合金，已知外载荷P与各个单元的强度Ri均为正态随机变量，分布如表3所示。原始数据取自文献[18]。通过失效模式的枚举方法可以得到该结构的典型失效模式，对应的极限状态函数为如(式(33))所示。

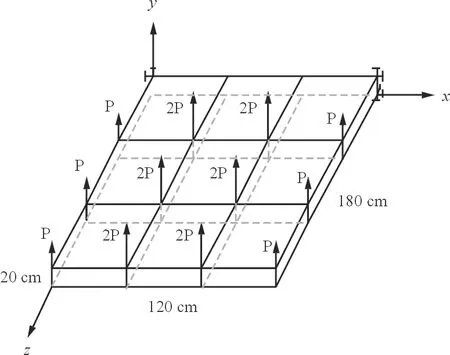
图3 翼盒示意图

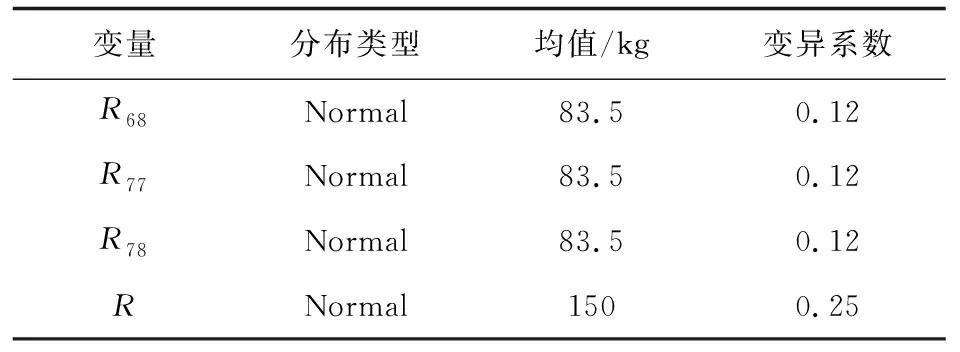
变量分布类型均值/kg变异系数R68Normal83.50.12R77Normal83.50.12R78Normal83.50.12RNormal1500.25

g(R68,R77,R78,P)= 4.0R68-3.999 8R77+

4.0R78-P

(33)

采用三种不同的方法计算得到的灵敏度指标结果如表4所示(灵敏度指标计算结果均值)。所有计算结果基于独立计算100次所得到。SVM训练样本点为400，映射参数 取3.5，SVM控制参数采用交叉验证方法获得。灵敏度主指标计算结果的箱线图如图4所示。

表4 算例3计算结果对比

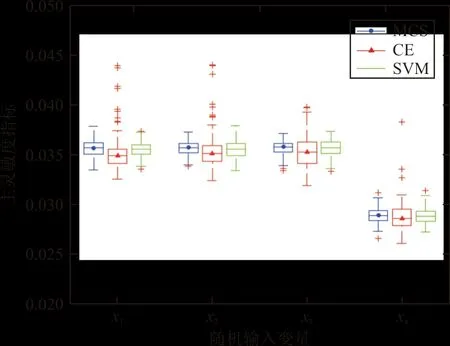
图4 算例3主灵敏度指标箱线图

以 MCS 法的计算结果作为参照解， 从表4可以看出：三种方法的结果吻合很好。 无论是灵敏度排序还是失效概率结果，本文所提方法与MCS 法均一致。从图4可以看出：本文方法的方差较CE方法小，与MCS方法方差接近。但本文所提方法需要调用的极限状态函数仅需400次，相当于CE方法1/65的计算量，MCS方法的1/37 500。因此本文所提方法的计算效率更高。避免了在工程实际问题中，调用大量的、昂贵的有限元计算。

4 结 论

针对基于失效概率的全局灵敏度分析，提出基于支持向量机和蒙特卡洛方法相结合的组合算法。支持向量机方法在小样本下具有较好的泛化能力，能较好的拟合输入变量与输出响应之间的关系，适用于非线性和隐式极限状态函数的灵敏度问题。同时使用均匀映射的方法可以使得更多的样本点落入失效域，提高抽样效率。

通过支持向量机方法与蒙特卡洛方法相结合的组合算法，建立对基于失效概率的全局灵敏度分析框架，可以同时得到失效概率与灵敏度排序，且训练样本少，计算时间短，能够有效的提高计算效率。通过三个算例，验证了所提方法的计算效率和精度，为工程全局可靠性灵敏度分析提供了新工具。

[1] Saltelli A. Global sensitivity analysis: the primer[M]. John Wiley, 2008,304.

[2] 吕震宙. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.

Lü Zhenzhou. Reliability and reliability sensitivity analysis of structural mechanism[M]. Beijing: Science Press, 2009.(in Chinese)

[3] Saltelli A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579-590.

[4] Sobol I M. Sensitivity estimates for nonlinear mathematical models[J]. Matem Mod, 1993, 2(1): 112-118.

[5] Borgonovo E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784.

[6] Chun M H, Han S J, Tak N I. An uncertainty importance measure using a distance metric for the change in a cumulative distribution function[J]. Reliability Engineering & System Safety, 2000, 70(3): 313-321.

[7] Li L, Lu Z, Feng J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38(38): 40-47.

[8] Borgonovo E, Castaings W, Tarantola S. Model emulation and moment-independent sensitivity analysis: an application toenvironmental modelling[J]. Environmental Modelling & Software, 2012, 34(8): 105-115.

[9] Wei P, Lu Z, Hao W, et al. Efficient sampling methods for global reliability sensitivity analysis[J]. Computer Physics Communications, 2012, 183(8): 1728-1743.

[10] 任超, 李洪双. 基于失效概率的全局重要性测度分析的交叉熵方法[J]. 西北工业大学学报, 2017, 35(3): 536-544.

Ren Chao, Li Hongshuang. Cross-entropy method for failure probability based global importance measure analysis[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 536-544.(in Chinese)

[11] 闫明, 孙志礼, 杨强. 基于响应面方法的可靠性灵敏度分析方法[J]. 机械工程学报, 2007, 43(10): 67-71.

Yan Ming, Sun Zhili, Yang Qiang. Analysis method of reliability sensitivity based on response surface methods[J]. Chinese Journal of Mechanical Engineering, 2007, 43(10): 67-71.(in Chinese)

[12] Lee I, Choi K K, Zhao L. Sampling-based RBDO using the stochastic sensitivity analysis and dynamic kriging method[J]. Structural & Multidisciplinary Optimization, 2011, 44(3): 299-317.

[13] 马超, 吕震宙. 基于支持向量机回归的结构系统可靠性及灵敏度分析方法[J]. 固体力学学报, 2007, 28(4): 415-419.

Ma Chao, Lü Zhenzhou. Reliability and sensitivity analysis method of structural system based on support vector machine regression[J]. Journal of Solid Mechanics, 2007, 28(4): 415-419.(in Chinese)

[14] Cui L J. Moment-independent importance measure of basic random variable and its probability density evolution solution[J]. Chinese Science: Technical Science, 2010, 53(4): 1138-1145.

[15] Sobol I M. Uniformly distributed sequences with an additional uniform property[J]. Ussr Computational Mathematics & Mathematical Physics, 1976, 16(5): 1332-1337.

[16] 吕震宙. 不确定性结构系统的重要性分析理论与求解方法[M]. 北京: 科学出版社, 2015.

Lü Zhenzhou. The importance analysis theory and solution method of uncertain structural system[M]. Beijing: Science Press, 2015.(in Chinese)

[17] Steiner G, Zangl H, Watzenig D. Generic statistical circuit design based on the unscented transformation and its application to capacitive sensor instrumentation[C]. IEEE International Conference on Industrial Technology, 2005.

[18] 宋笔锋. 结构体系失效概率计算方法研究[D]. 西安: 西北工业大学, 1994.

Song Bifeng. Study on failure probability calculation method of structural system[D]. Xi’an: Northwestern Polytechnical University,1994.(in Chinese)