基于GARCH模型的股票市场波动预测——以沪深300指数为例

刘浩宇

（格拉斯哥大学，英国 格拉斯哥市 G12 8QQ）

一、研究背景和意义

股票市场是金融市场中比较重要的一个组成部分，它是已经发行的股票转让、买卖和流通的场所，包括交易所市场和场外交易市场两大类别。由于它是建立在发行市场基础上的，因此又称作二级市场。股票市场的结构和交易活动比发行市场（一级市场）更为复杂，其作用和影响力也更大。股票市场最早存在于1602年荷兰人在阿姆斯特河大桥上进行荷属东印度公司股票的买卖，而正规的股票市场最早出现在美国。在中国存在上交所和深交所两个股票交易场所。如今在中国就存在近两亿股民，股票的波动起伏会影响到许多产业和资产。人们就开始研究股票指数和波动，股票的波动看似毫无规律，其实内在存在很多关系，比如长记忆性。这些特性可以用计量经济学，时间序列和随机过程进行分析和预测。

计量经济学在从20世纪开始逐渐兴起。Engle（1982）①提出了自回归条件异方差模型ARCH，他运ARCH模型研究的是英国通货膨胀率，随后人们发现此类模型可以被运用到其他金融领域如股票市场。在之后的几十年时间中，ARCH模型在不断地进化。Bollersle（1986）对此模型进行了改进，提出了GARCH模型。Terasvirtaet al（2010）在讨论会中提出了关于非线性时间序列的ARCH建模，借鉴了Krugman（1999）年提出的非线性计量模型在汇率中计算的理论。在模拟方面，基于十九世纪后半叶的蒲丰问题，有了比较成熟的模拟方法蒙特卡洛模拟法（MC法）。这是运用了随机数和概率模型，将复杂的事物运动的几何数量和几何特征简化成数学方法加以模拟。蒙特卡洛模拟被广泛的运用在诸多领域如教育，军事和金融。股票市场存在随机性，蒙特卡洛模拟正是随机过程的一种模拟方法。

随着近十年金融市场的快速发展，人们逐渐意识到金融市场的波动是可以预测和分析。然而在传统的计量经济学对时间序列的第二个假设中，时间序列变量的波动幅度（方差）是固定的。这当然是不符合实际的，股票收益的波动幅度是随着时间变化而变化的，并不是一个常数。所以需要有新的模型进行解释和分析这种波动。这篇文章运用GARCH模型和蒙特卡洛模拟分析对于具体的股票市场的波动率分析。并且进行运用此时间序列模型对股票波动进行合理的预测。

二、时间序列方法和模型

（一）时间序列的预处理

1.平稳性检验

一个平稳的时间序列过程的概率分布与时间的位移无关。如果从序列中任意取一组随机变量并把这个序列向前移动h个时间，其联合概率分布保持不变。

2.纯随机检验

检验一个时间序列是不是具有纯随机性的方法称为纯随机检验。纯随机序列也成为白噪声序列，他满足各序列值没有关系，γ（K）=0，∨K≠0。在某些情况中，自相关系数波动于0左右的时间序列是纯随机序列。②

3.单位根检验

当今，单位根检验方法为时间序列平稳性检验的最常用方法。单位根检验是构造单位统计量，通过检验特征根是在单位圆上(外)还是单位圆内得出相应结论。如果全部都在圆外表示数据具有平稳性，如果有一个在圆内即表示数据不具有平稳性。GARCH模型虽然是广义ARCH模型，可是仍然可以运用传统的单位根检验进行检验。③DF检验只适用于低阶AR模型，人们进行改进提出了增广ADF检验可以检验高阶AR模型。如果AR(p)序列存在单位根，那么其自回归系数之和正好等于1。

4.信息准则

（1）AIC准则

AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家Akaika在1973年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。④通常将最优模型定义为使AIC的值达到最小的模型。它是拟合精度和参数未知个数的加权函数：

AIC=2log（模型中极型中极大似然）+2（模型中未知参数个数）.

一般情况下，AIC准则拟合精度和参数个数的加权函数

（2）BIC准则

AIC准则也有不足之处：如果时间序列很长，相关信息就越分散，需要多自变量复杂拟合模型才能使拟合精度比较高。为了弥补AIC准则的不足，Akaike于1976年提出BIC准则。Schwartz在1978年根据Bayes理论也提出相同的准则，因此BIC准则又称SBC准则。BIC准则的定义如下：

BIC=2log（模型中极型中极大似然）+log(n)（模型中未知参数个数）.

在实际操作中，将模型的AIC值和BIC值分别比较，选取值最小的为最佳模型。⑤本文会用大量有限的数据分析GARCH模型不同阶数的AIC和BIC值，发现GARCH(1,1)模型的AIC和BIC值相对较小。故GARCH(1,1)模型更加符合本课题。

（二）GARCH模型

Bollerslev（1986）年根据ARCH模型又提出了GARCH模型，GARCH模型是一个专门针对金融数据所量体定制的回归模型，除去和普通回归模型的相同之处，GARCH模型对误差进行了进一步的建模。该模型特别适用于波动性的分析和预测，对投资者的决策起到了重要的指导作用，因此被广泛应用于股票市场分析中。⑥

一般的GARCH(p,q)模型可以表示为：

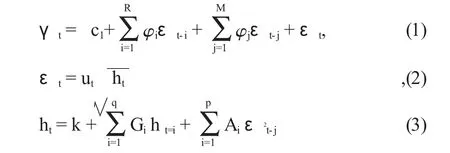
其中ht为条件方差，ut为独立同分布的随机变量，ht与 ut互相独立，ut为标准正态分布。（1）式称为条件均值方程；（3）式称为条件方差方程，说明时间序列条件方差的变化特征。

三、实例分析

在20世纪末中国开始有股票交易，如今中国存在两大交易所即上海证券交易和深证证券交易所。本文研究的是沪深300指数，沪深300指数是由沪深证券交易所于2005年4月8日联合发布的反映沪深300指数编制目标和运行状况，并能够作为投资业绩的评价标准，为指数化投资和指数衍生产品创新提供基础条件。沪深300指数计算方法如下：

报告期指数=报告期成份股的调整市值/基日成份股的调整市值×1000

从国泰君安数据库里找到从2008年1月30日到2017年12月29号的数据（见表1）。以这些数据为基础，利用R软件对其进行时间序列分析和预测，分析股票波动。通过GARCH模型和蒙特卡洛模拟分析时间序列分析方法预测2017年的股票波动情况，将其与实际值比较。利用GARCH模型和蒙特卡洛模拟，预测出2018年沪深300指数波动情况。

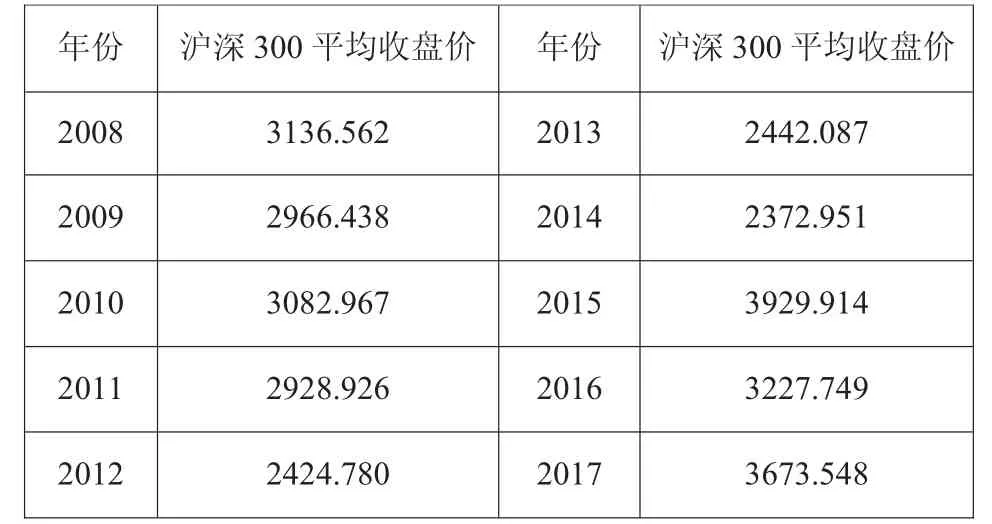
表1 2008-2017年沪深300年平均指数 （元）

从年沪深平均指数可以看书沪深300收盘指数总体存在一个上升的趋势。本文研究是每天的日收盘价，因此选取2008-2017年10年间共计2434天的数据进行分析。

（一）GARCH模型

1.平稳性检验与处理

绘制沪深300收盘价指数2434天的折线图如下：

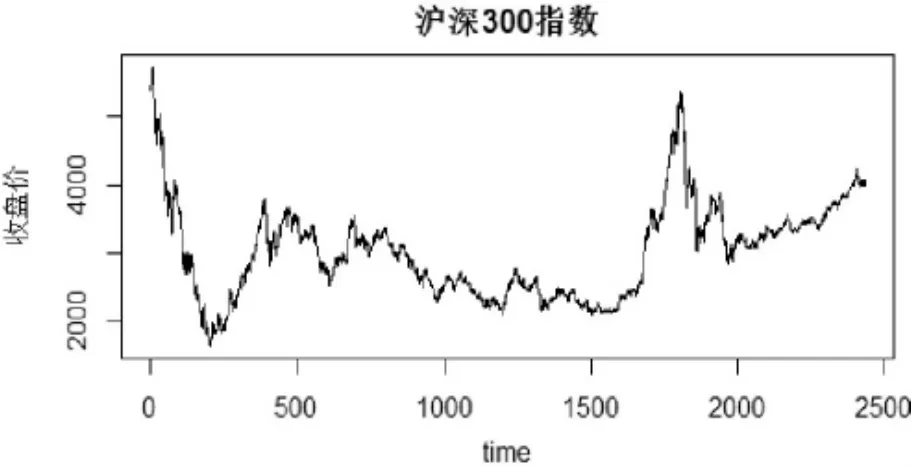
图1 沪深300指数收盘价

由这个沪深300指数的趋势图可知，沪深300指数收盘价围绕某个值在上下波动，可得出一个初步结论这个时间序列是平稳时间序列。然后需要用软件对其进行ADF单位根具体检验，结果如下：

图2 ADF单位根检验

ADF中p值为0.01＜0.05,可知5%显著性水平下拒绝原假设，认为序列沪深300指数是平稳序列。只有当p值大于0.05时，才会认为该序列时非平稳序列。

2.模型的识别和确定

对于GARCH(p,q)模型找到p和q的值，一般会取p=q=1，但这里还会选p=1,q=2和p=2,q=1来进行比较。

确定模型的阶数后还需要进行参数估计和模型检验，以免模型可能存在有效性不足的情况。综合AIC最小、BIC最小，调整最大等原则以及模型残差不相关，对模型完成检验，确定最优形式的GARCH模型，所得结果如下：

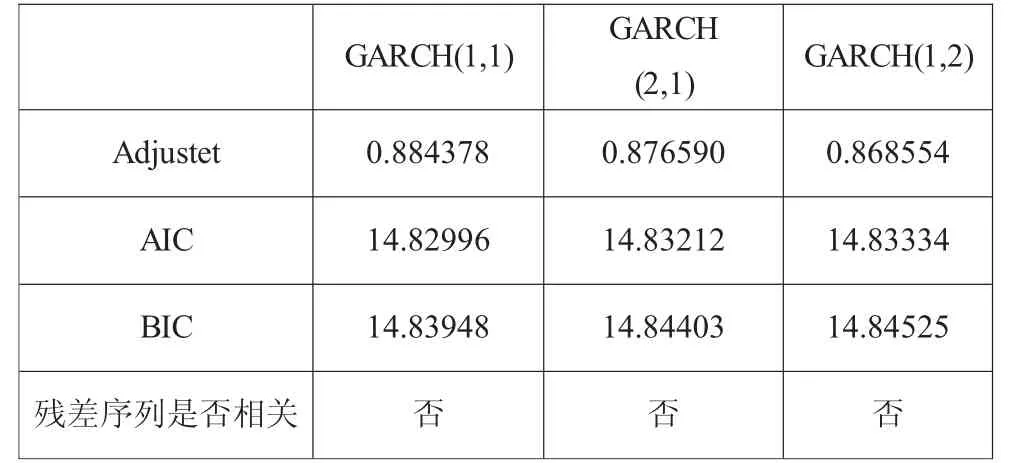
表2 各模型检验结果

经过结果分析可知，所有形式的GARCH拟合模型的残差都不具有序列相关性，即各模型都是显著有效模型。经比较选择拟合度R2较大的，AIC和BIC较小的模型，即p=q=1时模型是最合适的。有参数估计和结果检验（如下图3和图4）知：

图3 参数结果

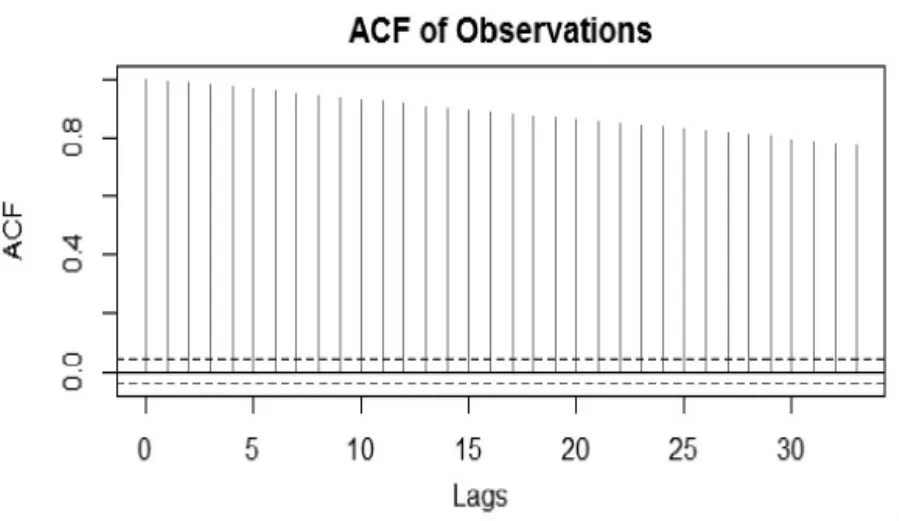
图4 ACF观测值

从图5可以看出沪深300指数的波动并不属于季节性波动，属于趋势波动。在这个结果中知道参数 :μ=3214.11343，ω=1690.85103，α1=0.95362，β1=0.05495,可是发现检验中β1的p值比较大，β1是和残差相关的参数，可能在处理时会出现偏差，根据残差图和正态图（如下），可以得出β1在这里是合理的。因为满足正态分布，残差也符合白噪声序列，模型是合理的。

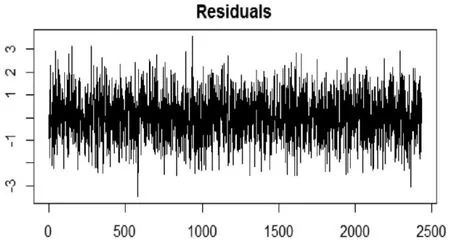
图5 残差图

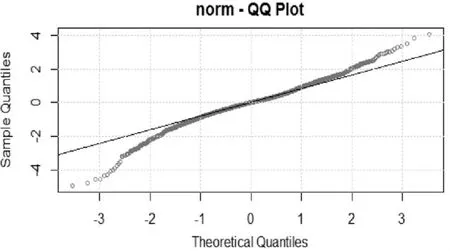
图6 正态分布QQ图

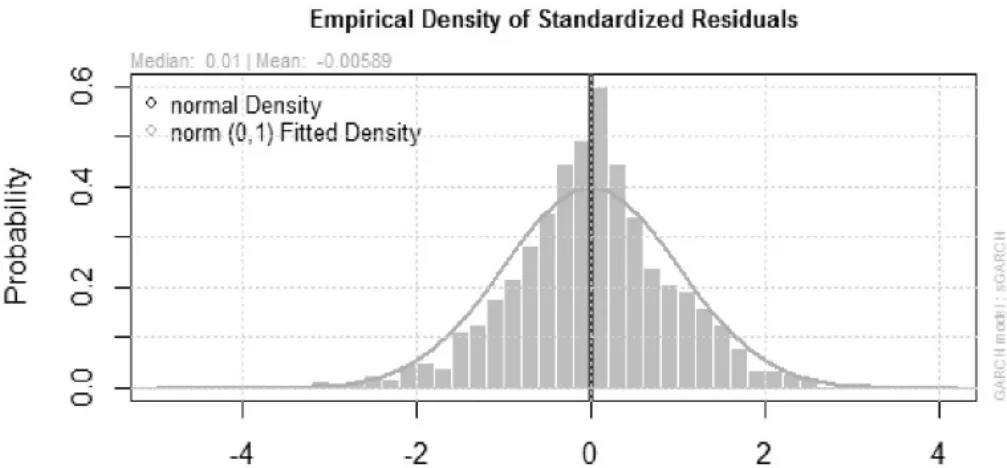
图7 正态分布直方图

3.模型的预测与评价

利用GARCH(1,1)模型对沪深300收盘价指数2018年第一个月（1月2日到1月29日）共计20天的数据进行预测，将2017年12月29日（最后一天）的沪深300指数收盘价4030元作为起始点进行分析，并将预测值与在国泰君安数据库中收集到的真实值做对比，计算出预测的相对误差，得到的结果如下：

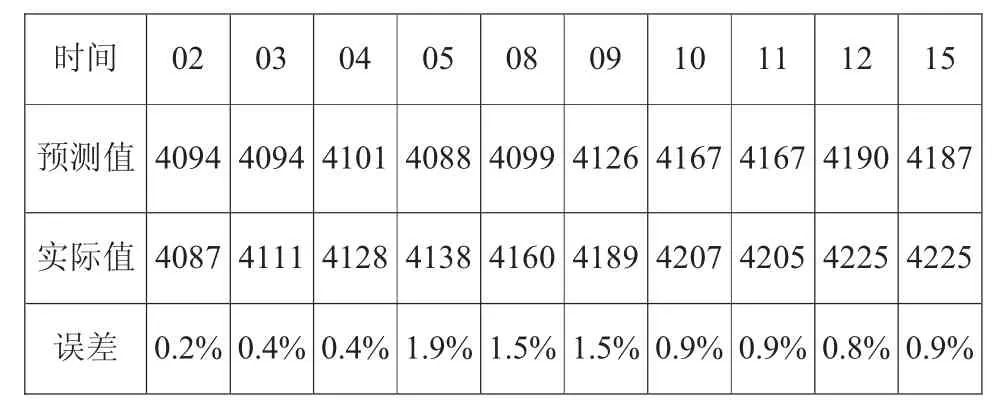
表3 2018年一月沪深300指数实际值和预测值比较

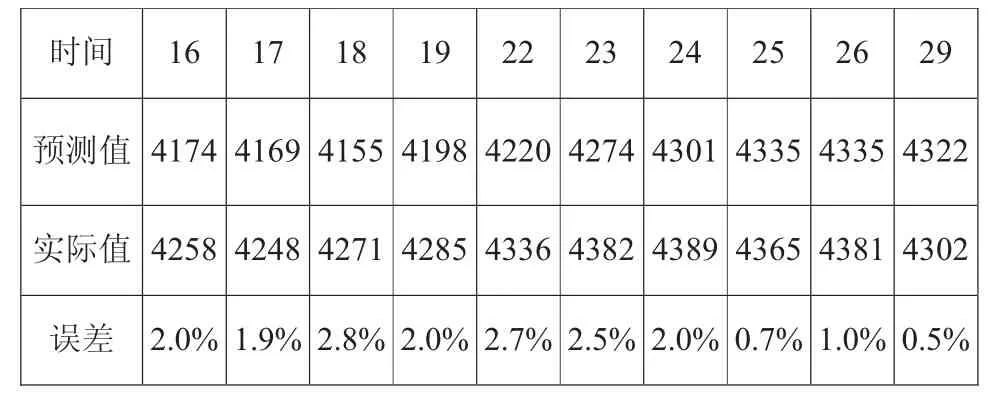
续表3

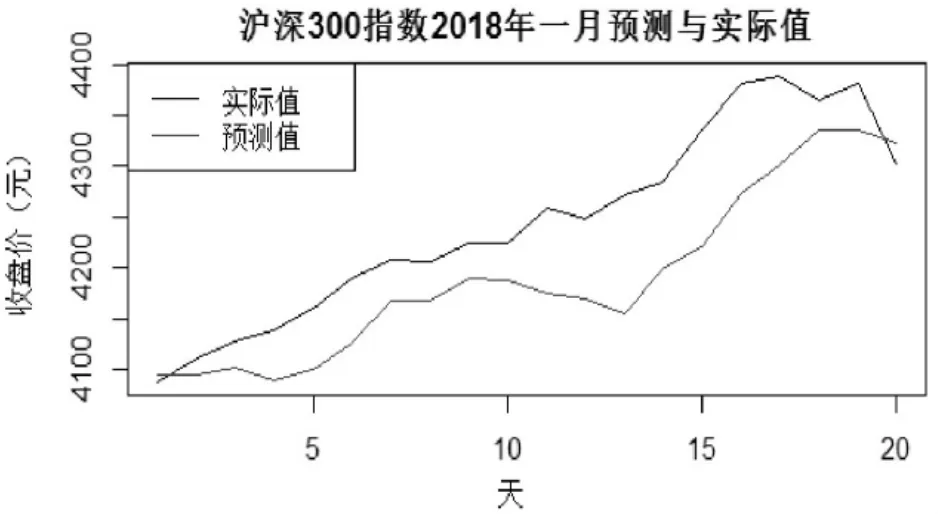
图8 GARCH预测值和实际值

通过观察上述预测误差计算结果可知，GARCH(1.1)模型的存在一定的预误差，可能是由于数据预测有限，可但误差都在5%以内，短期预测值有一定的准确性，从绘制的折现图也可发现实际值和预测值相，都有一个相同的趋势，沪深300指数收盘价呈上升趋势。因此这个模型可以作为分析和预测指数波动的良好工具。下面就会用蒙特卡洛模拟进行进一步的预测和分析。

（二）蒙特卡洛模拟

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数来解决很多计算问题的方法。

在金融领域，蒙卡洛模拟常被运用于期权定价。张峻华等（2014）⑦运用伊藤公式和蒙特卡洛模拟提出了股票波动符合几何布朗运动。由几何布朗运动可知一个运用蒙特卡洛模拟建立的模型：

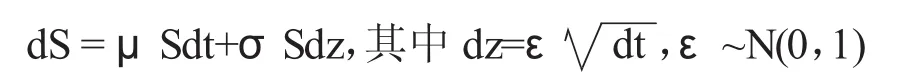
t表示时刻，S表示价格，价格的漂移率为μS，其中μ为常数，运用伊藤引理可知：

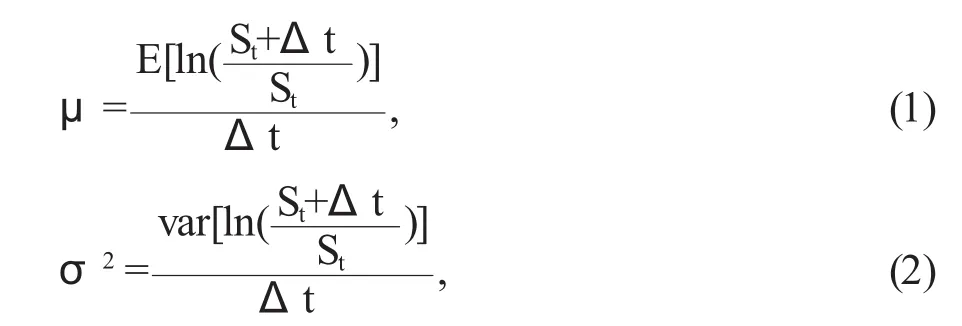
在进行蒙特卡洛模拟前会运用（1），（2）两式得到一天内的预期收益率μ和收益标准差σ2。利用在国泰君安数据库中获得的2008年1月30日到2017年12月29号由GARCH(1,1)模型，计算出μ=0.052%和σ=1.21%。然后对ε～N(0，1)进行随机抽样，由于蒙特卡洛模拟存在一定的偶然性，因此需要多抽几组数据。其中一组的数据如下：

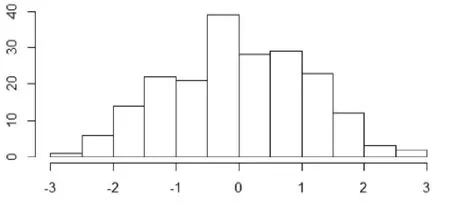
图9 ε的分布

根据直方图发现ε近似标准正态分布与假设一致。在取得ε的样本后，以2017年12月29日的沪深300指数收盘指数为S0=4030，每日指数波动为ΔS=0.052%S0+1.21%Sε

蒙特卡洛模拟操作如下：

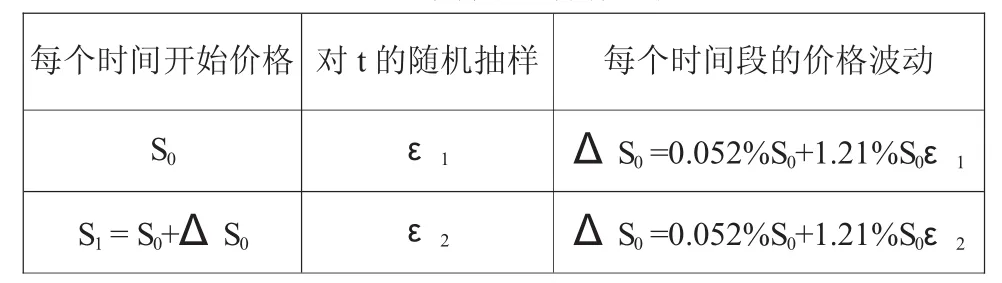
表4 蒙特卡洛操作流程

从多次相互独立的蒙特卡洛模拟中选择一组结合GARCH模型分析图，可以绘制如下沪深300综指价格的波动曲线：

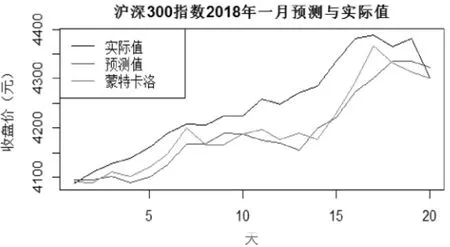
图10 蒙特卡洛结合GARCH模型

根据上述蒙特卡洛模拟过程和折线图可知，经过蒙特卡洛模拟的预测检验和分析下，GARCH模型可以进行拟合沪深300收盘指数，并发现当GARHC模型结合蒙特卡洛模拟得到的预测结果（图12中绿色的线）相对于只有GARCH模型预测结果（图12中红色的线）更加接近真实值。通过分析过去十年的数据，看似沪深300收盘指数波动没有任何可寻规律，可是可以发现总体的趋势是上升的，在2018年第一个月的分析中可以发现虽然有波动总体还是呈上升的趋势。

四、总结

通过本文详细的研究，GARCH模型在股票市场沪深300收盘指数的应用中可以得到以下的结论：

（一）在研究GARCH模型时发现虽然GARCH模型存在众多的阶数，并且每种都可以进行沪深300指数预测分析，但是相比较而言当p=q=1时，即GARCH(1,1)模型的拟合预测效果是最好的。

（二）使用GARCH模型和蒙特卡洛模拟结合的预测比单纯使用GARCH模型的预测值更加精确，以后进行股票收盘价的预测需要将两种方法相结合，虽然蒙特卡洛模拟常用于期权定价，可是金融市场具有互通性，在这里蒙特卡洛模拟和GARCH相结合就完美的预测了沪深300收盘价指数的波动。

（三）GARCH模型可以很好的拟合和预测沪深300收盘指数的波动，因此投资人政府监管机构可以根据GARCH模型的预测结果进行合理的投资和监管。

（四）沪深300收盘指数大体呈上升的趋势，造成该现象的可能原因有1.近十年来越来越多的市民投生到股票市场中，推动了沪深300的发展；2.中国近十年经济发展迅速，强烈的刺激了股票市场，使股票市场呈现了上升的趋势。3.当大盘指数不稳定时，政府会适当对股票进行调控保持它们上升的趋势。⑧

（五）沪深300指数的波动表明在中国这种具有弱式效应的金融市场下，股票波动存在长记忆性，短期波动也具有相关性。

可是在研究的过程中仍然存在一定的问题和缺陷：

（一）GARCH模型不能解释股票收益和收益变化波动之间出现的负相关现象。GARCH(p,q)模型假定条件方差是滞后残差平方的函数,因此,残差的符号不影响波动,即条件方差对正的价格变化和负的价格变化的反应是对称的。然而在经验研究中发现,当利空消息出现时,即预期股票收益会下降时,波动趋向于增大;当利好消息出现时,即预期股票收益会上升时,波动趋向于减小。GARCH(p,q)模型不能解释这种非对称现象。⑨

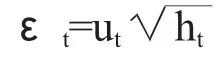
（三）本文选取的是近十年的数据，然而预测数据选取的仅仅是2018年一月份的预测，虽然分析中没发现季节性波动，但是实际中会存在季节性问题，因此要想得出此模型是否可用于未来沪深300指数波动的结论还为时尚早，需要进行大量模拟预测分析。

（四）影响中国股票的因素较多，GARCH模型只是简单的分析了波动，如果想要研究更加深入的话可能还需要分析更多的因素，这样可能需要用其他方法例如主成分分析法和独立成分分析法等方法来进行分析。

【注 释】

①Engle.Robert F..Autoregressive conditional heteroskedasticity with estimates of thevarianceof United Kingdom inflation[J].Econometrica,1982,50.987.1007

②刘毅睿.高斯白噪声序列的检验 [D].中国科学技术大学,2004.

③鲜思东,彭作祥.具有GARCH(near-IGRACH)-normal误差项时序的ADF单位根检验 [J].重庆工商大学学报 (自然科学版),2007(05):459-463.

④鲁万波,余竞.用AIC准则识别最佳因子分析模型[J].成都大学学报(自然科学版),2003(02):28-32.

⑤陈晓锋.AIC准则及其在计量经济学中的应用研究[D].天津财经大学,2012.

⑥魏洁,韩立岩.GARCH模型下基于偏最小二乘的欧式股指期权定价——来自香港恒生指数期权市场的证据[J].数理统计与管理,2015,34(03):550-560.

⑦张峻华,戴伦,刘文浩.股票价格行为关于几何布朗运动的模拟——基于中国上证综指的实证研究[J].财经界(学术版),2014(19):31-33.

⑧马薇,张卓群.结构性改革下政府调控对于股票市场的影响分析[J].河北经贸大学学报,2016,37(04):92-97.

⑨吴亮.沪深300股指期货风险测度研究 [D].南京理工大学,2016.

⑩程聪.基于GARCH/SV模型的结构非线性损伤识别[D].暨南大学,2013.

[1]程聪.基于GARCH/SV模型的结构非线性损伤识别[D].暨南大学,2013.

[2]丛超,徐德玲,庞世达,孙凯旋.基于Matlab的股票市场收益率波动分析实验[J].实验科学与技术,2014,12(05):66-70+73.

[3]陈实.基于平稳过程和技术分析的交易策略研究[D].华东师范大学,2017.

[4]陈晓锋.AIC准则及其在计量经济学中的应用研究[D].天津财经大学,2012.

[5]陈宇,陈怀海,李赞澄,贺旭东.时变AR模型的一种定阶方法[J].振动与冲击,2012(31):158-163.

[6]邓露.长记忆理论及其在金融市场建模中的应用[D].南开大学,2009.

[7]杜娟,何平,向红,蒋励,周藜.离散型计量资料的统计描述和差异的显著性比较，微量元素与健康研究，http://kns.cnki.net/kcms/detail/52.1081.R.20171214.1009.062.html.2018-01-27

[8]高可佑,王潇怡,黄勇兵.沪深300指数的VaR风险测量——基于历史模拟法和蒙特卡罗模拟法[J].市场周刊(理论研究),2008(03):90-91.

[9]韩超.基于时间序列分析的短时交通流量实时自适应预测[D].北京工业大学,2004.

[10]金成晓,曹阳.基于非参数ARCH模型的沪深指数波动性研究[J].山西大学学报(哲学社会科学版),2014(37):62-67.

[11]刘江伟.金融时间序列VaR模型研究与Web可视化系统构建[D].华东交通大学,2015.

[12]刘毅睿.高斯白噪声序列的检验 [D].中国科学技术大学,2004.

[13]鲁万波,余竞.用AIC准则识别最佳因子分析模型[J].成都大学学报(自然科学版),2003(02):28-32.

[14]马薇,张卓群.结构性改革下政府调控对于股票市场的影响分析[J].河北经贸大学学报,2016(37):92-97.

[15]汪卢俊.STAR-GARCH模型的理论与应用研究[D].南开大学,2014

[16]万建强,文洲.ARIMA模型与ARCH模型在香港股指预测方面的应用比较[J].数理统计与管理,2001(06):1-4.

[17]魏洁,韩立岩.GARCH模型下基于偏最小二乘的欧式股指期权定价——来自香港恒生指数期权市场的证据[J].数理统计与管理,2015(34):550-560.

[18]吴亮.沪深300股指期货风险测度研究[D].南京理工大学,2016.

[19]吴霖.基于GARCH模型的股票市场价格波动分析[J].价值工程,2010(29):50-52.

[20]夏若雯,程宇.基于ARIMA-GARCH模型对上海银行间隔夜拆放利率的实证分析[J].商业经济,2016(05):130-132+137.

[21]鲜思东,彭作祥.具有 GARCH(near-IGRACH)-normal误差项时序的ADF单位根检验[J].重庆工商大学学报(自然科学版),2007(05):459-463.

[22]徐景昭.基于多因子模型的量化选股分析[J].金融理论探索,2017(03):30-38.

[23]许鑫.稳定汇率与提升市场效率如何兼得[N].上海证券报,2015-09-16(A02).

[24]闫会强,夏霄松,金浩.HAR族模型对波动率的预测精度比较及其SPA检验——基于沪深300指数高频数据[J].经济论坛,2017(11):75-84

[25]张峻华,戴伦,刘文浩.股票价格行为关于几何布朗运动的模拟——基于中国上证综指的实证研究[J].财经界(学术版),2014(19):31-33.

[26]张普,吴冲锋.基于非参数蒙特卡罗模拟的股票波动性价值研究[J].管理科学,2009(22):89-95

[27]赵婕伶.基于GARCH模型的股票市场波动研究——以沪深300指数为例[J].商,2016(07):212+203

[28]钟锦源,张岩,文福拴,杨明,张小易,朱海兵.利用电气量和时序信息的改进Petri网故障诊断模型 [J].电力系统自动化,2015(39):152-159.

[29]Bauwens L,Laurent S,Rombouts JV K.Multivariate GARCH models:asurvey[J].Journal of applied econometrics,2006(21):79-109.

[30]Box G.Box and Jenkins.Time series analysis,forecasting and control[J].A Very British Affair,ser.Palgrave Advanced Texts in Econometrics.Palgrave Macmillan UK,2013:161-215.

[31]Dziuban CD,Shirkey EC.When isacorrelation matrix appropriate for factor analysis?Some decision rules[J].Psychological bulletin,1974(81):358-361.

[32]Engle.Robert F..Autoregressive conditional heteroskedasticity with estimatesof the varianceof United Kingdom inflation[J].Econometrica,1982(50):987-1007

[33]Kothari SP,Shanken J.Book-to-market,dividend yield,and expected market returns:A time-seriesanalysis[J].Journal of Financial E-conomics,1997(44):169-203.

[34]Stock J H,Watson M W.Business cycle fluctuations in US macroeconomic time series[J].Handbook of macroeconomics,1999,1:3-64.