速率理论在核燃料模拟计算中的应用现状与展望

刘 晶， 谢 鑫， 张文华， 张 博， 恽 迪

(西安交通大学 核安全与运行研究室， 西安 710049)

在早期的核燃料性能分析计算中，对复杂机理过程的建模通常采用经验关系式或半经验的方法，但是该方法只能适用于有实验数据的工况，对于没有实验数据的工况则无法适用。为了提高燃料性能分析的适用范围，尤其是事故工况下的分析，在分析物理机理的基础上，建立机理性模型是燃料性能分析计算的重要方式。速率理论源于化学反应速率理论，其核心是速率常数的确定。而速率常数与反应物质的浓度无关，可由实验直接测得。速率理论源于实验，贴近实验本征特性，与经验模型相比具有更广泛的适用范围。在微观机制尚不明确的情况下，可基于实验结果对物理现象进行描述、预测和分析，因此速率理论在核燃料的性能分析领域得到了迅速发展。

为了促进速率理论在核燃料性能分析计算中的应用，对国内外速率理论在核燃料模拟计算中的相关研究进行了调研，总结了速率理论在模拟计算裂变气体释放率、包壳空洞肿胀速率和辐照生长应变率时的应用方法，同时分析了目前存在的问题以及未来改进和研究的方向，为核燃料性能分析和机理性模型的建立和模拟计算提出了新思路。

1 速率理论简介

速率理论最初源于化学反应速率理论，化学反应速率是指在一定条件下单位时间内某化学反应的反应物或生成物的浓度变化值。在一定温度下，对于基元反应aA+bB=gG+hH，反应速率正比于反应物浓度的乘积[1]，可表示为

(1)

式中，R为反应速率；CA和CB表示两种反应物质A和B的分子浓度，a和b表示反应物的化学计量系数；k为比例常数，称为反应速率常数，其单位与反应化学计量系数相关。反应速率常数与反应物浓度无关。化学反应速率理论的核心在于速率常数的确定，一般用气体分子运动论(碰撞理论)或量子力学(过渡态理论)的方法，并经过统计平均，导出宏观动力学中速率常数的计算公式。

将化学速率理论推广至对物理过程的模拟，其核心也是对速率常数的确定。早期，速率常数的确定是根据实验反推得到数据，后来随着速率理论的发展，经过不断引入其他的理论机制，如分子动力学、第一性原理等，速率常数才逐步由实验反推过渡到利用理论推导得到。

2 燃料性能分析应用研究现状

燃料的性能分析对燃料的设计运行、安全分析以及堆外实验研究都起着重要作用。性能分析涉及的模拟计算包括温度分布、裂变气体相关计算、棒内压力计算、化学元素(U、Pu等)重分布计算、包壳力学计算和包壳腐蚀计算等。速率理论应用在模拟计算中的一般过程是，首先从机理出发，利用速率理论表达出原子、间隙和空位或其他物质相互之间的反应速率，求解出该物质的浓度，进而再利用数学模型计算出所需的物理量。通过对国内外燃料性能分析相关程序和模型的调研发现[2-12]，速率理论在计算裂变气体释放率、包壳空洞肿胀速率和辐照生长应变率上的应用相对成熟，下面依次介绍速率理论在这几方面的应用方法。

2.1 在裂变气体行为研究中的应用

裂变气体行为研究是核燃料性能分析的重要组成部分。裂变气体释放会导致燃料棒内压升高，对于充He的燃料棒，裂变气体释放还会降低间隙热导率。此外，裂变气体Xe和Kr是稳定的同位素，在燃料中几乎不溶解，并在燃料基体内形成气泡，会伴随显著的肿胀。燃料肿胀会加速燃料棒和包壳的接触，继而加剧燃料与包壳的相互作用，影响燃料寿命。

燃料中裂变气体行为是一个较为复杂的物理过程。燃料晶粒内产生裂变气体原子，一部分气体原子在晶内聚成气泡，另一部分扩散至晶界，在晶界扩散并形成晶界气泡。随着燃耗的增加，晶界气泡互相连通并形成释放通道，裂变气体向自由空间释放。同时，燃料中发生的气泡重溶使气泡中的气体原子全部或部分再次溶解到燃料基体中。本文忽略点缺陷对气体的影响，只讨论气体原子和气泡的行为。裂变气体在晶粒不同位置的行为如表1所列。

在上述裂变气体行为中，气泡形核、气泡吸收气体原子、气泡聚合可以认为是原子与原子、气泡与原子、气泡与气泡之间相互作用的结果。下面针对这3种行为具体介绍如何利用扩散控制的速率理论方法推导出速率常数。

设包含n个气体原子的气泡半径为Rn，该气泡吸收气体原子的俘获半径为Rc，模型如图1所示。

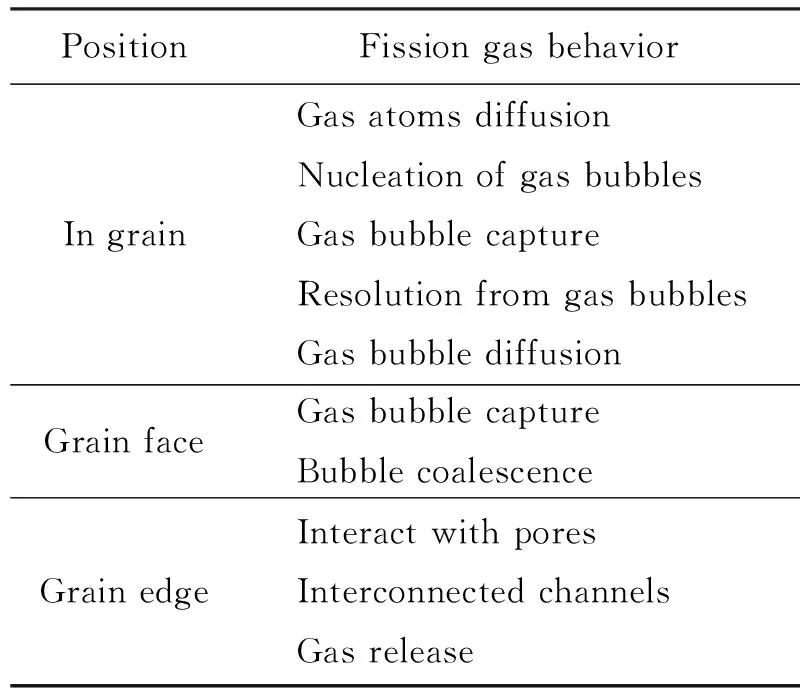
表1 裂变气体在晶粒不同位置的行为Tab.1 Fission gas behavior at different positions

(a) The unit cell for computing the diffusion-controlled rate of point-defect absorption by spherical sinks

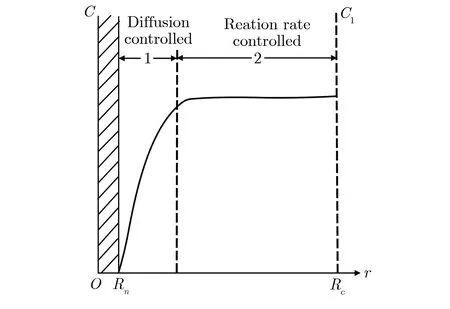
(b) Solution of the diffusion in a spherical shell with a uniform volumetric source

假设气泡静止，且气体原子扩散到达气泡表面就被吸收，那么气泡吸收气体原子的反应速率可表示为气泡表面积和气体原子通量的乘积[2]。

图1(b)中r表示距气泡中心的位置，求解气泡表面至俘获半径处的气体浓度分布，即求解在Rn≤r≤Rc的球壳内的气体原子的扩散方程。构建方程采用了以下几点假设：1)假设气体原子在俘获体积内均匀产生，且除了该气泡中心俘获外，没有其他气泡吸收。在俘获体积内任一点处的气体原子浓度随时间的变化是较为缓慢的，假设俘获体积内产生气体的相对原子质量与被中心气泡吸收的气体相对原子质量相当，即“准稳态近似”；2)气泡表面的气体原子浓度为零且气体原子浓度在气泡表面存在着一个变化的浓度梯度。由于俘获体积半径Rc比气泡半径Rn大得多，在达到俘获半径之前，气体原子浓度就达到了一定值，即气体原子的浓度C1；3)理论上，在区域1内，由于浓度梯度较大，气体原子浓度主要受扩散的限制，区域2受反应速率控制，在建模过程中，假设气泡外均受气体扩散控制，因此忽略源项；4)假设俘获体积是一无限介质。通过以上假设，扩散方程可写为

(2)

式中，D表示气体原子在燃料基体中的扩散系数， cm2·s-1。扩散方程的边界条件为

C(∞)=C1

(3)

C(Rc,t)=0

(4)

最终求解得到被一个气泡吸收气体原子的速率vs,b为

(5)

再乘以气泡浓度Cn，得出所有气泡吸收气体原子的速率vall,b：

vall,b=4πRnD1C1Cn

(6)

对照速率理论式(1)，可得到气泡吸收气体原子的速率常数为

k1,n=4πRnD1

(7)

用类似的方法，可以得出形核的速率常数k1,1及气泡聚合的速率常数ki,j分别为

k1,1=16πR1D1

(8)

kij=4π(Ri+Rj)(Di+Dj)

(9)

目前国际上已研发出多个基于速率理论的裂变气体行为模型。具有代表性的是美国阿贡国家实验室的GRASS-SST[3]、FAST-GRASS[4]，韩国的快堆金属燃料的GRSIS模型[5]和二氧化铀燃料的MEGA模型[6]，俄罗斯核安全研究所(IBRAE)和法国核辐射防护与核安全研究院(IRSN)合作研究的MFPR模型[7]和后续改进的MFPR瞬态模型[8]，Wood和Matthews研究的OGRES模型[9-10]，法国的MARGARET机理模型[11]，瑞士开发的二氧化铀燃料GRSW-A[12]模型，美国开发的氮化铀燃料REDSTONE[13]程序以及米兰理工大学和伊斯坦布尔科技大学合作的没有模拟任何参数的TRANSURANUS模型[14]等。

上述模型都是以速率理论为基础，考虑不同的燃料和工况下裂变气体的行为差异，计算在相应的条件下，不同物质如原子、气泡、点缺陷之间的相互反应，构建裂变气体原子和气泡在晶内和晶界的裂变气体行为方程，最终计算出裂变气体释放率和由裂变气体导致的燃料肿胀。

2.2 包壳的空洞肿胀和辐照生长

速率理论除了可以计算微观尺度下的原子和气泡浓度变化外，还可以计算空位和间隙的浓度变化，模拟出与空位和间隙相关的物理过程。包壳的空洞肿胀和辐照生长与包壳材料的空位和间隙浓度密切相关，因此，速率理论也可以用来模拟包壳的空洞肿胀和辐照生长行为。计算空洞肿胀速率，首先计算空位和间隙的平均浓度。假设只有单空位和自间隙原子是可动的缺陷，小的缺陷团簇是空洞或者环的形核点且这些形核点是固定的陷阱[15]。空位和间隙的浓度变化微分方程分别如式(10)和式(11)所示。

(10)

(11)

式(10)和式(11)中，K0表示产生率，即源项；Ki,vCvCi表示空位和间隙的湮灭速率；求和项分别表示空位和间隙被陷阱吸收的速率。

根据上述与裂变气体行为相似的方法确定速率常数，得到了空位和间隙的浓度。空洞肿胀的速率即空洞体积的增长速率，等于净空位流向空洞的通量，可根据式(12)求得。

(12)

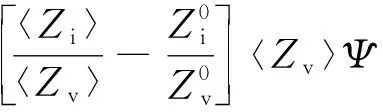
计算辐照生长应变率的方法与计算空洞肿胀速率的方法类似，先用扩散控制的速率理论计算缺陷的浓度，然后通过位错攀移机制计算锆包壳的辐照生长应变率[14]，这里只给出单晶锆包壳辐照生长应变的计算过程，具体步骤如下：

首先计算单晶的空位和间隙的浓度，除了考虑源项、湮灭项外，还要考虑被间隙环、空位环、位错环、位错线吸收的速率。然后再根据得到的缺陷的浓度，计算单晶的辐照生长的应变，a方向和c方向辐照生长的应变率分别为

(13)

(14)

式中，Ailp，Adp，Avlb，Adb分别表示a方向间隙位错环、a方向位错线、c方向空位位错环和c方向位错线的平均应变系数；ρilp，ρdp，ρvlb，ρdb分别是上述4个陷阱的强度。

式(13)表示a方向的应变率，由两部分相加得到，从左到右依次是a方向由间隙位错环产生的应变率和位错线产生的应变率；式(14) 表示c方向的应变率，也是由两部分相加得到，依次是由空位位错环产生的应变率和位错线产生的应变率。

3 速率理论在核燃料模拟计算中的局限性 及研究方向展望

3.1 速率理论在核燃料模拟计算中的局限性

速率理论方法是研究核燃料性能分析的有效工具，但在建模过程中它还存在一些关键和难点问题，主要表现在以下几个方面：

1) 速率常数的确定。 速率常数的确定是速率理论中最核心的问题。在确定速率常数的过程中，为了简化计算，往往采用了一系列的假设。有的假设并不符合实际物理过程，影响了模型的准确性。首先，化学反应速率理论是基于均匀场，而核燃料中发生的反应可能存在于非均匀场。另外，模拟裂变气体的形核过程往往采用扩散控制的速率理论，假设把其中一个气体原子看成是气泡，吸收周围的气体原子，然而在实际物理过程中，气体原子并不是类似气泡和空位的强吸收尾闾，因此用扩散控制的速率理论来模拟形核过程本身就存在一定的问题。此外，有的物质的物理反应机理过程尚不明确，此时往往忽略微观物理作用，采用实验结果倒推等方法来确定速率常数，利用该方法会影响模型的应用范围，因为模型本身带有经验的成分，对数据的验证带来一定的难度。

2) 与速率常数相关参数的确定。速率常数的准确度除了与速率常数的确定方法相关以外，与模拟过程中的其他参数的准确度也有着紧密的联系。如扩散控制的速率理论与扩散系数相关，反应速率控制的速率理论与原子的结合数相关，这些参数本身就是不确定的，不同实验或者不同模型，得出的数值也有所不同。如，氮化铀的扩散系数，采用不同的模型在同一温度下计算得到的扩散系数相差2个量级。因此，与速率理论有关的参数的准确性也会影响着模拟计算的精确度。

3) 缺乏核燃料辐照实验数据。实验数据对模拟计算具有重要的意义，然而在核燃料领域，由于各种原因，大多数实验数据并不公开，这给模拟计算中相关参数的确定和模型的验证带来一定的困难。此外，部分研究的实验本身就是空白，尤其是先进核燃料的辐照实验。因此，在先进核燃料的模拟计算过程中，只能用传统核燃料的辐照实验数据来代替。

3.2 研究方向展望

1) 深入研究物理机理。核燃料所涉及的物理机理十分复杂，仍存在尚不明确原因的一些实验现象。在后续的研究中，对物理机理深入的研究是十分必要的，包括所要计算的物理量与哪些物质有关、这些物质产生哪些反应等。在裂变气体行为机理方面，继续深入研究气体原子和气泡行为，如对气泡形核行为的研究，一方面可以继续研究不同燃料在不同温度、不同燃耗下的双原子形核；另一方面，多原子形核相关的研究目前尚属空白，对多原子形核的研究会对气泡形核过程和裂变气体行为的认识具有重要的意义。此外，还可以深入研究燃料的晶体结构和孔隙对裂变气体释放的影响，燃料的晶体尺寸、孔隙率和材料特性等因素影响着裂变气体扩散至晶面，晶面气泡达到晶棱以及晶棱气泡最终释放至自由空间的快慢，对燃料结构的研究有助于深入了解裂变气体释放的动态过程。

2) 准确模拟反应过程。反应过程模拟的准确与否体现在速率常数的准确性上，提高速率常数的准确度十分必要，主要通过3方面来改进：一是恰当地模拟，在众多物理过程中，根据研究确定哪些过程可以忽略，是否需要引入弹性能、焓值等微观机理；二是改进速率常数的表达形式，在确定需要考虑的物理过程和物理量以后，用更贴近实际机理的形式来表达。例如在模拟形核的过程中，可采用反应速率控制的速率理论，而不是基于浓度梯度推导出来的扩散控制速率理论，反应速率控制的速率理论适用于反应物两者尺寸相当、扩散系数相当的物质，更符合气泡形核的反应过程；三是提高与速率常数相关参数的准确性，通过更深入地研究或者实验来获取更精准的参数来提高速率常数的准确性。如速率常数与扩散系数密切相关，通过提高扩散系数的准确度来提高模型的准确性。

3) 丰富实验数据。实验数据对模型的构建和验证都至关重要。模拟计算的物理量相关的实验数据是验证模型最重要的工具，丰富的实验数据不仅可以帮助对模型的理解，还可以辅助判断模型目前存在的问题和不足，而模型相关参数的实验数据可以帮助提高参数的准确度，进而提高模型的准确度。在接下来的研究中，一方面，要完善和丰富辐照数据库，特别是快堆燃料的辐照数据；另一方面，要增加基础理论的实验数据，如支撑研究形核过程的裂变气体原子和气泡的密度分布，再如通过实验来测得核燃料在不同工况下的空隙变化、缺陷变化等，以此来完善裂变气体模型在不同工况下的适用性。通过上述方式，获取更为丰富的实验数据对促进速率理论发展具有重要的意义。

4 结语

综述了速率理论在核燃料模拟计算研究领域中的应用现状，详细介绍了基于速率理论，模拟计算裂变气体释放率、包壳空洞肿胀速率和辐照生长应变率的方法，在此基础上提出了今后模拟计算机理研究和改进速率常数等方面研究的若干建议。进一步的研究，一方面可以深化速率理论在核燃料性能分析模拟计算中的应用，另一方面也可以促进速率理论和方法体系的不断完善。

[1]徐正. 化学反应速率理论导论[M]: 南京: 江苏科学技术出版社, 1987. (XU Zheng. Introduction to Chemical Reaction Rate Theory[M]. Nanjing: Publishing House of Jiangsu Science and Technology, 1987.)

[2]OLANDER D R. Fundamental aspects of nuclear reactor fuel elements[R]. TID-26711-P1, California Univ, Berkeley (USA) Dept of Nuclear Engineering, 1976.

[3]REST J. GRASS-SST: A comprehensive, mechanistic model for the prediction of fission-gas behavior in UO2-base fuels during steady-state and transient conditions[R]. NUREG/CR-0202, Argonne National Lab, IL (USA), 1978.

[4]REST J, ZAWADZKI S A. FASTGRASS: A mechanistic model for the prediction of Xe, I, Cs, Te, Ba, and Sr release from nuclear fuel under normal and severe-accident conditions[R]. NUREG/CR-5840, US Nuclear Regulatory Commission, 1992.

[5]LEE C B, KIM D H, JUNG Y H. Fission gas release and swelling model of metallic fast reactor fuel[J]. Journal of Nuclear Materials, 2001, 288 (1): 29-42.

[6]LEE C B, YANG Y S, KIM D H, et al. A new mechanistic and engineering fission gas release model for a uranium dioxide fuel[J]. Journal of Nuclear Science and Technology, 2008, 45 (1): 60-71.

[7]VESHCHUNOV M S, OZRIN V D, SHESTAK V E, et al.Development of the mechanistic code MFPR for modellingfission-product release from irradiated UO2fuel[J]. Nuclear Engineering and Design, 2006, 236 (2): 179-200.

[8]VESHCHUNOV M S, TARASOV V I. Development of the MFPR model for fission gas release in irradiated UO2under transient conditions[J]. EPJ Nuclear Sci Technol, 2017, 3(4): 2016041.

[9]WOOD M H, MATTHEWS J R. A simple operational gas release and swelling model I: Intragranular gas[J]. Journal of Nuclear Materials, 1980, 91 (1): 35-40.

[10]MATTHEWS J R, WOOD M H. A simple operational gas release and swelling model II: Grain boundary gas[J]. Journal of Nuclear Materials, 1980, 91 (2/3): 241-256.

[11]NOIROT L, MARGARET. An advanced mechanistic model of fission gas behavior in nuclear fuel[J]. Journal of nuclear science and technology, 2006, 43 (9): 1 149-1 160.

[12]KHVOSTOV G, MIKITYUK K, ZIMMERMANN M A. A model for fission gas release and gaseous swelling of the uranium dioxide fuel coupled with the FALCON code[J]. Nuclear Engineering and Design, 2011, 241 (8): 2 983-3 007.

[13]DEFOREST D L. Transient fission gas behavior in uranium nitride fuel under proposed space applications[R] . ADA252577, Air Force Inst. of Tech, Wright-Patterson AFB, OH(United States), 1991.

[14]PASTORE G, LUZZI L, DI MARCELLO V, et al. Physics-based modelling of fission gas swelling and release in UO2applied to integral fuel rod analysis[J]. Nuclear Engineering and Design, 2013, 256: 75-86.

[15]OKITA T, WOLFER W. A critical test of the classical rate theory for void swelling[J]. Journal of Nuclear Materials, 2004, 327 (2/3): 130-139.