分段式高均匀度螺线管的新设计

杨晓亮， 罗光耀， 罗 敏， 黄 华，金 晖， 康 强， 谭 杰

(中国工程物理研究院 应用电子学研究所 高功率微波技术重点实验室， 绵阳 621900)

高均匀度的螺线管广泛应用于核磁共振成像、高精度探测器、粒子加速器、材料学物质性质研究等领域[1-5]。在高功率微波器件和粒子加速器中的螺线管产生的磁场起着约束粒子运动的重要作用。不同的微波器件对磁场的要求不同，最常见的要求为高均匀度和低漏场两种[6-7]。理论上电磁场逆问题是个多解问题，不同的磁场源分布都可以产生相同的磁场分布，但不同磁场源的研制成本和使用功效差异很大，工程上需要综合平衡。因为磁体设计是一个多参数、多目标的结构优化问题[8-9]，所以计算量大，效率较低，尤其在变量较多时更为明显。同样，如果选择约束条件及给定的初值不合理时，也很难得到最优解。本文针对高功率微波引导磁场需求的典型情况，在φ100 mm×800 mm的磁场均匀区内，利用线性规划算法，设计了一种新颖的分段式高轴向均匀度螺线管，新设计的螺线管轴向不均匀度为0.68%，小于常规方法设计的不均匀度9.8%。同时，新设计的螺线管电学参数和机械参数与常规设计相差不大，该种磁场设计计算方法具有很强的适用性。

1 线性规划磁场设计方法概述

依据毕奥-萨法尔定律，励磁电流和磁场强度存在简单的线性关系。因此，如果给定磁场需求，可以依据线性规划程序反算出所需电流。一般首先对磁体载流区进行网格化，网格大小与线材的截面尺寸相同或两者间有一定的数学关系，同时调整可行载流区的边界，在匀场区内取若干个匀场目标点加以约束[9-11]，螺线管载流区网格化如图1所示。

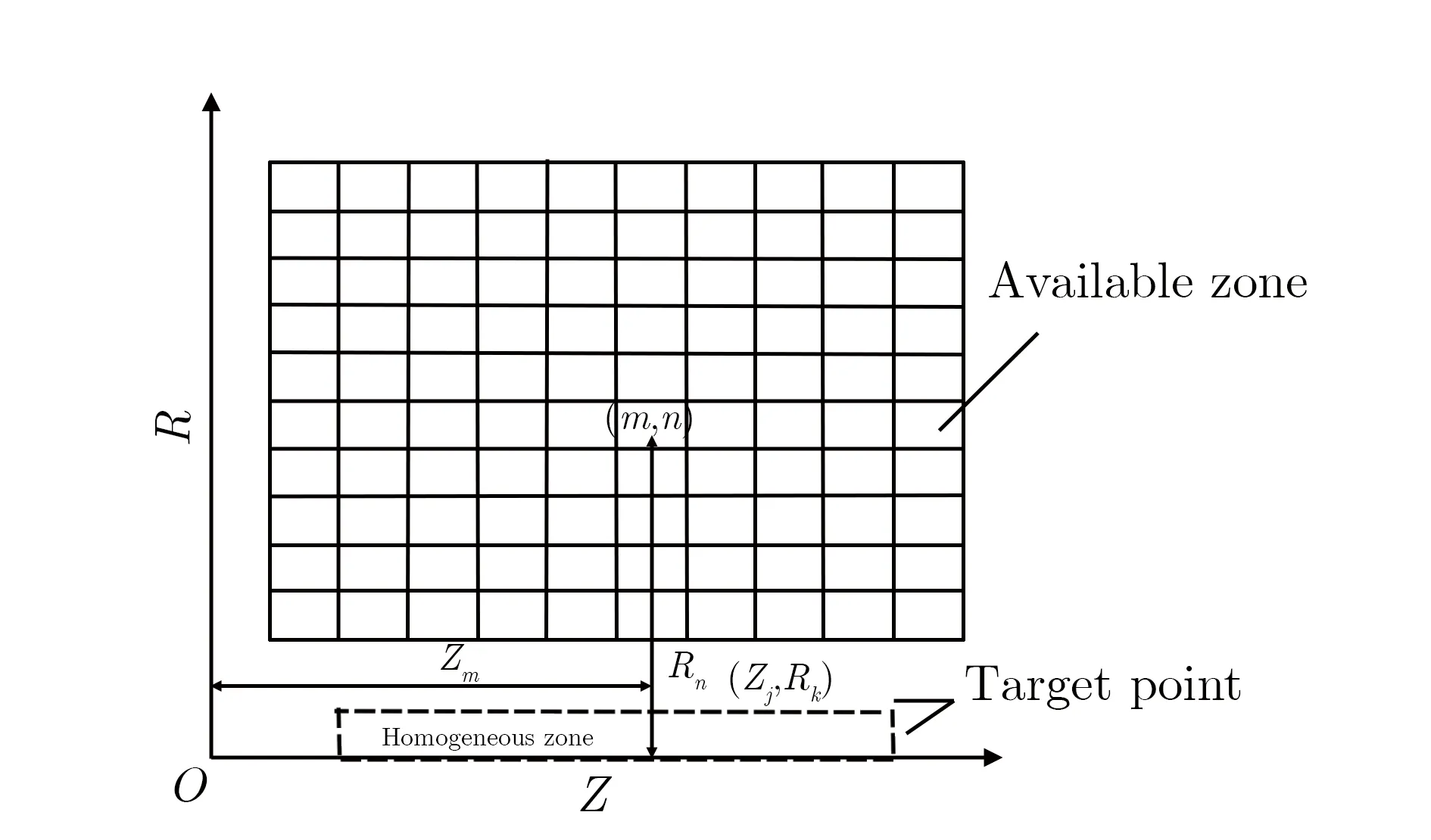
图1 螺线管可行载流区网格化示意图 Fig.1 Mesh grid of available zone in solenoid

O为原点，横轴为螺线管Z轴方向，纵向为径向R方向，可行域Ω在Z和R确定的平面内，剖分为10×10的网格，目标点一般在匀场区的边界上，空间位置为(Zm，Rn)的矩形网格对空间坐标为(Zj，Rk)的目标点上所产生的磁场可由圆环电流丝法求出，具体关系见式(1)：

(1)

式中，Br和Bz分别为目标点的磁场径向与轴向分量；真空磁导率μ0=4π×10-7H·m-1；I为电流；Zm，Rn，Zj，Rk分别对应网格位置和目标点坐标；F(k)和E(k)分别是模数为k的第一类和第二类完全椭圆积分。在目标点的总磁场便是可行载流区内所有网格在该目标点处产生的磁场之和。很显然，这是可行域m×n的网格数对j×k个目标点的线性规划矩阵运算问题。以线圈的总体积为目标函数，磁场均匀度作为约束条件可以求出载流区剖分网格的电流分布。

2 引导磁场设计实例

在高功率微波系统中，以相对论速调管为例，微波器件的波束相互作用区域越长，均匀区就越大，而为了满足某些微波器件的输入输出要求，需要对磁体分段，但分段处的磁场分布会严重影响磁体在均匀区的整体均匀度。要在1 000 mm的轴向长度上产生磁场强度为2 T的磁场，磁体孔径φ为100 mm，均匀区长度为800 mm，但在轴向长度300～330 mm的位置需要馈入微波种子源，使螺线管电流可行域分成两段，但分段处也需保持一定的均匀度，如图2所示。图中包括螺线管可行域A、螺线管可行域B、分割螺线管的馈入波导、发射大功率电子束的二极管、磁场均匀区(对应微波器件的波束相互作用区域)和后端辐射微波的天线。

图2 相对论速调管中的引导磁场 Fig.2 Guiding magnetic field of RKA

2.1 常规螺线管设计

常规的多阶凸凹状螺线管可以在较大的区域产生一定的均匀度，为了从长度100～900 mm、直径φ100 mm×800 mm 的空间内产生2 T的均匀磁场，常规的螺线管线圈设计内孔直径为100 mm，外径约为400 mm，长度为1 000 mm，电流密度40 A·mm-2，而且端部需要典型的匀场线圈。图3显示了常规螺线管模型和中心磁场轴向分布情况。

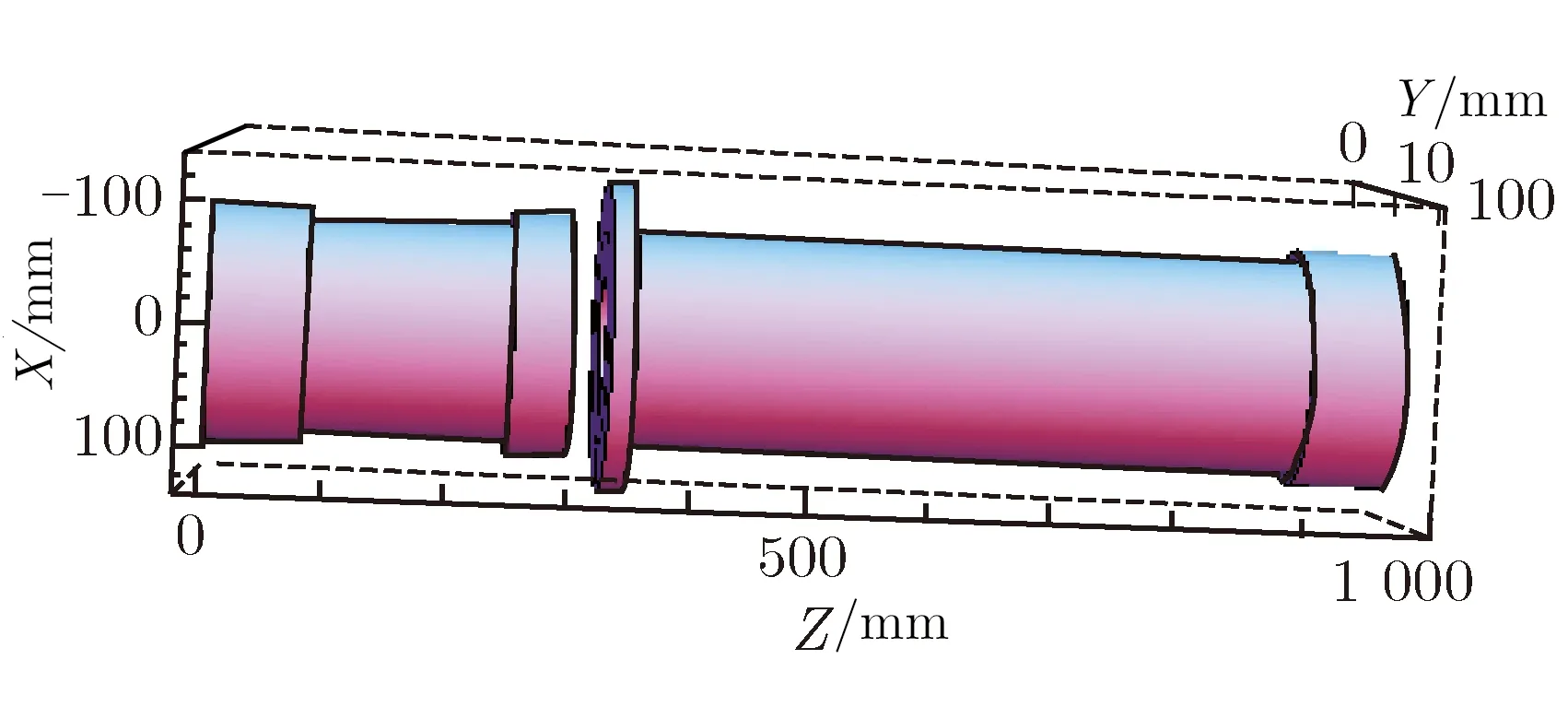
(a) Traditional solenoid model

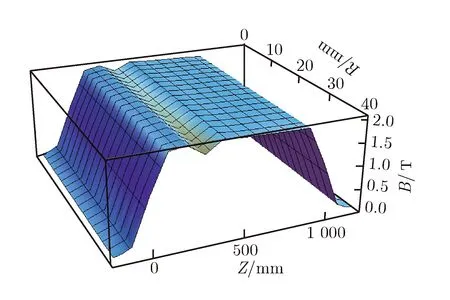
(b) Bz distribution of traditional solenoid

图3常规螺线管模型和对应的轴向磁场分布
Fig.3TraditionalsolenoidmodelandBzdistribution

从图3可以看出，此磁体可以产生磁感应强度平均值为2 T的磁场，但在均匀区内最大值和最小值都在分段处，使得整体均匀度仅有9.8%。螺线管的电磁储能为44 kJ，当用1 mm×1 mm的矩形线缆时，所需电流为40 A，自感约54 H。为了产生2 T的高磁场，共消耗线材约148 kg，磁体中最大场强在内半径处，磁感应强度为2.12 T。为了获得更高的均匀度，一般需要在螺线管外部加多层匀场线圈，均匀度要求越高，匀场线圈越多。在医疗行业的核磁共振成像磁体中，这种有源匀场甚至可以在mm级的均匀区提供10-6的磁场均匀度。除了有源匀场，软磁材料按照某种方式阵列分布的无源匀场也能提高均匀度，有源匀场和无源匀场会使得高均匀度磁场体积庞大，造价昂贵，系统复杂。为了充分对比匀场效果，本文仅考虑同等级别的有源匀场。

2.2 新设计的螺线管

理论上，产生磁场的唯一方式为带电粒子运动，即电流。如果线圈截面可以设计成需要的形状，则可产生各种磁场分布。用较细的矩形或圆形线缆可以组合成复杂的线圈截面，如图4所示，显示了可行域A内剖分网格和每个网格对应的电流密度值。计算时，轴向剖分网格数为120，径向剖分网格数为30，通过MATLAB编程计算的电流密度数值填于网格中。

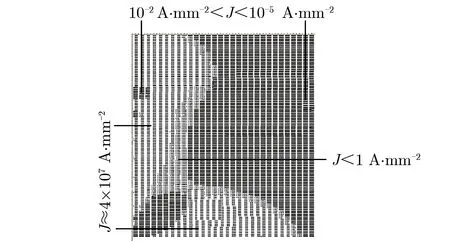
图4 可行域A剖分网格和网格对应的电流密度情况Fig.4 Grids and corresponding current density values of available zone A

通过计算结果可以看到，由于线性规划的特征，通过目标函数的收缩作用使得绝大部分可行域的电流密度趋于两个极端，即最大值4×107A·mm-2和最小值0，而中间值1 A·mm-2较少。通过MATLAB自带的可视化函数显示可行域A对应网格电流密度，根据对磁场的要求计算的可行域电流密度分布，如图5所示。

图5中左上顶点表示螺线管中心，纵轴表示螺线管轴向，横轴表示径向。左侧空白区表示内孔半径，即非载流区域，最右侧颜色条表示电流密度。由于线性规划目标函数的性质，绝大部分可行域内的电流密度只有最大值和最小值两个值。在螺线管的分段位置附近，电流密度区域基本成阶梯状，且电流密度分布不连续，这说明螺线管在分段处需要分离线圈组合，才能产生需要的磁场分布。将螺线管截面的电流密度取最大值的网格用极小的圆环电流丝代替，忽略电流密度数值较小的区域,可以生成新的截面较复杂的螺线管，可行域A段线圈集合(3/4圆环)见图6。

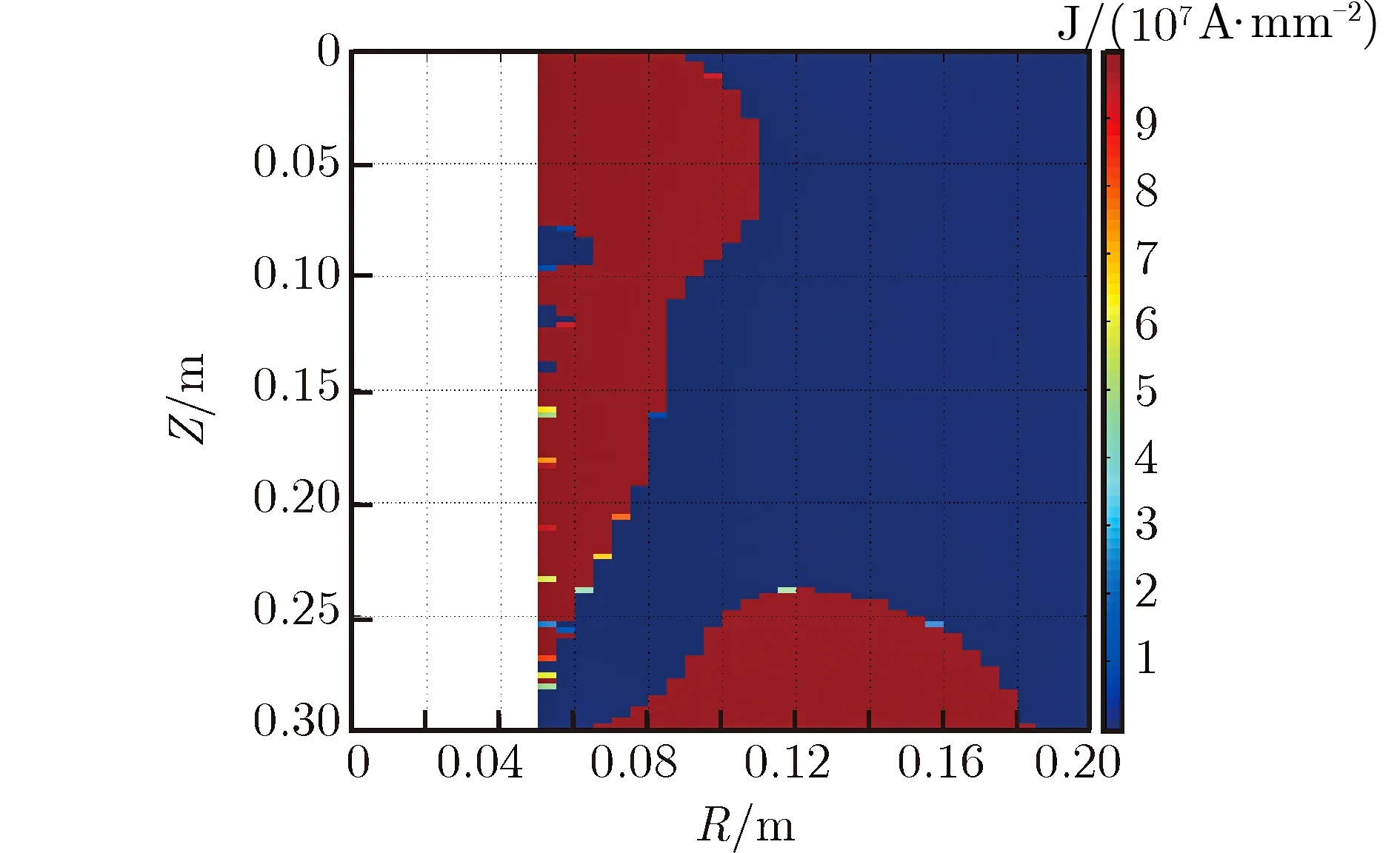
图5 线性规划计算的截面电流密度 Fig.5 Visualization of section current density values calculated by LP method

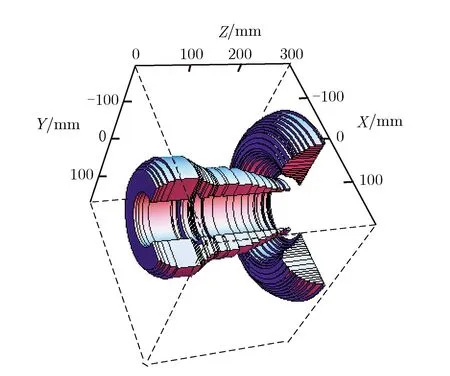
图6 可行域A内的电流密度最大值用圆环线圈代替Fig.6 Zone with the maximum current density in available zone A replaced by ring coils

同理，将两个可行域所有电流密度数值较大的区域用圆环电流线圈代替，新设计的螺线管线圈见图7，在Radia中完成了圆环电流线圈组合后，计算匀场区的轴向磁场分布如图8所示。

通过计算不难发现，在同样的800 mm的磁场均匀度要求的区域，新设计的螺线管磁体线圈不均匀度为0.68%，小于常规螺线管的不均匀度9.8%，新的磁体内径为100 mm，外径为390 mm，总长度为1 000 mm，新设计和常规设计相当。不仅如此，在同样电流密度和线缆线规条件下，新磁体储能为48 kJ，电感为61 H，磁体最大磁场为2.08 T，而所耗线缆约为120 kg，这是因为中间分段处的分立线包增加了均匀度的同时也增加了线缆质量。

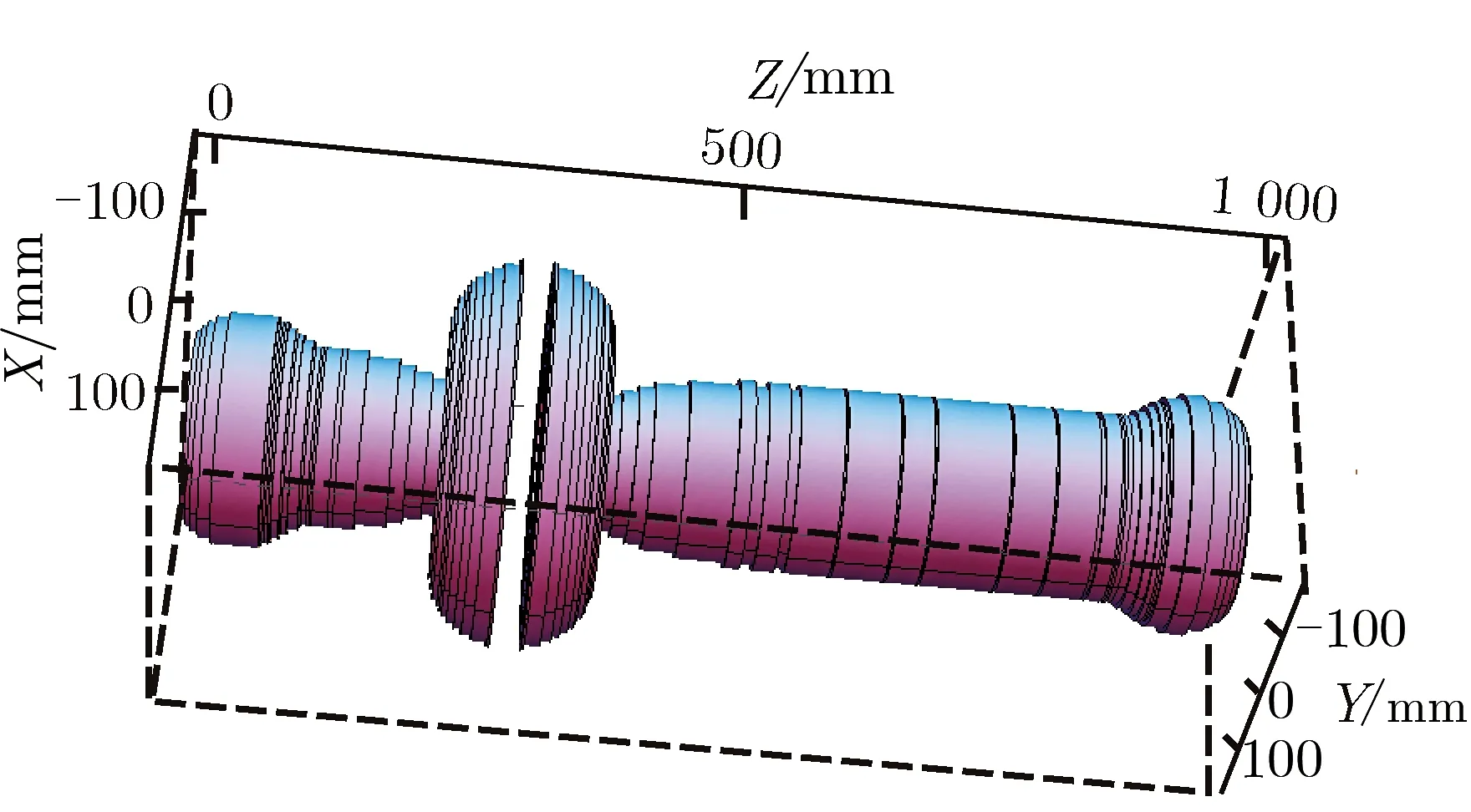
图7 新设计的螺线管磁体线圈Fig.7 New-designed segment solenoid

图8 新设计的螺线管匀场区轴向磁场分布Fig.8 Bz distribution in homogeneity magnetic field of the new-designed segment solenoid

新设计的螺线管需要复杂截面骨架用于容纳新的磁场线圈，一种可行的骨架制造方式是通过分层制造骨架，一边绕线一边叠很薄的骨架，每个切片的薄骨架和每一层的绕线相协调，然后将切片的薄骨架堆叠而成。

2.3 两种设计的对比

和常规的凸凹台阶式螺线管相比，新设计的分段式螺线管磁体有很多优势：首先也是最重要的一点，磁场均匀度大大提高，提高均匀度可以提高微波器件的波束相互作用效果，更容易获得高功率微波。其次，在同等的电流密度和线缆线规条件下，新设计更加充分地利用了电流和线缆，获得同样强度的磁场所消耗的线缆质量变小，实现了小型化和紧凑化。再次，线性规划磁场设计方法具有通用性，依照同样的程序可以实现低漏场设计，很容易移植和推广。 两种螺线管主要设计参数如表1所列。与常规复杂的大型高均匀度磁体相比，新磁体设计有较强的实际应用价值，它明显减少了制造成本，更加充分利用了电流和线缆。但新设计的螺线管骨架更复杂，对绕线工艺的要求更高。

此外，新螺线管设计和制造过程的磁场存在误差，主要因为：1)线性规划所用的是圆环电流丝叠加计算磁感应强度，线性叠加是在剖分很小的情况积分的近似处理，剖分越密，误差越小，但该项误差始终存在；2)线性规划所算出的电流密度分布绝大部分为极值，也有一定数目的网格中间值存在，在磁场设计的过程中忽略了中间值的电流密度，这会造成磁场计算误差；3)在实际制造绕线过程中不可避免地存在工程误差，这也会造成磁场误差。

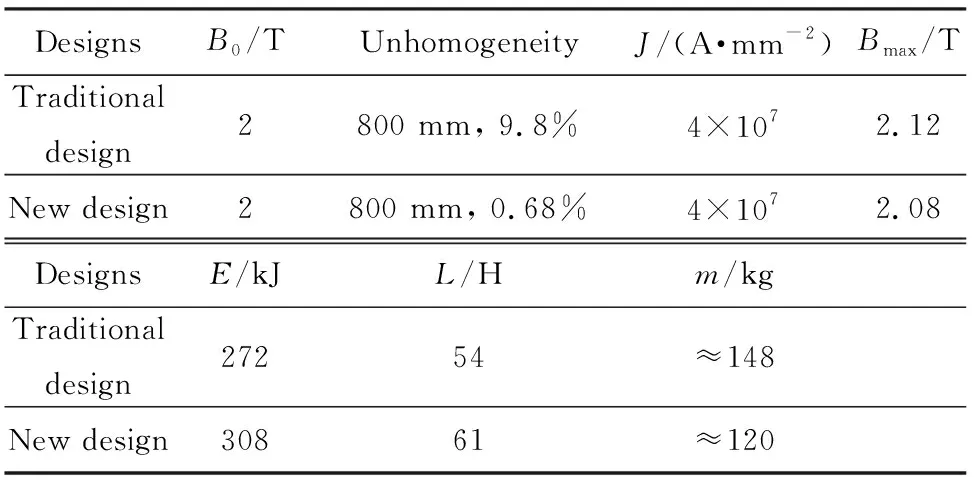
表1 两种磁体设计参数对比Tab.1 Parameter comparisons between traditionaland new-designed magnet

3 结论

利用线性规划算法设计的分段式螺线管可通过改进绕线工艺和机械结构来提高均匀度，并具有很强的推广性，较适合复杂情况下的磁场计算。设计的磁场可应用于高功率微波螺线管型引导磁场，在φ100 mm×800 mm波束相互作用区域内，该螺线管可把常规设计的磁场不均匀度9.8%降低至0.68%，大幅提高了均匀度，能更好地引导粒子束在均匀区内运动。而且，在同样的电流密度条件下，新设计的磁体体积、质量和常规设计相当。该磁场设计方法易于推广到其他磁场约束条件下的磁场设计。但不足是储能稍大，难点在于骨架和冷却机械结构设计更复杂，线圈绕制工艺要求更高。

[1]WANG Q L, XU G X, DAI Y M, et al. Design of open high magnetic field MRI superconducting magnet with continuous current and genetic algorithm method[J]. IEEE Trans Appl Supercond, 2009, 19(3): 2 289-2 292.

[2]荆晓兵, 陈楠, 李勤. 宽平顶低横向场分量螺线管线圈设计[J]. 强激光与粒子束, 2010, 22(4): 591-594.(JING Xiao-bing, CHEN Nan, LI Qin. Design of wide flat-topped low transverse field solenoid magnet[J]. High Power Laser and Particle Beams， 2010, 22(4): 591-594.)

[3]BENFORD J, SWEGLE J. Applications of high power microwaves[C] // 9th International Conference on High-Power Particle Beams, 1992: 341-348.

[4]JEONG E K, KIM D H, KIM M J, et al. A solenoid-like coil producing transverse RF fields for MR imaging[J]. Journal of Magnetic Resonance, 1997, 127(1): 73-79.

[5]TENG J, GU Y Q, ZHU B, et al. Beam collimation and energy spectrum compression of laser-accelerated proton beams using solenoid field and RF cavity[J]. Nucl Instrum Methods Phys Res A, 2013, 729(3): 399-403.

[6]WU Y, XIE H Q, LI Z H, et al. Gigawatt peak power generation in a relativistic klystron amplifier driven by 1 kW seed-power[J]. Phys Plasmas, 2013, 20(11), 1131021.

[7]黄华, 范植开, 谭杰, 等. 长脉冲相对论速调管中束流脉冲缩短的研究[J]. 物理学报, 2004, 53(4): 1 129-1 135.(HUANG Hua, FAN Zhi-kai, TAN Jie, et al. Investigations on beam current pulse shortening in a long pulse relativistic klystron amplifier[J]. Acta Phys Sin, 2004, 53(4): 1 129-1 135.)

[8]张国庆, 杜晓纪, 朱自安, 等. 基于0-1整数线性规划的自屏蔽磁共振成像超导磁体设计[J]. 物理学报, 2012, 31(22): 113102. (ZHANG Guo-qing, DU Xiao-ji, ZHU Zi-an, et al. 0-1 integer linear programming for actively shielded magnetic resonance image(MRI)superconducting magnet design[J]. Acta Phys Sin， 2012, 31(22): 113102.)

[9] DU J J, YUAN P, MA L Z, et al. A novel design methodology for active shim coil[J]. Measurement Science and Technology, 2012, 23(8): 085502.

[10]WU W, HE Y, MA L Z, et al. The optimal design of a 7 T highly homogeneous superconducting magnet for a penning trap[J]. Chin Phys C, 2009, 34(7): 978-982.

[11]YANG X L, MA L Z, WU W, et al. Design of a superconducting magnet for CADS[J]. Chin Phys C, 2012, 36(9): 886-890.