基于主元分析的支持向量数据描述的故障检测
2018-05-30谢彦红刘文静
谢彦红, 刘文静, 李 元
(沈阳化工大学 数理系, 辽宁 沈阳 110142)
随着工业结构的日益复杂化,对运行系统的安全性和可靠性的要求也日益提高[1-3],对设备和系统进行及时有效的监控,是提高设备工作效率和可靠性的有效方法[4-7].目前,以主元分析(principal component analysis,PCA)[8-9]、偏最小二乘(partial least squares,PLS)[10-11]为代表的经典统计方法在使用时仍然存在局限性.PCA只利用了信号的二阶统计信息,在数据不满足完全高斯分布时其检测效果并不理想.独立主元分析(independent component analysis,ICA)[12-13]方法虽然使用了高阶统计量信息,但研究仍然还停留在线性问题上,对线性、非线性混合方面的问题研究还不成熟.Tax[14-15]等人提出了支持向量数据描述(SVDD)方法,该算法可以很好地处理过程混合信息,而且又对非线性问题具有较高的处理能力.虽然SVDD方法有许多优点,但是当样本数据较大时,由于核函数的原因将会导致计算的复杂性明显增加.为了克服这个缺点,提高数据检测效率,降低检测时间,将从降低数据维数和减少样本个数两个方面考虑.本文综合考虑了主元空间及残差空间的特征信息,提出一种对主元空间及残差空间先后建模的故障检测方法,提高检测效率的同时又有效地防止漏检情况的发生.
1 SVDD基本理论
支持数据向量描述[16-17](support vector data description,SVDD)的基本思想是数据集X={xi,i=1,2,…,N},通过某种非线性函数Φ:X→F将原始空间的数据投射到高维特征空间{Φ(xi),i=1,…,N},在高维特征空间中找到一个几乎包含所有数据样本的最小体积超球体,a是超球体的球心,R是超球体的半径.考虑到测量误差或者噪音等干扰引起的离群点影响,引入松弛变量ζi;C是惩罚参数.此问题可描述为:
(1)
上述问题可以转化为解决相应的对偶问题:
(2)
其中a是拉格朗日因子.
用核函数K(xi,xj)代替内积〈Φ(xi)·Φ(xj)〉可以将低维空间的数据向高维空间进行投射:
(3)
利用规划问题求解,可以求出ai,如果0 (4) 对于新的样本xnew,其到超球体球心的距离可表示为: Dnew= (5) 如果Dnew 从以上SVDD的算法可以看出:支持向量数据描述的算法将会转变为一个最优规划的问题,在求解过程中需用到核函数来进行数据计算,算法的复杂度明显增大,随着样本个数的增加,算法的计算量也会呈指数增长,这样一来,当需要计算的数据很庞大时就会产生维数灾难.而且由支持向量机理可知:只有“支持向量”才会对数据的分类起作用,但是支持向量在数据很庞大时所占的比重较小.因此,需要花费大量时间去优化非支持向量,浪费大量的有用计算时间. 主元分析(principal component analysis,PCA)是多元统计过程常用的方法,是将数据的主要信息方向作为新的数据空间的坐标方向,从而达到数据从高维空间向低维空间的变换. (1) 初始化:设数据样本X={x1,x2,…,xM},其中每个样本xi的维数为n. (2) 预处理:对数据样本集X={x1,x2,…,xM}中的每个样本xi∈X进行中心标准化处理,从而得到新的样本集X′. (3) 计算协方差矩阵.根据式(6)计算经过预处理的样本集的协方差矩阵C (6) (4) 计算特征值和特征向量.求上述协方差矩阵的所有特征值λi,当λi≠0时,计算其对应的特征向量pi. (5) 计算累计贡献率并求解各特征值λi的累计贡献率a: (7) 其中:z表示值不为0的特征值的个数.选取贡献率大的特征值所对应的特征向量组成优化特征向量集合为P. (6)主元空间及残差空间的表示如下: (8) 2.2.1 建模描述 首先,在采集的原始数据基础上,通过主元分析进行特征提取,获得维数简约的样本数据;其次,将主元空间和残差空间得分矩阵分别运用SVDD算法确定阙值R1及R2. 2.2.2 检测模型描述 ① 采集故障数据:数据发生故障时在不同的设备中会有不同的表现,在机器设备中,可以将震动信号作为发生故障的信号;在发动机设备中,可以通过振动的频信号作为特征信号. ② 应用PCA方法对采集的数据进行降维,降低数据的复杂度. ③ 利用SVDD算法对主元空间进行故障检测:对主元空间得分矩阵利用SVDD算法进行故障检测,计算其到超球球心的距离D1,如果得到的距离D1大于半径R1,则为故障样本,否则转入步骤④. ④ 利用SVDD算法对残差空间进行故障检测:对残差空间得分矩阵利用SVDD算法进行故障检测,计算其到超球球心的的距离D2,如果得到的距离D2大于半径R2,则为故障样本,如果得到的距离D2小于半径R2,则为正常样本. 建模及检测流程如图1所示. 图1 建模及检测流程Fig.1 Modeling and testing flow chart 首先进行一个数值仿真的实验,然后又对TE过程数据进行实验,验证了该方法的有效性. 过程数据产生如式(9)所示: x1=x2+e x2=x+e (9) 其中:x服从N(0,1)分布,e为噪声,服从N(0,1)分布. 产生700个训练数据,53个测试数据(50个校验数据及3个故障数据).选取第一个变量作为主元,第二个变量作为残差主元.图2为SVDD与PCA-SVDD方法的检测结果. 图2 PCA-SVDD及SVDD检测结果Fig.2 PCA-SVDD and SVDD test results 由图2可以看出:PCA-SVDD的误报数比SVDD明显减少.由支持向量机理可知,只有支持向量对分类起决定的作用,在没有降维的情况下,支持向量所占的比重小,不能进行很好的分类;PCA-SVDD通过主元提取获得更多的支持向量,支持向量所占的比重增大,可以更好地分类,从而降低了误报.另外从检测时间上来看,PCA-SVDD提取出数据的特征,获得维数简约的样本数据,在计算时间上也比SVDD方法的用时短.图3为SVDD及PCA-SVDD各个样本所用时间折线图,可以更加直观地看出两种方法各个样本的用时,证明了PCA-SVDD具有缩短检测时间的优势. 图3 SVDD及PCA-SVDD时间折线图Fig.3 SVDD and PCA-SVDD time line chart Tennessee Eastman过程中共包含有41个测量变量和12个控制变量,其中41个测量变量又可以划分为22个过程测量变量以及19个成分测量变量.在应用过程验证监控方法性能时,一般选择22个连续过程测量变量和12个控制变量作为监控变量,仿真数据集包含了正常工况和21种不同的故障,每种状态分别包括480组训练数据和960组测试数据,在所有的过程监测测试数据中,故障均从第161组数据开始引入故障.现对几种典型的故障进行检测,即故障1(阶跃型)、故障2(阶跃型)、故障8(随机型)、故障13(慢偏移型).图4为故障1的检测结果,图5为4组故障的检测效率及所用时间柱状图,表1为 4种故障的故障检测率及所用时间的统计. 表1 4种故障的检测结果Table 1 4 the fault detection results 选取前3个变量作为主元,第4至第6个变量作为残差主元.由图4可以看出PCA-SVDD方法的检测效果要优于SVDD.这是因为SVDD方法所获得的支持向量的个数少,支持向量所占的比重小,不能进行很好地分类;PCA-SVDD方 法通过主元提取获得更多的支持向量,支持向量所占的比重增大,这样可以更好地分类.利用PCA-SVDD的故障检测方法可以有效地提取数据的特征,获得维数简约的样本数据,在计算时间上也比SVDD方法的用时短.从表1可以看出:PCA-SVDD方法的两项指标的检测效果明显优于SVDD方法. 图4 故障1检测结果Fig.4 The results of fault detection 1 图5 故障检测率及所用时间Fig.5 The fault detection rate and time histograms used 针对传统SVDD算法对大样本集操作时的检测时间长、检测效率低等不足,提出了一种PCA和SVDD结合的故障检测方法,该方法有两个优势:一是利用SVDD算法对主元空间得分及残差空间得分进行检测,与传统的SVDD算法对所有数据都进行检测相比,降低了检测时间;二是,相较于传统的SVDD算法,PCA-SVDD将PCA有效提取数据特征的优势与SVDD可以有效地处理非高斯非线性数据的优势相结合,在突出有效特征信息的同时又获得更多的支持向量,使支持向量所占的比重增大,有利于SVDD更好地进行分类,避免了漏检率,从而提高了故障检测率. : [1] 赵晓君,郑倩.基于PCA-KNN聚类的通用在线故障诊断算法设计[J].计算机测量与控制,2015,23(8):2762-2765. [2] KARIMI H R,ZAPATEIRO M,LUO N.A Linear Matrix Inequality Approach to Robust Fault Detection Filter Design of Linear Systems with Mixed Time-Varying Delays and Non-linear Perturbations[J].Journalof The Franklin Institute.2010,347(6):957-973. [3] 孙蓉,刘胜,张玉芳.基于参数估计的一类非线性系统故障诊断算法[J].控制与决策,2014,29(3):506-510. [4] 王国刚,史泽林,刘云鹏.多分辨率迭代切距离及其在目标识别中的应用[J].红外与激光工程,2012,41(5):1369-1373. [5] 周东华,李钢,李元.数据驱动的工业过程故障诊断技术——基于主元分析与偏最小二乘的方法[M].北京:科学出版社,2011:1-14. [6] 郭金玉,赵璐璐,李元.基于统计特征的不等长间歇过程故障诊断研究[J].计算机应用研究,2014,31(1):128-130. [7] 杨正永,王昕,王振雷.一种非线性过程监控方法[J].计算机与应用化学,2013,30(10):1131-1134. [8] CHANG Y Q,LU Y S,WANG F L,et al.Sub-Stage PCA Modelling and Monitoring Method for Uneven-Length Batch Processes[J].The Canadian Journal of Chemical Engineering,2012,90(1):144-152. [9] WISE B M,RICKER N L,VELTKAMP D F,et al.A Theoretical Basis for The Use of Principal Component Models for Monitoring Multivariate Processes[J].Process Control & Quality,1990,1(1):41-51. [10] KRESTA J V,MACGREGOR J F,MARLIN T E.Multivariate Statistical Monitoring of Process Operating Performance[J].The Canadian Journal of Chemical Engineering,1991,69(1):35-47. [11] 苑天琪,胡静,文成林.T-PLS下相关系数矩阵对质量影响的研究[J].杭州电子科技大学学报,2013,33(6):120-123. [12] GE Z Q,SONG Z H.Process Monitoring Based on Independent Component Analysis-Principal Component Analysis(ICA-PCA)and Similarity Factors[J].Industrial and Engineering Chemistry Research,2007,46(7):2054-2063. [13] 徐莹,邓晓刚,钟娜.基于ICA混合模型的多工况过程故障诊断方法[J].化工学报,2016,67(9):3793-3803. [14] TAX D M J,DUIN R P W.Support Vector Data Description[J].Machine Learning,2004,54(1):45-66. [15] 谢彦红,孙呈敖,李元.基于滑动窗口SVDD的间歇过程故障监测[J].信息与控制,2015,44(5):531-537. [16] 张少捷,王振雷,钱锋.基于LTSA的FS-SVDD方法及其在化工过程监控中的应用[J].化工学报,2010,61(8):1894-1900. [17] 杨正永,王昕,王振雷.基于LTSA-Greedy-SVDD的过程监控[J].华东理工大学学报(自然科学版),2014,40(3):342-348.2 基于PCA的SVDD故障检测
2.1 主元分析(PCA)

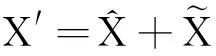

2.2 PCA-SVDD建模及检测

3 仿真实验
3.1 数值仿真


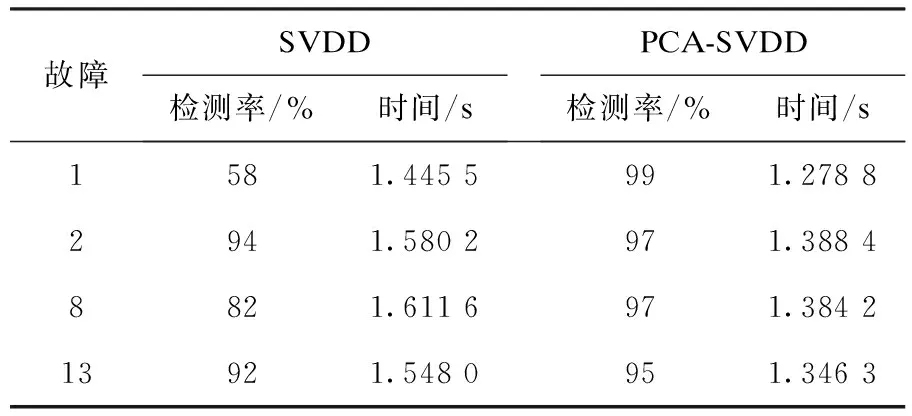
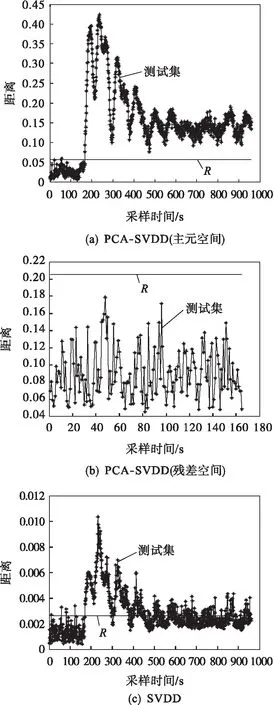
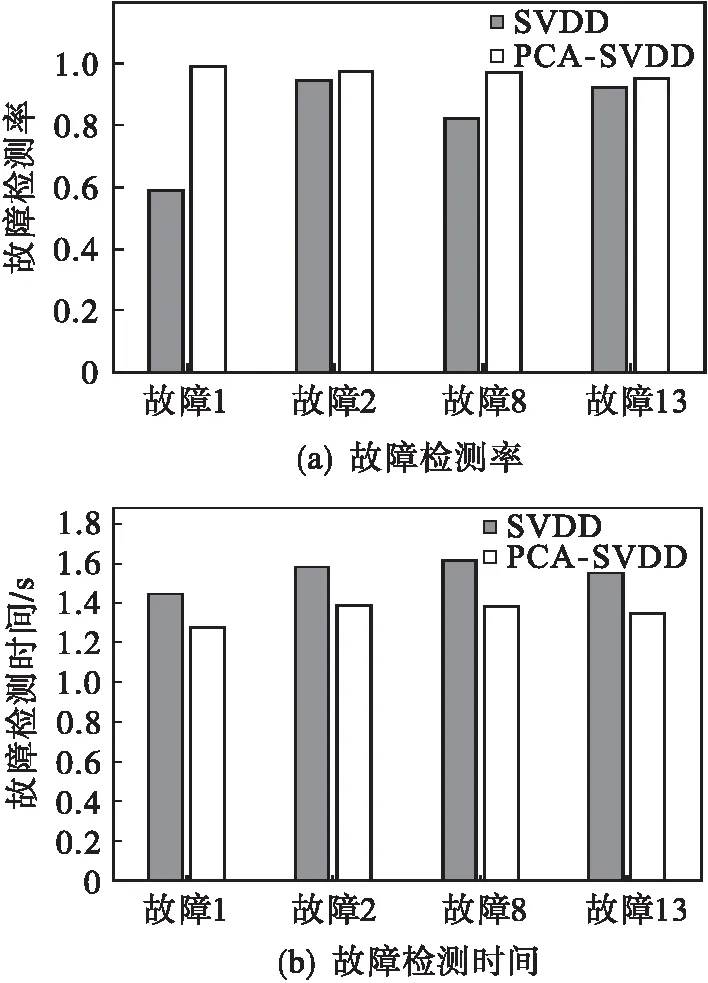
3.2 TE过程仿真
4 结 论
