一种考虑恢复的盐岩流变-损伤本构模型
2018-05-30王贵君蔡晟鑫刘熙媛
王贵君,蔡晟鑫,刘熙媛,李 东,张 岭
(河北工业大学 土木与交通学院,天津 300401)
盐岩具有结构致密、渗透性低、流变性强、可恢复等特性,适合用于建造石油、天然气储库、高放射性核废料处置库[1]。盐岩油气储库已在欧美国家得到了广泛应用,我国也加大了对盐岩储库的研究与建设的投入。
在盐岩储库设计时,采用考虑恢复的本构模型与不考虑恢复的模型相比,可以降低盐穴最小存储压力,增大储库工作压力区间,进而提高盐穴储库存储油气的能力,降低造价。因此,开展盐岩流变-损伤恢复特性的研究具有重要科学意义和工程价值。
针对盐岩的恢复特性,人们已经做了一些机理方面的研究。HOUBEN et al[2]提出将盐岩裂隙愈合机理分为3种类型:a.盐岩受压缩弹性变形或者塑性流动,使裂隙闭合;b.盐岩晶粒表面能降低,引起介质扩散或化学愈合,使裂隙缩小甚至完全弥合,减小盐岩渗透性,提高盐岩强度;c.盐岩的再结晶作用使得外部热能驱动晶粒界面上的物质迁移至裂隙表面,逐步增大裂隙接触面积,使裂隙最终完全愈合。PFEIFLE et al[3]在WIPP盐岩三轴流变试验中通过监测损伤发展和岩样渗透系数变化研究盐岩的恢复,采用一阶动力方程描述恢复规律。梁卫国等[4]对无水芒硝盐岩试件进行了完全剪切试验,发现高温条件对盐岩内摩擦角恢复效果明显,对内聚力恢复作用不大。陈结等[5]通过对盐岩试样进行不完全剪切试验,发现盐岩的损伤特征对剪切方向敏感度较高。姜德义等[6]通过对损伤盐岩进行自恢复试验,发现盐岩损伤恢复并不是简单的力学性质的增强,而是综合性质的改善。
在试验研究基础上,不少学者提出了适于盐岩的本构模型。CHAN et al[7]在MUNSON et al[8]提出的MD模型的基础上,提出了一种可以同时考虑位错流变、剪切损伤、张拉损伤和损伤恢复的多机制耦合模型——MDCF(multimechanism deformation coupled fracture)模型。DEVRIES et al[9-11]在有限元法中采用损伤势理论和MDCF模型,求得不产生扩容条件下的盐岩储库最小运行压力,研究了增大运行压力后的损伤恢复发展过程;应用于盐岩储库后成功降低了储库的最小运行压力,提高了储库存储能力。HOU et al[12]和LUX et al[13]运用连续介质力学,在Lubby2流变模型基础上,提出了一个可以考虑损伤恢复的流变模型,并将其应用于放射性核废料处置库工程中。然而,由于参数过多且确定参数的过程复杂,MDCF模型和Hou/Lux模型很难得到推广应用。笔者在Cater模型基础上提出了一种可以定量描述盐岩损伤发展的流变-损伤模型,并通过试验验证了该模型的正确性[14](以下简称此模型为“原模型”)。
本文以流变试验数据为基础,在原模型基础上,考虑盐岩的流变-损伤恢复,建立一个同时考虑流变-损伤、损伤破坏、恢复的盐岩流变-损伤模型,分析在不同卸载状态下盐岩流变-损伤恢复的规律,并分析盐岩流变-损伤和恢复的影响因素。
1 考虑恢复的流变-损伤本构模型
由基本原件组合而成的流变模型可以很好描述岩石的过渡、稳态流变阶段,但无法描述加速流变阶段。解决的办法可以大致分为两类:一种是按照Lemaitre的应变等效原理,将理论流变模型中的表观应力(Cauchy应力)替换为有效应力,材料性能在有效应力作用下随损伤变量的增大而不断劣化,采用适当的损伤演化方程,就可以描述岩石的加速流变阶段;另一种是在总流变变形中添加一项由应力应变状态控制、由损伤引起的流变(流变率),从而获得加速流变阶段。
依照唯象理论的思路,在原模型中增加一项恢复流变,考虑恢复的流变-损伤模型扩展为
ε=εt+εs+εd+εh.
(1)
式中:ε为总流变变形;εt为过渡流变分量;εs为稳态流变分量;εd为由损伤引起的流变分量;εh为由恢复作用引起的流变分量。

(2)
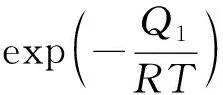
(3)

(4)

(5)
σh=-Δσi,
(6)

(7)
参照文献[14],仍然采用“损伤增速界限”的概念。考虑由卸载引起的损伤恢复,损伤演化方程变为
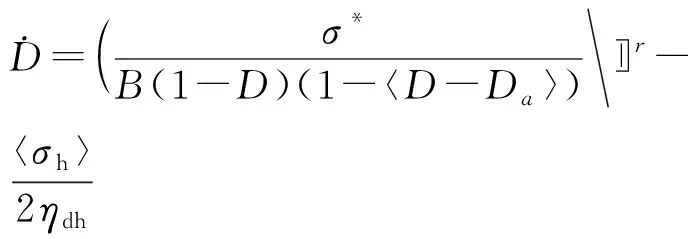
(8)

(9)
σm=(σ1+σ2+σ3)/3 .
(10)
式中:G,Gh,Gdh分别为弹性、流变和损伤恢复剪切模量;η,ηh,ηdh分别为黏滞系数、流变黏滞系数和损伤恢复黏滞系数;A1,A2,n,B,r为材料参数;Q1,Q2为材料的激活能;R为气体热力学常数,T为绝对温度;D为损伤变量,0 如果盐岩始终处于加载或恒载状态,没有卸载,σh为0,本模型退化为流变-损伤模型。 DEVRIES et al对取自美国海湾2号井(Bay Gas Well No.2,McIntosh Dome,Mobile,Alabama)盐岩试样开展了有卸载过程的三轴压缩流变试验,得到了3个盐岩试样的应变-时间变化曲线。采用MDCF模型对试验数据进行拟合分析,得到的拟合曲线如图1所示[9]。图1只给出了盐岩加载阶段流变变形的拟合曲线,没有给出卸载阶段流变恢复的拟合结果。 图1 MDCF模型计算流变曲线与试验数据的比较[9]Fig.1 Comparison between MDCF calculation and the experimental results[9] 作为对比,按照本文模型式(1)-式(10),采用最小二乘法对DEVRIES et al的试验数据进行拟合分析,得到的拟合曲线如图2中实线所示。可以看出,我们的模型可以很好地描述盐岩流变和恢复过程。拟合模型材料参数如表1所示。 图2 试验数据[9]与本模型拟合结果对比Fig.2 Comparison between model predictions and experimental results[9] 由表1可知,尽管3个试样所受荷载、历时与流变变形大小均不同,表征稳态流变及损伤恢复的参数离散性并不大,而表征弹性、过渡流变和损伤演化的参数离散性较大。产生这种现象的原因是:试样个体差异以及试验过程中产生的误差;试件从深部地层取出后产生应力卸除效应,而在稳态流变-损伤和恢复阶段已经消除了这种效应。作者在盐岩流变-损伤-破坏试验中也发现过这种效应[15]。 表1 拟合参数Table 1 Regression parameters 根据本文模型及实验拟合参数,得到上述3个盐岩试样的损伤发展曲线,如图3所示。 在试验的第二阶段即卸载段,盐岩产生了由卸载引起的流变-损伤恢复。从流变曲线(图2)和损伤曲线(图3)可以看出,盐岩流变-损伤恢复也具有明显的“过渡”(“衰减”)特点,流变恢复和损伤恢复速率逐渐减小,直至本级卸载效应消失,流变变形和损伤发展速率又变为正值,流变曲线与损伤曲线均呈上凹形状。这个阶段的流变-损伤“过渡”恢复现象消失后,试件流变变形速率和损伤发展速率比恢复前的速率均有所降低。显然,3个试样的损伤均未达到损伤增速界限,因此,损伤变量和流变变形发展缓慢。 图3 损伤变量D全程变化曲线Fig.3 Curves of damage evolution D vs. time 需要说明的是,在加载阶段,3个试件承受的应力差(相当于流变-损伤等效应力)Δσ依次分别为13.79,17.24,20.68 MPa;稳态流变速率分别为4.06×10-4,1.29×10-3,5.04×10-3d-1;稳态损伤速率分别为1.27×10-4,9.70×10-4,1.42×10-3d-1.在卸载阶段,3个试件等效应力卸载量分别为3.45,3.45,6.89 MPa;试样3的卸载量为试样1和试样2的2倍,试样3的损伤恢复程度比试样1和试样2的大,导致图3中曲线2在第二阶段位于曲线3上方。3个试样第二阶段稳态损伤速率分别为8.93×10-5,8.47×10-4,5.19×10-4d-1. 在第二阶段,试样2和试样3承受的等效应力相同,均为13.79 MPa;卸载效应消失后的稳态损伤速率值接近,但因加载和流变历史不同,损伤变量绝对值不同。 本节根据试样3的试验条件,研究本模型在卸载条件下恢复等效应力σh、参数r、B和n对盐岩流变-损伤及其恢复的影响。 在三轴压缩试验中,轴向荷载的卸载大小对盐岩试件的流变-损伤恢复是控制性的,即σh与Gdh的比值控制盐岩损伤恢复大小。卸载(即恢复等效应力大于零)后,损伤变量演化速率快速降低,其影响随时间逐渐减弱,最终消失,恢复量呈现衰减的特征,恢复后的损伤演化速率较恢复前有所降低。 如图4所示,试验时间t=12 d时发生轴向卸载;当σh= 6,8,10 MPa时,损伤恢复极限值分别为0.010,0.013,0.017;损伤恢复时间等于损伤恢复延迟时间(ηdh/Gdh=1.25 d)时,损伤恢复达到最终值的63%. 这里的损伤恢复延迟时间仅影响损伤恢复的快慢程度,不影响其恢复大小。 图4 损伤变量D与时间t及恢复等效应力σh关系曲线Fig.4 Damage evolution D vs. time t with different equivalent recovery stresses 参数r对盐岩损伤演化速率影响较大,如图5所示。三轴压缩试验中轴向卸载(t=12 d)导致盐岩试样损伤演化速率显著降低,损伤恢复(损伤变量的减小)量随r值的增加而增加。此外,盐岩在稳态流变阶段的损伤演化速率随r值的增大而减小。 需要注意的是,取r=4.2,荷载持续到第18天时,损伤变量超过损伤增速界限Da(Da=0.12);之后损伤变量迅速增大,到第33天,损伤演化速率已接近无穷大,试件将发生破坏(图5). 图5 损伤变量D与时间t及参数r关系曲线Fig.5 Damage evolution D vs. time t with different values of r 参数B对损伤变量的影响与参数r的影响类似(图6).到试验的第33天为止,当B=125,135 MPa时,损伤发展极为缓慢,损伤变量值均小于0.04.然而,当B=105 MPa时,在第33天,损伤变量已达0.19,超过损伤增速界限,试样将发生破坏。 图6 损伤变量D与时间t及参数B关系曲线Fig.6 Damage evolution D vs. time t with different values of B 参数n为稳态和损伤流变速率的应力指数,对盐岩的流变速率影响极大。在其他模型参数恒定的条件下,过渡阶段和恢复阶段盐岩流变速率随参数n的增大而增大;n分别为6.2,5.8,5.4时对应的稳态流变速率分别为0.030,0.009,0.003 d-1;而恢复后再达到稳态流变阶段的时间与参数n无关,本组试验达到稳态流变的时间约为7 d左右,如图7所示。 图7 总蠕变率与时间t及参数n关系曲线Fig.7 Curves of creep rate vs. time t with different values of n 1) 在过渡流变和稳态流变阶段,盐岩流变和损伤速率均较小,损伤变量值也很小。 2) 在三轴压缩试验中,保持围压不变,减小轴向压力,使盐岩试件的流变和损伤产生恢复。 3) 盐岩的流变-损伤恢复具有明显的“过渡”特点。流变变形恢复和损伤恢复效应是一个衰减过程,恢复速率逐渐减小,直至本级卸载效应消失,流变变形和损伤发展速率又变为正值。达稳态后试件流变变形速率和损伤发展速率比恢复前的速率均有所降低。 本文提出的盐岩流变-损伤-恢复模型不但继承了原模型描述盐岩流变-损伤-破坏全过程的特性,也能真实地反映卸载后盐岩流变-损伤恢复。表征盐岩稳态流变-损伤和恢复的模型参数离散性不大。 : [1] 杨春和,白世伟,吴益民.应力水平及加载路径对盐岩时效的影响[J].岩石力学与工程学报,2000,19(3):270-275. YANG C H,BAI S W,WU Y M.Effect of stress level and loading path on time dependent properties of salt rock[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):270-275. [2] HOUBEN M E,HOVE A T,PEACH C J,et al.Crack healing in rock salt via diffusion in adsorbed aqueous films:microphysical modelling versus experiments[J].Physical and Chemistry of the Earth,2013,64(64):95-104. [3] PFEIFLE T W,HURTADO L D.Permeability of natural rock salt from the waste isolation pilot plant (WIPP) during damage evolution and healing[J].International Journal of Rock Mechanics and Mining Sciences,1998,35(4):637-638. [4] 梁卫国,徐素国,赵阳升.损伤盐岩高温再结晶剪切特性的试验研究[J].岩石力学与工程学报,2004,23(20):3413-3417. LIANG W G,XU S G,ZHAO Y S.Experimental study on heating recrystallization effect on shear characteristics of damaged rock salt[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(20):3413-3417. [5] 陈结,刘剑兴,姜德义,等.围压作用下盐岩应变与损伤恢复试验研究[J].岩土力学,2016,37(1):105-112. CHEN J,LIU J X,JIANG D Y,et al.An experimental study of strain and damage recovery of salt rock under confining pressures[J].Rock and Soil Mechanics,2016,37(1):105-112. [6] 姜德义,王雷,陈结,等.损伤盐岩短期自恢复特性试验研究[J].岩土工程学报,2015,37(4):594-600. JIANG D Y,WANG L,CHEN J,et al.Experimental research on properties of short-term self recovery of damaged salt rock[J].Chinese Journal of Geotechnical Engineering,2015,37(4):594-600. [7] CHAN K S,BODNER S R,MUNSON D E,et al.A constitutive model for representing coupled creep,fracture,and healing in rock salt[C]∥Proceedings of the 4th Conference on the Mechanical Behavior of Salt.Clausthal-Zellerfeld,Germany:Trans Tech Publications,1996:3553-3565. [8] MUNSON D E,DAWSON P R.Salt constitutive modeling using mechanism maps[C]∥Proceedings of the First International Conference on the Mechanical Behavior of Salt.Clausthal-Zellerfeld,Germany:Trans Tech Publications,1981:717-737. [9] DEVRIES K L,MELLEGARD K D,CALLAHAN G D.Proof-of-concept research on a salt damage criterion for cavern design:a project status report[C]∥Solution Mining Research Institute Spring 2002 Meeting.Banff,Alberta,Canada,2002. [10] DEVRIES K L,NIELAND J D,RATIGAN J L.Feasibility study for lowering the minimum gas pressure in solution-mined caverns based on geomechanical analyses of creep-induced damage and healing:Topical report RSI-0969,DE-AC26-97Fr34350[R/OL].Morgantown,West Virginia,US:Federal Technology Center Department of Energy,1998.[2016-03-05].https://www.onepetro.org/other/661. [11] DEVRIES K L,MELLEGARD K D,CALLAHAN G D.Salt damage criterion proof-of-concept research:Topical report RSI-1557,DE-FC26-00NT41026[R/OL].National Energy Technology Laboratory,Department of Energy,The United States.[2016-03-02].https://www.onepetro.org/other/3870. [12] HOU Z,LUX K H.Ein neues Stoffmodell für ductile salzgesteine mit einbeziehung von gefügschadigung und tertiarem kriechen auf der grundlage der continuum-damage-mechanik[J].Geotechnik,1998,21(3):259-263. [13] LUX K H,HOU Z.New developments in mechanical safety analysis of repositories in rock salt[C]∥Proceedings of the International Conference on Radioactive Waste Disposal,Disposal Technologies and Concepts.Germany:Springer-Verlag,2000:281-286. [14] WANG G J.A new constitutive creep-damage model for rock salt and its characteristics[J].International Journal of Rock Mechanics and Mining Science,2004,41(3):61-67. [15] WANG G J,ZHANG L,ZHANG Y W,et al.Experimental investigations of the creep-damage-rupture behaviour of rock salt[J].International Journal of Rock Mechanics and Mining Sciences,2014,66(1):181-187.2 模型的比较与验证
2.1 MDCF模型与试验数据拟合结果
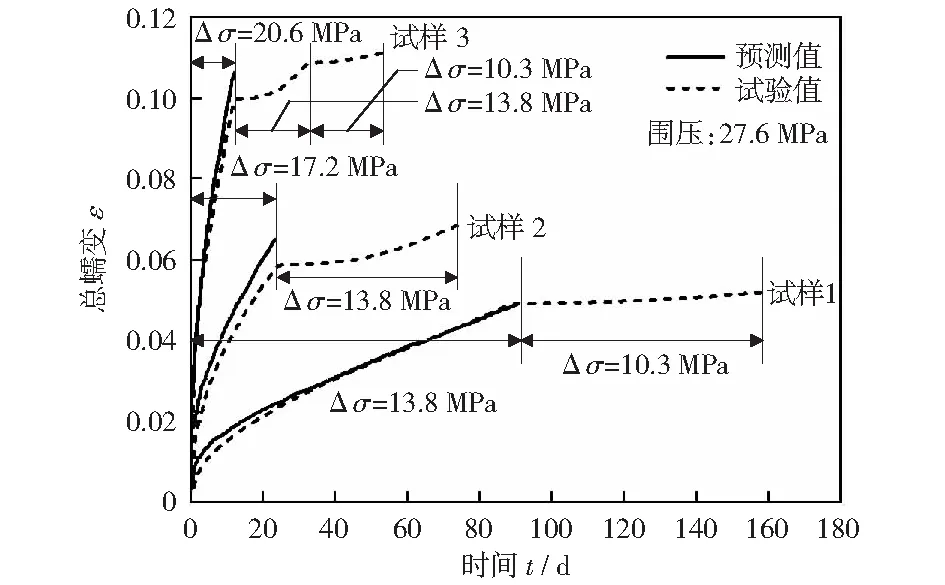
2.2 本模型的拟合结果


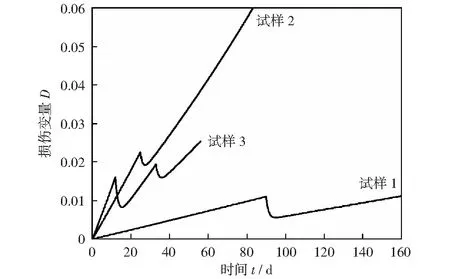
3 材料流变-损伤的影响因素分析
3.1 恢复等效应力σh和恢复延迟时间ηdh/Gdh
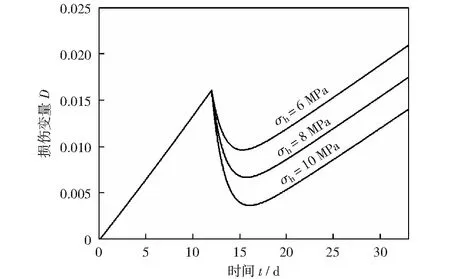
3.2 参数r和B
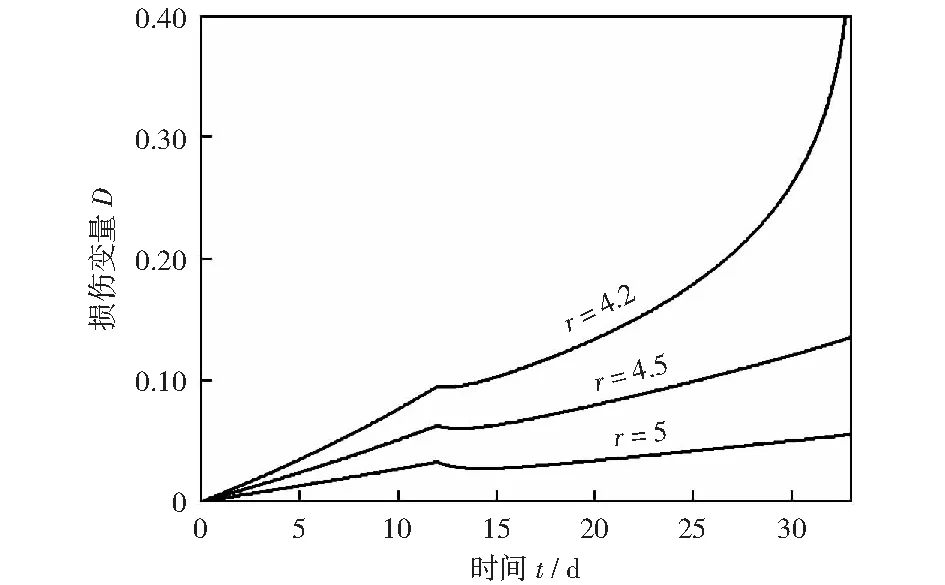

3.3 参数n

4 结论
