圆锥曲线中范围问题背后不等关系的寻找
2018-05-30江苏省锡山高级中学214174吴宝莹
江苏省锡山高级中学 (214174) 吴宝莹 季 斌
在现实世界和日常生活中,存在着两种关系,一种是不等关系,一种是等量关系,等量关系可以看作一种特殊的不等关系,等量关系只是相对的,不等关系大量存在.圆锥曲线中基本量的计算属于等量关系问题,比较简单,而求基本量或参数的范围就属于不等关系问题,比较困难.如求离心率的大小只要建立关于基本量a、b、c的齐次方程就可以求出来,而求离心率的取值范围就要寻找离心率取值范围背后的某种不等关系,再转化为关于离心率的不等关系,才能求出离心率的取值范围.后者要比前者困难得多,难就难在“所求问题背后的某种不等关系”的寻找,事实上,离心率的取值范围仅仅是表面现象,其“幕后的操纵者”是“某种不等关系”,正如物理学中的布朗运动,表面上是悬浮微粒做无规则运动,实际上是悬浮微粒被大量分子撞击所形成的,是分子在做无规则运动.因此,要解决圆锥曲线中基本量或参数的范围问题就要透过现象看本质,寻找出其“幕后的操纵者”——某种不等关系,那么怎样寻找这个“某种不等关系”呢,一般有以下几种方法:
1.利用题目本身条件寻找“不等关系”
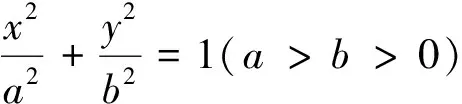
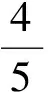
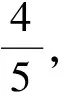
2.利用焦半径范围寻找“不等关系”
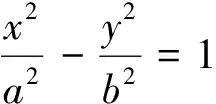
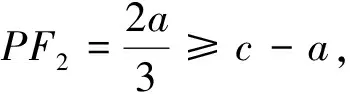
点评:因为点P在双曲线的右支上,所以点P到右焦点的距离PF2≥c-a,利用焦半径范围寻找“不等关系”.
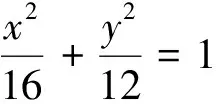
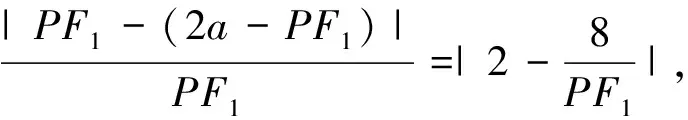
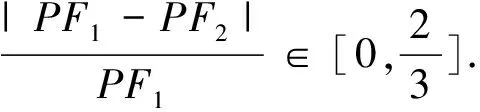
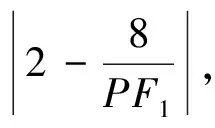
3.利用曲线上动点横坐标(纵坐标)的范围寻找“不等关系”
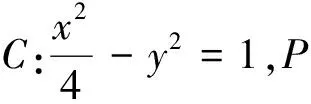
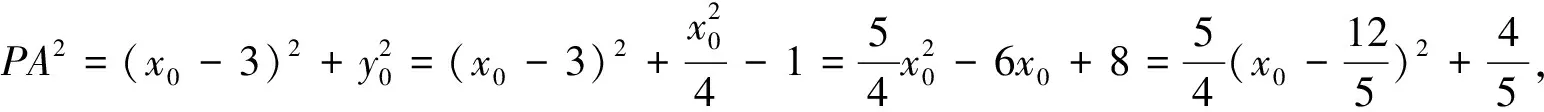
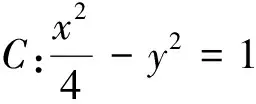
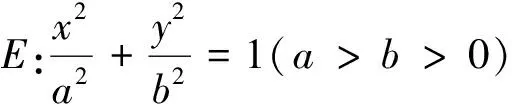
(1)求椭圆的方程;
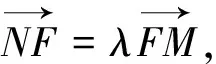
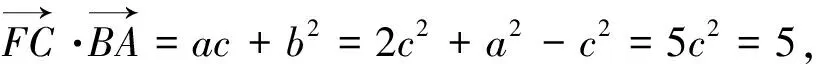
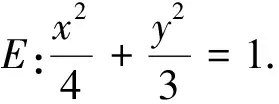
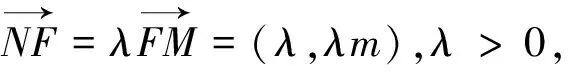
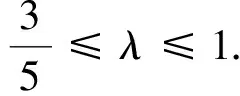
法二:连接CF并延长交椭圆于点N′,则xN′=
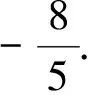
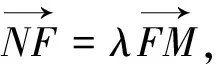
4.利用圆锥曲线基本量之间的本身大小关系寻找“不等关系”
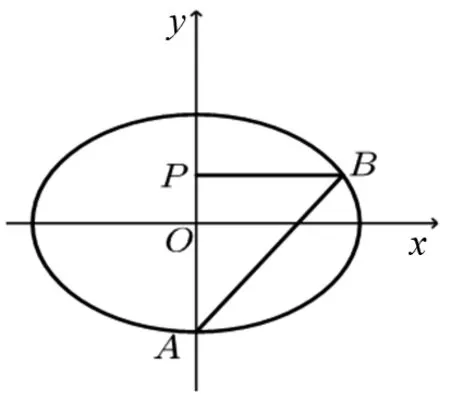
图1
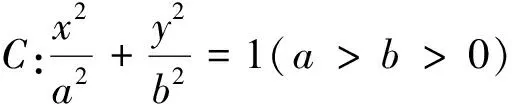
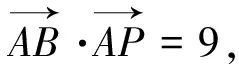
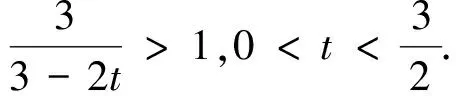
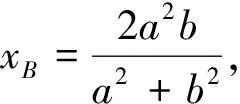
点评:利用椭圆基本量a,b之间本身的大小关系a>b寻找“不等关系”.
5.利用判别式Δ>0寻找“不等关系”
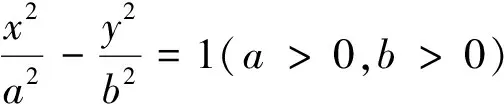
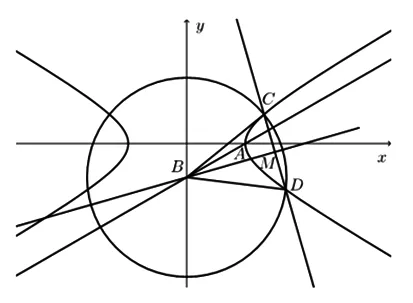
图2
(1)求双曲线的方程;
(2)直线y=kx+m(k≠0,m≠0)与该双曲线交于不同的两点C、D,且C、D两点都在以B为圆心的同一圆上,求实数m的取值范围.
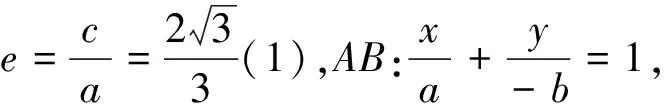
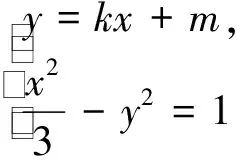
点评:直线y=kx+m(k≠0,m≠0)与该双曲线交于不同的两点,所以判别式Δ=(-6km)2-4(1-3k2)(-3m2-3)>0,得到关于m,k的不等关系m2+1>3k2(1),再由CB=DB,点B在线段CD的垂直平分线上,建立关于m,k的等量关系4m+1-3k2=0(2),联立(1)(2)就可以求出实数m的取值范围.
