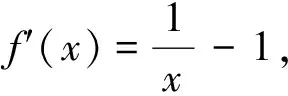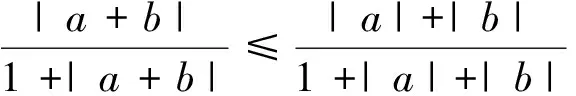例谈教材中的构造法

广东省开平市第一中学 (529300) 梅延峰

在解题时，通过对条件和结论的分析，构造辅助元素，它可以是一个图形、一个方程(组)、一个等式、一个函数、一个等价命题等，架起一座连接条件和结论的桥梁，从而使问题得以解决，这种解题的数学方法，我们称为构造法.运用构造法解题，可以使代数、三角、几何等各种数学知识互相渗透，有利于问题的解决.构造法解题是一种创造性的思维活动，构造法是依据题设的特点，用已知条件中的元素为“元件”，把已知数学关系作“支架”，构造出一种新的数学模型，沟通数学模型间的相互关系，从而转换命题.运用构造法，常使数学解题突破常规，具有简洁、明快、精巧的优点，下面以人教A版教材的例题和习题来感受一下解题中的构造法思想.

一、构造组合数

例1 在(1+x)3+(1+x)4+…+(1+x)n+2的展开式中，含x2项的系数是多少？

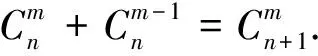
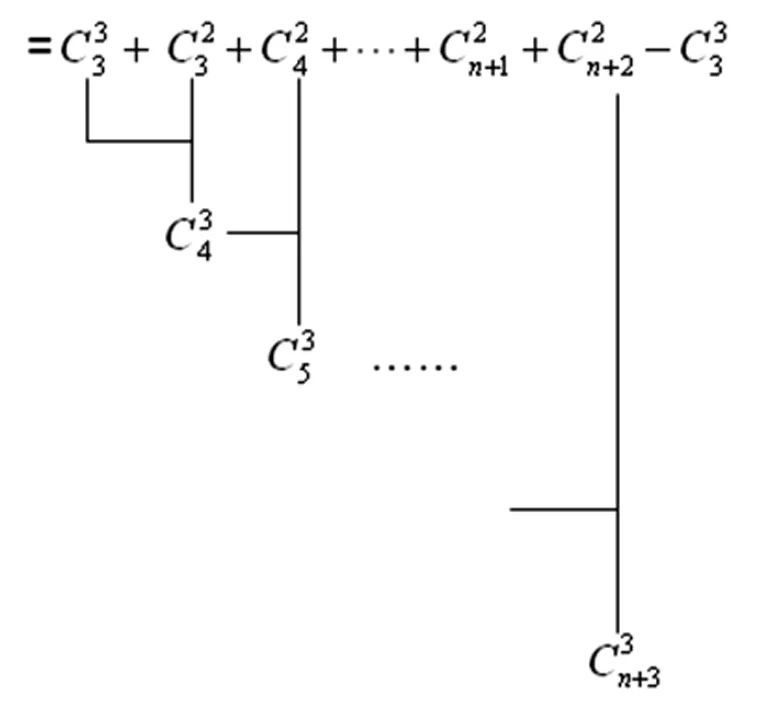
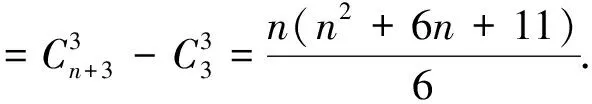
例2 已知：a≠b，求证a4+6a2b2+b4>4ab(a2+b2).

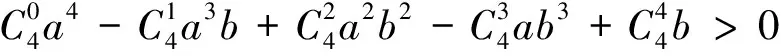
二、构造数列

例3 一个蜂巢里有1只蜜蜂，第一天，它飞出去找回了5个伙伴；第二天，6只蜜蜂飞出去，各自又找回了5个伙伴……,如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢一共有( )只蜜蜂.

解析：可构造数列a1=1，an+1=5an+an，可计算到第6天所有的蜜蜂都归巢后，蜂巢一共有a6=46656只蜜蜂.

三、构造几何图形

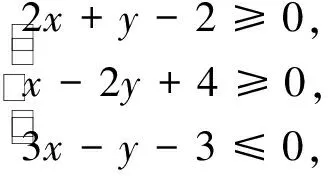
解析：可构造目标函数z=

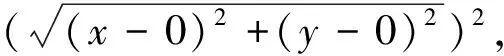
四、构造向量

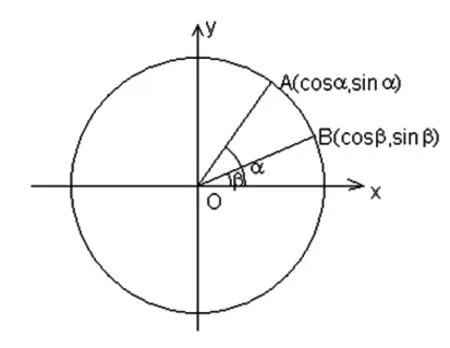
图1

例5 如图1，在直角坐标系中，以原点O为圆心，单位长度为半径的圆上有两点A(cosα,sinα),B(cosβ,sinβ),试用A、B两点的坐标表示∠AOB的余弦值.

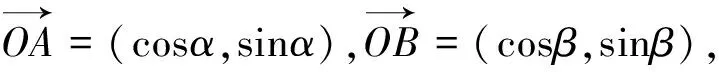
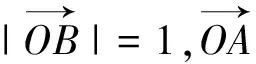
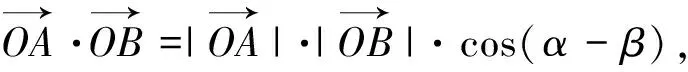
五、构造三角式

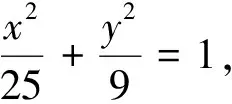
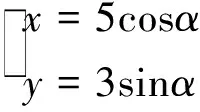
六、构造函数

例7 利用函数的单调性证明不等式lnx

辩证唯物主义认为事物是普遍联系的，在数学中不同的数学分支间也都具有这种联系性，有的显而易见，有的则较为隐蔽，数学教学的一个功能就是要向学生揭示这种关系，在这个过程中，可以使学生的知识体系得到整合，并逐渐对数学中的各种思想方法产生较为清晰的认识，对数学解题方法的拓展其实也是一种联系性的拓展，构造法是基本的数学方法，构造的对象可以是各种各样的，但要注意抓住问题的本质特征，构造出相关模型(式子)来使问题得以简化，并为问题的最终解决铺平道路.