高考数学审题思维分析

云南省施甸县第一中学 (678200) 张玉虎

高考数学试题所考查的知识覆盖面广，试题容量大，考试时间紧，因此要想取得理想的考试成绩，除必须熟练掌握高中数学基础知识和基本方法外，解题时审题思维的精准程度成为了能否快速解题的关键，尤其在难题的突破上更为重要，考生审题思维的差异性正是试题突显选拔功能的着力点，而解题方向和解题方法实质就来自题目的字里行间，审清题意就能正确把握解题方向.

一、审已知条件，挖掘隐含条件

(A)0 (B)m(C)2m(D)4m

例2 已知a、b、c都是常数，a>b,c>d，若f(x)=2017-(x-a)(x-b)的零点为c、d，则下列不等式正确的是( ).

(A)a>c>b>d(B)a>b>c>d

(C)c>d>a>d(D)c>a>b>d

分析：函数f(x)=2017-(x-a)(x-b)中含有两个隐含条件：①抛物线的开口向下；②f(a)=f(b)=2017，利用数形结合可得：c>a>b>d，故选D.

二、审问题本质，联系知识生成

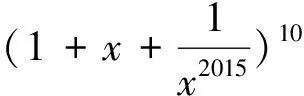
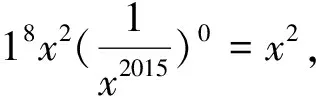
三、审结构特征，确定解决方案

例4 已知等比数列{an}的前n项和为Sn，且a3=2S2+1，a4=2S3+1，则公比q的值为( ).

(A)3 (B)-3 (C)-1 (D)1

分析：等比数列有两个基本量a1和q，已经知道两个等式可以利用方程组来求解，但解方程组繁琐，且要求计算能力高.观察式子a4=3S3+1与a3=2S2+1的结构特征，可用两式相减得：a4-a3=2a3，从而快速求得q=3，故选A.

例5 设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)<0，则使得f(x)>0成立的x的取值范围是( ).

(A)(-∞,-1)∪(0,1)

(B)(-1,0)∪(1,+∞)

(C)(-∞,-1)∪(-1,0)

(D)(0,1)∪(1,+∞)

四、审问题外延，退步探索结论

例6 正四棱锥相邻侧面所形成二面角的平面角为α，侧面与底面所成的二面角为β，则2cosα+cos2β的值等于( ).

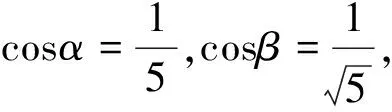
五、审结论要件，善于等价转化

(1)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立，求满足条件的最大整数M；

分析：(1)存在x1、x2∈[0,2]使得g(x1)-g(x2)≥M，可等价转化为[g(x1)-g(x2)]max≥M，进而转化为在x∈[0,2]上g(x)max-g(x)min≥M.

六.审解题细节，提升过程准度

例9 已知函数f(x)=(x2-2x)ex，则f(x)在其定义域R上的最值情况为( ).

(A)既有最大值，又有最小值；

(B)既无最大值，又无最小值；

(C)只有最大值，没有最小值；

(D)只有最小值，没有最大值.

例10 已知函数f(x)=|lgx|，若0

(C)(3,+∞) (D)[3,+∞)

审题过程既是一种思维方法，更是一种思维品质，学生平时审题积淀的思维模式，不仅刻画着考场上学生解题能力的差异，还反映着学生数学核心素养的不同.通过对高考数学审题思维的分析，有效地理清审题的方向，精准把握题意，才能快速找到解题突破口，在难题与繁题中展现出优良的思维品质，赢取高考数学试题选拔性功能的主动权.