基于轴心轨迹形态的转子裂纹故障分析
2018-05-29向玲,张悦
向 玲, 张 悦
(华北电力大学 机械工程系,河北保定 071003)
在转子系统中,裂纹是一种比较典型的故障。由于运转疲劳或初始加工中存在缺陷,导致转子在运行过程中产生裂纹,转轴刚度降低,稳定性下降,横向振动加剧,对转子的正常运转产生较大影响,甚至会发生严重事故。因此,检测裂纹对保证生产具有极其重要的意义。裂纹动力学特性分析是故障研究的理论基础[1]。
近年来,国内外学者对基于裂纹故障的转子进行了一系列研究。宋光雄等[2]归纳了发生裂纹的主要原因,总结了其故障特征和变化趋势,并提出了裂纹故障的诊断依据。Guo等[3]对呼吸裂纹转子的动力学特性进行了分析,验证了基于EMD裂纹检测方法的可靠性。于涛等[4]在考虑剪力因素的影响下建立了裂纹转子的有限元模型,分析得到了双裂纹转子在不同转速区和不同裂纹位置的系统响应。唐玉生[5]根据有限元方法建立了基础-轴承-转子系统的有限元模型,对简单转子系统的裂纹和裂纹-碰摩耦合故障特征进行了分析。邹剑等[6]基于传递矩阵和局部柔度理论,建立了单一开裂纹转子的有限元模型,分析了裂纹大小和位置对系统响应的影响。Ferjaoui等[7]在考虑轴承油膜力的基础上建立了柔性裂纹转子-轴承系统模型,研究了临界转速附近裂纹深度对系统响应的影响,并利用分岔图和庞加莱截面图分析了裂纹对临界转速的影响。向玲等[8]在考虑裂纹轴时变刚度、碰摩力以及油膜力的情况下建立了裂纹-碰摩双故障模型,多角度分析了转子的非线性动力学特性。陈铁锋[9]分析了单裂纹和双裂纹转子在油膜支承下的动力学特性。Al-shudeifat等[10]将有限元方法运用到裂纹刚度矩阵中,构造了新的裂纹开闭函数,并对亚临界和临界的系统响应进行了分析。刘政等[11]基于中性轴法确定了裂纹的开闭状态,并分析了在过临界转速下以及加速瞬态过程中转子的系统响应和稳定性。朱厚军等[12]基于Jeffcott转子系统,选取合理的裂纹开闭模型,对其次临界和超临界转速区的动力学响应进行了分析。
从频谱和动力学特征角度对转子裂纹故障进行分析的研究较多,基于轴心轨迹分析裂纹故障的文献较少。笔者基于裂纹转子动力学模型,在考虑裂纹转子时变刚度的情况下对转子系统1/3和1/2临界转速附近的轴心轨迹变化进行了分析。
1 含裂纹故障的Jeffcott转子系统
具有水平刚性支承的Jeffcott裂纹转子模型如图1所示。转轴两端均为刚性支承,圆盘位于转轴中心处,一横向弓形裂纹位于圆盘根部。

图1 含横向裂纹的Jeffcott转子示意图
Fig.1 Schematic diagram of a Jeffcott rotor system with transverse crack
1.1 裂纹转子开闭模型
图2为裂纹的截面图,其中xoy为转子系统中的固定坐标系,ξo′η为转动坐标系,o′为转轴中心,o′ξ轴与裂纹扩展方向相同,在转子运动过程中不考虑扭转振动,仅考虑弯曲振动。笔者采用的转子模型重力远大于不平衡力,故裂纹模型为开闭裂纹,其中裂纹张开与闭合程度随重力和不平衡力的合力变化而改变。图2中α表示裂纹角的一半,θ和φ分别表示为:
θ=ωt+φ0
(1)
φ=θ+β-Ψ
(2)
式中:θ为自转角;ω为转轴的自转角速度;t为转动时间;φ0为转轴初始相位角;β为偏心与裂纹方向之间的夹角;Ψ为转轴的涡动角;φ为转轴的转涡差角。
裂纹开闭模型为非线性,此模型建立在Gasch的开闭模型基础上,并将非线性涡动因素考虑在内[13-14]:
(3)
式中:f(φ)为裂纹的开闭函数。
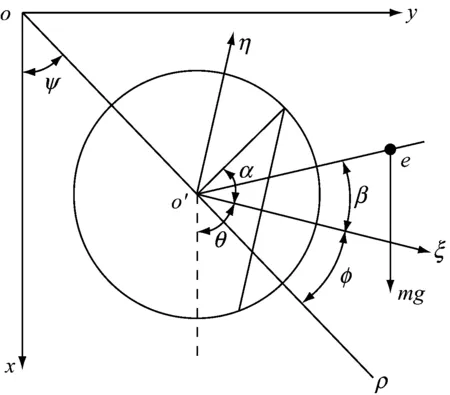
图2 裂纹截面示意图
1.2 裂纹转子刚度模型
转轴的两端为对称支承,x向与y向的支承刚度相同,不考虑耦合刚度。裂纹会改变转子的刚度,在转轴转动的过程中裂纹横截面受到的应力大小及方向时刻发生变化,变化后的刚度矩阵为K。综合考虑裂纹的大小和方向,忽略o′η轴方向的刚度变化,即
ΔK=ΔKξ
(4)
式中:ΔKξ为o′ξ轴方向的刚度矩阵变化量;ΔK为刚度矩阵的变化量。
考虑转轴的裂纹类型为呼吸裂纹,其变化后的刚度矩阵可表示为:
(5)
式中:k为无裂纹的转子刚度;Δk为有裂纹的转子刚度变化量[15]。
将转动坐标系ξo′η转化为固定坐标系xoy:
kxx=k-f(φ)Δkcos2(φ+Ψ)
(6)
kxy=kyx=-f(φ)Δkcos(φ+Ψ)sin(φ+Ψ)
(7)
kyy=k-f(φ)Δksin2(φ+Ψ)
(8)
2 裂纹转子系统运动微分方程
2.1 裂纹转子系统运动微分方程的建立
假设转轴中央圆盘处的径向位移分别为x和y,不考虑陀螺力矩和扭转振动,仅考虑转轴的弯曲振动,忽略裂纹对转子系统阻尼和质量的影响。根据Lagrange方程将两端支承连线的中心视为零势能点,则裂纹转子系统的运动微分方程为:
(9)
式中:m为圆盘质量;c为圆盘阻尼系数;e为圆盘偏心量。
2.2 裂纹转子系统运动微分方程的求解
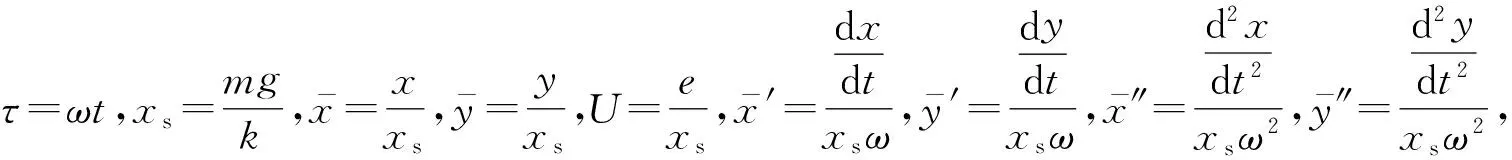
(10)
(11)
(12)
3 数值仿真与分析
3.1 参数设定
采用4阶龙格-库塔法对无量纲化后的非线性方程组进行分析求解,系统的参数如表1所示。为消除瞬态响应的影响,选用100个周期后的计算结果进行仿真,得到裂纹转子的分岔图、轴心轨迹图、庞加莱截面图、时域波形图和频谱图。

表1 系统参数
3.2 转速对系统响应的影响
以转速比为分岔参数,系统响应的分岔图如图3所示。裂纹转子刚度的变化比K1=0.1,无量纲偏心量U=0.29,转子的阻尼比ξ=0.05,其他相关参数如表1所示。考虑系统瞬态响应的影响,仿真过程从第100个周期开始,计算区间为150个周期。在转速比小于1.5时,系统未发生分岔,一直处于单周期运动状态。在次临界转速区,转子系统出现次谐波共振现象。由图3可以看出,当转速比为1/n(n=1,2,3…)时,系统出现共振现象,即曲线在相应点处出现多个峰值。
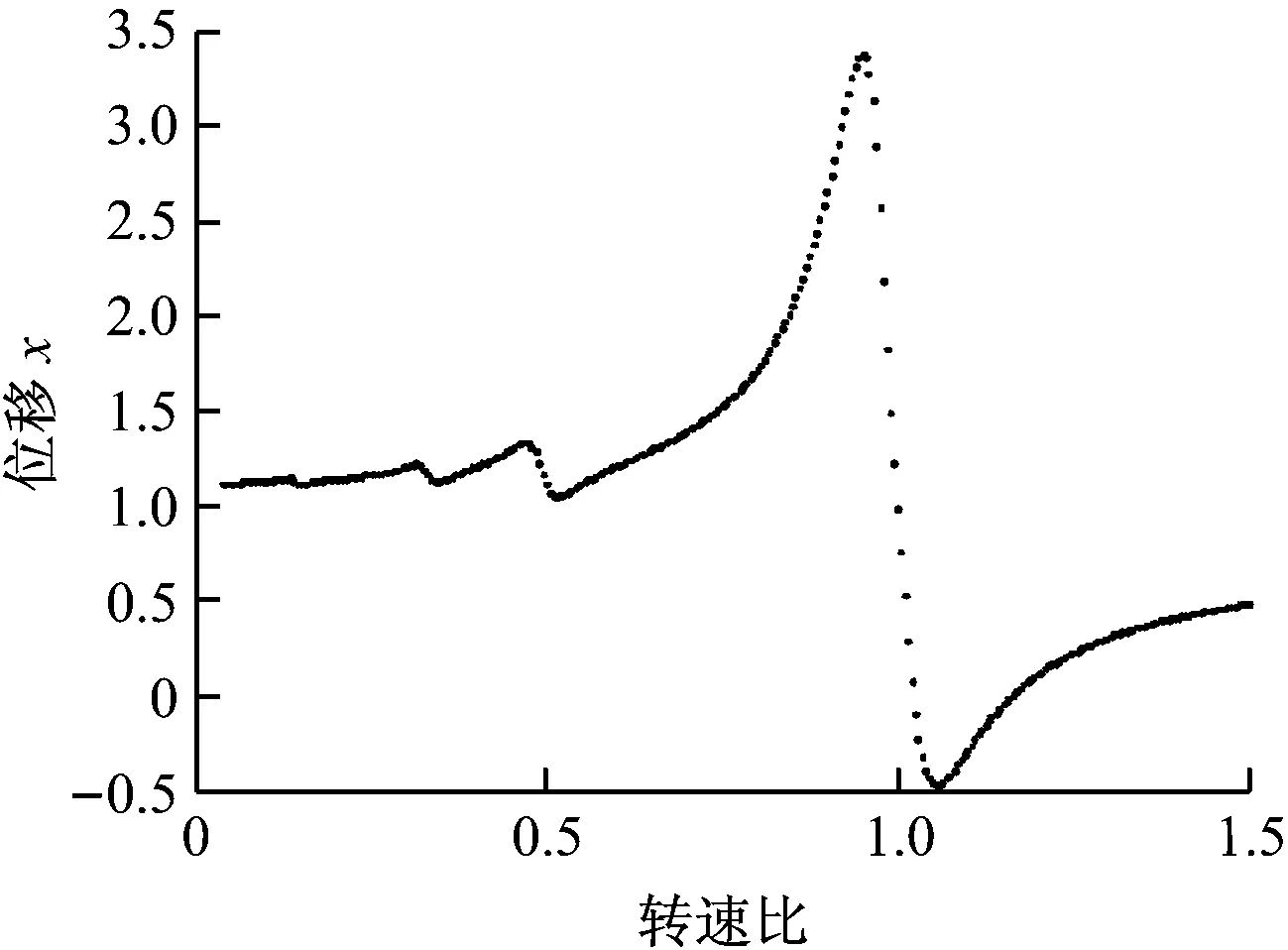
图3 系统分岔图
3.3 1/3临界转速附近的系统响应分析
在转子系统中,裂纹会影响转子刚度,进而影响系统响应。通过对比有无裂纹转子的轴心轨迹形态变化,可得出裂纹对系统响应的影响,进而通过轴心轨迹的形态特征判断是否发生裂纹故障。设定参数为β=0,U=0.29。图4为无裂纹转子系统在1/3临界转速附近的轴心轨迹图,即K1=0。当刚度变化比K1=0.1时,裂纹转子系统在1/3临界转速附近的轴心轨迹图和庞加莱截面图如图5所示。
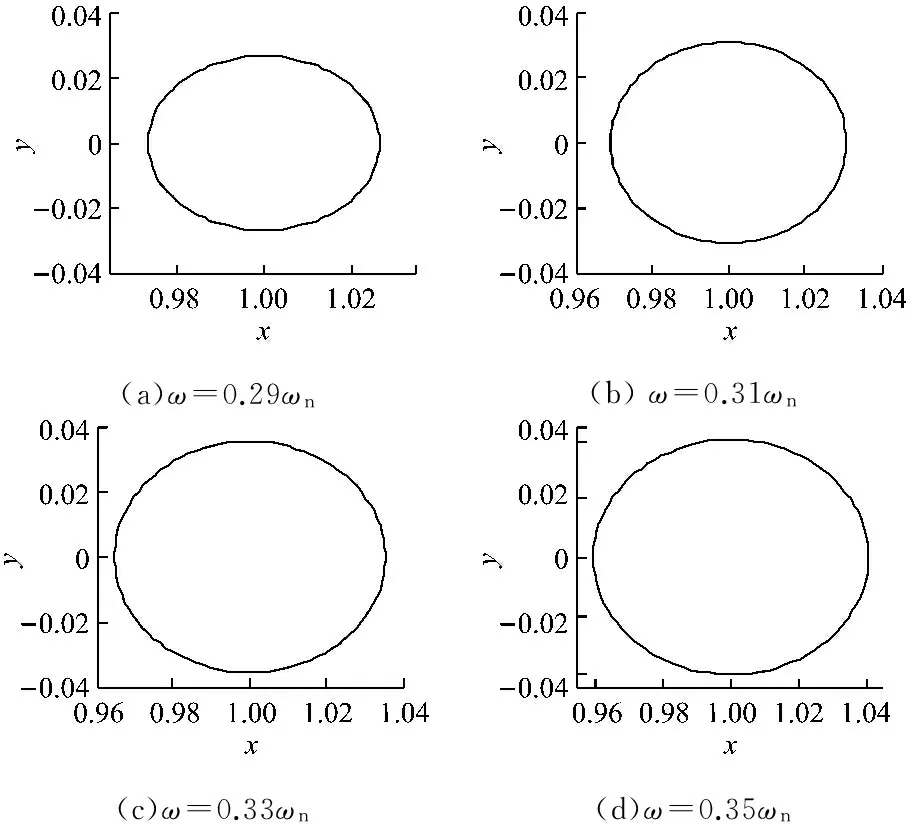
(a)ω=0.29ωn(b)ω=0.31ωn(c)ω=0.33ωn(d)ω=0.35ωn
图4 1/3临界转速区无裂纹转子的轴心轨迹
Fig.4 Axis orbits of the uncracked rotor around 1/3 subcritical speed
在1/3临界转速附近,系统响应有规律地变化,转子的轴心轨迹形态也随转速的变化而改变。由图4可知,在1/3临界转速附近,转子的轴心轨迹始终为规则圆环状,但在不同转速下,圆环的大小不同。由图5可知,在1/3临界转速附近,刚度变化比K1=0.1的裂纹转子系统轴心轨迹存在2个向内凹陷的圆环,内环的形状和偏置方向均随转速的变化而改变,且在转速的变化区间内偏置方向的变化角度约为π/2。对比分析图4和图5中轴心轨迹形态可知,与利用频谱分析的传统方法相比,通过分析系统1/3临界转速附近的轴心轨迹形态变化来判断是否存在裂纹故障更加简便、清晰。
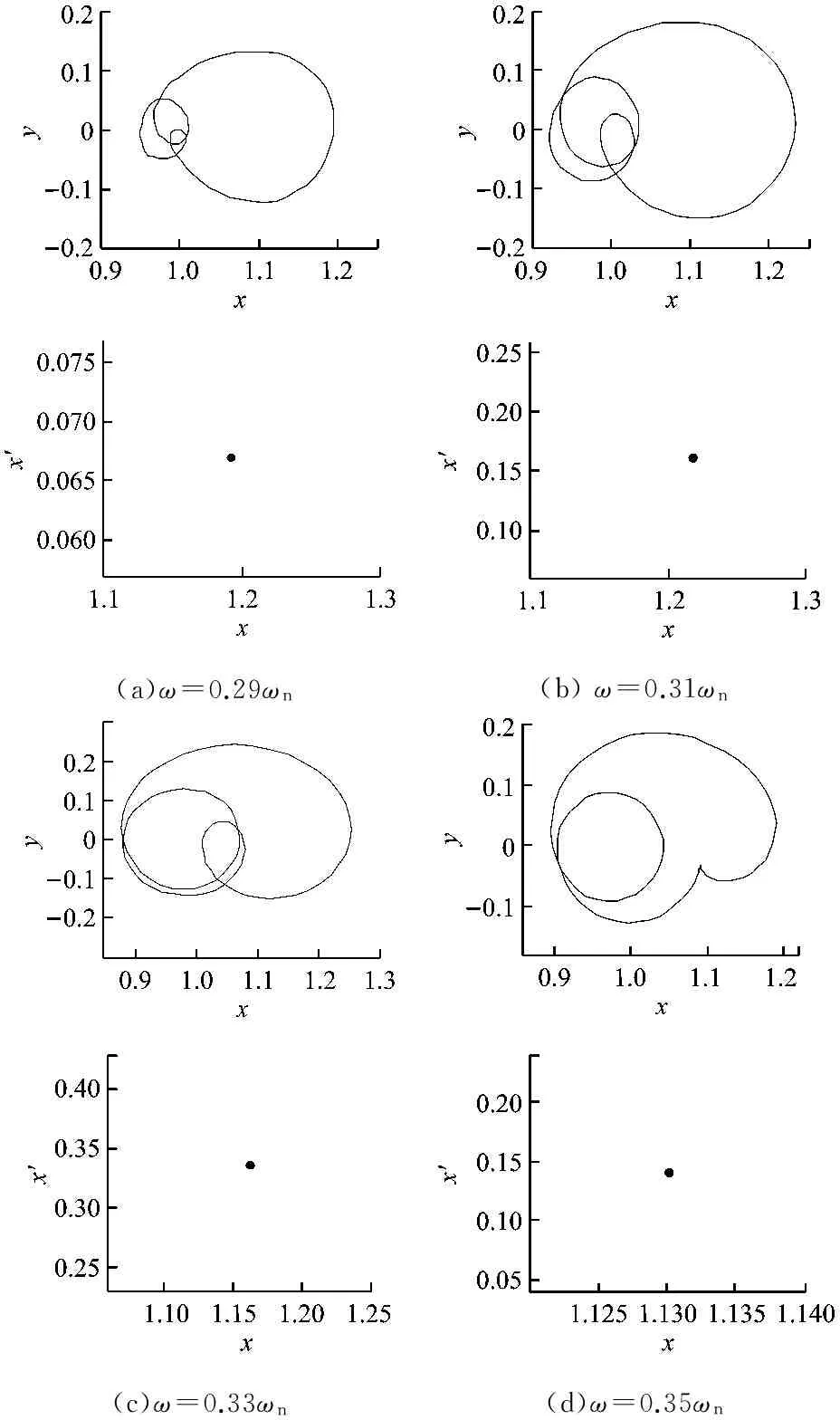
(a)ω=0.29ωn(b)ω=0.31ωn(c)ω=0.33ωn(d)ω=0.35ωn
图5 1/3临界转速区的轴心轨迹和庞加莱截面图
Fig.5 Axis orbits and poincaré maps around 1/3 subcritical speed
由图5的庞加莱截面图可知,始终仅存在1个相点,即此时裂纹转子系统的运动一直为单周期运动。
在相同的参数下,裂纹转子系统在相应转速下的时域波形图和频谱图如图6所示。其中,频谱图中f是指系统响应包含的频率成分,fr是指系统响应的基频成分,f/fr表示系统响应频率的无量纲数。系统响应中存在次谐波共振现象。由图6可知,系统在1/3临界转速处出现共振。在1/3临界转速附近,时域波形均为周期信号,随着转速的提高,振动幅值先增大后减小,且在1/3临界转速处振动幅度最大。图3中转速比为1/3处出现一个峰值。频谱图中出现1X、2X、3X、4X等谐波频率成分,其中谐波成分1X、2X、3X具有较大的幅值,且随转速的提高,各谐波成分的幅值变化趋势为先增大后减小,当达到1/3临界转速时,各谐波频率成分的幅值达到最大。

(a)ω=0.29ωn(b)ω=0.31ωn(c)ω=0.33ωn(d)ω=0.35ωn
图6 1/3临界转速区的时域波形和频谱图
Fig.6 Time series and frequency spectra around 1/3 subcritical speed
3.4 1/2临界转速附近的系统响应分析
设定参数为β=0,U=0.29。图7为无裂纹转子系统在1/2临界转速附近的轴心轨迹。图8和图9分别为刚度变化比K=0.1时裂纹转子系统在1/2临界转速附近的轴心轨迹、庞加莱截面图以及时域波形图、频谱图。
无裂纹转子系统在1/2临界转速附近的轴心轨迹始终为圆环状。在裂纹转子系统中, 1/2临界转速附近的轴心轨迹随转速发生了规律性的变化,轨迹中存在一个向内凹陷的圆环,其形状和偏置方向均随转速的变化而改变,其中偏置方向在转速变化区间内改变的角度约为π。对比分析图7和图8中的轴心轨迹可知,根据轴心轨迹是否呈规则圆环状、是否出现一个内环,即可对裂纹故障进行简便、清晰的诊断。

(a)ω=0.41ωn(b)ω=0.47ωn(c)ω=0.5ωn(d)ω=0.57ωn
图7 1/2临界转速区无裂纹转子的轴心轨迹
Fig.7 Axis orbits of the uncracked rotor around 1/2 subcritical speed

(a)ω=0.41ωn(b)ω=0.47ωn(c)ω=0.5ωn(d)ω=0.57ωn
图8 1/2临界转速区的轴心轨迹和庞加莱截面图
Fig.8 Axis orbits and poincaré maps around 1/2 subcritical speed
由图9中时域波形图可知,1/2临界转速附近的系统响应均为周期信号,且由于出现次谐波共振现象,在1/2临界转速处系统振动幅值最大,图3中在转速比为0.5处也出现峰值。由图9可知,在频谱图中出现了1X、2X、3X等谐波频率成分,且1X、2X的频率成分具有较大幅值,随着转速的提高,各幅值变化趋势为先增大后减小,当达到1/2临界转速时,各谐波成分的幅值达到最大。
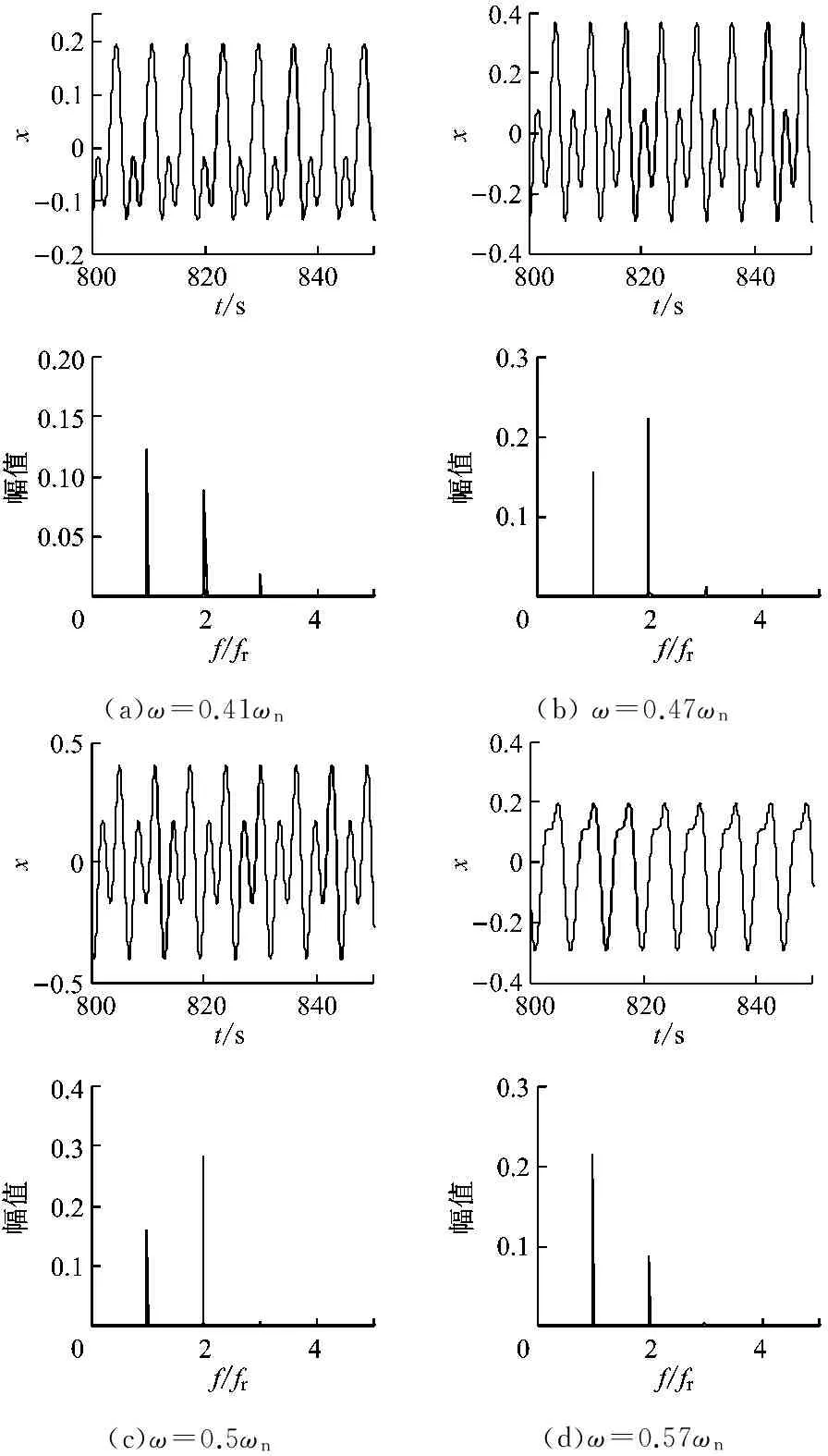
(a)ω=0.41ωn(b)ω=0.47ωn(c)ω=0.5ωn(d)ω=0.57ωn
图9 1/2临界转速区的时域波形和频谱图
Fig.9 Time series and frequency spectra around 1/2 subcritical speed
4 结 论
(1)在1/3临界转速和1/2临界转速附近,裂纹转子系统轴心轨迹的内环形状和偏置方向均发生变化,其中1/3临界转速附近的轴心轨迹存在2个内环,转速区间内偏置方向改变约为π/2。
(2)1/2临界转速附近的轴心轨迹存在一个内环,偏置方向改变约为π。在无裂纹转子系统中,相应的轴心轨迹始终为规则圆环状,其形态在整个转速区间内基本不随转速的变化而改变。因此,根据转子系统在1/3临界转速和1/2临界转速附近的轴心轨迹图是否为规则圆环状、是否存在内环可诊断裂纹故障。
(3)系统随着转速变化未出现分岔现象,一直处于单周期运动,且系统响应中存在分数次共振现象,即在1/n临界转速处系统振动幅值明显增大。后续将在转子实验台做相关实验,对系统轴心轨迹形态进行分析,验证在该参数设定下仿真结果的准确性。
:
[1] 林言丽, 褚福磊, 郝如江. 开斜裂纹转子的动力特性[J].振动与冲击, 2008, 27(1): 25-29.
LIN Yanli, CHU Fulei, HAO Rujiang. Dynamic analysis of a Jeffcott rotor system with an opening slant crack on its shaft[J].JournalofVibrationandShock, 2008, 27(1): 25-29.
[2] 宋光雄, 陈松平, 宋君辉, 等. 汽轮发电机组转子裂纹故障研究及分析[J].动力工程学报, 2012, 32(4): 289-295, 320.
SONG Guangxiong, CHEN Songping, SONG Junhui, et al. Cause analysis of rotor cracks in turbine-generator units[J].JournalofChineseSocietyofPowerEngineering, 2012, 32(4): 289-295, 320.
[3] GUO Chaozhong, YAN Jihong, YANG Weicheng. Crack detection for a Jeffcott rotor with a transverse crack: an experimental investigation[J].MechanicalSystemsandSignalProcessing, 2017, 83: 260-271.
[4] 于涛, 孙伟, 韩清凯. 双裂纹转子系统非线性动力学特性研究[J].振动与冲击, 2013, 32(19): 144-152.
YU Tao, SUN Wei, HAN Qingkai. Nonlinear dynamic behavior of a dual-crack rotor system[J].JournalofVibrationandShock, 2013, 32(19): 144-152.
[5] 唐玉生. 基础—轴承—转子系统损伤故障动力学特性研究[D]. 沈阳: 东北大学, 2013.
[6] 邹剑, 陈进, 董广明. 基于有限元模型单一开裂纹转子的振动分析与无损估计[J].机械工程学报, 2004, 40(7): 29-33.
ZOU Jian, CHEN Jin, DONG Guangming. Vibration analysis and non-destructive evaluation of a rotor with an open crack via finite element model[J].ChineseJournalofMechanicalEngineering, 2004, 40(7): 29-33.
[7] FERJAOUI N, NAIMI S, CHOUCHANE M. Bifurcation analysis of a flexible balanced cracked rotor-bearing system[J].ComptesRendusMécanique, 2016, 344(9): 661-671.
[8] 向玲, 高雪媛, 张力佳, 等. 非线性油膜力下裂纹-碰摩故障转子动力学分析[J].动力工程学报, 2016, 36(10): 788-794.
XIANG Ling, GAO Xueyuan, ZHANG Lijia, et al. Dynamic analysis of a rotor with coupling faults of crack and rub-impact under nonlinear oil-film force[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(10): 788-794.
[9] 陈铁锋. 裂纹转子动力学特性的有限元模拟研究[D]. 上海: 上海交通大学, 2010.
[10] AL-SHUDEIFAT M A, BUTCHER E A. New breathing functions for the transverse breathing crack of the cracked rotor system: approach for critical and subcritical harmonic analysis[J].JournalofSoundandVibration, 2011, 330(3): 526-544.
[11] 刘政, 王建军. 呼吸性裂纹转子的瞬态振动特性分析[J].振动与冲击, 2016, 35(7): 233-240.
LIU Zheng, WANG Jianjun. Analysis on transient vibration characteristics of breathing crack rotor[J].JournalofVibrationandShock, 2016, 35(7): 233-240.
[12] 朱厚军, 赵玫, 王德洋. Jeffcott裂纹转子动力特性的研究[J].振动与冲击, 2001, 20(1): 1-4.
ZHU Houjun, ZHAO Mei, WANG Deyang. A study on the dynamics of a cracked Jeffcott rotor[J].JournalofVibrationandShock, 2001, 20(1): 1-4.
[13] 郑吉兵, 孟光. 考虑非线性涡动时裂纹转子的分叉与混沌特性[J].振动工程学报, 1997, 10(2): 190-197.
ZHENG Jibing, MENG Guang.The nonlinear influences of whirl speed on bifurcation and chaos of a cracked rotor[J].JournalofVibrationEngineering, 1997, 10(2): 190-197.
[14] GASCH R. A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack[J].JournalofSoundandVibration, 1993, 160(2): 313-332.
[15] 刘元峰, 赵玫, 朱厚军. 考虑碰摩的裂纹转子非线性特性研究[J].振动工程学报, 2003, 16(2): 203-206.
LIU Yuanfeng, ZHAO Mei, ZHU Houjun.Nonlinear characteristics of a cracked rotor with rub-impact[J].JournalofVibrationEngineering, 2003, 16(2): 203-206.
