基于Isight和ABAQUS软件的柔轮筒体应力与结构优化

□ 余金宝 □ 范元勋

南京理工大学机械工程学院 南京210094

1 研究背景

谐波齿轮传动技术始于1955年，由美国学者Musser提出，主要应用于航天和机器人等高精密机械传动场合，现在也被应用于某些军事装备和农业器械中。随着航天和机器人技术的飞速发展，对谐波传动体积小、质量轻、承载能力大等性能的要求更高［1］。柔轮作为谐波传动最重要的部件，其体积和强度直接决定着谐波传动的工作情况［2］，因此进行柔轮应力和结构的优化设计，对提高谐波传动的性能有着重要意义。

笔者通过ABAQUS软件进行柔轮负载和空载状态下的应力计算，然后运用Isight软件对柔轮筒体应力和筒长进行优化，以获得既满足强度要求，又能减小体积的最佳结构参数。

2 柔轮筒体的应力计算

2.1 有限元模型的建立

一些对柔轮应力情况影响不大的结构参数可以相应简化或者略去，如齿圈前后端处的倒角、前沿长度及凸台处的螺栓孔等，齿圈部位转换成相应尺寸的齿圈壁厚［3］，齿圈壁厚 δ1的计算式为：

式中：δ为筒体壁厚。

简化后，柔轮的结构如图1所示，图1中的结构尺寸见表1。

▲图1 柔轮结构图

根据表1中的尺寸，建立柔轮的三维模型。柔轮的最大径向变形量为变形因子与模数的乘积，本例中变形因子取1，最大径向变形量为0.5 mm。柔轮和波发生器材料及性能参数见表2。

2.2 边界条件和载荷

在空载条件下，约束柔轮底面所有自由度，将波发生器简化成上下两部分的刚性椭圆环，分别沿径向移动0.5 mm，圆环宽度取13 mm，模拟撑开柔轮的过程。在负载条件下，同样使用空载情况中的边界条件，为了方便柔轮结构的参数化建模，将施加转矩后的刚轮对柔轮的作用力转化为集中力，施加在柔轮齿圈部位［4］，施加边界条件和载荷后的柔轮模型如图2所示。

表1 结构尺寸表mm

表2 材料性能参数

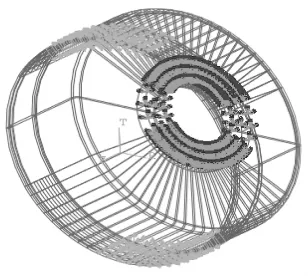
▲图2 载荷和边界条件示意图

2.3 有限元应力结果

运用有限元软件经计算后显示的应力一般是经过处理后的Mises等效应力，它基于von Mises准则，实质就是第四强度理论，Mises应力σ的计算式为：

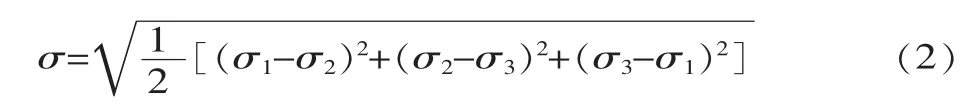
式中：σ1为第一主应力；σ2为第二主应力；σ3为第三主应力。

Mises应力达到材料的屈服极限，零件就会发生屈服破坏。

在ABAQUS软件中，经过以上柔轮和波发生器模型的处理，得到柔轮筒体的空载和负载240 N·m的Mises应力云图，如图3所示。

▲图3 Mises应力云图

由图3可知，柔轮所受应力主要集中在齿圈部位，并且最大应力也发生在此处，分别为399 MPa和437.2 MPa，两者相差不大，但是负载状态较空载状态的柔轮齿圈部位受力复杂，在波发生器长轴方向的齿圈前端受力明显增加。

3 柔轮筒体的优化设计

Isight是一种集成诸多算法的多参数优化设计软件，它提供了有限元软件接口，可以控制CAE（计算机辅助工程）软件的分析计算，并提取相应的计算结果。笔者通过Isight软件调用ABAQUS软件的求解器对柔轮进行应力计算，并根据计算结果进行优化设计，以得到柔轮结构的最佳参数。

3.1 联合优化设计流程

ABAQUS与Isight软件的优化设计流程如图4所示。由图4可知，基于Isight软件的优化设计主要包括Simcode和优化设计两部分。Simcode是一种数据接口，它可以生成试验矩阵并写入和读出相应的数据值，通过执行程序调用ABAQUS软件的求解器分别对不同试验点的有限元模型进行计算，并提取相应的最大应力值，实现柔轮的自动化参数求解，并拟合结构参数与最大应力的近似关系模型。而优化设计是选择合适的数学算法，对之前求出的近似模型进行优化计算，通过设计变量、约束条件及目标函数的设定，得出最优参数［5］。

▲图4 优化设计流程图

3.2 读文件与写文件

Isight软件的读文件和写文件就是在柔轮各结构参数取值范围内选取定量的数据点，再调用ABAQUS软件的求解器进行循环计算和提取结果。

Isight软件利用Python语言进行柔轮的参数化建模并完成最大应力计算和提取［6］。根据短圆柱形柔轮的设计参数，选取的设计变量对应的试验因子a～e及取值范围［7］见表3。

表3 圆柱形柔轮的设计变量及取值范围mm

3.3 试验设计与近似模型

试验设计是优化领域中的重要统计方法，主要包括计划、执行、结果分析三个过程。试验设计有着确定取值范围内数值的最佳组合、分析输入与输出参数之间的关系和变化规律、构建近似模型及经验公式等作用。

Isight软件包含多种试验设计方法，根据柔轮结构的复杂性，本次试验选用最优拉丁超立方（Optimal Latin Hypercube）设计方法，根据设计变量可知试验因子有5个、取样点200个。

近似模型就是根据试样点用近似关系拟合输入输出变量之间的关系，当精度足够高时，可信度满足，可以用函数关系代替ABAQUS软件的求解过程，节省时间成本，提高优化设计效率［8］。近似模型的关系拟合函数f（x）式为：式中：（x）为描述响应近似值的多项式；ε 为（x）与f（x）的误差，服从正态分布。

优化设计的近似模型选用响应面模型，它可以通过较少的样点拟合出误差较小的近似函数［9］，有很强的实用性和广泛性，其一般表达式为：

式中：x为拟合变量；n为变量个数；y为用函数描述的响应值；ci为多项式常数；φi（x）为基函数；k为基函数的个数。

在Isight软件的结构优化和分析中，采用二阶多项式，即二阶响应面模型，其表达式为：

常数矩阵为H=（c0，c1，...，ck）T，可以用最小二乘法确定其值，具体为：

式中：Y=（y1，y2，...，yn）T为实际响应值矩阵；X为基函数矩阵；z为试验次数。

将200个试样点经响应面模型拟合后的误差见表4。由表4可知，响应面模型的最大响应误差、平均相对误差及均方根误差都很小，与应力实际值相差七个量级，可忽略不计，而且决定因数较高，都大于0.95，所以用响应面模型代替ABAQUS软件的求解过程是合理的。

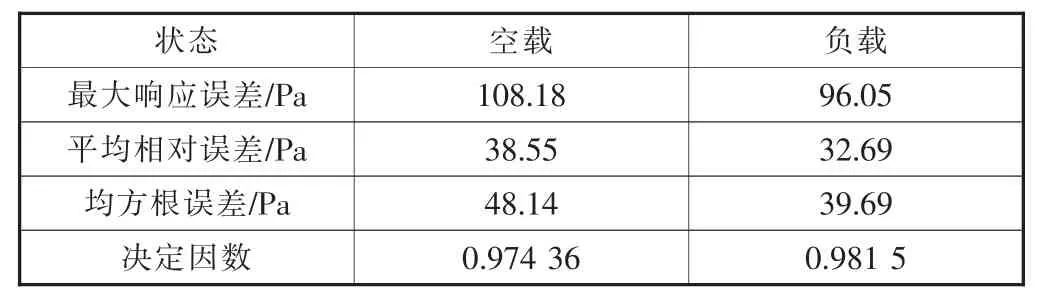
表4 拟合误差值

3.4 优化数学模型及算法

在保证柔轮内径不变的条件下，通过改变柔轮的结构参数，使应力或者筒长达到最小值，属于多目标优化设计。

Isight软件含有多种优化设计算法，笔者选择基于遗传算法开发的NSGA-II多目标优化算法对柔轮进行优化设计，遗传算法流程如图5所示。

▲图5 遗传算法流程图

NSGA-II优化算法具有较优的探索能力，它先通过“拥挤距离”的方法进行个体排序。然后根据父代群体的交叉和变异获得子代群体，合并父子群体。最后按照Pareto优化关系，将个体与目标向量比较，并分为多个顺序控制的前沿层，评价个体的优劣，选出最佳值［10-11］。

3.5 优化结果及对比分析

内径一定，在保证柔轮筒体长度不变的条件下，通过Isight软件优化设计得到的优化值与初值见表5。

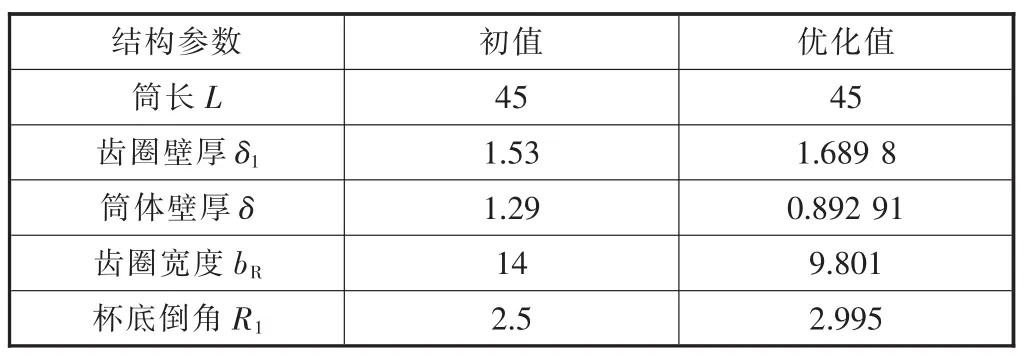
表5 优化筒长优化值与初值参数对比表mm

根据优化值得到的柔轮优化后应力云图如图6所示，由图6可知，优化后的柔轮在空载和负载状态下的最大应力为351.3 MPa和365.5 MPa，与初值相比分别下降了12%和16%，受力情况明显改善。

▲图6 优化后应力云图

在Isight软件优化计算中，也可以将柔轮筒长最小作为设计目标，以减小其质量和体积。由于是多目标优化，负载应力较空载应力大，所以将负载应力和筒长最小作为优化目标，在Isight软件中可以在迭代图中选出不同柔轮长度下对应的应力值，在保证柔轮最大应力基本不变的情况下，得到筒体最小优化值及初值，见表6。

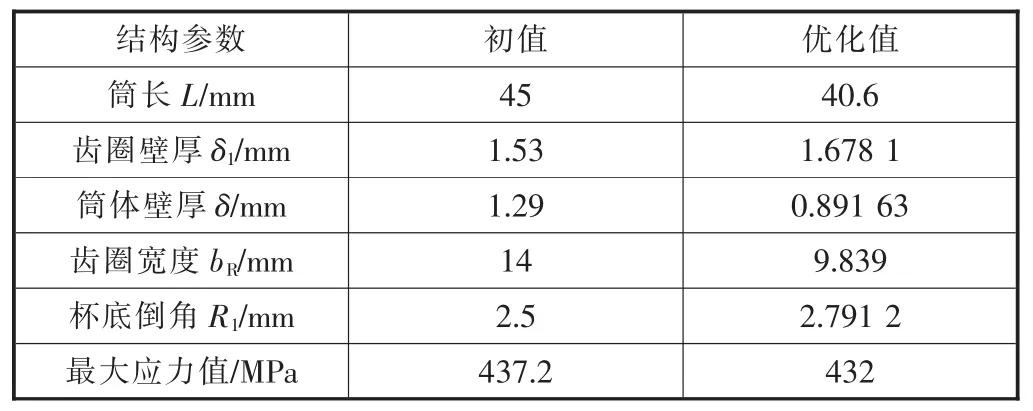
表6 优化筒长和应力优化值与初值参数对比表

由表6可知，在保证柔轮整体受力基本不变的情况下，优化后的最小筒长为40.6 mm，降低了约10%，节约了材料成本并减小了柔轮体积。

4 结论

运用ABAQUS软件进行柔轮筒体的应力分析，得出了空载和负载条件下的最大应力值，两者都发生在与波发生器相接触的柔轮齿圈部位，为柔轮筒体应力的优化设计提供了方向。

运用Isight软件进行柔轮筒体结构的优化设计，在保证筒长不变的条件下，改变其余结构参数，使空载、负载应力分别下降了12%和16%，增加了柔轮的工作寿命；同时在保证柔轮最大应力不增加的情况下，使筒体长度最高下降了10%，减小了柔轮的体积和质量，达到轻量化设计的目的。